基于极大值原理的电动车组节能操纵
梁志成,王青元,何 坤,冯晓云
(西南交通大学 电气工程学院,四川 成都 610031)
列车节能操纵是在保证列车安全、准点、舒适、精确停车的基础上,通过优化列车工况序列,使列车运行能耗最小。列车时刻表规定的区间运行时间通常大于最大能力运行时间,因此可利用富余时间和线路纵断面进行节能优化。国内外学者已对此进行了大量的研究[1-6],得出列车最优工况序列由全力牵引、恒速控制、惰行和全力制动所构成。文献[4]用变分法证明了区间不存在大坡道时,相邻恒速区段之间只存在单个大坡道时最优工况切换的存在性和唯一性,但其分析未考虑线路限速的影响。文献[6]应用极大值原理,推导出考虑再生制动能量利用时列车最优工况的切换原则,并给出了求解算法,但对线路限速约束影响下工况切换的讨论较为粗糙。文献[7]为解决模型奇异性导致列车工况切换点无法完全确定的问题,引入优秀司机操纵经验,用启发式算法寻找工况切换点,取得了较好的节能效果,但该方法未对工况切换点的最优性进行验证,且耗时较长,难以应用于列车节能运行模式曲线的在线计算。
本文以电动车组列车(以下简称列车)牵引能耗最小为优化目标,考虑线路限速,应用极大值原理推导节能操纵的最优运行工况集,通过分析伴随变量的变化规律,挖掘列车节能操纵的解析属性,在此基础上给出一种求解列车最优工况序列的数值算法,为列车自动驾驶或辅助驾驶系统在线生成节能最优模式曲线提供帮助。
1 列车运行控制的数学模型
1.1 模型假设
为便于对列车运行过程进行分析,对列车模型做如下假设:
(1)不考虑列车使用电制动工况时的再生反馈能量利用。基于电动车组按照减速度-速度特性施加制动力的特点,将列车的电制动和空气制动特性归并到同一制动特性曲线下,得到综合制动特性曲线,且不考虑空气制动的充风时间和缓解时间。
(2)列车的牵引力和制动力是连续的,可取特性包络线下对应车速的任意点力的值,即μt和μb在其取值范围内连续,列车可实现恒速运行。
(3)由于列车正常运行情况下一般不会使用紧急制动工况,因此本文中的列车制动工况只限于常用制动工况。
(4)列车辅助系统,如照明、空调和风机等产生的能耗只与运行时间有关,与列车运行工况无关。
1.2 模型描述
列车在具有坡道和曲线的轨道上行驶,计算其运动状态时需要考虑车长的影响,因此单质点模型不再适用。本文对单节列车采用“均质棒”模型,认为单节动车和单节拖车均按其长度均匀分配质量。列车的加算坡道附加阻力根据列车在不同线路条件下的长度分布进行加权平均计算得到。
由牛顿第二定律,列车运行的数学模型可描述为
( 1 )
( 2 )
式中:v为列车速度,m/s;x为列车在线路上所处的位置,m;t为时间变量,s;ft(v)、bb(v)、w0(v)分别为考虑回转质量后列车在车速v下的最大单位牵引力、最大单位综合制动力以及单位基本运行阻力;控制量μt、μb由列车牵引级位、常用制动级位折算得到;g(x)为考虑回转质量后列车在位置x的单位加算坡道附加阻力。
为便于分析,将列车速度v和运行时间t表示为以列车位置x为自变量的函数,即v(x)和t(x),由式( 1 )和式( 2 ),得到微分方程
( 3 )
( 4 )
由于列车施加的牵引力和综合制动力不能超过其最大值,因此控制变量应满足约束
0≤μt≤1
( 5 )
0≤μb≤1
( 6 )
假设列车运行区间的长度为S,时刻表给定的区间运行时间为T,则列车从区间起点启动运行,经过T时间到达区间终点并停车,可以表示为
v(0)=0,v(S)=0
( 7 )
t(S)-t(0)=T
( 8 )
考虑到列车运行的安全性,列车车速不能超过其所在位置的线路限速,且列车应能在任意车速下制动减速,因而满足
v(x)≤V(x)
( 9 )
bb(v)+w0(v)+g(x)>0
(10)
优化目标是使列车区间运行的牵引能耗最小,即
(11)
式中:ηt为列车牵引工况下传动系统的机电效率。
2 节能最优运行工况及其切换
2.1 节能最优运行工况分析
根据庞特里亚金极大值原理,结合状态方程( 3 )和方程( 4 ),构造哈密顿函数[8]
(12)
式中伴随变量λ1、λ2应满足
(13)
λ1(0)自由,λ1(S)自由。
(14)
λ2(0)自由,λ2(S)自由。M(x)为考虑约束条件( 9 )而引入的单调非减有界变差函数[9],其满足

(15)
dM(x)≥0
(16)

(17)
即在列车运行全过程中,λ1恒为常数。
式(12)可进一步简化为
(18)

表1 伴随变量不同取值对应的列车最优运行工况

(19)

(20)
联立式(19)和式(20),可得
(21)
可简化为
(22)
下面分别对θ=1和θ=0两种情形展开分析。
(1)当θ=1且保持不变时,由表1可知μt∈[0,1],μb=0,即列车保持部分牵引工况运行,此时有
(23)
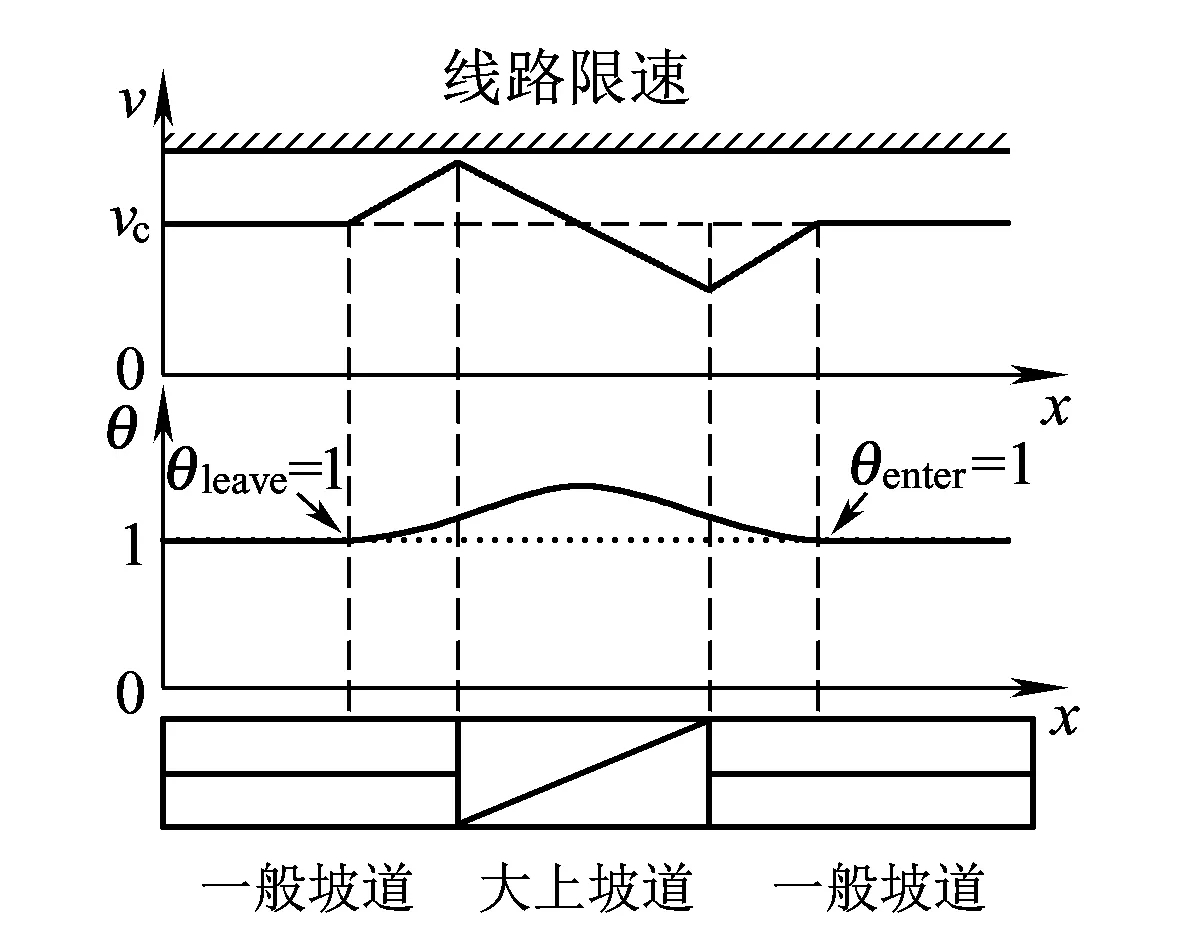
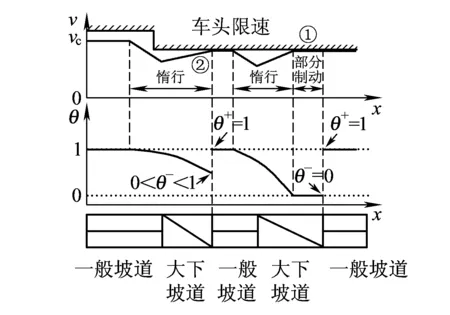
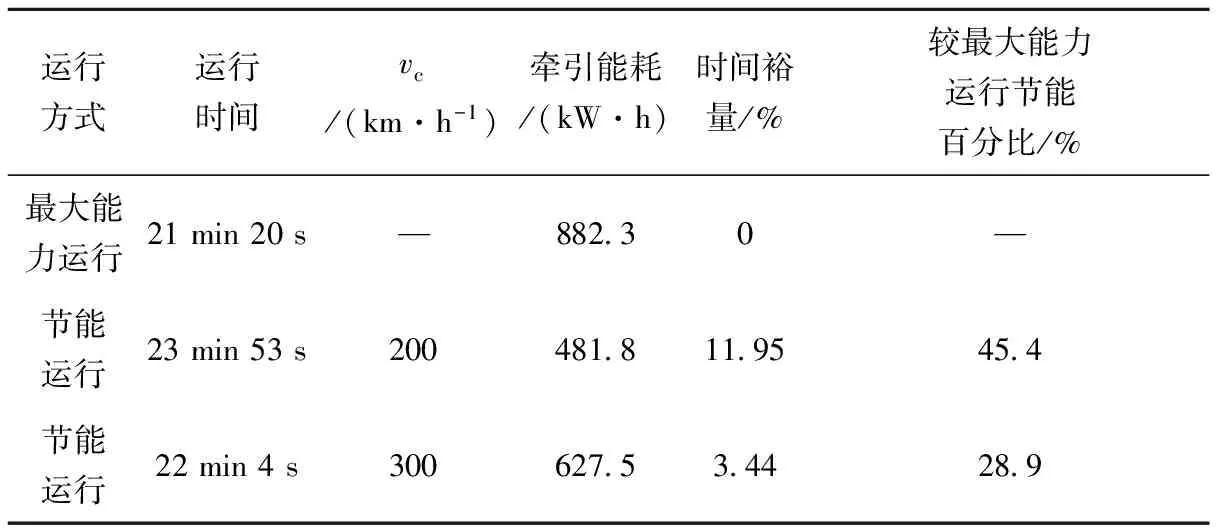
当v(x) (24) (25) 当v(x)=V(x)时,有dM(x)≥0,列车以线路限速恒速运行。由ψ(v)的单调性可知,为使V(x)为方程(23)的解,需满足vc≥V(x)。 因此,对于最优运行工况而言,列车部分牵引工况只有在速度保持阶段才使用。当vc≤V(x)时,列车使用部分牵引工况保持车速vc;当vc>V(x)时,列车由于线路限速的限制无法达到速度vc,可使用部分牵引工况保持车速为V(x)。使用部分牵引工况的目的是实现列车恒速运行,其与实际电动车组的牵引恒速控制模式相对应。此时列车牵引力视总的列车运行阻力大小而定,因而控制量取值满足μt∈[0,1]。 (2)当θ=0且保持不变时,由表1可知μt=0,μb∈[0,1],即列车保持部分制动工况运行,此时有 (26) 由λ1<0得 dM(x)>0 (27) v(x)=V(x) (28) 因此,对于最优运行工况而言,列车使用部分制动工况只适用于为避免下坡道运行时车速超过线路限速,通过施加一定的制动力将车速保持在线路限速V(x)的情形,与实际电动车组的制动恒速控制模式相对应。此时列车制动力视实际受力情况而定,因而控制量取值满足μb∈[0,1]。 在分析伴随变量θ位于不同取值区间对应的最优运行工况的基础上,对θ的动态特性展开分析,得到最优运行工况的切换原则。 (1)当θ>1且vc (29) (2)当0<θ<1,v(x) (30) 列车的节能最优工况序列由最优运行工况集合(即全力牵引、部分牵引/牵引恒速、惰行、部分制动/制动恒速、全力制动)中的工况组合连接而成。在列车运行全过程中,λ1恒为常数,由式(25)的分析可知,vc一旦给定,即可求出λ1并将其代入微分方程(22)以求解伴随变量随列车运行的数值变化,再根据表1确定列车的最优控制工况及其切换时机。下面给出一种给定vc条件下节能最优工况序列的求解过程。 为保证整列车均不超过线路限速,即列车通过低限速区段以其尾部也通过该区段为标志,考虑列车车长的影响,将原线路限速转换成列车车头位于线路不同位置时对应的线路限速V(x)。 由前述的“均质棒”模型,计算列车在整个运行区间的单位加算坡道附加阻力变化曲线g(x),其中x为列车车头位置。 列车在线路上行驶时,纵断面和线路限速的组合构成了复杂多变的运行条件。但从列车节能操纵的角度,线路可看成是由若干个有着各自目标运行速度的坡道区段所组成。其中坡道区段的目标运行速度取值为vc与当前坡道区段线路限速V(x)的较小值。当列车在线路的某个坡道区段运行时,根据其在目标运行速度的恒速保持能力,可将该坡道区段分为一般坡道区段、大上坡道区段和大下坡道区段三种坡道类型。设列车在该坡道区段的目标运行速度为vtarget,结合式( 1 ),上述三种坡道类型的具体定义为 (1)一般坡道区段是指列车使用牵引或惰行工况可以保持目标运行速度的坡道区段,满足 μtft(vtarget)-w0(vtarget)-g(x)=0 μt∈[0,1] (31) (2)大上坡道区段是指列车在目标运行速度下使用全力牵引工况车速仍然降低的坡道区段,满足 ft(vtarget)-w0(vtarget)-g(x)<0 (32) (3)大下坡道区段是指列车在目标运行速度下使用惰行工况车速仍然上升的坡道区段,满足 -w0(vtarget)-g(x)>0 (33) 根据此定义,将给定列车运行区间划分为若干个坡道区段,划分时遵循每个坡道区段内坡道类型唯一且只有一个线路限速值的原则,如图1所示。 图1 坡道区段的划分 本文将恒速段定义为列车在应用最优控制工况条件下保持恒定车速的运行区域。列车保持恒定车速的情形有两种: (1)列车使用牵引恒速控制工况保持车速为vc或线路限速V(x),满足θ=1; (2)列车使用制动恒速控制工况保持车速为线路限速V(x),满足θ=0。 因此,将恒速段分为牵引恒速段和制动恒速段两种。牵引恒速段是含单一目标运行速度的一般坡道;制动恒速段是受到线路限速影响的大下坡道,其目标运行速度只有一个。当vc的值改变时,线路上坡道的类型可能发生改变,进而影响恒速段的划分。列车运行区间的起点和终点都定义为限速为0的单点恒速段。 计算列车节能最优速度模式曲线时,以恒速段为基准,将非恒速段看作是恒速段的过渡连接,最终将包括区间起点与终点在内的若干个恒速段连接起来,并达到准点运行的要求。对于存在最优连接曲线的两个恒速段而言,沿列车运行方向,把与最优连接曲线起点相连的恒速段称为前恒速段,该点为恒速段的离开点,把与最优连接曲线终点相连的恒速段称为后恒速段,该点为恒速段的进入点。显然,恒速段的离开点应在进入点之后,或者与进入点重合,否则视为无效连接,特别地,区间起点只有离开点,区间终点只有进入点。 由极大值原理可知,当系统状态不受约束时,伴随变量连续。因此,当最优连接曲线未触及线路限速时,恒速段的进入点和离开点处都要满足伴随变量θ连续,用θleave表示前恒速段离开点处θ的取值,用θenter表示后恒速段进入点处θ的取值。 (1)θ连续变化情况下的连接方法 假设待连接的两恒速段均为牵引恒速段,由于列车在牵引恒速段的必要条件是θ=1,因此应满足θleave=1和θenter=1。 若两恒速段之间仅存在单个大上坡道区段,根据最优工况集和θ的变化规律,列车应在大上坡道区段前的某一位置切换到全力牵引工况,使车速v上升,θ增大,进入大上坡道区段后,车速v下降,此时要想θ再次减小到1,车速v必须下降到vc以下,离开大上坡道区段后,车速v重新上升,θ继续减小,当车速v上升至vc时,恰好满足θ=1,列车切换到部分牵引工况保持恒速,如图2所示。 图2 内含单个大上坡道区段的两恒速段最优连接示意图 若两恒速段之间仅存在单个大下坡道区段,列车应在大下坡道区段前某一位置切换到惰行工况,使车速v下降,θ减小,进入大下坡道区段后,车速v上升,此时要想θ再次增大到1,车速v必须上升到vc以上。离开大下坡道区段后,车速v重新下降,θ继续增大,当车速v下降至vc时,恰好有θ=1,列车切换到部分牵引工况保持恒速,如图3所示。 图3 内含单个大下坡道区段的两恒速段最优连接示意图 若两恒速段之间存在由大上坡和大下坡组成的组合大坡道区段,应根据第一个大坡道的类型判断列车应使用的工况。若为大上坡,则列车应在大坡道区段之前切换到全力牵引工况;若为大下坡,则列车应在大坡道区段之前切换到惰行工况。其后列车工况根据θ取值变化在表1选取。当列车离开大坡道区段且车速与后恒速段的速度相等时,应恰好有θ=1,列车切换到牵引恒速工况,如图4所示。 图4 内含大上坡和大下坡的两恒速段最优连接示意图 (2)θ发生跳变情况下的连接方法 由式(15)和式(16)可知,当列车车速等于其所在位置的线路限速即v(x)=V(x)时,dM(x)≥0,且在列车车速进入或离开线路限速约束时,伴随变量θ可能发生由dM(x)引起的正跳变[9]。由于θ跳变只能在线路约束处发生,为便于计算,可结合坡道区段的划分结果,预先确定θ可能发生跳变的位置,将其定义为若干个θ跳变点,从而将最优速度曲线的连接分解为恒速段之间的连接、恒速段与θ跳变点的连接以及θ跳变点之间的连接3个子任务。一般来说,θ跳变点出现在大上坡的起点限速处、大下坡的终点限速处、低速恒速段的起点和终点以及区间的起点和终点。对于区间起点和终点而言,对应的边界条件( 7 )等同于线路限速为0,因此将区间起点和终点视为θ跳变点,以纳入到统一的连接理论框架进行分析。 由于θ的跳变量必须为正,若θ跳变前的取值已知,即可确定θ跳变后可能的取值范围,从而为搜索最优工况切换点提供依据。设θ跳变前的值为θ-,跳变后的值为θ+,下面对θ发生跳变的不同情况分别进行分析。 ①θ-=1,θ+>1 当列车从目标运行速度较低的恒速段使用全力牵引工况向目标运行速度较高的恒速段过渡时,θ跳变点为低速恒速段的末端,如图5中①所示。 图5 全力牵引连接示意图 当列车在目标运行速度与线路限速相等的恒速段运行但前方出现大上坡,需要使用全力牵引工况过渡时,为保证不超限速,全力牵引工况应在此大上坡的起点施加,该点为θ跳变点,如图5中②所示。 ②θ->1,θ+>θ->1 连接两个恒速段时,当在假设θ连续变化条件下得到的最优连接曲线存在因使用全力牵引工况通过大上坡而导致列车速度超过线路限速的情况时,应重新调整工况切换点位置,使列车车速在大上坡的起点处恰好等于线路限速,以免超速,此时θ跳变点为该大上坡的起点限速处,如图6所示。 图6 全力牵引连接示意图 ③θ-<1,θ+=1 制动恒速段位于线路限速影响的大下坡道区段,存在使用部分制动工况以防超速的可能性。部分制动工况可从惰行工况切换得到,必要条件为θ连续下降到0,如图7中①所示。若列车惰行运行至制动恒速段的终点时仍有θ>0,即未满足使用部分制动工况的条件,为避免列车超速行驶,求解工况切换点时应使列车在大下坡道区段终点处的车速恰好等于线路限速,θ在该点发生正跳变,列车切换至其他工况(如部分牵引)运行,如图7中②所示。 图7 大下坡道区段的惰行连接示意图 ④θ-<0,θ+=0 部分制动工况可从全力制动工况切换得到。当列车使用全力制动工况运行至制动恒速段的起点时,车速恰好等于该恒速段的目标运行速度,则θ在该点发生跳变,列车切换至部分制动工况运行,如图8所示。 图8 全力制动连接示意图 求解最优连接时,通过四阶Runge-Kutta法联合求解式( 3 )和式(22),根据θ的取值切换列车工况,从而得到列车速度v和θ随列车位置的变化。 对于恒速段之间的连接,由于θ是连续的,将列车工况切换点位置作为迭代变量,采用二分法搜索在一定误差限下满足恒速段进入点和离开点最优化条件的工况切换点。若能找到,则检查连接曲线是否超过线路限速。如果没有超过限速,则将其视为两恒速段的最优连接,反之应插入θ跳变点,重新搜索最优工况切换点。 对于涉及θ跳变点的连接,虽然θ的跳变量大小一般不能预先确定,但可将θ的跳变量为正作为验证连接曲线正确性的判断标准。例如,连接恒速段与θ跳变点时,连接曲线与恒速段相交处θ的取值应满足相应的最优化条件,且θ在跳变点的跳变量为正值;连接两个θ跳变点时,应满足θ在这两个跳变点的跳变量均为正值,鉴于跳变点的速度和位置已经确定,可将后一跳变点θ跳变前的取值作为迭代变量,以“反算”的方式计算连接曲线,采用二分法搜索最优连接。若无法找到满足θ跳变条件的解,则说明给定的两个连接对象之间不存在最优连接。 由前述分析可知,vc的取值决定了坡道区段的划分及其相互连接关系,从而决定列车的区间运行时间。本文的列车节能操纵优化模型中,vc是用来控制区间运行时间的参数,而不是表征区间平均运行速度的量。对于同一运行区间而言,vc的值越大,计算所得的节能速度模式曲线对应的区间运行时间越短。随着vc的不断增大,区间运行时间逐渐向最大能力运行时间逼近,vc的取值可以超过区间最高线路限速甚至列车本身的构造速度;通过合理调整vc的取值,可以实现区间准点运行。因此,在最终生成的速度模式曲线中,车速有可能无法达到vc对应的速度。 节能准点寻优算法的目标是确定一条可将区间起点和终点有效连接起来的最优运行曲线,并满足准点性要求。具体步骤如下: 步骤1:计算列车在给定优化区间最大能力运行时的速度曲线及其对应的最短运行时间Tmin。若给定区间运行时间Ttarget大于Tmin,则执行步骤2,否则返回最大能力运行工况序列,优化终止。 步骤2:设定vc的值,并计算λ1的值,然后根据vc划分坡道区段,定义恒速段和θ跳变点,为避免不必要的连接计算量,首先移除最大能力运行速度曲线无法到达的恒速段和θ跳变点,然后按照位置排序得到由恒速段和θ跳变点构成的有序集合U={Ci},i=1,…,n,其中Ci表示第i个待连接元素,C1为区间起点,Cn为区间终点。为提高寻优效率和便于编程实现,采用递归搜索算法。 步骤3:连接集合U的元素,并在连接成功后保存最优工况序列。连接两个元素时,用p表示前元素的序号,用q表示后元素的序号。 步骤3.1:若i 步骤3.3:若q=n,则找出在Cp之前且与Cp直接相连的元素Cm(1≤m 步骤4:根据步骤3中所生成的列车工况序列,对列车区间运行进行仿真,计算区间运行时间T。 步骤5:若|T-Ttarget|<3 s,则认为列车已满足准点性要求,优化结束。否则,若T>Ttarget,则提高vc,重复步骤2;若T 以CRH2型4M4T动车组为原型,建立仿真列车模型,相关参数见表2。为充分验证本文提出的列车节能速度曲线求解算法的正确性和有效性,并体现多种线路坡道和限速组合下的最优工况切换原则,仿真运行线路的纵断面和限速数据是在符合动车组运用条件的前提下通过合理假设而得到的。对于坡道较平缓的实际线路,本文的寻优算法同样适用。仿真线路全长60 km,限速数据见表3,纵断面数据见表4。 表2 仿真用列车参数 表3 线路限速 表4 线路纵断面 经仿真,列车在给定区间的最大能力运行时间为Tmin=21 min 20 s。当给定大于该时间的区间运行时间时,应用所提出的区间最优连接搜索算法,通过调整vc以达到准点运行要求。为对比不同区间运行时间下(对应不同的vc)的节能最优运行曲线,给定两个区间运行时间T1=23 min 53 s和T2=22 min 4 s分别进行仿真,得到对应的节能最优运行模式曲线如图9和图10所示,两种情况下的vc取值和能耗数据见表5。 图9 区间运行时间为23 min 53 s对应的节能速度模式曲线 图10 区间运行时间为22 min 4 s对应的节能速度模式曲线 运行方式运行时间vc/(km·h-1)牵引能耗/(kW·h)时间裕量/%较最大能力运行节能百分比/%最大能力运行21min20s—882 30—节能运行23min53s200481 811 9545 4节能运行22min4s300627 53 4428 9 图9中,满足准点要求时vc=200 km/h。列车使用全力牵引从目标运行速度较低的恒速段向目标运行速度较高的恒速段运行(包括起动阶段),如a~b段、d~e段、k~l段;列车使用部分牵引以vc或小于vc的线路限速值为目标速度恒速运行,如c~d段、f~g段、j~k段、l~m段、p~q段、r~s段;列车在恒速运行过程中前方遇到单个大坡道或由大上坡和大下坡构成的组合坡道时,使用全力牵引和惰行进行恒速段连接,当连接受到线路限速影响时,使用全力牵引g~h段和i~j段,以及惰行h~i段;当连接不受线路限速影响时,使用全力牵引m~n段和o~p段,以及惰行n~o段;当列车调速过程中遇到大下坡时,为避免超速,若尚未达到使用部分制动的条件,列车将使用惰行直至大下坡的终点,如b~c段、e~f段、h~i段、q~r段;当列车从目标运行速度较高的恒速段向目标运行速度较低的恒速段运行(包括进站停车)时,若尚未达到使用全力制动的条件,则使用惰行进行连接,如q~r段,若达到使用全力制动的条件,则使用惰行(如s~t段)和全力制动(如t~u段)进行连接。 图10中,由于设定区间运行时间的缩短,满足准点要求时vc=300 km/h,vc大于区间所有线路限速,此时列车牵引恒速运行均以其所处位置的线路限速为目标速度,如d~e段、g~h段、k~l段、o~p段、s~t段;当列车从目标运行速度较低的恒速段向目标运行速度较高的恒速段运行且遇到大下坡时,与图9相比,vc的提高使全力牵引工况(如a~b段、e~f段)增加,惰行工况(如b~c段、f~g段)减少,在大下坡道区段出现了部分制动工况(c~d段);由于vc的提高,图9中恒速段l~m段消失,又由于受到线路限速的影响,使用全力牵引l~m段和n~o段,以及使用惰行m~n段;当列车从目标运行速度为220 km/h的恒速段向目标运行速度为150 km/h的恒速段调速时,因vc的提高而达到了使用全力制动的条件,出现了全力制动工况(q~r段)和在整个大下坡道区段使用的部分制动工况(r~s段);在列车进站停车的过程中,vc的提高使惰行工况减少(图9的s~t段),全力制动工况增加(图9的t~u段),并且出现了全力牵引工况(图10的t~u段)。 列车最大能力运行时的工况序列可通过不断提高vc的取值来逼近得到,本例中当vc>1 000 km/h时,区间运行时间与最大能力运行时间相差小于1 s,可近似为最大能力运行。从表5的仿真结果数据来看,与列车最大能力运行相比较,在满足准点的前提下,当设定11.95%的运行时间裕量时,最多可节省45.4%的牵引能耗;当设定3.44%的时间裕量时,最多可节省28.9%的牵引能耗。因此,通过合理设置列车区间时分裕量,可以取得可观的节能效益。 仿真在主频为1.9 GHz、内存为2 G的计算机上进行。当给定区间运行时间后,求解满足准点要求的节能速度模式曲线耗时约5 s,说明所提出的算法能满足电动车组在线计算节能最优模式曲线的要求。 (1)以列车牵引能耗最小为优化目标,考虑线路限速,基于极大值原理的最优化条件,得到最优运行工况集,以及伴随变量连续和发生跳变条件下最优运行工况的切换原则,并对多种限速和坡道组合下的节能优化操纵进行了分析。 (2)在理论分析的基础上,提出一种求解列车最优工况序列的数值算法,并通过仿真验证了该算法的正确性和有效性。从仿真运行结果来看,该算法耗时较短,克服了以往寻优算法因耗时较长只能进行离线优化的缺点。同时,最大能力运行方式可看作是定时节能优化操纵的一种特殊情况,可通过提高vc的取值来逼近。 (3)本文探讨了区间运行定时约束下列车节能最优模式曲线的求解方法,对列车自动驾驶或辅助驾驶系统的模式曲线优化和在线调整具有一定的借鉴意义。列车在实际运行过程中会受到过电分相、信号变化等因素的影响,对于如何求解此类因素约束下的节能优化操纵问题,需要进一步的研究。 参考文献: [1]LEE D H,MILROY I P,TYLER R L.Application of Pontryagin’s Principle to the Semi-automatic Control of Rail Vehicle[C]//Proceedings of the Second Conference on Railway Engineering,1982:233-236. [2]BENJAMIN B R,LONG A M,MILROY I P,et al.Control of Railway Vehicles for Energy Conservation and Improved Timekeeping[C]//Proceedings of the Conference on Railway Engineering,1987:41-47. [3]LIU R F,IAKOV M G.Energy-efficient Operation of Rail Vehicles[J].Transportation Research.Part A:Policy and Practice,2003,37(10):917-932. [4]XUAN V.Analysis of Conditions for the Optimal Control of a Train[D].University of South Australia,2006. [5]HOWLETT P G,PUDNEY P J,XUAN V.Local Energy Minimization in Optimal Train Control[J].Automatica,2009,45(11):2692-2698. [6]KHMELNITSKY E.On an Optimal Control Problem of Train Operation[J].IEEE Transactions on Automatic Control,2000,45(7):1257-1266. [7]朱金陵,李会超,王青元,等.列车节能控制的优化分析[J].中国铁道科学,2008,29(2):104-108. ZHU Jin-ling,LI Hui-chao,WANG Qing-yuan,et al.Optimization Analysis on the Energy Saving Control for Trains[J].China Railway Science,2008,29(2):104-108. [8]解学书.最优控制理论与应用[M].北京:清华大学出版社,1986. [9]RICHARD F H,SURESH PS,RAYMOND G V.A Survey of the Maximum Principles for Optimal Control Problems with State Constraints[J].SIAM Review,1995,37(2):181-218.
2.2 节能最优运行工况的切换原则
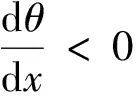






3 节能最优工况序列求解算法
3.1 划分坡道区段

3.2 恒速段的定义
3.3 恒速段连接





3.4 局部最优连接搜索算法
3.5 准点调整
3.6 区间最优连接搜索算法


4 仿真验证





5 结束语

