深空探测着陆器着陆冲击动力学相似技术研究

陈金宝， 万峻麟， 成 玫， 聂 宏

(1.南京航空航天大学航天学院， 江苏 南京 210016； 2.中国电子科技集团公司第二十八研究所， 江苏 南京 210018； 3.上海卫星工程研究所， 上海 201100； 4.南京航空航天大学航空宇航学院， 江苏 南京 210016)

深空探测着陆器着陆冲击动力学相似技术研究

陈金宝1， 万峻麟2， 成 玫3， 聂 宏4

(1.南京航空航天大学航天学院， 江苏 南京 210016； 2.中国电子科技集团公司第二十八研究所， 江苏 南京 210018； 3.上海卫星工程研究所， 上海 201100； 4.南京航空航天大学航空宇航学院， 江苏 南京 210016)

针对未来目标天体表面低重力场模拟，推导了探测器软着陆动力学相似性关系，提出了一种通过改变探测器着陆初始条件，并对试验数据进行后续处理来模拟目标天体表面低重力场的新方法，通过算例验证了该方法对于不同的探测器状态及土壤状态均具有广泛的适应性。通过该方法进行探测器的相关低重力场模拟试验，可以使用探测器原型且试验设备简单、操纵容易，具有很强的实用性，方便进行探测器主要参数的优化设计，该方法可用于后期月球探测、火星探测及其他地外天体低重力模拟试验中。

着陆器； 着陆冲击； 低重力模拟； 相似

引 言

以月球、火星、小行星探测为主的深空探测计划将根据任务需求对深空探测着陆器任务的研制提出了高性能、高可靠、长寿命等较高的指标要求。以月球探测为例，由于月球表面存在着表面特殊着陆地形、重力场、土壤环境等因素，月球探测器的月面软着陆过程将受到一定程度的影响。因此，与航空飞机起落架等常规地面着陆冲击试验相比，月球探测器地面着陆冲击试验还需要另外增加月面地形模拟、月壤性能模拟和月球重力场模拟等特殊装置。在上述问题中，如何有效的建立月球重力场是近年来研究的热门领域。目前，国内外已有报道或介绍的模拟月球重力场的着陆试验装置或模拟方法有：滑轮平衡法[1-2]、反推火箭法、斜坡法[3]、气球浮力法[4]、气腔模拟法[5-6]、全机1/6模型法[7]、降落伞法[8-9]、电磁阻力法[10]、计算机仿真法[11]。其中，试验中较常用的月球重力场模拟装置和方法为：滑轮平衡法、斜坡法、气腔模拟法和全机1/6模型法。

上述常规低重力模拟方案存在着误差大，对试验设备和技术手段要求高，试验适应能力差等缺点。尽管中国“嫦娥”探月工程已开展10余年，但是针对着陆器低重力模拟试验却没有很好解决，依然保守地采用常规地球重力下验证试验。采用常规地球重力代替月面低重力对着陆器进行设计及试验虽然可保证着陆器在月球表面成功着陆，但显然结果偏保守，而国外基于缩比模型对大型着陆器进行低重力状态着陆冲击性能试验已早以应用。目前，由于中国短时期内深空探测着陆器以中小型探测器为主，其内部多由薄板及桁架组成，限于制造工艺等因素，却不能直接采用对原样机模型进行直接缩比方式。因此针对深空探测着陆器低重力模拟领域研究，寻找工程易实现且经济可行的着陆器试验方案是非常有必要的。鉴于此，本论文研究一种通过改变探测器着陆初始着陆条件，并对试验数据进行后续处理来模拟地外天体重力场的方法，通过该方法进行探测器模拟目标天体表面低重力试验，可以使用探测器原型样机且试验设备简单、操纵容易，经过算例验证该方法具有广泛的适应性，方便进行探测器主要参数优化设计。

1 深空探测着陆器着陆冲击试验相似性分析

1.1 深空探测着陆器的几何相似性分析

对于深空探测着陆器原型与其任意比例的模型而言，其所占据的空间对于尺寸之比是一个常数，那么二者存在几何相似关系。令几何相似常数写为

(1)

式中c表示相似常数(通常选定为某已知数值)，l表示长度物理量，L表示探测器所有方向的线性尺寸，下标p表示原型，m表示模型。

为了方便描述探测器模型的尺寸，论文将所有相似常数均定义为探测器模型的物理量与探测器原型的物理量之比。几何相似是单值条件，也是最基本的相似条件，否则探测器原型与模型间就不具备相同的研究现象，论文以月球着陆器为例进行分析。

1.2 基于牛顿定律确定月球着陆器的相似常数

月球着陆器原型和模型之间是几何相似的，那么如果它们的系统中对应点的力方向一致且互成比例，则认为该月球着陆器原型及其模型在力学上也是相似的。要研究力学相似现象，必须从这类现象所共同遵守的规律出发。某一具体现象遵循某些具体的规律，而经典的力学现象遵循的最一般的规律则是牛顿定律，月球着陆器也不例外。在牛顿力学体系中具体规定了量的关系的定律是牛顿第二定律

(2)

式中F表示力，M表示质量，s表示位移，t表示时间。

如图1所示为月球着陆器软着陆简化力学模型，Fh为垂直缓冲力(蜂窝缓冲力假设为常值)，M为弹性支撑质量。无论是月球着陆器原型还是月球着陆器缩比模型均可简化为此力学模型。

图1 月球着陆器着陆简化力学模型Fig.1 The simplified mechanical model of lunar lander

那么，对于月球着陆器原型，其简化力学模型的运动微分方程为

(3)

同理，对于月球着陆器模型亦有运动微分方程为

(4)

式中Fp和Fm分别为着陆器原型和模型的弹性支撑质量受到的外力合力。

若月球着陆器原型与模型具有动力学相似性，则必然二者的同类物理量也成比例。根据式(3)和(4)，设月球着陆器原型与缩比模型同类物理量之间的相似常数分别为

(5)

式中cF，cM，cs，ct分别为力相似常数、质量相似常数、位移相似常数和时间相似常数。

将式(5)代入式(3)化简，并与式(4)比较得月球着陆器原型与模型的相似指标为

(6)

相似指标是由牛顿第二定律得出的探测器原型与模型的相似常数之间应满足的相互关系，表明了探测器原型与模型中各相似常数间是相互关联的。

将式(5)中的相似常数代入式(6)相似指标中，则

(7)

根据图1所示，探测器弹性支撑质量所受合力为F=Fh-Mg。取重力场相似常数cg=β为探测器模型所受重力加速度与原型所受重力加速度的比率。将探测器原型中蜂窝缓冲力表示为Fh0，重力加速度表示为g0，质量表示为M0；那么根据探测器设计原则，取不同相似模型中蜂窝缓冲力为Fh=chFh0，重力加速度为g=cgg0=βg0，质量为M=cMM0。β即为探测器原型与模型间各自所处重力加速度场的相似常数，这也是采用探测器模型模拟某目标天体表面相关重力场的关键参数。

Fp=Fh0-M0g0

(8)

月球着陆器模型中弹性支撑质量所受合力为

Fm=Fh-Mg=λ2Fh0-cMM0βg0

(9)

力相似常数可表示为

常数

(10)

因此，有

λ2=cMβ

(11)

由于λ为已知的，因此有

(12)

将式(12)代入式(11)求得

cF=λ2

(13)

由几何相似性得

cx=λ

(14)

将cF，cM和cx代入式(6)中，得

(15)

因此，月球着陆器弹性支撑质量的加速度相似常数为

(16)

1.3 基于量纲分析确定探测器相似常数

对于探测器的导出量——转动惯量，其量纲可表示为[I]=[ML2]，根据以上已知的基本量的相似常数可求得转动惯量的相似常数为

cI=λ4/β

(17)

同理，对于月球着陆器的其他导出量，速度的量纲为[V]=[LT-1]，角速度的量纲为[ω]=[T-1]，角加速度的量纲为[α]=[T-2]，由量纲分析可以分别导出相应的相似常数分别为

(18)

(19)

cα=β/λ

(20)

经过以上推导，求得了与探测器动力学相关的全部重要参数的相似常数，由此即可从某一选定的探测器原型推导出另一具有相似性的探测器模型的相关参数，此两模型具有动力学相似性

1.4 月球着陆器低重力场模拟动力学相似关系

综上所述，令月球重力场下的全尺寸模型为该探测器着陆冲击试验的原型，根据以上推导的相关公式，可以依次推导出地球重力下的全尺寸模型、地球重力下的1/3尺寸模型、地球重力下的1/6尺寸模型与原型对应的动力学相似性关系，如表1所示。

表1 不同重力场和尺寸下月球探测器模型间的动力学相似关系

Tab.1 The similarity relation of different gravitational and size for lunar lander

物理量设计原型相似常数物理量相似性关系全尺寸模型某行星表面重力(λ=1，β=1)全尺寸模型地球重力(λ=1，β=6)1/3模型地球重力(λ=1/3，β=6)1/6模型地球重力(λ=1/6，β=6)长度尺寸lλλlll13l16l重力加速度场gββgg6g6g6g缓冲器应力σ1σσσσσ面积Aλ2λ2AAA19A136A缓冲力Fλ2λ2AσFF19F136F质量mλ2βλ2βmm16m16×32m16×62m时间tλβλβttt6t18t36加速度aββaa6a6a6a转动惯量Iλ4βλ4βII16I16×34I16×64I速度vβλβλvv6v2vv角速度ωβλβλωω6ω18ω6ω角加速度αβλβλαα6α18α36α

2 算例验证

针对上述低重力模拟试验方法，论文以某型号月球着陆器为例进行验证，通过建立该探测器单腿及整机模型，并应用上述模型对不同的着陆初始条件进行动力学仿真分析，以此验证上述低重力场模拟方法的有效性及可行性。

2.1 探测器全尺寸单腿落震性能相似性分析

论文采用非线性瞬态动力学方法建立了某型月球探测器全尺寸单腿落震仿真有限元模型，如图2所示。探测器的结构和着陆区月壤均假设为刚性，探测器的机体仅有x向的平动自由度，探测器的主支柱装有二级铝蜂窝缓冲器，辅助支柱则装有可进行压缩缓冲的铝蜂窝缓冲器和可进行拉伸缓冲的拉杆，足垫与月壤间以及着陆腿机构间建立接触模型。

该全尺寸单腿落震仿真有限元模型将分别进行月球重力场和地球重力场下的落震仿真分析，仿真分析的初始条件及根据动力学相似性得到的相互关系如表2所示。

图2 着陆腿着陆冲击有限元模型Fig.2 The impact finite element model of landing

以上描述模型的两个落震分析工况初始条件的主要区别体现在所受重力场、质量和初速度的不同，但此两工况各初始条件物理量均满足各物理量的相似性关系。而最终地球重力场下的落震分析结果将按照相似性关系统一换算到月球重力场下，并与月球重力场下的落震分析结果进行对比和分析，以验证论文推导得出的深空探测着陆器动力学相似性关系。经过仿真分析，分别得到了探测器机体在不同重力场下着陆的速度和加速度变化曲线如图3，4所示。

论文根据表2中所示的相似性关系，将地球重力场下的探测器机体速度和加速度仿真分析结果分别换算到月球重力场下，并与月球重力场下的仿真分析结果进行对比。上述结果表明，经转换的地球重力场下的月球探测器速度和加速度仿真结果与月球重力场下的仿真结果几乎完全吻合，采用相似关系在地球重力场下进行试验和仿真能很好地近似得出月球重力场下的月球探测器着陆冲击性能结果。由此说明，论文基于月球探测器简化力学模型推导的相似性关系，是一个较通用的相似性关系，着陆腿模型的复杂程度不影响相似性关系，该相似性关系对拥有较复杂着陆腿的月球探测器仍然适用；采用全尺寸模型，并按照相似性关系定义试验初始条件进行试验，通过换算就能够得到所需的月球重力场下的模型试验数据，且该数据的准确性较高。

表2 单腿落震仿真初始条件及相似性数据转换关系

Tab.2 The similarity transform relation of different initial condition for single leg drop simulation

物理量设计原型相似常数物理量相似性关系全尺寸单腿模型月球重力落震分析(λ=1，β=1)全尺寸单腿模型地球重力落震分析(λ=1，β=6)长度lλλlll重力加速度gββgg6g质量mλ2βλ2βmm=430kg16m=71．67kg时间tλβλβt仿真时长t=0．15s采样步长Δt=5×10-4s仿真时长t/6≈0．07s采样步长Δt=5×10-4s加速度aββaa6a转动惯量Iλ4βλ4βII16I速度vβλβλvvv=4．5m/svv=11．023m/s

图3 全尺寸单腿落震机体垂向加速度响应曲线对比Fig.3 The comparison of the vertical acceleration for full size single leg dropping

图4 月球重力场全尺寸单腿落震机体垂向加速度响应曲线对比Fig.4 The comparison of vertical acceleration for full size single leg dropping in lunar gravity

2.2 探测器全机全柔性动力学相似性分析

论文同样基于非线性瞬态动力学方法建立了月球探测器全尺寸全机着陆冲击仿真有限元模性。探测器结构和着陆区月壤均为柔性体，探测器的机体为6自由度，着陆腿及缓冲器构型与图2所示相同，足垫与月壤间以及着陆腿机构间建立接触模型，并选取机体上顶板的中心测量点1为研究对象，如图5所示。

图5 全机全柔性探测器模型测量点位置示意图Fig.5 The measuring point position of fully flexible lander

该月球探测器的全尺寸全机着陆冲击仿真有限元模型将进行月球重力场与地球重力场下的仿真分析，仿真分析的初始条件及根据动力学相似性得到的相互关系如表3所示，探测器着陆姿态为1-2-1沿下坡着陆。

以上描述模型的两个分析工况初始条件的主要区别体现在所受重力场、质量、转动惯量、初速度和采样时间步长的不同，但此两工况各初始条件物理量均满足各物理量的相似性关系。与单腿模型相同，地球重力场下的仿真分析结果将按照相似性关系统一换算到月球重力场下，并与月球重力场下的仿真分析结果进行对比和分析, 如图6～9所示。

由图6～9可以看出，由于探测器结构柔性和月壤柔性对测量点位移和速度的影响较小，经转换的地球重力场下测量点的位置、速度仿真分析结果与月球重力场下的仿真分析结果几乎完全吻合。由于地球重力场下的加速度仿真分析结果较大，且波动剧烈，为了将仿真结果相似性关系的对比表示得更清楚，图10，11直接给出了换算后的地球重力场下的加速度仿真分析结果和月球重力场下的加速度仿真分析结果，更直观地验证了月球探测器的相似性关系对于考虑柔性影响的6自由度月球探测器的位移和速度物理量仍然适用。

由此可见，针对月球着陆器6自由度全机全尺寸模型，按照相似性关系定义试验初始条件，在地球重力场下进行柔性体全机和柔性月壤下的1-2-1工况的试验和仿真分析，仍然能够通过换算得出月球重力场下相应工况的探测器着陆冲击的试验或分析结果。此外，本算例在计及结构柔性和月壤柔性情况下，仍能得到吻合较好的对比分析结果，说明结构柔性和月壤柔性都符合相似性关系，全尺寸探测器模型的相似性模型试验可较好的考虑到探测器结构柔性与月壤柔性的动力学性能及其相似性。

表3 全机仿真初始条件及相似性数据转换关系

图6 全尺寸全机模型测量点x向位移曲线对比Fig.6 The x direction displacement of the full size lander measure point

图7 全尺寸全机模型测量点y向位移曲线对比Fig.7 The y direction displacement of the full size lander measure point

图8 全尺寸全机模型测量点x向速度曲线对比Fig.8 The x direction velocity of the full size lander measure point

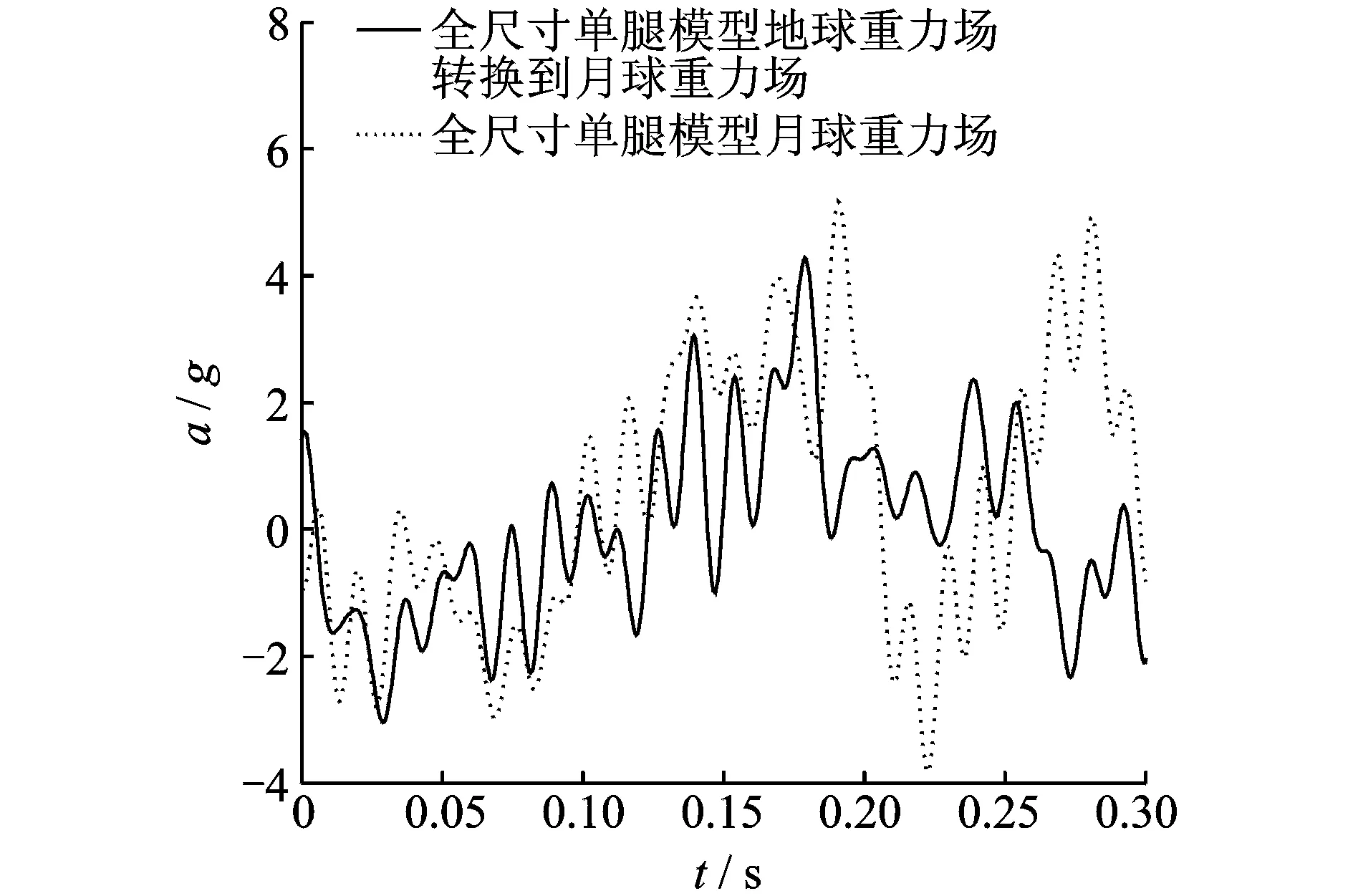
图9 全尺寸全机模型测量点y向速度曲线对比Fig.9 The y direction velocity of the full size lander measure point

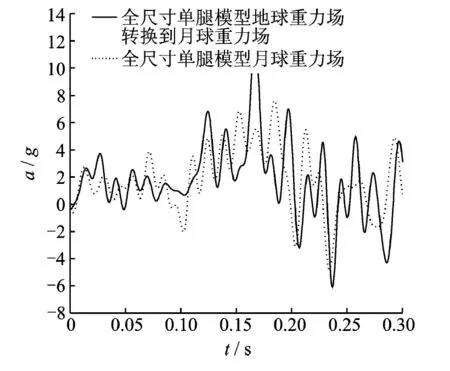
图10 月球重力场下全尺寸全机模型测量点x向加速度比较Fig.10 The x direction acceleration of the full size lander measure point

图11 月球重力场下全尺寸全机模型测量点y向加速度比较Fig.11 The y direction acceleration of the full size lander measure point

3 结 论

论文针对深空探测着陆器低重力着陆冲击试验方法开展分析和研究，通过对比分析深空探测着陆器着陆冲击试验的已有研究成果，提出了通过相似性关系模拟目标天体表面低重力的新方法，完成了以下工作：

(1) 分析了国内外深空探测着陆器着陆冲击试验现状，指出了其难点在于目标天体表面低重力场的模拟，重点介绍了常用的月球重力场模拟方法并总结了其优缺点；

(2) 结合上述优缺点，推导了深空探测着陆器动力学相似性关系和相关物理量的相似常数，提出了通过改变深空探测着陆器着陆初始条件，并对试验数据进行后续处理来模拟目标天体表面低重力场的新方法；

(3) 基于全尺寸月球探测器模型，通过对刚性单腿落震模型的计算和分析，验证了采用该方法模拟月球重力场的准确性，得出了着陆腿结构复杂程度对探测器模型相似性关系无影响的结论；

(4) 将该方法推广到了全机全柔性着陆冲击分析中，进行了相应的算例验证和分析，得出了探测器结构及月壤柔性对探测器模型相似性影响较小的结论，证明了本方法拥有较好的适应性。

由此可见，论文推导并验证的以相似性关系来模拟目标天体表面低重力场的方法具有广泛的适应性，该方法的应用为后续深空(月球、火星、小行星)着陆器的模拟低重力试验提供了简单有效的方法和可行的技术手段。

[1] 褚桂柏，张熇. 月球探测器技术[M]. 北京: 中国科学技术出版社, 2007.

Chu Guibai, Zhang He. The Technology of Lunar Probe[M]. Beijing: China Sciense and Technology Press, 2007.

[2] 陈金宝，聂宏，赵金才. 月球探测器软着陆缓冲机构关键技术研究进展[J]. 宇航学报, 2008, 29(3): 731—735.

Chen Jinbao, Nie Hong, Zhao Jincai. Review of the development of soft-landing buffer for lunar exploration [J]. Journal of Astronautics, 2008,29(3):731—735.

[3] Blanchard U J. Characteristics of a lunar landing configuration having various multiple-leg landing-gear arrangements, NASA-TN-D-2027 64N14981[R]. Langley Research Center, 1964.

[4] 王少纯，邓宗全，胡明. 一种模拟月球着陆器低重力场着陆试验方法[J]. 上海交通大学学报, 2005, 39(6): 989—992.

Wang Shaochun, Deng Zongquan, Hu Ming. An experiment method for simulating lunar lander low gravity[J]. Journal of Shanghai Jiaotong University, 2005, 39(6):989—992.

[5] Blanchard U J. Evaluation of a full-scale lunar-gravity simulator by comparison of landing-impact tests of a full-scale and a 1/6-scale model, NASA TN D-4474[R]. Langley Station, Hampton, Va.: Langley Research Center, 1968.

[6] 王希季. 航天器进入与返回技术[M]. 北京: 宇航出版社, 1991.

Wang Xiji. The Spacecraft into and Return Technology[M]. Beijing: China Astronautic Publishing Press, 1991.

[7] Parkinson R C. The use of system models in the EuroMoon spacecraft design[J]. Acta Astronautica, 1999, 44(7-12): 437—443.

[8] 齐丕骞，史惟琦. 起落架落震试验中的仿升动力模拟[J]. 机械科学与技术, 2002, 21(S2):36—37.

Qi Peijian, Shi Weiqi. Wing lift simulation in landing gear drop test.[J]. Mechanical Science and Technology, 2002,21(S2):36—37.

[9] Blancbard U J. Model investigation of technique for conducting full-scale landing-impact tests at simulated lunar gravity, NASA TN D-2586[R]. Langley Station, Hampton, Va.: Langley Research Center, 1965.

[10]Laurenson R M. Analysis of legged landers for the survivable soft landing of instrument[J]. Journal of Spacecraft and Rockets, 1973, 10(3): 208—214.

[11]Chunhui L. Microgravity science and applications[J]. Journal of Astronautics, 1996(10): 110—114.

[12]何欢, 何成, 陈国平, 等. 深空探测气囊着陆缓冲系统的原理样机动力学相似问题研究[J]. 振动工程学报, 2013, 26(4)：554—560.

He Huan, He Chen, Chen Guoping, et al. Similarity problem of the impact response of the deep space exploration airbag cushion landing system and its prototype[J]. Journal of Vibration Engineering, 2013, 26(4):554—560.

[13]姜忻良, 徐炳伟, 李竹. 土-桩-结构振动台模型试验相似理论及其实施[J]. 振动工程学报, 2010, 23(2):225—229.

Jiang Xinliang, Xu Bingwei, Li Zhu. Similitude laws and its application in shaking table test of soil-pile-structure interaction system[J]. Journal of Vibration Engineering, 2010,23(2):225—229.

Research of dynamics similarity technology in planetary landing

CHENJin-bao1，WANJun-lin2,CHENGMei3,NIEHong4

(1. College of Aeronautics Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China; 2. The Twenty-eighth Research Institute of China Electronic Technology Group Corporation, Nanjing 210018, China; 3. Shanghai Institute of Satellite Engineering, Shanghai 200011, China; 4. College of Aerospace Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China)

The difficulty of landing-impact tests of the lunar lander is the simulation of low-gravity field on the surface in lunar environment, this paper derived the law of dynamic similarity for landers, and propose a new method for simulating low-gravity field on the surface of objects outside earth, which was achieved by changing initial conditions of probe landing and by subsequent treatment of experimental data. And also the widely applicability to different lander conditions and lunar soil conditions is proved by calculation examples. Through this method to simulate the low gravity, the prototype of lander can be used with simple equipment and can be made optimization very easily. This method can be used for later lunar exploration, the Mars exploration and low-gravity simulation on other extraterrestrial objects.

lander; landing impact; low gravity simulation; similarity

2013-08-16；

2015-06-19

上海市深空探测技术重点实验室开放课题资助(13d22260100);上海航天SAST基金重点项目资助(SAST201320)

V412.4

A

1004-4523(2015)06-0871-08

10.16385/j.cnki.issn.1004-4523.2015.06.003

陈金宝(1980—)，男，博士，副教授。电话：(025)84896869；E-mail:chenjbao@nuaa.edu.cn