形貌优化在机枪枪管频率设计中的应用以及射击精度改进研究

华洪良， 廖振强， 邱 明， 李佳圣， 宋 杰

(南京理工大学机械工程学院， 江苏 南京 210094)

形貌优化在机枪枪管频率设计中的应用以及射击精度改进研究

华洪良， 廖振强， 邱 明， 李佳圣， 宋 杰

(南京理工大学机械工程学院， 江苏 南京 210094)

为了提高机枪系统射击精度，将瞬态动力学与模态分析技术相结合，为枪管结构形貌优化选择了合适的目标模态，对其进行了形貌优化。采用刚柔耦合动力学与外弹道计算对优化前后机枪系统动力学响应特性、射击精度进行了对比研究。结果表明：采用优化后的枪管结构后，枪口高低方向振动位移、速度、射角最大值分别减少了40%，52%，46%左右，效果良好。并且，机枪射击精度指标R50，R70分别由原先的7.7，11.6 cm下降为2.6，6.4 cm，射击精度指标分别提高了66%，44%左右，提升效果较为明显。此研究可为同类武器结构设计提供参考。

枪管； 形貌优化； 射击精度； 动力学； 有限元

1 概 述

随着机枪系统的轻量化设计的要求不断提高，机枪结构中总是不可避免地存在着一些刚度较差的薄弱环节，如：枪管、枪架等细长结构[1-2]。由于机枪发射为一强冲击过程，该过程中的强冲击载荷会使得刚度较差的结构发生较大的弹性变形，使机枪系统产生较为显著的结构振动[3-4]。在外弹道条件一致的情况下，机枪系统射弹散布将直接取决于弹头出枪口瞬时枪口的振动姿态上(即弹头初始扰动)，如图1所示。弹头初始扰动波动程度越大，则弹头最终散布越大，射击精度越差。为了提高机枪系统射击精度，可以对枪管固有频率进行优化设计，使其固有频率增加，则机枪在相邻两次发射期间，枪口将获得更多的振动衰减次数，弹头初始扰动波动程度也更小，从而达到提高机枪射击精度的目的。

图1 发射时枪管弯曲变形Fig.1 Bending deformation of barrel during firing

形貌优化是一种形状最佳化的方法，即在板壳结构中寻找最优加强筋分布参数来改变结构的频率与强度[5]。对结构进行形貌优化的关键是选取合适的目标模态作为目标函数。本文采用模态分析与瞬态动力学分析相结合的方法选取目标模态。

为了研究优化后的枪管结构对机枪系统射击精度的改进情况，本文根据优化得到的枪管结构建立了改进后的机枪系统刚柔耦合发射动力学模型，与原系统射击精度进行了对比研究。

2 形貌优化与动力学响应分析方法

由于枪管结构经形貌优化后不可避免地会使其质量发生变化，并使整枪动力学特性发生变化。因此，不能单独地将枪管局部固有频率作为机枪射击精度的评价指标，而是要将形貌优化、动力学计算、外弹道理论相结合，对机枪射弹散布进行定量计算，以此来作为评价机枪射击精度的依据。

分析流程如图2所示。首先，将瞬态动力学计算与模态分析方法相结合为形貌优化选择合适的枪管结构目标模态。然后，以枪管目标模态固有频率作为目标函数对枪管结构进行形貌优化。随后，根据优化得到的枪管结构建立了改进后的机枪系统刚柔耦合发射动力学模型，通过计算获得枪口动力学响应。最终，根据弹头出枪口时间，从枪口响应中提取外弹道边界条件并进行外弹道计算，获得机枪射弹散布，以此来作为机枪射击精度的依据。

图2 枪管分析流程Fig.2 Analysis process of the barrel

3 形貌优化

3.1 设计变量与约束条件

目前，结构形貌优化主要基于有限元方法进行[6-9]。将结构离散为n节点有限元模型，则形貌优化数学模型可以表述为：

(1)

s.t.gj(X)≤0 (j=1，2，…，m)，

(2)

式中X=x1,x2,…,xn为设计变量，表示节点沿结构表面法向位移量；F(x)为目标函数；gj(x)为不等式约束函数；上角标L，U分别指设计变量下限与上限。

(3)

式中VOL1为形貌优化前枪管体积；VOL2为形貌优化后枪管体积。为了使枪管满足轻量化条件，取Vf=1.2，即优化后枪管体积不能大于优化前1.2倍。

机关党员干部尤其是青年干部抽出一定时间有组织、有计划地到偏远农村去与广大农民群众“同吃、同住、同劳动”，是他们察民情、知民生、解民忧的重要途径，也是他们了解国情、走进民心、联系农民的必由之路。对于中国这样一个农业大国来说，只有进农家门，知农家情，才有助于广大机关党员干部与农民群众真正“想在一起、干在一起”，有助于机关党员干部不忘初心，牢记使命，用心走好群众路线，用情站稳人民立场，自觉永葆政治本色，忠实践行根本宗旨，始终植根于人民群众这片沃土，做称职的人民公仆，不断夯实我们党在农村执政的群众基础。

目标函数F(x)为枪管结构的某阶模态频率值，该频率值在优化过程中将被最大化，来提高枪管刚度。在此，目标函数F(x)与优化前后枪管结构体积VOL1，VOL2为有限元分析过程返回的结构响应函数。Optistruct软件允许用户自定义各种响应函数，使得该形貌优化顺利进行。

3.2 目标函数

本文对机枪系统进行了模态分析以及瞬态动力学分析，通过对比机枪发射过程中的枪管结构变形与枪管结构振型，来为形貌优化确定合适的枪管目标模态。在进行枪模态分析时，将枪管末端与节套配合处一圈节点固定约束，其前6阶模态振型如图3所示。在进行瞬态动力学分析时，机枪3个架腿采用固定约束，载荷(枪膛与导气室压力)将在本文4.1小节论述。在机枪发射过程中，结构变形如图4所示。通过对比图3与4可以发现，机枪发射过程中，枪管变形与其第2阶模态振型非常相似，该阶模态对枪口响应起到主要的贡献作用，对该阶模态振型进行修改，能够有效改进枪口响应特性，因此枪管结构第2阶模态频率为形貌优化的目标函数。

图3 枪管结构模态分析Fig.3 Modal analysis of the barrel structure

图4 机枪系统瞬态动力学计算Fig.4 Transient dynamics analysis of the machine gun system

3.3 形貌优化分析

为了节约模型计算时间，在Optistruct软件中建立有限元模型时将枪管简化为一圆形管，用壳单元模拟。形貌优化模型如图5所示，枪管与枪体配合处为非设计区域，其余部分为设计区域，二者在图5中通过不同颜色区分。非设计区域的单元通过rigid单元进行连接，用来模拟枪管与枪体的配合，该部分在计算过程中不会发生变化。而设计区域会在计算过程中发生变形，以使得枪管的一阶频率最大化，来提高枪管的刚度。为了使得优化出来的枪管易于加工，约束壳单元的变形均沿着枪管表面法线方向，且变形量小于7 mm。通过EIGRL关键字提取枪管的第1阶频率值，并将其定义为目标函数。定义优化后与优化前枪管体积比作为约束函数，约束其值小于1.2。为了使得优化得到的结构便于加工，设置linear关键字约束枪管表面变形均平行于枪管轴线方向。形貌优化模型经过7次迭代以后达到收敛，枪管结构云图如图6所示。

图5 形貌优化有限元模型Fig.5 Finite element model of topography optimization

图6 形貌优化结果Fig.6 Topography optimization result

形貌优化结果表明，在枪管整个长度方向设计加强筋结构可提高其固有频率。本文根据形貌优化得出的加强筋位置分布，在考虑枪管制造工艺性的基础上，对枪管结构进行了重新设计，如图7所示。

图7 枪管结构新设计Fig.7 New design of barrel structure

4 射击精度验证

4.1 动力学分析

机枪系统刚柔耦合发射动力学模型如图8所示，由于枪管、枪架、导气管为细长结构，刚度较差，因此在该模型中将这些结构作为弹性体考虑，其余结构为刚体。用于对比分析的两个动力学模型除了枪管结构不同，其余参数均一致，这样可以保证计算得出的结果的不同是由不同枪管结构造成，而不是其余因素导致。

图8 机枪发射动力学模型Fig.8 Firing dynamics model of machine gun

架腿与土壤的相互作用，采用通过3组弹簧与阻尼器模型实现[10]，每组弹簧阻尼器模型由3个相互正交的弹簧阻尼器构成，来模拟土壤对机枪驻锄各个方向的作用力，弹簧与阻尼器参数如表1所示。内弹道与后效期膛内压力曲线通过Matlab编程求解经典内弹道方程得到，如图9所示(P为枪膛压力，Pq为导气室压力)。在Adams中采用Spline函数进行加载，模拟机枪20连发动力学过程，获得机枪射击过程的动力学响应特性。

表1 弹簧与阻尼器力学参数

图9 枪膛压力与导气室压力Fig.9 Bore pressure and gas chamber pressure

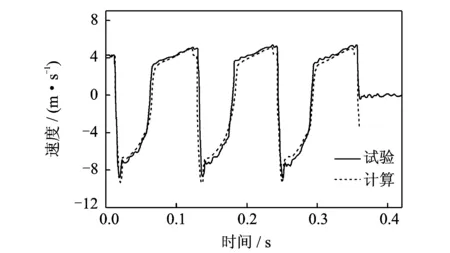
图10 机框速度Fig.10 Blot frame velocity

图11 枪口动力学响应Fig.11 Muzzle dynamic response

由于机枪发射过程中机框为主要运动部件，质量接近3 kg，其运动速度对机枪振动影响较大，通过对比机框速度便可验证模型的正确性。图10表明机框运动速度曲线计算值与试验曲线基本一致，本文建立的机枪系统动力学模型及其响应曲线可信。

枪口(图8中点C)高低方向动力学响应如图11所示，采用优化后的枪管结构后，枪口高低方向振动位移、速度、射角最大值分别由18.9 mm，5.2 m/s，1.58°下降为11.3 mm，2.5 m/s,0.86°，下降率分别为40%5，2%，46%左右，枪口振动有所减少。由于枪口方位方向振动对机枪射击精度影响较小(后续外弹道计算将说明这一点)，因此，此处只给出了枪口高低方向响应曲线。

4.2 射击精度

为了更直观地研究优化后的枪管对机枪射击精度的改进情况，本文根据弹头出枪口时间，从枪口响应曲线中提取得到了弹头出枪口瞬时初始扰动，即外弹道边界条件。弹头初始扰动如图12所示，结果表明：采用优化后的枪管结构后，弹头出枪口瞬时弹头初始扰动波动程度更小，并且波动稳定速度有所加快。

图12 初始扰动Fig.12 Initial disturbances

图13 射弹散布Fig.13 Shot dispersion

根据外弹道模型[11]，以及弹头初始扰动对机枪射弹散布进行计算，取射击距离为100 m，射弹散布结果如图13所示。其中，R50，R70含义为：包含总弹头数中50%，70%弹头的散布圆半径，图中大圆半径为R70，小圆半径为R50。外弹道计算表明，机枪射弹散布主要沿高低方向分布，这是由于枪口方位方向振动相对高低方向振动较小所致。机枪20连发R50，R70实验值分别为12.0，7.9cm，本文计算值分别为7.7，11.6cm，相对误差较小，表明外弹道计算可信的同时，动力学计算也可信，因为外弹道边界条件是从动力学响应中提取得到。

采用优化枪管结构后，R50，R70分别由原先的7.7，11.6cm下降为2.6，6.4cm，射击精度指标分别提高了66%,44%左右，提升效果较为明显。

5 结 论

(1) 本文将瞬态动力学、模态分析方法相结合，为形貌优化选择了合适的目标模态，并对枪管结构进行了形貌优化。

(2) 采用优化后的枪管结构进行20连发射击时，枪口高低方向振动位移、速度、射角最大值分别减少了40%，52%，46%左右，效果良好。

(3) 外弹道计算表明，采用优化后的枪管结构后，机枪射击精度指标R50，R70分别由原先的7.7，11.6cm下降为2.6，6.4cm，射击精度指标分别提高了66%，44%左右，提升效果较为明显。

[1] Hua H L, Liao Z Q, Song J. Vibration reduction and firing accuracy improvement by natural frequency optimization of a machine gun system[J]. Journal of Mechanical Science and Technology, 2015, 29(9):3 635—3 643.

[2] Gimm H I, Cha K U, Cho C K. Characterizations of gun barrel vibrations of during firing based on shock response analysis and short-time Fourier transform [J]. Journal of Mechanical Science and Technology, 2012, 26(5):1 463—1 470.

[3] 陈杨. 喷管气流反推减后坐武器系统关键技术研[D]. 南京：南京理工大学, 2009.

Chen Yang. Technology of reducing the recoil force by Jet gas weapon system [D]. Nanjing: Nanjing University of Science and Technolog, 2009.

[4] Hak In Gimm, Ki Up Cha, Chang Ki Cho. Characterizations of gun barrel vibrations of during firing based on shock response analysis and short-time Fourier transform[J]. Agency for Defense Development, 2012,26(5)：1 463—1 470.

[5] 于开平, 周传月, 谭惠丰. HyperMesh从入门到精通[M]. 北京:科学出版社, 2005.

[6] 王连生, 郝志勇, 景国玺,等. 基于多目标形貌优化的缸盖罩低噪声设计[J]. 西南交通大学学报, 2012, 47(6):1 064—1 068.

WANG Liansheng, HAO Zhiyong, JING Guoxi. Low noise design of cylinder head cover based on multi-objective topography optimization[J]. Journal of Southwest Jiaotong University, 2012, 47(6):1 064—1 068.

[7] 王玉兴, 郝志勇, 陈馨蕊,等. 虚拟预测-形貌优化方法在油底壳低噪声设计中的应用研究[J]. 内燃机工程, 2010, 31(3):80—84.

WANG Yuxing, HAO Zhiyong, CHEN Xinrui,et al. Application of virtual prediction-topography optimization method to low noise oil-pan design[J]. Chinese Internal Combustion Engine Engineering, 2010, 31(3):80—84.

[8] 贾维新, 郝志勇, 杨金才，等. 基于形貌优化的低噪声油底壳设计研究[J]. 浙江大学学报(工学版), 2007, 41(5):770—773.

JIA Weixin, HAO Zhiyong, YANG Jincai, et al. Low noise design of oil pan based on topography optimization[J]. Journal of Zhejiang University(Engineering Science), 2007, 41(5):770—773.

[9] 叶盛,辛勇,李长银，等. 基于正交试验-形貌优化法的钢铝复合车架设计[J]. 机械科学与技术, 2014, 33(10):1 555—1 561.

Ye Sheng, Xin Yong, Li Changyin, et al. The Design of steel-aluminum composite frame using the orthogonal test and morphology optimization[J]. Mechanical Science and Technology for Aerospace Engineering, 2014, 33(10):1 555—1 561.

[10]陈明,马吉胜,贾长治，等. 基于虚拟样机的某型机枪射击动态性能研究[J]. 计算机仿真, 2006, 23(8):192—195.

CHEN Ming, MA Jisheng, JIA Changzhi, et al. Firing dynamic characteristics of a dual-purpose machine gun based on virtual prototype[J]. Computer Simulation, 2006, 23(8):192—195.

[11]王中原, 周卫平. 外弹道设计理论与方法[M]. 北京:科学出版社, 2004．

[12]王瑞林. 大口径机枪动力学特性与射击精度研究[D]. 南京：南京理工大学, 2003.

WANG Ruilin. The researches on dynamic characteristics and firing accuracy of large caliber machine gun[D]. Nanjing: Nanjing University of Science and Technology, 2003.

Application of topography optimization in frequency design of machine gun barrel and its efficiency on firing accuracy improvement

HUAHong-liang,LIAOZhen-qiang,QIUMing,LIJia-sheng,SONGJie

(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094 ,China)

To improve the firing accuracy of a machine gun system, we optimized the barrel structure by using topography optimization, and the suitable target mode was confirmed with aids of transient dynamics analysis and modal analysis. Rigid-flexible coupled dynamic analysis and exterior ballistics calculations are carried to investigate the topography optimization efficiency on vibration reduction and finally the firing accuracy. The results show that the use of the new designed barrel structure results in a significant vibration reduction of muzzle, and the vibration in the y-direction that is displacement, velocity, firing angle are reduced by almost 54%, 41%, 38% respectively. In addition to this, the R50 and R70 is greatly reduced from 7.7 cm and 11.6 cm in the initial design to 2.6cm and 6.4cm in the optimal design, with an improvement ratio of about 66% and 44%, respectively. This paper can provide guide for similar weapon structure design.

barrel; topography optimization; firing accuracy; dynamics; finite element method

2014-04-18；

2015-03-02

国家自然科学基金资助项目(51375241，51376090)

TJ203

A

1004-4523(2015)06-0946-06

10.16385/j.cnki.issn.1004-4523.2015.06.012

华洪良(1990—),男,博士研究生。电话:15705186319;E-mail:huahl123@126.com