耦合波型的相似性对地下管道地震响应行为的影响研究

吴祚菊, 张建经, 王志佳, 吴兴序

(1.四川省建筑科学研究院， 四川 成都 610081; 2.西南交通大学土木工程学院， 四川 成都 610031)

耦合波型的相似性对地下管道地震响应行为的影响研究

吴祚菊1, 张建经2, 王志佳2, 吴兴序2

(1.四川省建筑科学研究院， 四川 成都 610081; 2.西南交通大学土木工程学院， 四川 成都 610031)

克服了传统非一致性激励输入中仅能考虑时间差动的缺点，采用小波分解与重构手段来构建一系列空间相似性耦合波型，该方法具有频率成份的含量及其出现的先后顺序可以调整的特点，因此可以模拟天然地震动中的局部场地条件突变，使一种能够满足多方面条件的非一致性输入成为可能。另外，将耦合波型的相似性与地下管道结构的动力响应相结合，通过大型振动台实验，研究了地震作用下管道结构内力随耦合波型相似性变化而变化的规律。结果表明管道结构两相邻质点间耦合波型的相似性对管道内力响应值存在着显著影响，并得到了一系列非一致性激励试验中较为重要的规律。

地震动生成； 地下管道； 耦合波型相似性； 小波分解与重构； 振动台实验

引 言

地震动输入是大型结构抗震分析中最基础，也是最关键的问题，尤其对延长型的管道结构而言，当采用传统的一致性输入时[1-2]，由于其不能考虑真实地震动中存在的空间变化，因此难以逼近延长型结构在天然地震动中真实的受力状态。所以，如何为地下管道等延长型结构提供一种合理的多点非一致性输入模式，成了该类型结构物抗震性能研究的重点和热点。

多点非一致性输入，也称为多点非一致激励，是指由于震源机制、地震波的传播特征、地形地质构造不同，使到达结构物各点的地震波在性质和时间上存在差异的现象。地震发生时，从震源释放出来的能量以波的形式传播至地面，地面上不同点处接收到的地震波由于经过不同的路径，所以其振动形式就不会完全相同。这种差异主要表现在地震波的入射方向、幅值、相位以及频谱特征等多个方面。

近年来，国内外学者对多点非一致激励开展了一系列的理论研究[3-5]，也形成了多种空间多点非一致性输入方法。但是，在传统的管道结构的非一致性激励中[6-8]，无论是单纯地将时间差动(行波效应)作为非一致性激励的全部内容，还是把完全毫无关系的两个地震记录直接作为非一致性激励输入，都是不够全面的。在文献[6]中，用控制不同点处的爆破加载时间差来模拟非一致激励，实际上仅考虑了时间差动因素的影响；在文献[7]中，用传统的时域合成法生成一系列地震动波型，以作为非一致性输入，该方法是到目前为止，结构非一致性激励研究使用最多的一种输入方法。该地震动合成模型中，包含一个地震动相干函数模型，其由相干函数模型来实现各研究质点间的空间相关性。常用的典型相干模型有Harichandran-Vanmarke模型[8]、Abrahamson模型[9]、Loh模型[10]等。

后来的研究[11]发现，由以上相干函数模型来模拟空间各质点运动的非一致性会使得各研究质点的空间相关性过高，不符合天然地震动中的真实情况。因此，文献[11]提出了在考虑时间差动的同时，还考虑了质点所在处局部场地的平均波速，这虽然在传统的分析思维上有了一定的进步，但还是没有能够考虑到频谱特性差异这一关键因素的差异。

在真实的地震动中(比如台湾SMART-1台站记录)，两相邻质点间的运动形式不只存在的时间差动(也即时间迟滞)，其在频谱特性、振动幅值、持时，PGA值等多方面都存在一定差异。

因此，本文选择了一个综合指标——耦合波型相似性，来研究其对延长型结构响应的影响规律。耦合波型的相似性是一个综合指标，它包括两列地震波在频谱特性(即各频率成分的含量以及各成分出现的时间情况)、幅值、时间差动等多个方面。从综合相似性入手，来研究其对管道结构响应的影响，为延长型结构的非一致性激励研究打开了一个全新的研究方向。但如何自由地调整两列地震波中的频率成分含量，使两列相邻地震动时程能够满足不同的内在相似性，进而生成一系列满足要求的相似性波型，以作为结构的非一致性输入，是本文所要解决的关键问题。

1 天然地震动波型的相似性分析

本文以台湾SMART-1为例，分析在天然地震动中，两相邻质点间波型的相似情况。

1.1 幅值、持时，及时间差动情况

由于以上三项指标较为直观，可由时程曲线图直观地展现出来，因此，现列举台湾SMART-1地震中I-01，M-01，O-01等3个相邻质点(3个质点的间距很小)的时程曲线如图1所示。

图1 SMART-1加速度时程曲线系列Fig.1 The acceleration time history series of SMART-1

1.2 时频特性分析

为了克服传统的频谱图仅能反应频域内的信息，完全失去了时域的特性，因此，本文采用时频分析法[12-13]，作三维频谱图，因为三维频谱图能够同步反映时域、频域内的信息，反映各种频率成分在时间轴上的分布。以上三列时程曲线的三维频谱图如图2所示。

图2 从I-01到O-01的质点频谱图Fig.2 The spectrums from point I-01 to point O-01

由图2(a)～(c)可见，尽管3个质点相距很近，但其频率成份的含量和分布还是有明显差异的。因此，作非一致性激励研究时，仅考虑时间差动、幅值调整等直观因素是不够的。

2 人工地震动中相似性波型的生成

2.1 时间差动的模拟

本文采用含行波效应因子的频域合成法公式[14]生成一系列人工地震动时程，具体如下

(1)

以上地震动模型可以求得任意质点m的傅立叶谱，通过傅立叶逆变换后，便可得到m点的空间相关性地震动的时程曲线。其中，Fm(ωj)为第m个质点的傅立叶谱，其随频率ωj的变化而变化；Δω表示频率的步长；Lmr(ωj)为功率谱矩阵开方分解后所得到的n×n式矩阵中第m行、第r列所对应的元素；φ(ωj)为空间相关性地震动相位角，本文采用有条件模拟，即从天然地震动中提取相应的相位信息来给相位角赋值。(dr-dm)ωj/va(ωj)为行波效应体现因子，其中，dr，dm分别为r点及m点的坐标，va(ωj)为视波速。

其中，用到具体参数的取值如下：

傅立叶变换阶数N=4 096；时间步长Δt=0.03 s；频率分辨率Δω=2π/(NΔt)=1.5×10-3rad/s；

场地基频ωg=10 rad/s，低频截止频率ωc=1.8 rad/s，场地阻尼比ξg=0.5，PGA=0.5g。

在式(1)中，由于行波效应因子的存在，故其生成的地震动时程系列均能体现时间差动效应。用以上合成方法，生成任意一系列间距分别为400，600 m的时程曲线如图3所示。

图3 人工地震动时程系列Fig.3 Artificially vibration time history series

在图3(a)～(c)的3条时程曲线中，红色的点状线表示该处质点振动第1 200次时发生的时刻，该点状线不断向右移动，表明地震波在不断向右传播，该现象即为行波效应(时间差动)。

2.2 时频特性的调整

由1.1节可以看出，在天然地震动中，两相邻质点间波型的差异不只是表现在时间差动上，其频率成份含量及各含量的分布也存在着或多或少的差异(如图2(a)～2(c)所示)，而这种差异的大小和形式往往是很难确定的。根据已有的地震记录显示，同样间距的两个质点，在两次不同的地震动中，其差异的表现形式就可能完全不同。尽管造成这些差异的原因是复杂的，这些差异的变化规律也是难已确定的，但在出现了这差异以后，延长型结构的响应随这些差异形式的变化而变化的规律是可以研究的，因此，该问题即为本论文的研究目标。

2.2.1 信号分量的分解

将频域合成法生成的原始信号作n阶小波分解[15-16]，即将一个原始信号分解为n个窄带信号分量的小波系数。其中，n的取值取决于信号分解的具体要求和具体土层情况。以n=3为例，形成一系列小波系数如图4所示。

图4 各信号分量的小波系数Fig.4 The wavelet coefficient of each signal component

在图4中，cd1表示第一阶高频系数，依次类推；cd3则表示第三阶高频系数，从cd1到cd3逐层分解时，各高频系数所对应的信号分量的频率逐渐降低；ca1表示第一阶低频系数，依次类推；ca3则表示第三阶高频系数，当低频系数从ca1变化到ca3，信号所包含的高频成份越来越少，高频成分逐渐被高频系数分离出去。

2.2.2 单信号分量的重构

将以上各小波系数重构，便可得到各个单信号分量，每个分量的频带范围计算式为：

(2)

an=S0-d1-d2-…-dn

(3)

以上dn表示由小波系数cdn重构出来的第n阶高频信号分量，其所包含的频段范围如式(2)所示；an表示由小波系数can重构出来的第n阶低频信号分量，其包含的频段范围为原始信号S0减去所有分解出来的高频信号分量，具体表达式如式(3)所示。图4中的各小波系数的单分量重构后，形成各信号分量如图5所示。

图5 分解出的各信号分量Fig.5 The decomposed signal component

2.2.3 信号的重构及相似性波型的生成

根据复杂场地中各土层对各频段频率的反射及吸收情况，为以上各信号分量加上不同的权值，当土层情况尚不确定，仅需要随机生成的一系列相似波型时，可随机对各分量加权后重组，便可生成一系列相似波型。由于本文的研究目标为相似性波型的相似程度对结构响应的影响，故没有结合具体某一特定场地情况，仅采用的随机加权值将各信号分量相加后，便得到了一系列相似波型，现列出其前7阶如图6所示。

图6 前7个相似性波型Fig.6 The seven similarity wave

2.2.4 相似性系数的计算

用于波型相似度计算的方法很多，主要有区域相关法[18]、动态时间归正法[19]、骨架树匹配法等[20]，本文采用的是加权平均算法[21]，其计算公式如下

S=αSAM-βSa+γPmin

(4)

式中S为相似度；α、β、γ为加权系数，可根据实际情况调整。SAM是将被测波与初始波作M次滑移比较后，得到M个相似性基数中的最大值；Sa为幅值相似度，Pmin为单周期的最小相似度。

在式(4)中，Pmin的计算较为简单，选取几个单周期计算后选取最小值即可；SAM及Sa的计算过程如下：

(5)

(6)

表1 各点波型的相似度计算

当相似度值计算出来之后，就可以根据需要选取不同相似度的波型，作为实验的输入，以便通过实验方式，研究耦合波型相似性大小对延长型管道结构响应的影响。

3 大型振动台实验

3.1 实验目的

延长型管道结构非一致性激励的实验已较多，但基本都是研究时间差动对管道结构响应的影响。而在真实的地震动中，相邻质点之间耦合地震波的差异不仅只有时间上的迟滞，在幅值及频谱特性方面也存在很大差异。因此，本文首次从相邻波型的耦合相似度这一综合指标来研究其对延长型管道结构的影响，并将此作为本次大型振动台试验的目的。

3.2 实验布置

本实验含有2个可以独立振动的差动式台面，模型剪切箱及具体的管道布置如图7所示。

图7 实验布置图Fig.7 The experiment plan

实验中，管道各截面的传感器布置如图8所示。

图8 总体截面布置图Fig.8 The cross-section arrangement plan

其中，截面1，10为位移监测截面；截面2，4，5，A，6，7，9为应变监测截面；截面3，8，B，C加速度监测截面。图8的13个监测截面中，除截面1，截面10及截面A等3个截面只布置一个位移监测点外，其余每个截面上均布置有4个加速度或应变监测点，具体情况如图9所示。

图9 传感元件布置图Fig.9 The layout of sensors

3.3 模型相似性设计

模型相似设计是确保振动台试验能够尽可能真实地反映原型动力性状的关键之一，基于目前广泛应用的 Bockingham π定理，本文采用量纲分析方法，并结合考虑模型与原型之间的材料变形应力-应变本构关系来设计本实验的相似性比例。具体数值如表2所示。

3.4 模型尺寸及实验参数

模型尺寸及实验参数如表3，4所示。

表2 模型相似比

表3 实验模型尺寸设计

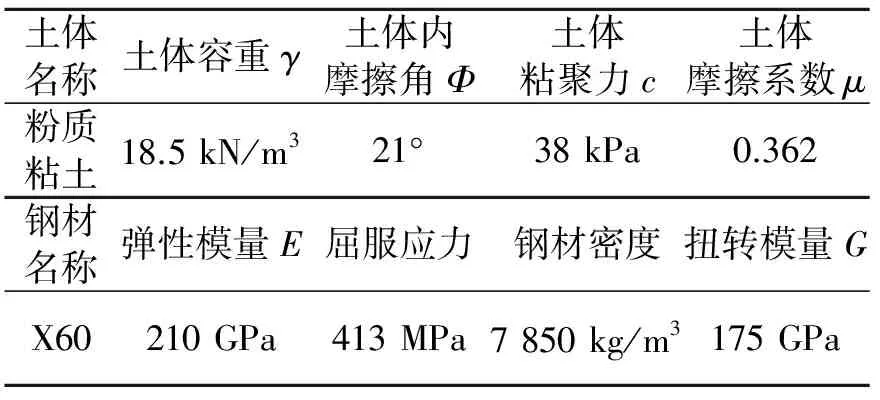
表4 土体实验参数

3.5 实验输入

本次实验中，地震动输入共分为12种工况，具体各工况如表5所示。

表5 实验工况列表

在表5中，ρ值表示左右台面输入波型的相似度计算值。

在本次实验中，地震动的入射方向为与三维坐标轴成空间45°夹角方向入射。

4 实验结果及其分析

4.1 实验过程

该实验总共分4级加载，按PGA的大小可分为0.2g，0.4g，0.6g和0.8g四种大的工况。在每一种大工况下，又分为4种小工况，即左右台面的波型相似度分别为1.0，0.6，以及0.2的工况，所以本次振动台试验共有12种工况，具体如表5中所示。在每一种工况下，都需要同时测试管道结构的加速度、位移以及轴向及直角应变化中的应变，以便研究管道结构的动力响应随耦合波型相似性变化而变化的情况。其中，直角应变花式的测量是为了测试管道结构的环向切应力。

4.2 实验现象(结果)

在该实验过程中，发现耦合波型相似性对管道结构的地震响应行为确实存在着显著影响，尤其是对管道的扭转效应而言，其影响最为显著。这种影响的显著性不仅表现在切向应力值的大小方面，其对扭转环向切应力的波形影响也十分明显。

当管道结构仅受一致性激励时(即相似度系数ρ=1.0)，环向切应力无明显的应力(或应变)峰值段出现，整个应变时程曲线呈无明显峰值波动，从始至终应变幅值均比较均匀。任取E点(位于图8截面7上)的实验结果如图10(a)所示。

由此说明，一致性激励时，环向扭转切应力对管道输入波型中的地震动峰值具有不敏感性。

当管道结构的地震动输入由一致性激励变为非一致性激励，且耦合波型的相似性逐渐降低时，扭转切应力(应变)开始逐渐增大，并在地震动输入的峰值时段内出现明显的波峰段。仍然列举质点E的具体实验结果如图10(b)所示，其具体工况见图10中标题的括号内所示。

图10 不同相似度下的扭转切应变图Fig.10 The reverse shear strain under different similarity

但是，对于管道的轴向应变而言，情况则有所不同，无论是一致性激励还是非一致性激励，其对地震动输入的峰值段均比较敏感，即在输入的峰值段时间内出现相应的应变峰值。另外，在各种工况下，轴向应变的应变值均大于环向切应变的应变值。任选取质点D(位于图8截面4上)的两个实验结果输入如图11所示，具体工况见各图中标题的括号内所示，其中，α即为PGA的取值，ρ为相似度的取值。

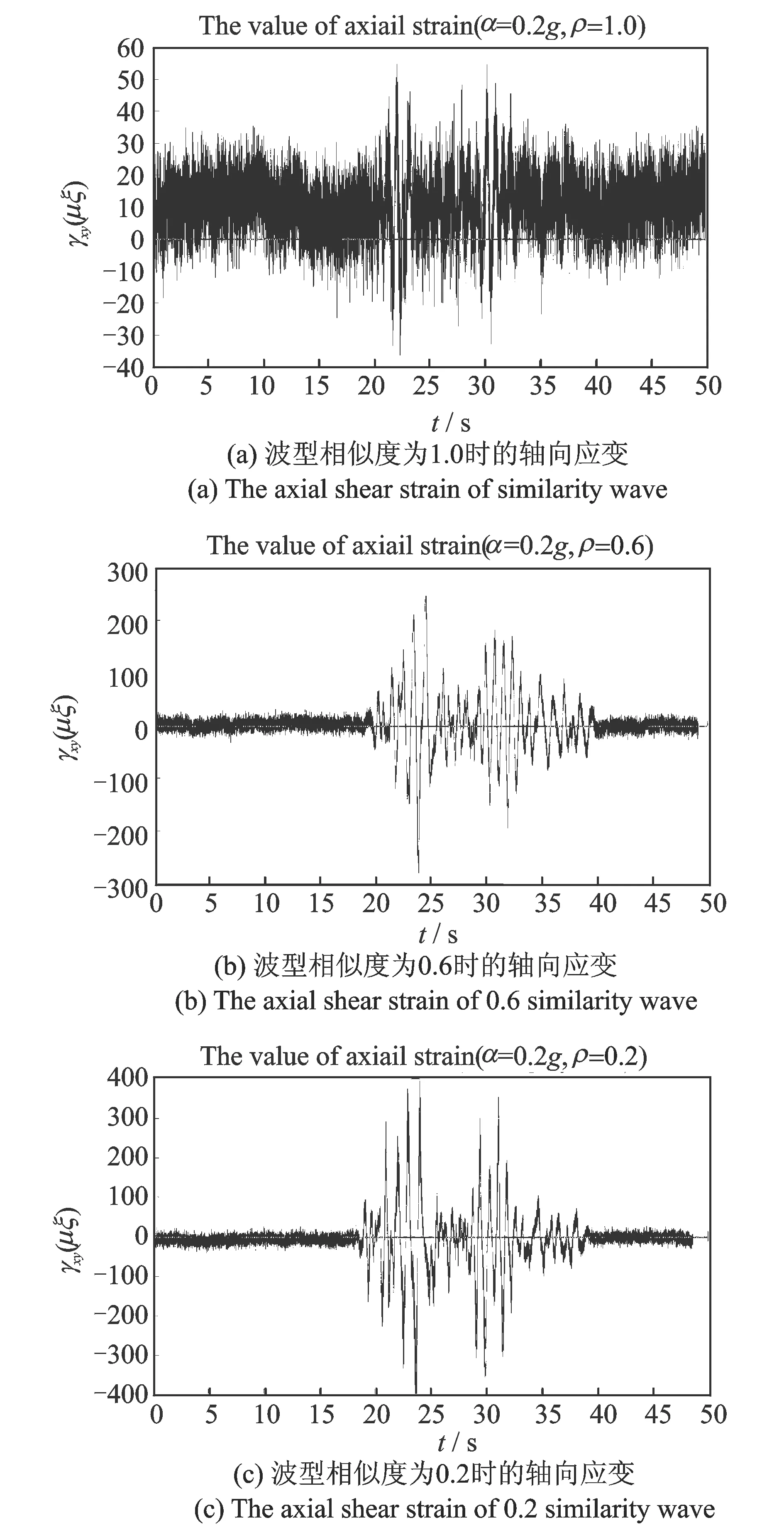
图11 不同相似度下的轴向应变图Fig.11 The axial strain under different similarity

就实验总体而言，耦合波型相似性的变化对管道结构的轴向应力和环向切应力的影响较大，但其对管道结构的加速度及位移响应的影响却很小。由于本实验设计为非破坏性实验，所以当实验结束时未能达到管道破坏，但是，可见管道的中部出现较为明显的扭转。

为了更清楚地说明各项实验结果，现将各项具体实验结果列图表分析。

4.3 实验结果分析

4.3.1 耦合波型相似性对轴向应变峰值的影响分析

选取图8中截面4上的D点为研究对象，分别在0.2g，0.4g，0.6g及0.8g四种工况下，研究该点的轴向应变随耦合波型相似性变化而变化的情况，并列出变化如图12所示。

图12 相似度对轴向应变影响分析Fig.12 Analysis of similarity influence on axial strain

从图12可以看出，当相似度ρ=1时，也即当地震动输入为严格的一致性输入时，地面峰值加速度PGA的增大并不会对管道的轴向应变产生明显影响。在本实验中，由于该轴向应变值均在弹性范围内，应变与应力对应成线性关系，因此，也可以认为当地震动输入为一致性输入时，地面峰值加速度PGA的增大不会引起管道各轴向应力值的明显增大。

但随着耦合波形相似度的降低，即随着地震动输入非一致性的逐渐增强，管道轴向应力的增大趋势非常明显。因此，从这一点来说，延长型管道结构在天然地震动中存在的多点非一致性激励现象对管道结构的抗震性能是很不利的。

4.3.2 耦合波型相似性对环向切应变峰值的影响分析

选取图8截面7上的E点为研究对象，分别在0.2g，0.4g，0.6g及0.8g四种工况下，研究该点的环向切应变随耦合波型相似性变化而变化的情况，并列出变化如图13如示。

图13 相似性对切应变影响分析Fig.13 Analysis of similarity influence on shear strain

从图13中可以看出，在PGA=0.2g，0.4g，0.6g以及0.8g的任何一种工况下，管道环向切应变峰值随耦合波型相似性降低而增大的趋势非常明显，因此，可以认为，相似度ρ的变化对环向切应变γxy的影响是显著的。

当将相似度ρ选定在某一个固定值时，环向切应变γxy会随着PGA的增大而增大，但当到达某一极限值时(本实验中为0.6g)，随着PGA的增大，γxy反而减小。同样地，在图12中轴向应变随PGA的变化趋势中也存在这一现象。为了探明这一变化趋势的原因，本文先进行了一次0.6g工况的补充实验，在实验结束之后，再将管道上方的覆盖土体逐层取出，然后仔细观察管周土体。观察时发现管周土体出现了松动，经过测试，发现刚度系数Kv有所降低(从60 MPa/m降为48 MPa/m)，因而可以推断，管周回填土体刚度系数Kv的降低可使地震作用时管道内部的轴向及环向应力减小，这一推断与参考文献[23]的结论也是一致的。

4.3.3 管道应力响应沿轴向的分布规律

1)选取PGA=0.6g时管道结构的3个耦合工况，研究其轴向应力峰值沿长度方向的分布规律，如图14所示。

图14 轴向应力沿轴向分布图Fig.14 The axial stress distribution along the pipe axial

从图14可以看出，当PGA=0.6g，地震动输入为一致性输入(ρ=1.0)时，管道的轴向应力沿整个长度方向均较小，最大值仅为18.3 MPa，位于管道沿长度方向的中间位置。当两耦合波型的相似度ρ分别为0.6和0.2时，管道轴向应力沿长度方向呈马鞍形分布，在距离管道中部约2 m的左右两侧各出现一个峰值；当ρ=0.6g时，σmax=100 MPa, 当ρ=0.2时，σmax=150 MPa。

2)任意选取PGA=0.6时的3个耦合工况，环向切应力峰值沿管道轴向分布如图15所示。

图15 环向切应力沿轴向分布图Fig.15 The shear stress distribution along the pipe axial

如图15所示，管道环向切应力沿长度方向呈抛物线形分布，最大值均发生在管道沿长度方向的中部。管道中部切应力受耦合波型相似性的影响较大，当研究截面从中间往两端移动时，相似性的影响力逐渐减弱。

4.3.4 耦合波型相似性对管道位移响应的影响分析

选取截面1上的点N为研究对象，波型相似性对管道位移响应峰值的影响如图16所示。

图16 位移峰值受耦合波型相似性影响情况Fig.16 The displacement peak affected by coupling wave similarity

从图16可知，随着输入波型相似性的增加，管道结构位移响应峰值逐渐增大，但增大趋势较弱；这一变化趋势与图12，13是相反的。在图12，13中，随着输入波型相似性的增大，到最后趋于一致时，管道内的应力是逐渐减小的，而且变化趋势显著。由此可知，地震动波型耦合相似性对管道结构的位移响应与对管道内力响应的影响趋势是完全相反的。

4.3.5 耦合波型相似性对加速度响应的影响分析

选取图8中截面3上F点为研究对象，列出耦合波型相似性对加速度峰值的影响如图17所示。

图17 加速度峰值受耦合相似度影响情况Fig.17 The acceleration peak affected by coupling wave similarity

从图17可以看出，随着耦合波型相似度的降低(从1.0下降到0.6，再由0.6下降到0.2)，除了当PGA=0.2g时加速度峰值一直无变化外，其他3条曲线的加速度峰值先由小变大，然后再由大变小；但就总体而言，地下管道结构的加速度或加速度峰值受相似度ρ的影响并不明显。

4.3.6 其他影响因素分析

在考虑管道结构动力响应的其他诸多影响因素时，温克尔地基系数Kv(地基刚度指标)为一个重要影响因素，但由于本文主要研究耦合波型相似性的影响，因此对影响因素Kv仅作简要分析：当PGA=0.6g，ρ=0.6时，截面4上D点的最大主应力峰值随Kv变化的情况如表6所示。

表6 最大主应力随Kv的变化情况

由表6中的情况可知，管道在地震作用下动力响应的剧烈程度受温克尔地基系数Kv的影响很大，当设法降低Kv(比如在管道周围填塞缓冲棉)时，埋地管道结构可取得较为满意的减震、抗震效果。

另外，管道结构的埋深、管径、壁厚、管道结构表面粗糙度，以及当地下管道穿过断层时受到的断层错动等，也都是地下管道结构动力响应不可缺少的影响因素，有关这些方面研究，前人已有过较为详细的探讨[23-24]，本文不作为研究重点。

4 结 论

地震作用下，尽管耦合波型相似性对地下管道结构的位移及加速度响应值影响很小，但其对管道内部正应力与剪应力的影响却很大。当地面峰值加速度PGA一定时，随着输入波型相似性的降低，管道内部正应力和剪应力会逐渐增大,最终在一致性输入(ρ=1)响应值的3～6倍时达到稳定。

由于在本实验中基床系数最大为90 MPa/m时管道未达破坏，因此可以判断，当基床系数不是特别大时(Kv≤90 MPa/m)，单纯的耦合波型相似性过低不会导致管道结构的破坏；只有在基床系数Kv较大且耦合波型相似性较低时，才有可能导致管道结构在地震作用下发生破坏。

通过本次大型振动台实验，得出耦合波型相似性对延长型管道结构地震响应行为的具体影响规律如下：

1)耦合波型相似度对延长型管道结构环向切应力的影响较大，随着相似度的降低，管道环向切应力逐渐增大；

2)当输入波型相似度ρ最高达1.0(即一致激励)时，管道结构的环向切应力响应无峰值段出现，整个时程曲线振动幅值始终保持均匀一致；

3)管道结构轴向应力受耦合波型相似性的影响也较大，其变化趋势与环向切应力相同，即随着耦合波型相似性的降低，该轴向应力逐渐增大；

4)耦合波形相似性对管道结构的位移及加速度响应影响较小，当研究二者的地震动响应时，几乎可以忽略管道非一致激励的影响；

5)基床系数的大小对地震中管道结构的破坏作用也具有重要影响。

[1] Ding J H, Jin X L, Guo Y Z, et al. Numerical simulation for large-scale seismic response analysis of immersed tunnel [J]. Engineering Structures, 2006, 28:1 367—1 377.

[2] Anastasopoulos I, Gerolymos N, Drosos V, et al. Nonlinear response of deep immersed tunnel to strong seismic shaking [J]. Journal of Geotechnical and Geo-environmental Engineering, ASCE, 2007，133(9): 1 067—1 090.

[3] Kiureghian A D, Neuenhofer A. Response spectrum method for multi-support seismic excitations [J]. EESD, 1992, 21:713—740.

[4] Kiureghian A D, Neuenhofer A. A coherency model for spatially varying ground motions [J]. EESD,1996, 25:99—111.

[5] Bogdanoff J L, Goldber J L, Shiff J C. The effect of ground transmission time on the response of long structures [J]. Bull. Seism.Soc.Am., 1965, 55:627—640.

[6] 陈士海,张安康,燕永峰,等. 爆破震动非一致激励作用下建筑结构响应研究[J]. 振动与冲击,2010,29(9):23—27.

Chen Shihai, Zhang Ankang, Yan Yongfeng, et al. Blasting vibration responses of structures under non-uniform excitation[J]. Journal Vibration and Shock, 2010,29(9):23—27.

[7] 孟海,陈隽,李杰,等. 地下管线-土非一致激励振动台试验研究[J]. 地下空间与工程学报,2008,4(5)：852—859.

Meng Hai, Chen Juan, Li Jie, et al. Shaking table test of soil pipe dynamic interaction under nu-uniform earthquake wave excitation[J]. Chinese Journal of Underground Space and Engineering,2008,4(5):852—859.

[8] Harichandran R S, Vanmarcke E H. Stochastic variation of earthquake ground motion in space and time [J]. J. Eng. Mech., 1986, 112:154—174.

[9] Abrahamson N A, Schneider J F, Stepp J C. Empirical spatial coherency functions for application to soil-structure interaction analysis[J].Earthquake Spectra,1991,7:1—28.

[10]Loh C H, Yeh Y T. Spatial variation and stochastic modeling of seismic differential ground movement [J].EESD,1988,16:583—596.

[11]杨海洋,钟铁毅,夏禾.铁路悬索桥纵向非一致激励地震响应分析[J]. 振动与冲击,2014,33(22):157—163.

Yang Haiyang, Zhong Tieyi, Xia He. Seismic responses analysis of a railway suspension bridge under longitudinal non-uniform excitations[J].Journal Vibration and Shock, 2014,32(22):157—163.

[12]Wu Zuoju, Wang Zhijia, Bi Junwei. Advances in environmental Technologies III ：The applied research of time-frequency analysis method employed in seismic signal processing[A]. Advanced Materials Research, 2014,955-959:1 809—1 812.

[13]Wu Zuoju, Bi Junwei, Wang Zhijia. A study of threshold denoi-sing method and its application in signal processing(ISDEA2014)[A]. Conference on Intelligent Systems Design and Engineering Applications[C]. ISDEA 2014: 88—91.

[14]吴祚菊，张建经，王志佳,等. 基于行波效应的空间相关性地震动场模拟[J]. 世界地震工程，2014,12(4):204—211.

Wu Zuoju, Zhang Jianjing, Wang Zhijia, et al. The simulation of space-related ground motion based on the traveling wave effect[J]. 2014,12(4):204—211.

[15]Mallat S. A theory of multi-resolution signal decomposition: The wavelet representation [J]. IEEE Trans on Pattern anal And Machine Intel, 1989, 11(7):674—693.

[16]Daubechies I. Ten Lectures on Wavelets[M]. Philadelphital: Philadelphital City Press,1992.

[17]Chui C K, Lian J. A Study of orthonormal multi-wavelet[J]. Applied Numerical Math. ,1996, 23: 273—289.

[18]Angrisani L, DaPonte Petal. A Measurement Method based on the wavelet transform for power quality analysis[J]. IEEE Trans. on Power Delivery, 1998, 13(4): 990—998.

[19]罗一锋,蔡嵩.基于1553B总线的接口设计与实现[J].现代电子技术, 2006, (2):55—57.

Luo Yifeng, Cai Song. Design and Implementation of the Interface Software Based on the 15538 Bus[J]. Computer Engineering & Science,2006, (2)55—57.

[20]Tuzcu V, Nas S. Dynamic time warping as a novel tool in pattern recognition of ECG changes in heart rhythm disturbances[A]. IEEE International Conference on Systems， Man and Cybernetics[C]. Los Alamitos， CA, USA, 2005: 182—186.

[21] 陆玫,包闻亮,李峰.一种波形匹配新算法V-P-V算法—用于中文签名真伪识别[J].复旦大学学报(自然科学版), 1996, 35 (5): 496—502.

Lu Mei, Bao Wenliang, Li Feng. A new waveform matching algorithm: V-P-V algorithm—used for the Chinese signature verification [J]. Journal of Fudan University (Natural Science), 1996, 35 (5): 496—502.

[22]潘琢金,王 方,周振辉. 导引头电子舱自动测试系统中波形相似性度量问题的研究[J].计算机测量与控制,2010,18(6): 1 355—1 357.

Pan Zhuojin, Wang Fang, Zhou Zhenhui. A study of waveform similarity measurement in the seeker-cabin automatic test system[J]. Computer Measurement & Control, 2010, 18(6): 1 355—1 357.

[23]王琴,陈隽,李杰. 斜入射地震波作用下地下管线的地震反应分析[J]. 华中科技大学学报(城市科学版),2008, 04:283—286.

Wang Qing, Chen Jun, Li Jie. Seismic Response Analysis of Underground Pipeline Under Obliquely Incident Seismic Waves [J] J. of HUST(Urban Science Edition), 2008, 04:283—286.

[24]王滨. 断层作用下埋地钢质管道反应分析方法研究[D].大连：大连理工大学，2011.

Wang Bing. Study on Analytical Methods of Buried Steel Pipe lines under Active Faults [D]. Dalian： Dalian University of Technology, 2011.

The research of coupling wave similarity impact on the underground pipeline structure under a seismic response

WUZuo-ju1，ZHANGJian-jing2，WANGZhi-jia2，WUXing-xu2

(1.Sichuan Institute of Building Research, Chengdu 610081, China; 2.School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031，China)

The defect had been overcome in this paper that there was only the differential time can been considered in the traditional inconsistent excitation input. The wavelet decomposition and reconstruction method was used to build a series of spatial similarity coupling waves in this paper, which can simulate the mutation of local site conditions in the natural ground motion, just because of the characteristics that the harmonic content and the order can be adjusted. So it made a way to meet all kinds of various site conditions about inconsistency input. On the other hand, the wave coupling similarity was been combined with the dynamic response of the underground pipeline structure for the first time, then a series of rule been obtained when the internal force of pipeline structure changing with the similarity of coupled waves, through this large scale shaking table test. The results show that it had a significant influence on the internal force response values, the coupling wave similarity between the two adjacent particles in the pipeline structure. Finally, a series of important rule had been obtained in this inconsistency motivation test.

the ground motion generation; underground pipes; coupling wave similarity; wavelet decomposition and reconstruction; shaking table experiment

2015-01-20；

2015-09-10

国家自然科学基金重大研究计划(41030742);国防基础科研计划(B0220133003)

P315.9；TU352.11

A

1004-4523(2015)06-0918-11

10.16385/j.cnki.issn.1004-4523.2015.06.009

吴祚菊(1978—)，女，博士研究生，高级工程师。国家一级注册结构工程师，国家一级注册土木(岩土)工程师。 电话：15928467027；E-mail：wuzuoju1234@163.com