复杂隔振结构激励下弹性基础振动及声辐射分析

孙 瑶， 杨铁军， 梁伟龙， 陈 冰， 黄 迪

(哈尔滨工程大学动力与能源工程学院， 黑龙江 哈尔滨 150001)

复杂隔振结构激励下弹性基础振动及声辐射分析

孙 瑶， 杨铁军， 梁伟龙， 陈 冰， 黄 迪

(哈尔滨工程大学动力与能源工程学院， 黑龙江 哈尔滨 150001)

针对隔振结构-弹性基础耦合结构向外声辐射问题，采用刚体理论及改进的傅里叶级数方法建立以任意边界弹性板为基础的双层隔振耦合结构数学模型。采用瑞利-里兹方法得到整个耦合结构的强迫振动响应，继而通过提取表面振速分布计算基础弹性板向外的辐射声功率。根据隔振结构的布置情况，以隔振器安装点的振动作为表征，探讨了耦合结构振动模态与基础板声辐射模态之间的耦合对应关系。最后计算并分析了基础边界条件对基础板向外辐射声功率的影响。

双层隔振； 弹性基础； 耦合结构； 声辐射； 边界条件

引 言

双层隔振是目前船用动力机械常用的隔振方式之一。不同于陆地上的设备，船舶动力机械隔振系统的设计需要考虑隔振结构和弹性基础(船体结构)的耦合作用[1-3]。不仅如此，考虑到对环境的影响及船舶噪声标准的要求，通过弹性基础向外的声辐射也一直是研究人员关注的热点。盛美萍[4]采用统计能量法及辐射效率经验公式对单层隔振-弹性基础的辐射声功率进行了估算，并分析了隔振器阻尼、设备安装位置对弹性基础声辐射的影响。张志谊等[5]以双自由度隔振模型和嵌于无限大障板中的四边简支加筋板构成的耦合结构为研究对象，采用有限元及边界元法建模，讨论了主动隔振对基础弹性板声辐射的影响。以上的研究表明，虽然最终只关心弹性基础向外的声辐射，但隔振结构的存在使施加在弹性基础上的激励情况变得复杂。因此对于隔振结构与弹性基础构成的耦合结构而言，如果仅仅是对弹性基础的振动及其声辐射进行分析不能全面地体现耦合结构基础声辐射的特性。

早期对于结构振动声辐射的研究集中于对振动模态辐射效率的分析[6]，但振动模态之间对声辐射的互耦合作用使其变得复杂[7]。20世纪90年代国外一批学者通过特征值分解对结构声辐射进行分析[8-9]。这种分析角度的优势在于各阶声辐射模态对辐射声功率的贡献独立并且不随边界条件及材料属性的变化而改变。而其不足之处在于声辐射模态形状对频率的变化不敏感，对于高频段高阶振动模态主导的情况，辐射效率高的声辐射模态也可能对辐射声功率的贡献不大。基于这两类模态各自的特性及频域上变化的不匹配性，有学者对振动模态及声辐射模态之间的耦合关系进行了研究[10-11]。如李双等[10]讨论了简支平板振动模态及声辐射模态的对应关系。其中应用了简支板振动模态奇偶模态序数的概念，但这种奇偶模态的描述方法对于非简支边界条件的弹性板却并不适用。

本文采用能量法对弹性基础上的双层隔振耦合结构进行数学建模，考虑隔振结构的多自由度运动及任意边界弹性基础的弹性振动。以隔振器安装点的运动为切入点，对耦合结构振动模态与基础弹性板声辐射模态之间的耦合关系进行探讨。这种分析方法将容易测量得到的隔振器安装位置的振动情况与耦合结构的声辐射关联在一起，为弹性基础上隔振系统的声辐射分析带来便利。

1 耦合结构系统建模

图1描述了弹性基础上的双层隔振结构基础结构声辐射产生的机理。本文考虑的双层隔振-弹性基础耦合结构如图2所示。耦合结构由上层质量(模拟机械设备)、中间质量、隔振器(上下层各采用对称布置的4个隔振器)和基础弹性板构成。图2中所示板边界的剪切弹簧及扭转弹簧可用来模拟任意边界条件，上下层隔振器如图2中所示进行编号。

图1 弹性基础上双层隔振结构声辐射耦合系统示意图Fig.1 Sketch of the vibro-acoustics of a double-stage vibration isolation system mounted on a flexible structure

图2 弹性基础双层隔振结构布置图Fig.2 A double-stage vibration isolation system mounted on a rectangular plate with arbitrary boundary condition

在忽略空间声场对结构耦合作用的假设条件下，基础弹性板向外的声辐射可以通过基础板结构振动响应的速度分布得到。其求解基本思路为：首先根据各子结构的运动情况给出其含未知系数的振动位移表达式；继而对耦合结构采用能量原理进行描述；然后采用瑞利-里兹近似方法得到系统的控制方程组；最终求解特征方程并将系数向量带回结构振动表达式中得到各子结构的振动情况。

首先，将各子结构的振动情况用含有未知系数的函数表示。对于上层及中间质量采用刚体理论建模，考虑一个平动自由度及两个旋转自由度。采用质心运动描述刚体结构的振动，其具体表达式如下：

ze=Zesinωt,θe=Θesinωt,φe=Φesinωt

zi=Zisinωt,θi=Θisinωt,φi=Φisinωt

(1)

式中z，θ及φ分别代表竖直方向、绕y轴及绕x轴的位移及角位移，下标e代表上层质量(机械设备)，下标i代表中间质量，ω为角频率，t为时间变量。待求未知系数组成的幅值向量为[Ze,Θe,Φe,Zi,Θi,Φi]T。

对于作为基础的弹性板，为不失一般性,本文采用二维改进的傅里叶级数来表示其面外弯曲振动[7]，此方法可以对任意边界薄板的弯曲振动进行描述。基础弹性板的横向位移可表示为

(2)

对整个耦合结构采用能量原理进行描述，系统拉格朗日函数可以表示成如下形式

L=V总-T总-Wext

(3)

式中V总表示耦合结构中存储的总势能，T总为耦合结构的总动能，Wext表示外力对耦合结构所做的功。

对于双层隔振-弹性基础耦合结构，其振动动能由各层质量和基础弹性板的动能构成，其势能由隔振器中储存的势能及基础弹性板的弯曲及边界势能构成，即：

V总=V上层隔振器+V下层隔振器+V基础

(4)

T总=T上层质量+T中间质量+T基础

(5)

隔振器中储存的势能可表示为：

jωce(zel-zil)2]

(6)

(7)

基础弹性板的动能和势能分别为：

(8)

(9)

式中ρ，h分别代表板的密度和厚度，D，μ分别代表板的弯曲刚度及泊松比。Kx，Ky与kx，ky分别代表基础弹性板边界上的扭转及剪切弹簧刚度，通过改变刚度值可以模拟任意的边界条件。例如，当基础板的边界条件为简支时则可以将剪切弹簧刚度设为无穷大，而扭转弹簧刚度设为0。类似地,板的自由边界条件则可将剪切及扭转弹簧刚度均设为0。

采用瑞利-里兹方法，在式(2)中取有限阶函数项来描述基础弹性板的位移。将系统的拉格朗日函数对未知系数取极值，可以得到15个线性方程组，表示成矩阵形式如下

(10)

式中E为耦合结构的未知系数向量，K，C，M及F分别代表耦合结构在缩减的拉格朗日坐标系下的刚度、阻尼和质量矩阵及外激励向量。

通过求解式(10)可以得到耦合结构在外激励作用下的未知响应的系数幅值，再代回式(1)和(2)中即可得到双层隔振结构的振动响应和基础弹性板的振动位移分布。

基础弹性板向半无限空间的声辐射应用瑞利积分计算。空间任意点声压与基础弹性板表面振速之间的关系可由下式来描述

(11)

结构的辐射声功率Wrad可由结构表面声压和法向速度表示为

(12)

式中 上标H代表共扼转置，Re()表示取实部。

如将基础弹性板分割成M个振动面元(面元的分割应保证面元几何尺寸远小于声波波长)，可对式(12)进行离散。此时，辐射声功率可以表示成矩阵形式如下

Wrad=VHRV

(13)

式中V为离散的板表面振速分布向量。R为声辐射阻抗矩阵，并且其第(m′,n′)个元素可以表示为

式中rm′,n′为板上第m′个面元到第n′个面元之间的距离，Δs为每个离散振动面元的面积。根据声辐射模态理论，对声阻抗矩阵R进行特征值分解，可以得到一组特征向量φm′及其相应的特征值{λm′}。其特征向量被视为结构声辐射的模式即声辐射模态，特征值则对应于此阶声辐射模态的辐射效率[9]。辐射声的能量可视为各阶声辐射模态辐射声功率的叠加

(15)

由式(15)可以看出，辐射声功率不仅受声辐射模态的辐射效率λm′影响，还由声辐射模态形状与振速分布的耦合程度来决定。

2 耦合结构振动及声辐射模态

本文建立的双层隔振结构及基础弹性板的几何参数如表1所示。材料的特性参数为：密度为7 800 kg/m3、杨氏模量为2×1011N/m2、泊松比为0.3。上层隔振器刚度为4×105N/m，阻尼50 N·s/m；下层隔振器刚度为1×106N/m，阻尼30 N·s/m。上下层隔振器的安装位置列于表2中。基础弹性板的边界条件为四边固支。

表1 耦合结构尺寸参数

表2 隔振器安装位置

2.1 耦合结构的振动模态

若忽略阻尼及外力的做功项，式(10)成为一个标准的特征值问题，通过求解线性特征值问题可得到耦合结构的振动模态。其前10阶固有频率与有限元计算结果的比较如表3所示：

表3 耦合结构前10阶固有频率

由上表可以看出，利用本文建立的模型计算出的耦合结构固有频率与有限元计算结果吻合良好。

绘制耦合结构的前10阶模态振型如图3所示。

为了方便探讨耦合结构模态中双层隔振结构与基础弹性板之间的耦合对应关系，本文结合隔振结构与基础的连接特性，以下层隔振器在基础弹性板上4个安装点、上层隔振器在上层及中间质量上安装点的运动情况作为表征对耦合结构中各子结构的振动形态进行描述(上下层隔振器在中间质量的安装位置虽然不同，但是由于中间质量采用刚体建模，所以采用一组安装点即可反映中间质量的振动形态)。隔振器安装点的运动状态可按隔振器编号顺序依次表示为++++，++--，+-+-及+--+(+，-表示方向相反的运动形态)。根据图3所显示振型，可将耦合结构中各子结构的运动形式列于表4中。

从图3和表4可以看出，双层隔振结构与基础弹性板的振型服从特定的耦合对应关系。如隔振器上端的运动形式为++--，则其下端只能以++--或--++的形式运动；并且由于隔振结构上下层质量采用刚体理论建模，所以不会出现对角线对称模态，即耦合结构不会出现+-+-的振动形态。此外，耦合结构前6阶模态的振型以双层隔振结构的振动为主，从第7阶模态开始耦合结构的振型主要体现为基础弹性板的振动。与单纯边界支撑的弹性板不同，下层隔振器的约束使基础弹性板的振动模态形状发生了变化，即耦合结构会出现纯板低阶振动模态的重复，而且某些纯板模态不会出现。

图3 耦合结构模态振型(1～10阶)Fig.3 The first 10 modal shapes of the coupling structure

2.2 耦合结构基础弹性板声辐射模态

根据声辐射模态理论[9,13]，对辐射声阻矩阵R进行特征值分解可以得到基础弹性板的各阶声辐射模态形状及对应的辐射效率。其前6阶声辐射模态辐射效率随频率的变化如图4所示。图5为弹性板前6阶声辐射模态形状。由于声辐射模态形状对频率变化不敏感，此处以100 Hz激励时基础弹性板的声辐射模态形状代表耦合结构在考虑频段范围内的声辐射模态形状。

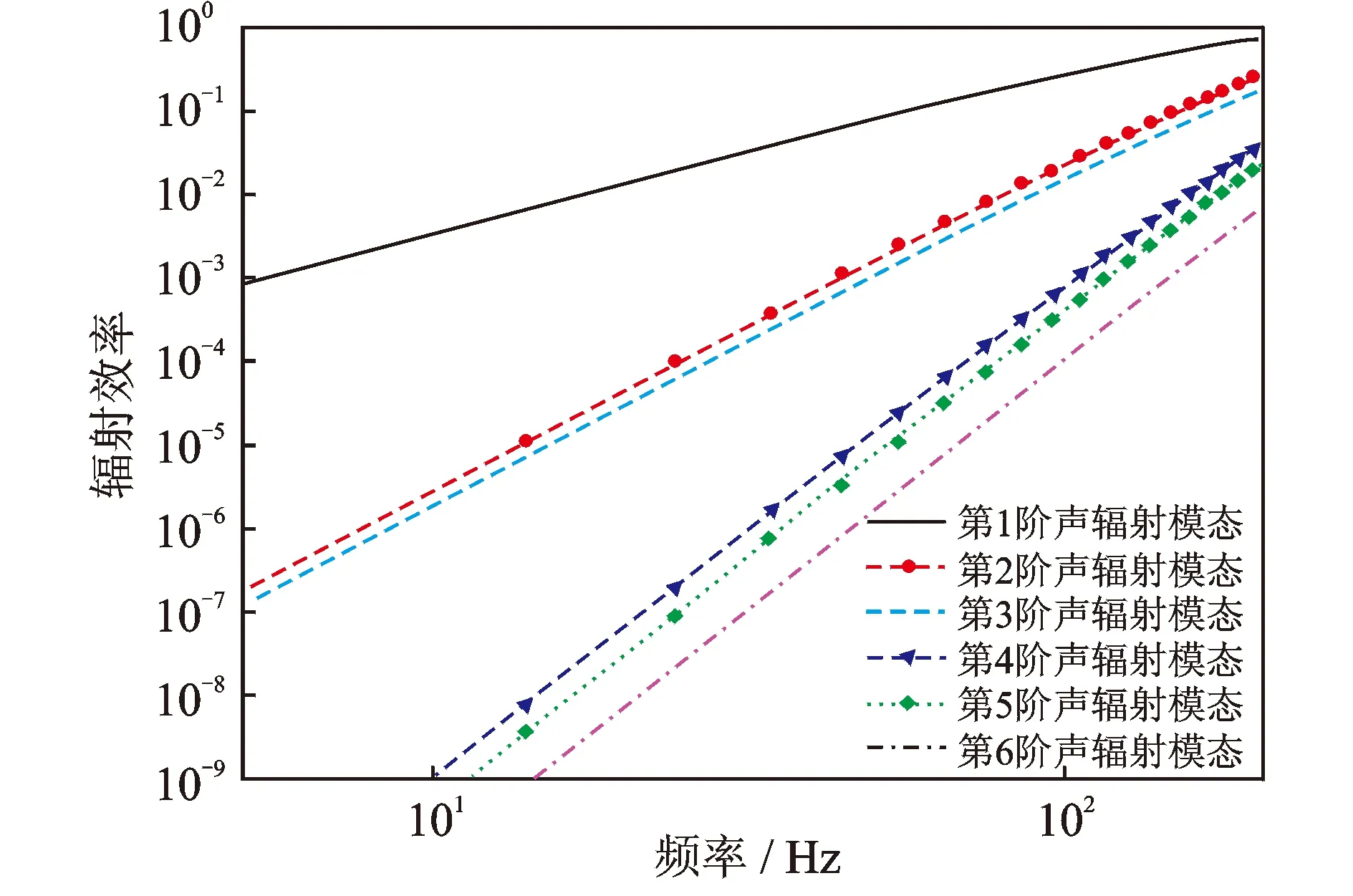
图4 基础弹性板前6阶声辐射模态的辐射效率曲线Fig.4 Radiation efficiencies of the first 6 radiation modes

图5 100 Hz激励时基础弹性板前6阶辐射声辐射模态形状Fig.5 The first 6 radiation modal shapes when exciting frequency is 100 Hz

根据对式(15)的分析可以推断，当板以特定的振动模态振动时，其与声辐射模态形状的耦合情况很大程度上影响了辐射声功率的幅值。如声辐射模态形状与振动模态形状正交则会导致辐射声功率为0。继续以下层隔振器基础安装点作为参考量，结合图3、表4及图5可以得到耦合结构的振动模态与基础弹性板的辐射声模态之间的耦合对应关系，如表5所示。

表5 下层隔振器基础安装点运动状态对应的振动与声辐射模态

Tab.5 Correspondence between vibration modes and sound radiation modes through motion styles of lower isolator locations on base plate

下层隔振器基础安装点振动形态对应耦合结构振动模态对应基础板声辐射模态++++1，4，7，101，5，6-++-2，6，82--++3，5，93+-+-无此振型4

从表5中可以看出，由于隔振器的约束，耦合结构的振动模态与基础弹性板的声辐射模态将根据下层隔振器安装位置的振动情况有选择地相互耦合，如耦合结构的1,4,7,10阶模态振动以基础弹性板的第1,5,6阶声辐射模态向外辐射噪声，而2,6,8阶振动模态则对应着第2阶声辐射模态，第3,5,9阶振动模态则对应着第3阶声辐射模态。

3 耦合结构的辐射声功率

考虑激励力作用于上层质量(0.1,0.1)处时基础弹性板各阶声辐射模态对应的辐射声功率及总的辐射声功率，计算结果曲线如图6所示。

图6 基础弹性板前6阶辐射声模态及总的辐射声功率曲线Fig.6 Sound radiation power curves of the first 6 individual radiation modes and the total sound radiation power

从图6中可以看出，在200 Hz频率范围内，基础弹性板第1，5，6阶声辐射模态辐射声功率曲线中的前3个峰值分别对应着耦合结构的第1，4和第7阶振动模态，最后一个峰值对应着耦合结构的第10阶振动模态。这和表5中显示的振动模态和声辐射模态的耦合关系一致。同样，第2，3阶声辐射模态对应的声功率曲线也呈现出与表5一致的特征。

第4阶声辐射模态的辐射声功率几乎为零，这是由于这阶声辐射模态的形状与对边相同临边相反的振动形态耦合。如表5所示，耦合结构的振型中不会产生这种对角相同临边相反的振速分布，故此阶声辐射模态对耦合结构总的辐射声功率没有贡献。

图6显示，总的辐射声功率曲线在0～100 Hz的频率范围内基本上与第1阶声辐射模态对应的辐射声功率曲线重合，然后沿第2阶声辐射模态辐射声功率曲线上行，但同时受到第3阶声辐射模态的影响，最后又回到第1阶声辐射模态辐射声功率曲线。这是因为在0～100 Hz的频率范围内耦合结构主要由前7阶振动模态主导(见表3)，不同振动模态又有选择的与1～6阶声辐射模态耦合(见表5)。由图4可知，第1阶声辐射模态的辐射效率远远大于其他各阶声辐射模态，受此影响在较低的频率范围内总的辐射声功率以第1阶声辐射模态的贡献为主。随着频率的升高，振动与声辐射模态对应的选择性逐渐显现。隔振结构第8，9阶振动模态分别只与第2，3阶声辐射模态耦合，所以总的辐射声功率曲线在结构第8阶振动模态频率附近主要以第2阶声辐射模态贡献为主，而在结构第9阶模态频率附近会受到第3阶声辐射模态的影响。但到了第10阶振动模态频率附近，第1阶声辐射模态与模态振型的高度耦合，使总的辐射声功率曲线又开始回到第1阶声辐射模态的辐射声功率曲线。

4 耦合结构的能量传递关系

本文在计算基础弹性板辐射声功率的同时还考虑了隔振系统的能量传递情况。图7为基础弹性板辐射声功率、传递至基础的功率及耦合结构总输入功率随频率的变化情况。根据耦合结构的模态振型，可以将所考虑的频率范围分为双层隔振结构振动控制区(1至6阶振动模态)和基础弹性板振动控制区(7阶振动模态之后)。

图7 耦合结构中能量传递关系及辐射声功率Fig.7 Power flow in the coupling structure and sound radiation

从图7可以看出，在双层隔振结构振动控制区范围内，传递至基础的功率流曲线与耦合结构总的输入功率流曲线在前3阶振动模态频率范围内基本一致，而在4～6阶模态频率范围内却有较大的差别。从表4中不难发现，耦合结构前3阶振动模态中双层隔振结构的两个质量与基础弹性板为同向振动，即隔振器的上下两个端面没有大的相对位移，因此隔振器的阻尼没有耗散太多的振动能量。而4～6阶振动模态中上层及中间质量反向振动，上层隔振器受到大的拉伸和压缩，隔振器阻尼吸收了一部分振动能量从而削减了传递至基础弹性板的振动功率流，同时会降低了基础板向外的辐射声功率。

对比传递功率流曲线与辐射声功率曲线，第2，3，5和第6阶振动模态虽然在传递功率流中有明显的峰值，但在辐射声功率曲线中并没有明显体现。这是因为这几阶振动模态基础弹性板的振动形式为++--和+--+，与基础弹性板的第2，3阶声辐射模态耦合(见表5)，而这两阶声辐射模态的辐射效率较低(见图4)，所以在辐射声功率曲线中没有这2阶振动模态峰值。

对于基础弹性板振动控制区，功率流传递及辐射声功率主要受基础弹性板振动的影响，而受双层隔振结构振动的影响较小，因此传递至基础的功率流曲线与基础辐射声功率曲线形状大致相同。此外，在这个区域基础弹性板的++++，++--和+--+，----(分别对应第7到第10阶耦合结构模态)振动形态在辐射声功率曲线中有明显峰值。这是因为随着频率的升高，高阶声辐射模态的辐射效率逐渐增大。由于这几阶振动模态双层隔振结构的振幅很小，而激励力作用在上层质量上，所以总的输入功率流没有明显对应的峰值。从图7中还可以看出，在基础弹性板振动控制区，双层隔振结构的下层隔振器上下两端受到压缩或拉伸，其阻尼能吸收一部分振动能量，所以传到基础的功率流较总的输入功率流有较大的衰减。

上述分析表明：相对于振动模态或者声辐射模态，隔振器的振动形态信息可以更加简便地反映弹性基础辐射声功率的情况，这对于振动主动控制传感及控制策略有一定的指导意义。

5 基础弹性板边界条件影响

由于基础弹性板结构边界上所有弹性约束的贡献被包含在基础板的势能表达式中，各种不同的边界条件可以通过设置约束的弹簧刚度系数从零到无穷大范围内的任何数值来表示，所以可以方便地考察基础弹性板的边界条件对其声辐射的影响。

参照图2将y方向扭转弹簧刚度Ky设定为0，将剪切弹簧刚度ky分别设为5×105,1×106及1×1011(与Ky值组合对应着简支边界条件)，可以得到三组不同边界条件下的基础辐射声功率、声功率与传递功率流的比值曲线如图8所示。从图中可以看出，随着剪切弹簧刚度的降低，耦合结构的固有频率降低，并且这种固有频率的偏移在基础弹性板振动控制区域更加明显。结合图8(b)可以看出随着剪切弹簧刚度的降低，辐射声功率幅值呈升高趋势，振动能量转化成声辐射能量的比例增大。

类似地将y方向剪切弹簧刚度ky值设为1×1011，将扭转弹簧刚度Ky分别设为0(与ky值组合对应着简支边界条件)、1×105及1×1011(与ky值组合对应着固支边界条件)，得到的基础板辐射声功率、声功率与传递功率流比值如图9所示。与图8相似，随着边界上扭转弹簧刚度的降低，共振峰频率变小，共振峰幅值升高。

图8 y方向剪切弹簧刚度的影响Fig.8 Effects of ky

图9 y方向扭转弹簧刚度的影响Fig.9 Effects of Ky

由式(13)可知，辐射声功率是由受边界条件影响的速度分布向量与不受边界条件影响的声辐射阻抗矩阵决定，而改变边界上的刚度在一定程度上改变了弹性基础板振动响应的速度分布。同时式(15)表明，辐射声功率的幅值与振动模态及表面振速的耦合程度有关，即声辐射模态与振动模态形状的耦合程度决定了辐射声功率的幅值。考察图5可知，声辐射模态形状与边界约束较小时的振动模态很相近，即其与边界刚度较小时振动模态的耦合度更高。所以当弱边界约束的弹性板振动时，其辐射声功率占输入功率的比值会比强边界约束时大。

6 结 论

本文对双层隔振-弹性基础的耦合结构采用能量法建模，计算了任意边界基础弹性板向半无限空间的声辐射情况。结合隔振器安装点的振动情况建立了耦合结构振动模态与基础辐射声模态之间的联系。结果表明隔振器在基础安装点的振动形态信息可以更加方便地反映辐射声功率的情况。

双层隔振结构对于基础弹性板声辐射的影响表现为：1)隔振结构的存在不仅使基础弹性板受到与隔振器相同数目的激励，同时也是对基础弹性板的约束，这使耦合结构振动模态与基础弹性板的声辐射模态有选择地耦合；2)在双层隔振结构振动控制区，传递至基础的振动能量由隔振结构的振动决定，耦合结构振动形态与声辐射模态的耦合程度关系到弹性基础的声辐射能量；3)对于基础振动控制区，声辐射能量及传递功率流均由基础板的振动响应决定。

隔振结构对基础弹性板的约束及其在低频段的主导作用，使与其耦合的基础弹性板呈现出不同于单独平板的振动形态。并且有别于单独平板振动模态从低阶向高阶的形状变化，耦合结构中的基础板振动形态会出现纯板低阶模态的几次重复。此外，某些单独平板的振动模态有可能不会在耦合结构的基础板振动中出现。

通过改变基础弹性板的边界条件，计算了基础弹性板辐射声功率、声功率与传递功率比值的变化。结果表明：边界刚度的降低使系统共振频率下降，并且这种下降趋势在基础板振动控制区表现得更加明显，而辐射声功率的幅值随着边界刚度的降低而升高。

[1] Soliman J I, Hallam M G. Vibration isolation between non-rigid machines and non-rigid foundations[J]. Journal of Sound and Vibration, 1968, 8: 329—351.

[2] Pan J, Pan J Q, Hansen C H. Total power flow from a vibrating rigid body to a thin panel through multiple elastic mounts[J]. The Journal of the Acoustical Society of America, 1992, 92: 895—907.

[3] Gardonio P, Elliott S J, Pinnington R J. Active isolation of structural vibration on a multiple-degree-of-freedom system, part I: the dynamics of the system[J]. Journal of Sound and Vibration,1997, 207: 61—93.

[4] 盛美萍，王敏庆，刑文华，等. 单层隔振系统中弹性基座的振动与声辐射特性[J]. 机械科学技术, 2000，19: 94—96.

Sheng Meiping, Wang Minqing, Xing Wenhua, et al. Vibration and structure-borne sound of supporting structures in machine vibration isolating systems[J]. Mechanical Science and Technology, 2000，19: 94—96.

[5] Zhang Z, Chen Y, Yin X, et al. Active vibration isolation and underwater sound radiation control[J]. Journal of Sound and Vibration, 2008, 318:725—736.

[6] Wallace C E, Radiation resistance of a rectangular panel[J]. The Journal of the Acoustical Society of America, 1972,51: 946—952.

[7] Li W L， Gibeling H J. Determination of the mutual radiation resistances of a rectangular plate and their impact on the radiated sound power[J]. Journal Sound and Vibration, 2000, 229:1 213—1 233.

[8] Borgiotti G V. The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurements[J]. The Journal of Acoustic Society of America, 1990,88:1 884—1 893

[9] Elliott S J， Johnson M E. Radiation modes and the active control of sound power[J]. The Journal of the Acoustical Society of America,1993, 94(4): 2 194—2 204.

[10]李双,陈克安. 结构振动模态和声辐射模态之间的对应关系及其应用[J]. 声学学报, 2007, 32(2)：171—177.

Li Shuang, Chen Kean. The relationship between acoustic radiation modes and structural modes and its applications[J].ACTA ACUSTICA, 2007, 32(2)：171—177.

[11]黎胜，赵德有. 结构声辐射的振动模态分析和声辐射模态分析研究[J]. 声学学报, 2004，29(3):200—208.

Li Sheng, Zhao Deyou. Research on modal analysis of structural acoustic radiation using structural vibration modes and acoustic radiation modes[J].ACTA ACOUSTICA,2004，29(3):200—208.

[12]Li W L, Zhang Xuefeng, Du Jingtao, et al. An exact series solution for the transverse vibration of Rectangular plates with general elastic boundary supports[J]. Journal of Sound and Vibration,2009, 321:254—269.

[13]Fahy F J, Gardonio P. Sound and Structural Vibration: Radiation, Transmission and Response[M].Academic Press, 2007:165—172.

Vibration and sound radiation from a flexible base excited by a complex vibration isolation structure

SUNYao,YANGTie-jun,LIANGWei-long,CHENBing,HUANGDi

(Power and Energy Engineering College, Harbin Engineering University, Harbin 150001, China)

The mathematical model of a double-stage vibration isolation system mounting on a flexible plate was established from the viewpoint of energy in this paper. The masses of double-stage vibration isolation system were regarded as rigid bodies whereas the flexible base plate was described using a modified Fourier series expansion which permits arbitrary boundary conditions. By using Rayleigh-Ritz method, the forced responses of the coupled structure could be obtained and the sound radiation power from the base plate could be evaluated employing Rayleigh integral. Furthermore, the coupling between vibration modes of the coupling structure and sound radiation modes of the plate was discussed. In addition, the influence of boundary conditions upon sound radiation was analyzed.

double-stage vibration isolation; flexible base; coupling structure; sound radiation; boundary condition

2014-12-08；

2015-07-28

国家自然科学基金资助项目(51375103)

O328； TK421.6

A

1004-4523(2015)06-0902-08

10.16385/j.cnki.issn.1004-4523.2015.06.007

孙瑶(1987—)，女，博士研究生。电话：(0451)82589199-306;E-mail: sunyao@hrbeu.edu.cn