基于多模式时间最短的公铁联合军事运输路径优化

吴 洋，张艳萍，李遂汝

(军事交通学院国防交通系，天津300161)

新时期，在我军质量效能型建设思想的指导下，军事运输路径研究已经受到作战部门的广泛重视，新提出的联合作战构想的关键环节就是联合投送能力。目前，对成建制部队“人装一体”联合军事运输研究较少，使得现有的军事运输路径优化模型与实际军事运输任务需求存有明显差距［1－4］，所以亟待建立贴近成建制部队“人装一体”公铁联合军事运输的路径优化模型。由于时间是部队输送的重要约束条件，而部队能否在规定的时限范围内到达指定地域又是影响作战进程并事关战争结局的重要因素。基于此，本文在已构建的多模式交通网络图基础上［5］，结合军事运输实际，建立以时间最短为目标的公铁联合军事运输路径优化模型，并采用遗传算法进行求解。

1 问题描述与条件假设

1.1 问题描述

西部某战区由于地域冲突加剧，为防止冲突升级、事态扩大、领土安全受到威胁，某部接到敌情通报和上级下达的部队输送命令，于输送时限t限时间内，从驻地O输送至目的区域D，担负自卫反击作战任务。根据当地交通布局的实际情况，只能选取铁路和公路两种运输保障方式，实施“人装一体”运输。鉴于此次部队输送任务紧急且立足于国土范围之内，故暂不考虑运输费用和运输警戒问题。

1.2 条件假设

由于实际军事运输涉及面较广、内容较多、要求较严格，为了便于探讨建模方法，故将实际情况进行一定的合理化假设，假设条件如下。

(1)设定转换次数。若首选公路运输，则公铁转换不多于两次。若首选铁路运输，则公铁转换不多于一次。

(2)抽象转换点。铁路网中车站作为转换点也代表该车站所在城市，公路网中城市作为转换点也代表城市内的铁路车站。

(3)区域化起始点。起始点根据输送要求，既可以代表城镇也表示该城镇所在区域。

(4)城市内到铁路车站的公路运输区段忽略不计。

(5)高速公路等收费站通道建筑限界满足重装备通行需求。

2 建立数学模型

2.1 多模式交通网络［5］

运用多模式网络建模和图论的相关理论与方法，建立公铁联合军事运输网络图G(V，T，E，M)，包含铁路子网图Gu(Tn，Eu，Mn)和公路子网图Gg(V，T’n，Eg，M’n)，即 G={Gu，Gg}。某战区公铁联合军事运输网络示意如图1所示。

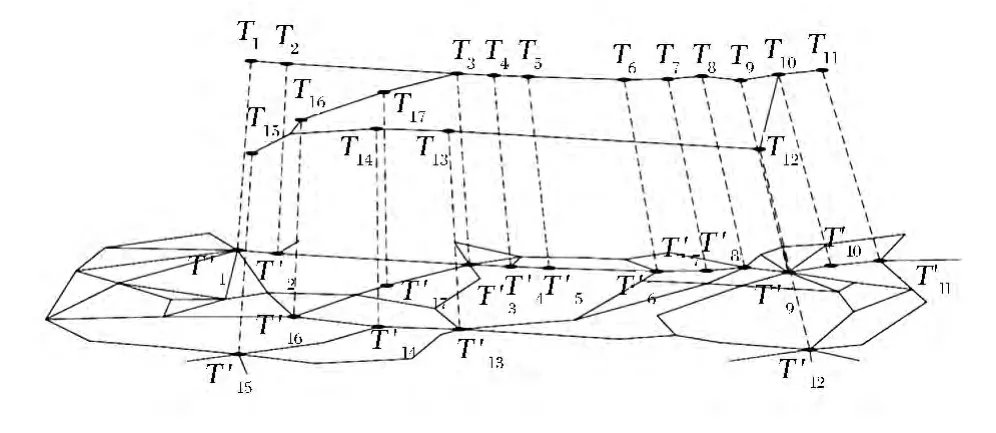
图1 某战区公铁联合军事运输网络示意

2.2 铁路目标函数

铁路军事运输时间消耗主要包括列车运行时间、中转换乘时间和等待发车时间。设列车运行时间为t运，也是部队在铁路上的机动时间;中转换乘时间为t中，仅指铁路转换到公路的装卸载时间(包括部队装备装卸载和人员乘降时间)，表示为;等待发车时间为t待，即指联合检查和人员乘载完毕后直到列车开车时止所消耗的时间(其中包括多梯队连续装载的间隔时间和梯队序列发车的等待时间)，表示为tTi。

设 t铁为铁路时间目标函数:t铁=t运+t中+t待，即

2.3 公路目标函数

公路军事运输时间消耗主要包括公路输送时间和中转换乘时间。设为部队公路机动的时间即公路运输的运行时间，由于公路网节点的特殊性，它包括锚泊点V和公路网转换点，故而产生了4种输送时间表示方式:第1种是从锚泊点Vi到锚泊点Vj的运行时间;第2种是从锚泊点Vi到转换点的运行时间第3种是从转换点到锚泊点Vi的运行时间第4种是从转换点到转换点的运行时间为公路转换到铁路装卸载所消耗的中转换乘时间

设 t公为公路时间目标函数:t公=t＇运+t＇中，即

2.4 公铁联合模型

根据路网的构成方式为分层式网络，故公铁联合模型是将铁路时间目标函数与公路时间目标函数相结合，从而构建复合网络的时间目标函数。

设t为公铁联合模型的时间目标函数:

即为

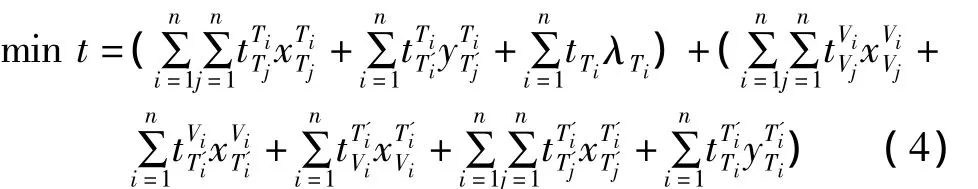
约束条件:

式中:t≤t限，为总时间约束，代表所有消耗时间不能超过输送时限。∈{0，1}，为在铁路子网内两个转换点之间的路径，当约束为0时，表示此路径不被选取，当约束为1时，为通过此路径。{0，1}，为在公路子网内两个锚泊点之间的路径，当约束为0时，表示此路径不被选取，当约束为1时，为通过此路径。∈{0，1}为在公路子网内锚泊点到转换点的路径，当约束为0时，表示此路径不被选取，当约束为1时，为通过此路径。∈{0，1}，为在公路子网内转换点到锚泊点的路径，当约束为0时，表示此路径不被选取，当约束为1时，为通过此路径。∈{0，1}为在公路子网内两个转换点之间的路径，当约束为0时，表示此路径不被选取，当约束为1时，为通过此路径。∈{0，1}和∈{0，1}，为中转换乘状态，当时表示在铁路子网内发生方式转换;当时表示在公路子网内发生方式转换;当且表示不发生方式转换。或，为保证内部运输方式一致性的判断条件，若且，则，否则，表示在转换点Tj从铁路子网转换到公路子网;同理，另一不等式表示在转换点Ti从公路子网转换到铁路子网，保证各子网内运输方式的一致性。当，表示在公铁联合军事运输网络中，只发生一次方式转换。

3 算法设计

3.1 染色体编码

本文采用符号编码方法。染色体的基因由转换点集T和锚泊点集V的混合符号组成，其排列顺序代表从出发点到目的点的路径。

设路网的转换点集合T中节点个数为n，锚泊点集合V中节点个数为m。染色体的基本位数为n+m，其基因构成为:第1位设为出发点的符号“O”;紧接着是转换点集T和锚泊点集V的混合符号节点，然后是目的点符号“D”。设染色体中从“O”到“D”的基因个数为(n+m+2)个，记为有效基因数。若除“O”和“D”两个符号外，其余符号个数不足(n+m)个，则在符号“D”后补“0”，使基因总数保持为(n+m+2)个。确定染色体中的基因第1位必是符号“O”，最末端不为“0”的基因一定是目的点符号“D”，其他基因构成只含有转换点集T和锚泊点集V的混合符号。若基因中含有“0”基因，则表示有部分转换点和锚泊点没有出现在该染色体构成的可行路径范围内。

3.2 初始群体生成

根据染色体的编码规则，已经确定每个染色体基因中一定包含出发点符号“O”和目的点符号“D”的基因，每个染色体基因总数为(n+m+2)。若随机改变染色体个体内除符号“O”和“D”外的其他有效基因序列，则将产生新的初始群体。首先通过检验初始染色体个体，若出现让染色体中两个相邻的基因生成的有效路径数不足该路径总数一半的情况，则剔除该染色体，继续寻找符合条件的染色体个体;其次是将初始生成量的规模成倍增大，挑出在路径上比较合理的个体添加到初始群体内。

3.3 适应度函数建立

适应度函数由时间目标函数的倒数构成，即

3.4 染色体选择

在此选用改进的盘赌选择法。面对新个体的选择时，首先利用多选一的原则确保选择出的下一代是在当前代中的最佳个体，然后经过盘赌方式选出其他适应度较大的个体。假设初始群体的个体数为K，各染色体的适应值为f1，f2，…，fK，则染色体所被选择的概率为

3.5 染色体交叉

交叉运算直接关系到下一代染色体的组成，对进一步优化操作具有关键性作用。由于本文路网存在两个节点集且染色体采用符号表码方式，染色体交叉可能出现新生成的染色体不在同一层路网中且互不连通。因此，为保证新染色体的良好连通性，本文采用路径交叉法，此方法是由文献［6］中提出的最佳费用的路径杂交算子基础上改进而来。该方法具体描述如下:

染色体A:{O V1T1T3T4V4V6D 0 0 0 0}可以分为运输段和转换弧

染色体B:{O V1V2T2T1T3V5V6D 0 0 0}可以分为运输段和转换弧

以选择转换弧M为原则，将染色体A和染色体B进行交叉操作。此处选择染色体A中的转换弧M4对应路径是T4－V4，染色体B中的转换弧M3对应路径是T3－V5参与交叉。如果交叉操作后，新染色体的基因节点与交叉路径节点重合，则将重复节点合并为一个节点，若基因节点数不足，则在“D”后以“0”补足;如果交叉操作后，新染色体内的基因节点与交叉路径节点之间不连通，则需插入一个使其相互连通的节点，若基因节点数大于总基因数，则删除“D”后的“0”;如果交叉操作后，新染色体内的基因节点与交叉路径节点间多出一个多余节点，即多余节点删除后不影响其左右节点的相连，则删除多余节点，并在“D”后增减“0”，以确保路径连通且存在于路网内。

3.6 染色体变异

在产生新染色体时，为了避免陷入局部寻优的不利情况，引入染色体变异机制，已便于跳出局部寻优达到全局寻优的目的。为保持良好的连通性，本文采用基本位变异的方法。在染色体符合“O”和“D”之间的有效长度中找出最后一个转换点Ti，将其变换为与Ti上一节点相连的其他节点，若变异后的染色体有效长度发生变化，则自动增减“D”后的“0”个数。

通过上述算法设计，给出运用该算法解决基于时间最短的公铁联合军事运输路径优化模型的求解流程(如图2所示)。

4 应用算例

以西部某战区某一输送梯度执行应急任务为例。该输送梯队根据上级指示安排，从驻地出发，可依靠铁路和公路两种运输方式，机动到指定目的地域，要求于24 h之内完成输送任务。该输送梯度包括若干人员和装备，其中重型装备为某式主战坦克［5］。

图2 遗传算法求解基本流程

建立该战区公铁联合军事运输网络图(如图1所示)［5］。由于军事运输与民用客货运存在较大差异，故不能按民用运输的时间来推算军事运输时间。在此假设该输送梯队通过铁路子网各运输段的时间见表1，发生中转换乘及等待时间见表2，通过公路子网各运输段的时间见表3。

表1 铁路子网各运输段通行时间

设出发地为O点，其路网内对应节点为V12;目的地为D点，其路网内对应节点为V37。根据网络节点数可知，染色体的基因总数为17+48+2=67个。设遗传算法的群体大小设定值等于400，路径交叉概率设定值等于0.85，转换点变异概率设定值等于0.05，最高叠代300次。模拟迭代次数为600次。

表2 中转换乘及等待时间

表3 公路子网各运输段通行时间

对求出的此条最优路径进行评估。按军事运输的相关规定，配有履带式重装备的成建制部队机动时首选铁路运输方式，但在某战区内未跨越战区范围，且该输送梯队规模不大，配属某式坦克数量不多，可以装载到公路大型平板拖车上运输，因此，只采取公路运输方式符合军事运输规定，所求最优路径切实可行。

5 结语

为深入贯彻落实习主席“能打仗、打胜仗”的强军目标，充分发挥各种运输方式的优势，联合军事运输将成为我军机动的重要手段。除时间外，保障能力、通过能力等因素在实际情况中也制约着军事运输组织保障工作，下一步将在时间最短的基础上研究多目标联合军事运输路径优化问题，为提升我军战略投送能力提供技术与理论支持。

［1］ 李岩，戴明强，温林.基于运输风险的战时运输网络交通流分配模型［J］.兵工自动化，2009(2):22-24.

［2］ 杨文索，姚金凯，王耀.战区内战时军事运输路径优化研究［J］.物流科技，2009(4):88-90.

［3］ 常刚，刘宝新，宋凯.应用灰色评价理论选择最优军事运输方式研究［J］.数学的实践与认识，2007(3):57-63.

［4］ 许国银，熊孝和，林涛.基于GASA算法的成品燃油战时公路配送路径优化［J］.解放军理工大学学报:自然科学版，2007(2):180-185.

［5］ 吴洋，李瑞敏，王晓安.基于多模式的公铁联合军事运输网络图模型研究［J］.公路工程，2013(6):54-59.

［6］ 刘敏.多目标遗传算法在车辆路径优化中的应用研究［D］.湘潭:湘潭大学，2006.