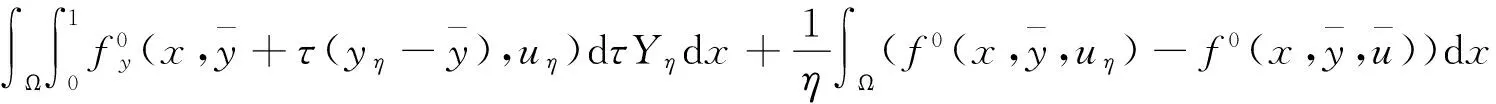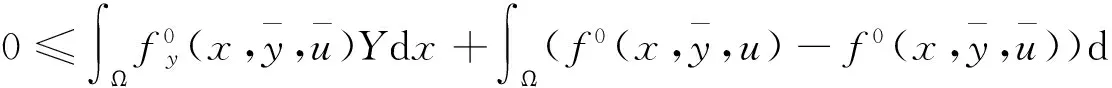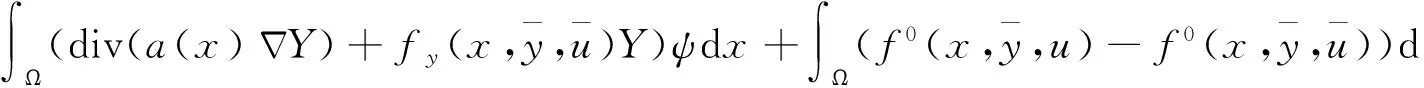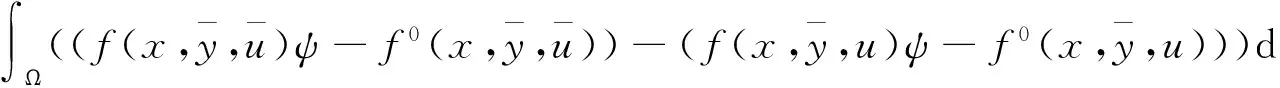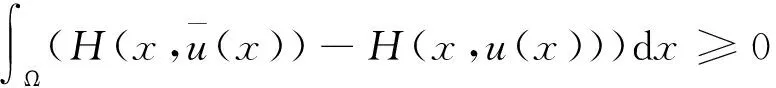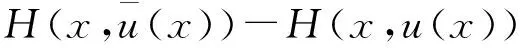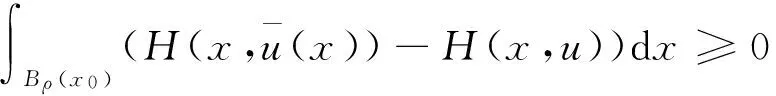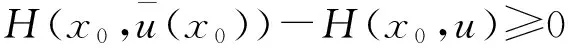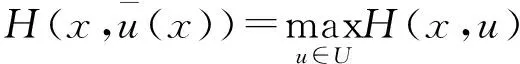一类退化半线性椭圆方程支配系统的最优控制条件
张 敬,高 夯
(1.齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161006;2.东北师范大学数学与统计学院,吉林 长春 130024)
一类退化半线性椭圆方程支配系统的最优控制条件
张 敬1,高 夯2
(1.齐齐哈尔大学理学院,黑龙江 齐齐哈尔 161006;2.东北师范大学数学与统计学院,吉林 长春 130024)
研究了一类由退化半线性椭圆方程所支配的分布参数系统的最优控制问题.当退化点集的测度为零时,利用正则化方法和变分思想,得到了该分布参数系统最优控制所满足的必要条件.
退化半线性椭圆方程;最优控制;正则化方法;变分思想;最大值原理
1 问题的提出
1986年E.Casas在文献[1]中研究了一类带有第一类边界条件的线性椭圆方程的最优控制问题,从而开始了椭圆系统的最优控制问题研究.随后J.F.Bonnans和D.Tiba等人先后在文献[2-4]中研究了半线性椭圆系统的最优控制问题.伴随着近年来对退化半线性椭圆方程研究工作的不断开展[5-8],退化半线性椭圆系统的最优控制问题逐渐成为一个新的研究课题.
本文讨论退化半线性椭圆方程支配的系统
(1)
其中Ω⊂Rn(n≥2)是具有光滑边界∂Ω的有界区域.∀x∈Ω,控制函数u(x)∈U,而U为Rm中的有界闭集.
作如下假设:
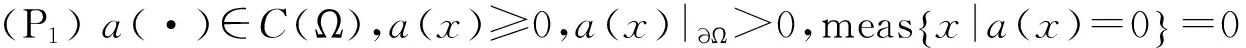
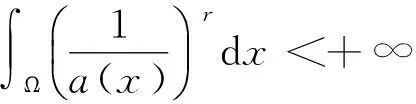
(P2)f:Ω×R×U→R满足:∀(y,u)∈R×U,f(·,y,u)是有界可测的;∀(x,u)∈Ω×U,f(x,·,u)∈C1(R);∀(x,y)∈Ω×R,f(x,y,·)∈C(U);且∀(x,y,u)∈Ω×R×U,-α≤fy(x,y,u)≤-β,α与β为正常数.
注1 若取a(x)=|x|α,αr<1,Ω=B1(O)⊂Rn,则|x|α满足(P1)所有假设条件.
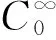
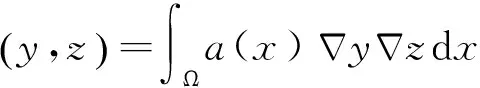
定义范数
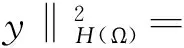
定义1 称y(·)∈H(Ω)是方程(1)的一个广义解,当且仅当对任意的φ∈H(Ω),
(y,φ)=∫Ωf(x,y,u)φdx.
引理1[5]假设(P1)—(P2)成立,对任意的u(·)∈Uad,方程(1)存在唯一的广义解y(·)∈H(Ω).
在Uad上定义指标泛函
J(u(·))=∫Ωf0(x,y(x),u(x))dx.
作如下假设:
最后,如果将“被”看成一个类词缀就意味着“被XX”是一个词,词最小的可以独立运用的语言单位,不能再分的。而在“被XX”结构中“被”和“XX”之间所隐匿的成分补出不会引起结构意义发生改变[13]。
(P3)f0:Ω×R×U→R满足:∀(y,u)∈R×U,f0(·,y,u)是有界可测的;∀(x,u)∈Ω×U,f0(x,·,u)∈C1(R);∀(x,y)∈Ω×R,f0(x,y,·)∈C(U).
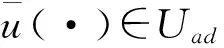
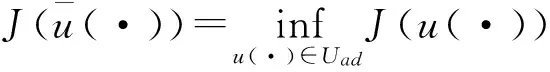
通过考虑方程(1)的正则化问题,利用变分思想给出了退化半线性椭圆方程支配系统(1)的最优对所满足的Pontryagin最大值原理.

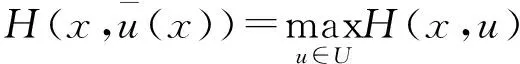
成立,其中
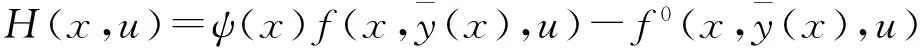
而ψ(·)∈H(Ω)满足
(2)
2 状态方程的变分
先来讨论方程(1)的正则化问题
(3)
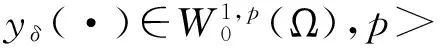

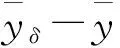
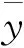
(4)
(5)
(4)与(5)式相减得
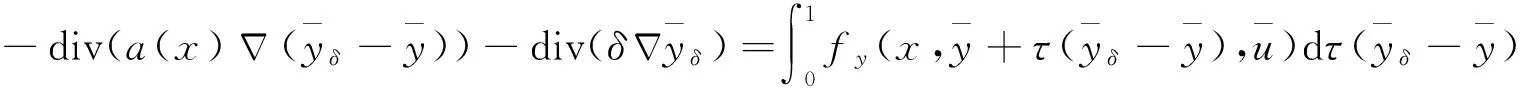
由假设(P2),上式可化为
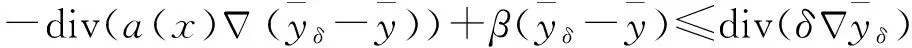
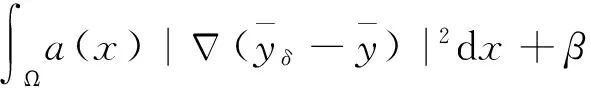
利用Cauchy不等式并整理得
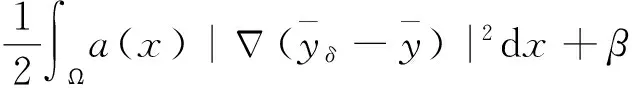
再由Young不等式有
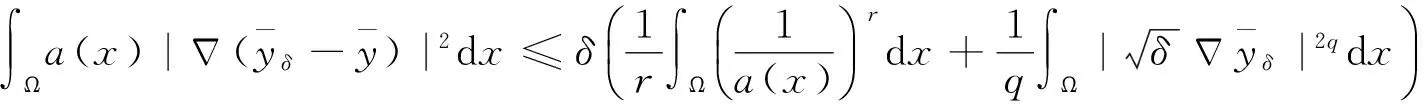
由(4)式可得
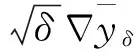
其中C1为与δ无关的常数.由椭圆方程理论[9]知
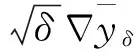
(6)
其中C2为与δ无关的常数.
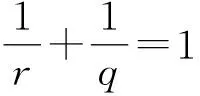
由假设(P1)及(6)式可知
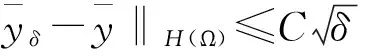
再由嵌入定理[10]知
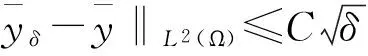
即
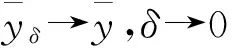
(7)

(8)
证明 ∀u(·)∈Uad,∀η∈(0,1),∃Eη⊂Ω,满足|Eη|=η|Ω|,定义
若yη(·)为方程(3)相应于uη(·)的解,则有
(9)
(9)与(4)式相减得
(10)
从而
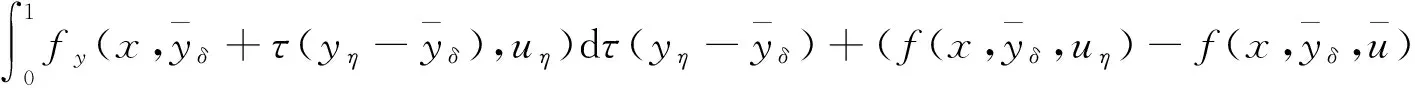
(11)
由椭圆方程解的有界性估计理论有
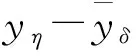
再由嵌入定理知
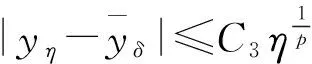
即
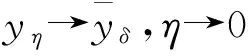
(12)
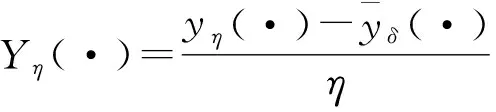
(13)
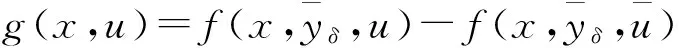
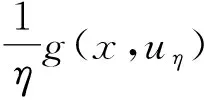
注意到
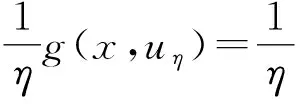
由Minkowski不等式知
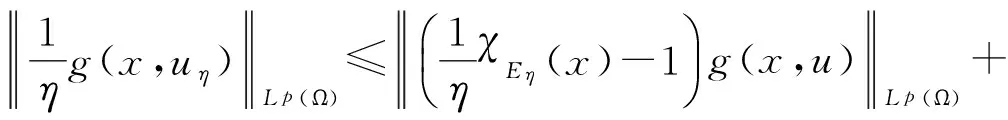
而
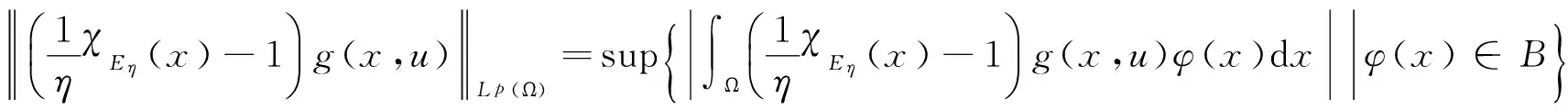
这里B为Lq(Ω)中的单位球.故∀ε>0,∃φ0(·)∈B,使得
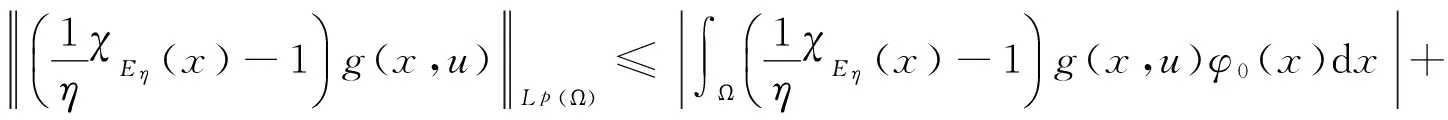
由文献[3]知,∀ε>0,∃Eη⊂Ω,满足|Eη|=η|Ω|,使得
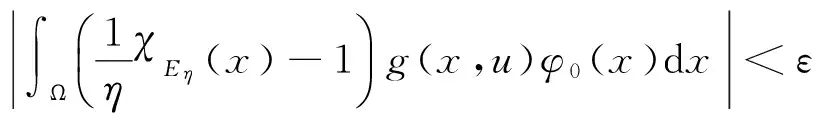
故
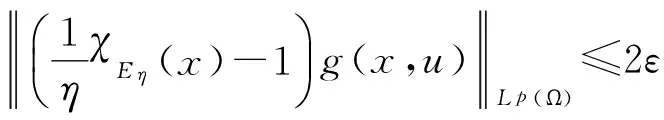
即
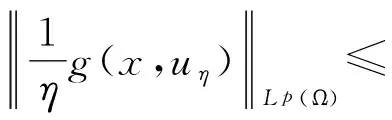
综上所述,
‖Yη‖W1,p(Ω)≤C,
再由嵌入定理知
|Yη| (14) 下面证明当η→0时,Yη(·)→Yδ(·),其中Yδ(·)满足方程 (15) 将(13)与(15)式相减得 (16) 因而 (17) 进一步有 由(12)与(14)式知 又因 由前面证明可知,∀ε>0,∃Eη⊂Ω,满足|Eη|=η|Ω|,使得 即 ‖Yη-Yδ‖W1,p(Ω)→0,η→0. 再由嵌入定理知 |Yη-Yδ|→0,η→0. 令η→0,由(13)式可知(15)式即为Yδ(·)满足的方程. 下面证明当δ→0时,Yδ(·)→Y(·),其中Y(·)满足方程(8). 将(15)式两端同乘Yδ,并在Ω上积分,利用Young不等式和假设(P2)有 (18) (19) ∀φ∈H(Ω),有 (20) 再由(19)式知,存在Y(·)∈H(Ω)和Yδ(·)的一个子列,不妨记为其本身,令δ→0有 Yδ(·)→Y(·),δ→0. (21) 且 (22) 利用(7),(20),(21)和(22)式,令η→0,δ→0,由方程(15)即得方程(8),亦称方程(8)为方程(1)的变分方程. 定理1的证明 对指标泛函作变分 令η→0,δ→0,利用假设(P3)上式化为 (23) 设变分方程(8)的对偶方程为方程(2),利用此对偶方程,(23)式可化为 再由变分方程(8)得 (24) 由(24)式可得 (25) 将(25)式除以ρ,再令ρ→0,由Lebesgue点定义得 由于H(x,u)的Lebesgue点集在Ω中稠密,因此 [1] CASAS E. Control of an elliptic problem with pointwise state constraints[J]. SIAM J Control Optim,1986,24(6):1309-1318. [2] BONNANS J F,TIBA D.Pontryagin’s pyinciple in the control of semilinear variational inequalities [J].Appl Math Optim,1991,23(2):299-312. [3] 高夯.半线性椭圆方程支配系统的最优条件[J].数学学报,2001,44(2):319-332. [4] YE YUQUAN,CHEN Q.Optimal control of the obstacle in a quasilinear semilinear variational inequalities [J].J Math Anal Appl,2004,29(4):258-272. [5] OLEINIK O A,RADKEVIC E V.Second order equations with nonnegative characteristic form [M].New York:Springer,1973,28-70. [6] CACDIROLI P,MUSINA R.On a variational degenerate elliptic problem [J].Nonlinear Differ Equ Appl,2000,7:187-199. [7] 何跃.一类二阶退化半线性椭圆型方程边值问题的适定性和解的正则性[J].数学年刊,2004,25(2):225-242. [8] 万宝成,李建,王增辉.一类拟线性椭圆型方程非平凡解的存在性[J].东北师大学报(自然科学版),2013,45(2):25-29. [9] 伍卓群,尹景学,王春朋.椭圆与抛物型方程引论 [M].北京:科学出版社,2003:199-211. [10] ADAMS R A,FOURNIER J J F.Sobolev Space[M].2nd ed.Singapore:Elsevier Pte Ltd,2003:79-101. (责任编辑:李亚军) Condition of optimal control for system governed by a class of degenerate semilinear elliptic equation ZHANG Jin1,GAO Hang2 (1.School of Science,Qiqihar University,Qiqihar 161006,China; 2.School of Mathematics and Statistics,Northeast Normal University,Changchun 130024,China) Optimal control problems for distributed parameter system governed by a class of degenerate semilinear elliptic equation are considered.When the measure of degenerate-points is zero,necessary condition for optimal control of the distributed parameter system is obtained by using regularization method and variational thought. degenerate semilinear elliptic equation;optimal control;regularization method;variational thought;maximum principle 1000-1832(2015)04-0001-06 10.16163/j.cnki.22-1123/n.2015.04.001 2014-06-30 国家自然科学基金资助项目(11071036);黑龙江省教育厅科学技术研究项目(12541891). 张敬(1969—),女,硕士,教授,主要从事控制论与偏微分方程研究;高夯(1956—),男,博士,教授,博士研究生导师,主要从事控制论与偏微分方程研究. O 232 [学科代码] 120·30 A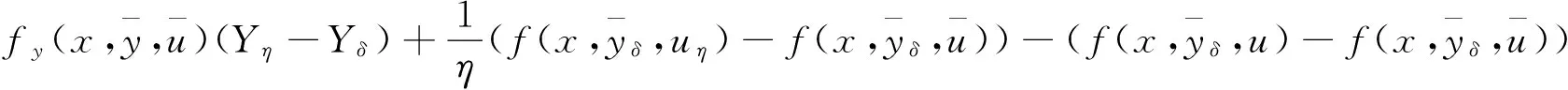
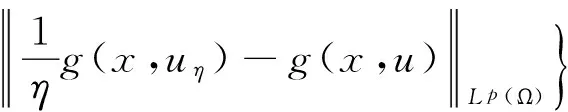
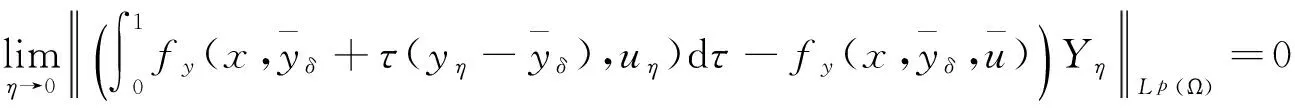
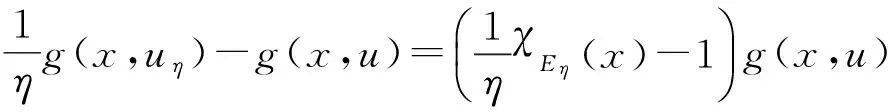
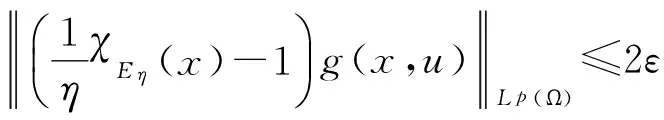
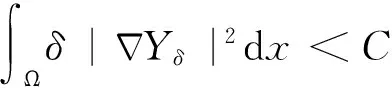
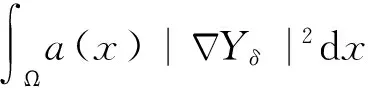
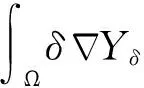
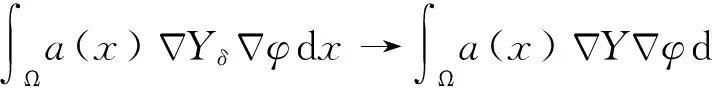
3 主要定理的证明