椭圆中的存在性成立问题

☉江苏省徐州高级中学孟文娣

椭圆中的存在性成立问题

☉江苏省徐州高级中学孟文娣

数学的深奥在于数学问题的千变万化，数学方法的灵活多变，数学思想的内在统一·函数历来是高考考查的重点，而函数中借助“恒成立”与“存在性”成立问题求解参数的取值范围又是考卷中的老面孔·很多教师致力于此类题型的研究，总结出了各种考查形式及解决方法·实际上，这类问题的本质就是化归为函数的最值问题·而在椭圆的有关问题中，椭圆离心率的求解是常考题型，特别是求离心率的取值范围是考查的重点·由于方法较多，综合性较强，这类问题往往又成为考查的难点，学生在碰到这类问题时比较棘手·笔者在执教过程中发现，在求椭圆离心率取值范围的问题中，如果能将函数中的“存在性”成立问题的思想加以借鉴，则能较快地解决一些较复杂的问题·

下面以几个较简单的例题来阐述这种思想方法的运用·

解析：此题解法较多，可通过设P点坐标，利用有界性建立不等式；也可以通过设角，转化为三角函数问题求取值范围·前者计算量较大，后者综合性较强，现在从“最值问题”研究解决方法·

通过椭圆图像不难发现，当点P在椭圆上运动时，越靠近长轴端点∠F1PF2越小，最小值趋向于0，越靠近短轴端点∠F1PF2越大，当P点与短轴端点重合时，∠F1PF2最大·即当P点在椭圆上运动时，∠F1PF2存在最大值·因此若存在点P，使∠F1PF2=90°，设短轴上的顶点为B，只需∠F1BF2≥90°即可·再利用椭圆的对称性，只需∠OBF2≥

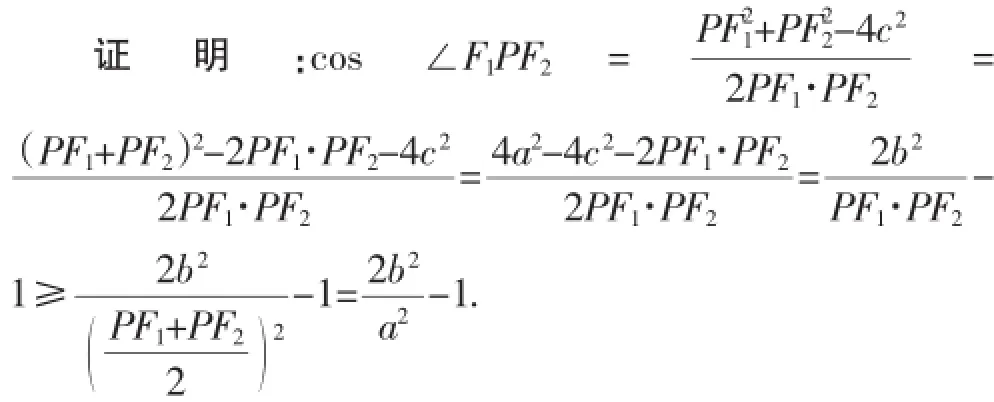
当且仅当PF1=PF2=a，P点与短轴端点重合时，余弦值取得最小值，即∠F1PF2取得最大值·

解析：此题设点坐标，利用有界性求离心率取值范围仍然是基本方法，但是运算量仍较大·点M到左焦点的距离与到右准线的距离的比值随着M的变化而变化，并且存在最值·只要2在这个变化范围内，则必存在点M满足条件·易证椭圆上的点在长轴两端点处时，到左焦点与到右准线的距离的比值取到最值·由题意，只需

（a＞b＞0）的左、右焦点分别为F1、F2，P为椭圆上任意一点·当点P在长轴右端点时，取得最小值当点P在长轴左端点时取得最大（即书上例题中出现的结论变形：椭圆上到两焦点的距离的最大值、最小值分别为a+c，a-c）

例4设点F1、F2分别是椭右焦点，若在其右准线上存在点P，使线段PF1的中垂线过点F2，求椭圆离心率的取值范围·

解析：由题意，F1F2=F2P=2c，题目转化为：存在点P，使得F2P=2c·由图易得，F2与右准线上的点的连线存在最

解析：此题虽然没有明确谈及存在性，但仔细审题不难发现，题目就是在椭圆上存在一点P，可证当点P在长轴端点时，

总结：以上各题都有其他多种解决方法，在这就不一一赘述了·椭圆中的存在性成立问题，与函数中的存在性成立问题有着异曲同工的解决方法，并且将解决函数问题的方法用到此处更显简便、自然·但是并非所有含有“存在点P”这种条件的问题都可使用这种方法，要认真审题，确定条件中所蕴含的量存在最值才能够进行转化·并且此类问题多以填空题的形式给出，如果能记住椭圆中的一些最值结论将能够大大提高解题速度·作为教师，在教学过程中要不断的摸索，真正找到数学思想、数学方法的统一，教会学生会思考，能类比，真正达到举一反三的效果·F