桥梁模态频率异常变化的概率检测方法及例证

邓 扬， 李爱群， 刘 扬

(1. 长沙理工大学土木与建筑学院， 湖南 长沙410004；2. 现代公路交通基础设施先进建养技术湖南省协同创新中心, 湖南 长沙 410004;3. 东南大学土木工程学院， 江苏 南京210096)

桥梁模态频率异常变化的概率检测方法及例证

邓 扬1, 2， 李爱群3， 刘 扬1, 2

(1. 长沙理工大学土木与建筑学院， 湖南 长沙410004；2. 现代公路交通基础设施先进建养技术湖南省协同创新中心, 湖南 长沙 410004;3. 东南大学土木工程学院， 江苏 南京210096)

针对实测模态频率的随机性，提出了基于概率统计理论的桥梁结构模态频率异常变化的检测方法。建立桥梁实测模态频率与结构温度的BP神经网络模型，进而消除温度对模态频率的影响，在此基础上采用核密度估计方法得到消除温度影响模态频率的累积分布函数，然后采用标准正态分布的逆函数将累积分布函数转换为Q统计量，最后利用Q统计量建立用于频率异常检测的均值控制图。假设检验结果表明：Q统计量服从正态分布，从而解决了消除温度影响后的模态频率仍非正态的问题，满足了控制图对随机变量正态性的要求。分析结果表明，基于控制图的概率检测方法对桥梁模态频率的异常数据具有良好的敏感性。该方法可为大跨度桥梁健康监测数据的分析与应用提供参考。

结构健康监测； 模态频率； 桥梁结构； 控制图； 核密度估计

1 概 述

多自由度结构体系的无阻尼频率方程为

(1)

式中M,K分别为质量矩阵和刚度矩阵，ω为结构频率。从式(1)可以看出，只要体系的刚度与质量不变，结构体系的频率始终为一常量。若从随机的角度看这一问题，即考虑结构体系物理、几何等参数的随机性，那么结构的动力特性(自振频率、振型等)将是服从某一分布的随机变量。目前，国内外关于随机参数结构的特征值问题已开展了大量研究[1-4]。对于已投入运营的某座桥梁，由于其物理、几何等参数已确定，因此，动力特性应保持不变，但是大量的实测数据分析表明，桥梁结构的实验模态分析数据会在某一个范围内随机变化[5-7]。导致这种变化的因素极为复杂，可能来自于环境荷载条件变化[7-9]、边界条件改变[10]、结构材料性能退化[11]以及结构损伤[12]等方面。桥梁结构模态识别的目的是为了检测出模态参数的异常变化，并以此反演和评估结构的状态，这种异常变化通常是由边界条件改变、材料劣化和构件损伤等引起，且不能自动恢复。而环境荷载条件导致的模态参数变化是可恢复的。

借鉴随机参数结构特征值问题的研究思想，可以认为在环境荷载激励下，桥梁结构的模态频率实测值也是随机变量，在此基础上采用概率统计的方法对其异常变化进行检测。首先，应尽可能消除环境荷载条件对结构频率实测值的影响。研究表明，温度、风和车辆荷载都会桥梁结构模态频率产生影响。总的来说，温度是引起桥梁模态频率实测变异性的关键因素，而风和车辆荷载对频率的影响很小[8]。因此，首先应根据长期累积的实测数据建立温度与频率的相关模型，在此基础上得到消除温度影响的桥梁结构频率。例如，Liu[13]用1年的监测数据建立了曲线预应力混凝土箱梁桥前三阶频率和温度的线性回归模型，孙君[14]采用6次多项式建立了悬索桥频率与温度的相关性模型，Moser[15]应用多种解析模型建立了一座人行天桥频率与温度的关系。由于逐渐认识到温度和桥梁频率关系的复杂性，许多学者开始尝试用人工神经网络、支持向量机等方法来分析两者之间的关系[6, 16-18]。分析表明，作为一种具有较强容错性的非线性映射工具，人工神经网络适合于建立桥梁结构模态频率与温度的相关性模型。

接下来，对频率的异常变化进行概率检测。由于测试噪声等因素的影响，消除温度影响后的频率仍存在一定的随机性。除非桥梁动力特性由于某些突发状况(地震、船撞等)发生大幅度的变化，很难从模态频率的实测值来判断结构是否异常。因此，必须从概率的角度去检测桥梁模态频率的异常变化。统计过程控制是一种借助于数理统计理论对生产过程的各个阶段进行监控以及发现异常现象的方法，控制图是统计过程控制中发展较为成熟的控制理论[19]。目前，国内外已有学者开始运用控制图对结构健康监测数据开展异常检测[14, 20-21]。由于控制图是以变量服从正态分布为前提的，因此，在采用控制图进行结构频率异常检测之前需要对频率实测数据进行正态性检验，若不服从正态分布，还需对数据进行进一步的处理。文献[14]定义了基于模态频率的润扬大桥悬索桥结构异常变化指标，在此基础上采用均值控制图对指标的异常变化进行了识别，然而并未对指标的正态性进行检验。

在已有研究成果的基础上，本文提出一种频率异常变化的概率检测方法。采用BPNN(Back Propagation Neural Networks，简称BPNN)建立频率与温度的相关性模型，继而得到消除温度影响的模态频率。针对消除温度影响后的频率不服从正态分布的情况，采用核密度估计的方法获取其概率分布函数，进而将其转换为服从标准正态分布的Q统计量，在此基础上采用均值控制图对模态频率的异常变化进行检测。最后采用这一方法对某大跨度悬索桥的模态频率实测数据进行了分析。

2 概率检测方法

2.1 频率与温度相关性模型

若正常状态下桥梁结构的某阶频率实测向量为fi(i为频率阶次)，结构温度的实测向量为T，设fi和T的长度为l。模态频率为等时间间距分析得出，然后依时间先后顺序组成频率的实测向量fi。选择频率识别的时间间距应考虑采样频率、检测时效性等各方面的因素。为增强异常检测的时效性，分析时间间距应尽量小，但是这样频率的识别结果会过于离散，影响异常检测的效果。文献[14]先识别出10 min模态频率值，在此基础上取频率日平均值与温度建立相关性模型，这样虽然减小了数据的离散性，但检测时效性不足。本文取10 min为频率识别时间间距。关于模态频率的识别方法，国内外的学者对此开展很多研究[22]，本文认为频域方法更适于快速地对现场大量的振动监测数据进行分析。

将T作为BPNN的训练输入向量，fi为网络训练的输出向量。可得正常状态下第i阶频率与温度的BPNN相关性模型

(2)

(3)

(4)

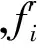
2.2 概率模型与正态化

(j,k=1, 2, …,l)

(5)

(j,k=1, 2, …,l)

(6)

(7)

式中Qi为正常状态下第i阶模态频率的Q统计向量，Ф-1( · )为标准正态分布函数的反函数。

2.3 基于正常状态的均值控制图

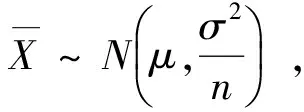
(8)

具体到向量Qi，控制图的上控制限UCL、中心线CL和下控制限LCL可以表示为

(9a)

(9b)

(9c)

式中mean(Qi)和std(Qi)分别表示Qi的均值和标准差。由于每阶模态频率的测试样本数量均为1，因此，此处n=1。

若未知状态下的频率测试向量为Ufi，对应的结构温度向量为UT，两者长度均为m。首先，将向量UT输入BPNN模型(即式(2))，得到未知状态下的频率仿真向量BPFi(UT)，再利用式(3)消除频率向量Ufi中的温度影响，即

(10)

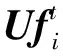
(k=1, 2, …,l；s=1, 2, …,m)

(11)

(k=1, 2, …,l；s=1, 2, …,m)

(12)

根据上述原则，选择将限流装置接入到变电站8主变的330kV出口处，限流装置的设计遵循第3小节的方法，结构采用倒置高压耦合电容器结构，主要参数如下：（1）开关型零损耗330kV电网限流装置的额定工作电流为1200A；串联电抗为2×0.6Ω；（2）智能高速开关的额定电压为12kV；额定电流为2500A；额定短路开断电流：50kA；峰值关合电流为80kA；分闸时间为 3～5ms；合闸时间为 8～18ms，反弹时间≤2ms。

(13)

式中UQi为未知状态下第i阶模态频率的Q统计向量。接下来，将UQi输入式(9)中UCL和LCL构成的均值控制图中，若向量UQi中有数据点超出控制限UCL和LCL，说明检测出了桥梁模态频率的异常变化。综上所述，图1给出了桥梁结构异常模态频率的概率检测流程。

图1 桥梁异常模态频率的概率检测流程图Fig.1 Flow chart of probabilistic detection for the abnormal modal frequencies of bridges

3 实例分析

3.1 原始数据分析

对国内某座大跨度悬索桥投入运营后动力响应的长期监测数据进行分析，共分析了一年215天的加速度响应数据，在这一年中悬索桥经历了四季的温度变化。模态频率识别采用的是最大熵谱方法[26]，得到了悬索桥主梁竖向的前7阶模态频率，由于高阶模态频率对结构损伤更为敏感，本文选取第5阶(四阶反对称竖弯振型)和第6阶(五阶对称竖弯振型)的模态频率进行分析。频率识别的时间间距为10 min，而后每6 h提取一个数据，得到860个频率原始测试值。结构温度数据来自于主梁所有温度传感器测试值的平均值，也得到了860个结构温度原始测试值，图2给出了模态频率和结构温度的原始测试数据。

图2 原始测试数据Fig.2 Original test data

实际上，由于大桥投入运营时间较短，图2中的数据都应视为来自于正常状态。为演示异常频率的概率检测方法，将图2中的原始测试数据分为两部分，其中的第301号数据至350号数据作为未知状态数据，未知状态的模态频率向量为Uf5和Uf6，结构温度向量为UT，向量长度m为50。其余的数据则组成了正常状态下的频率向量f5,f6和结构温度向量T，向量长度l为810。从图2可以看出，虽然图中模态频率的绝对变化较小，但是仍表现出显著的规律性，特别是与温度具有明显的相关性，目前，关于温度对模态频率影响规律的研究已较多[5-6, 8-9, 13-18]，本文不再赘述。

首先，图3给出了正常状态下的模态频率向量f5和f6的统计直方图，从中可以看出f5和f6表现出明显的双峰分布特点，此时，难以采用常用的概率分布模型对其进行描述，而造成这一现象的原因应是环境温度变化，因此，在进行频率异常检测之前的主要工作是通过建立频率与温度的相关性模型来消除温度对频率的影响。

图3 正常状态下模态频率原始测试值fi的统计直方图Fig.3 Histograms of original test frequencies fi in health state

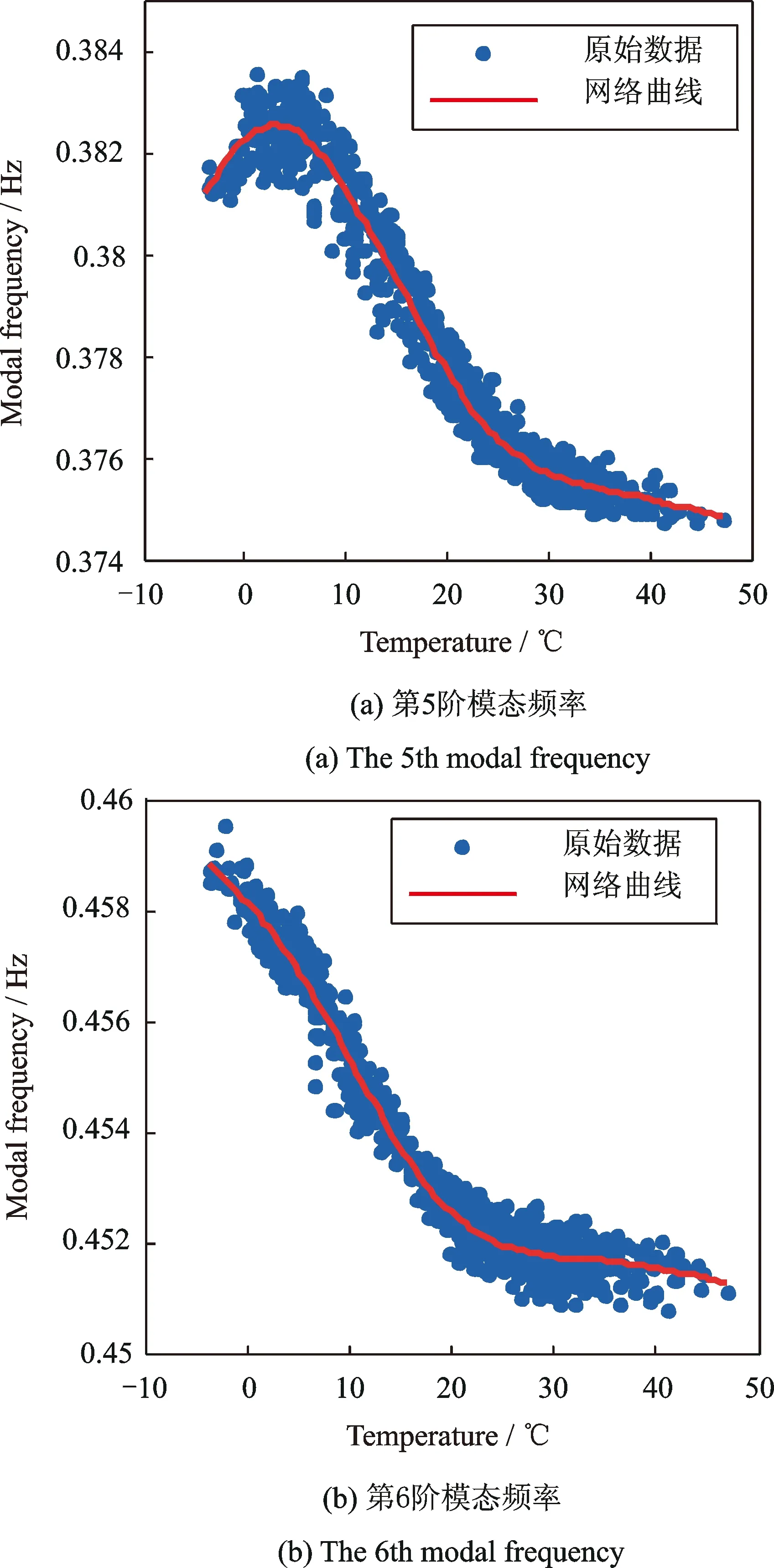
图4 正常状态下模态频率原始测试值fi与结构温度T的关系Fig.4 Correlations between original test frequencies and structural temperature in health state

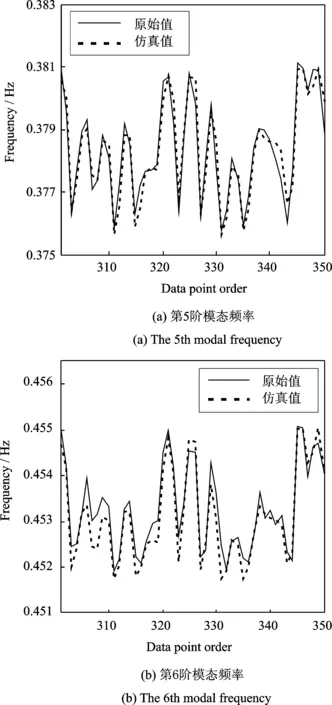
图5 未知状态下模态频率Ufi基于BPNN的仿真结果Fig.5 BPNN-based simulated results of modal frequencies Ufi in unknown state

3.2 异常检测

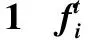
表正态分布假设检验结果

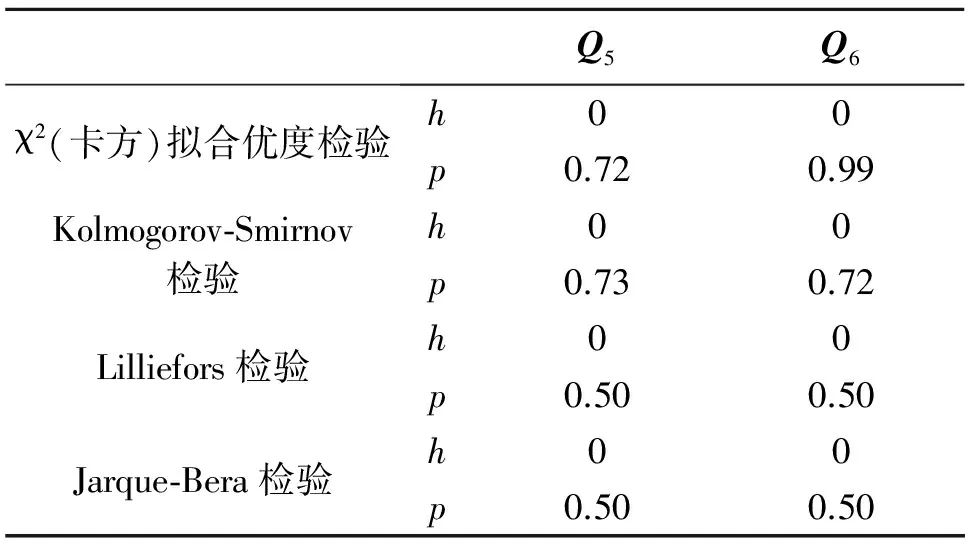
表2 Qi正态分布假设检验结果

注：表1和2中假设检验的显著性水平为0.05；表中参数h和p为假设检验结果，h=0时，认为统计量服从正态分布，h=1时，认为统计量不服从正态分布；当p大于显著性水平时，认为统计量服从正态分布，否则认为不服从正态分布。

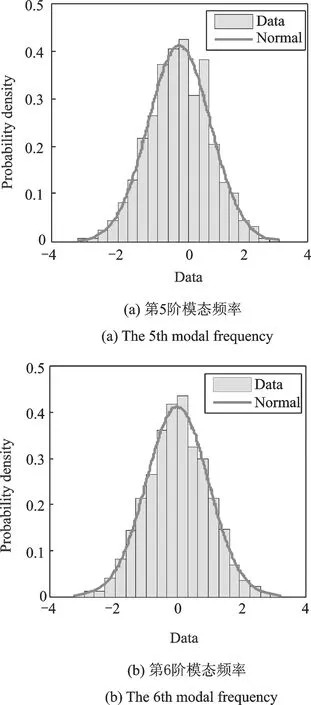
图6 正常状态下Qi的概率密度拟合结果Fig.6 PDF fitting results of Qi in health state

根据表3中Qi的均值和标准差计算控制限时，首先需要确定控制图的显著性水平α，继而找到对应的标准正态分布上α/2分位点Zα/2，在此基础上采用式(9)计算上控制限UCL和下控制限LCL。关于显著性水平，有些学者取α=0.27%[20-21]。本文认为应从避免控制图发生错误的角度去确定合适的显著性水平。第1类错误是将正常数据误判为异常数据；第2类错误是把异常数据误判为正常数据。由于本文所谓的正常状态数据和未知状态数据均来自于结构健康状态，都应视为正常数据，因此，确定显著性水平时应主要考虑避免产生第1类错误。经计算，显著性水平α=0.06%时，Zα/2=3.4，此时正常状态的Qi和未知状态的UQi均处于控制限以内，结果见图7。从图7可以看出，若本文取显著性水平α=0.27%，此时Zα/2=3，那么UCL和LCL的控制范围将大为减小，一些数据点将超出控制范围，即发生第1类错误。

表3 正常状态下模态频率的统计特性

图7 正常状态下的控制图Fig.7 The control charts in health state

第2类错误发生的概率直接反映了控制图对异常数据的敏感性，控制图越敏感，则发生第2类错误的概率就越小，控制图越不敏感，则发生第2类错误的概率就越大。通过对未知状态下的频率测试向量Ufi施加一定的变化来模拟结构的异常状态，来考察图7中的控制图对异常数据的敏感性。由于各种外界及自身不利的因素(如地震、船撞、火灾、材料劣化、锈蚀等)常常使得结构或构件刚度降低，桥梁结构的模态频率随之减小，因此，异常状态的模拟频率向量Ufi, δ为

(14)

式中δ为异常变化百分比，mean(fi)表示fi的均值，对于第5阶和第6阶模态，由表3可知，mean(fi)分别为0.378和0.453。在此基础上，同样应用式(10)～(13)将Ufi, δ转化为Q统计量UQi, δ，然后将UQi, δ输入已建立的控制限中，得到了如图8所示的异常状态下的控制图。

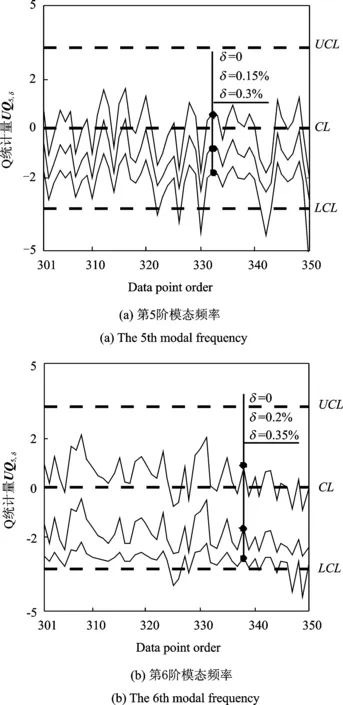
图8 异常状态下的控制图Fig.8 The control charts in abnormal state

从中可以看出，对于第5阶模态，当δ=0.15%时，Q统计量UQ5, 0.15%全部都在控制限之内，这时控制图还不能检出频率异常变化，此时认为结构仍处于正常状态，当δ增大至0.3%时，Q统计量UQ5, 0.3%有5个数据点越过下控制限LCL，说明这时控制图能检出频率的异常变化，类似的，当δ增大至0.35%时，Q统计量UQ6, 0.35%有6个数据点越过下控制限LCL。以上分析结果表明，只有当桥梁结构由于某种原因导致其模态频率的变化达到一定程度之后，均值控制图才能检出异常频率变化，而在这之前，即使模态频率发生异常变化，控制图也不能检出，这表明当频率的异常变化较小时，第2类错误是不可避免的。然而，从图8可以发现，控制图对该座悬索桥结构模态频率的异常变化具有良好的敏感性，能够成功检出结构模态频率的微小的异常变化。

4 结 论

建立了基于概率统计理论的桥梁结构模态频率异常变化的检测方法，并以国内某座悬索桥的监测数据为对象开展了分析与讨论，验证了本文方法的有效性，得到以下结论：

(1) 由于控制图理论对随机变量正态性的要求，使得频率原始测试值、消除温度影响的频率值都不能直接输入控制图中进行异常检测，本文通过核密度估计与正态化的方法有效地解决了这一问题。而控制图的结果也表明桥梁模态频率的异常变化能通过Q统计量实时反映出来。

(2) 由于环境温度变化的影响，桥梁模态频率的实测值表现出明显的双峰分布特征，不能直接采用概率的方法对其进行异常检测，需要先去除温度的影响。对消除温度影响的模态频率以及模态频率的Q统计量进行了假设检验，结果表明，消除温度影响的模态频率不服从正态分布，而模态频率的Q统计量服从正态分布。

(3) 选择该悬索桥第5阶和第6阶模态频率进行分析，模拟分析结果表明，控制图的敏感性较好，可以检出模态频率的微小异常变化，当异常变化分别达到正常状态频率均值的0.3%和0.35%时，第5阶和第6阶频率的数据点越过控制限，模态频率的异常变化被检出。

[1] 程进, 肖汝诚. 轴向荷载作用下梁结构动力特性的随机分析 [J]. 土木工程学报, 2006, 39(4): 54—57.

CHENG Jin, XIAO Rucheng. Stochastic analysis of the dynamic characteristics of beams subjected to axial loads [J]. China Civil Engineering Journal, 2006, 39(4): 54—57.

[2] 宋述芳, 吕震宙, 乔红威. 随机结构动力特征的统计矩及灵敏度分析研究 [J]. 振动工程学报, 2011, 24(2): 133—138.

SONG Shufang, LV Zhenzhou, QIAO Hongwei. Moment and sensitivity analysis for dynamic characteristic of stochastic structure [J]. Journal of Vibration Engineering, 2011, 24(2): 133—138.

[3] Kaminski M M, Szafran J. Stochastic finite element analysis and reliability of steel telecommunication towers [J]. CMES-Computer Modeling in Engineering & Sciences, 2012, 83(2): 143—167.

[4] Simoen Ellen, Moaveni Babak, Conte Joel P, et al. Uncertainty quantification in the assessment of progressive Damage in a 7-Story Full-Scale Building Slice [J]. Journal of Engineering Mechanics, 2013, 139(12): 1 818—1 830.

[5] Cornwell P, Farrar C R, Doebling S W, et al. Environmental variability of modal properties [J]. Experimental Techniques, 1999, 23(6): 45—48.

[6] 李顺龙, 李惠, 欧进萍, 等. 考虑温度和风速影响的桥梁结构模态参数分析 [J]. 土木工程学报, 2009, 42(4): 100—106.

LI Shunlong, LI Hui, OU Jinping, et al. Identification of modal parameters of bridges considering temperature and wind effects [J]. China Civil Engineering Journal, 2009, 42(4): 100—106.

[7] Zhang Q W, Fan L C, Yuan W C. Traffic-induced variability in dynamic properties of cable-stayed bridge [J]. Earthquake Engineering and Structural Dynamic, 2002, 31(11): 2 015—2 021.

[8] 邓扬, 丁幼亮, 李爱群. 环境条件影响下悬索桥模态频率变异性的定量评价 [J]. 振动与冲击, 2011, 30(8): 230—236.

DENG Yang, DING Youliang, LI Aiqun. Quantitative evaluation of variability in modal frequencies of a suspension bridge under environmental conditions [J]. Journal of Vibration and Shock, 2011, 30(8): 230—236.

[9] Hun W H, Moutinho C, Caetano E. Continuous dynamic monitoring of a lively footbridge for serviceability assessment and damage detection [J]. Mechanical Systems and Signal Processing, 2012, 33(1): 38—55.

[10]易伟建, 赵新. 持续荷载作用下钢筋锈蚀对混凝土梁工作性能的影响 [J]. 土木工程学报, 2006, 39(1): 7—12.

YI Weijian, ZHAO Xin. The effect of bar corrosion on the performance of reinforced concrete beam s under long-term load [J]. China Civil Engineering Journal, 2006, 39(1): 7—12.

[11]李枝军, 李爱群, 韩晓林. 润扬大桥悬索桥动力特性分析与实测变异性研究 [J]. 土木工程学报, 2010, 43(4): 92—98.

LI Zhijun, LI Aiqun, HAN Xiaolin. Dynamic analysis and experimental study of variations of the dynamic parameters of the Runyang suspension bridge [J]. China Civil Engineering Journal, 2010, 43(4): 92—98.

[12]蒋友宝, 刘扬, 张建仁. 钢筋混凝土拱肋破坏过程中的模态变化 [J]. 中南大学学报(自然科学版), 2012, 43(1): 338—345.

JIANG Youbao, LIU Yang, ZHANG Jianren. Modal changes in failure process for reinforced concrete arch rib [J]. Journal of Central South University (Science and Technology), 2012, 43(1): 338—345.

[13]Liu C Y, DeWolf J T, Kim J H. Development of a baseline for structural health monitoring for a curved post-tensioned concrete box-girder bridge [J]. Engineering Structures, 2009, 31(12):3 107—3 115.

[14]孙君, 李爱群, 丁幼亮, 等. 润扬大桥悬索桥模态频率-温度的季节相关性研究及其应用 [J]. 工程力学, 2009, 26(9): 50—55.

SUN Jun, LI Aiqun, DING Youliang, et al. Research on correlation of modal frequency and seasonal temperature of Runyang Suspension Bridge [J]. Engineering Mechanics, 2009, 26(9): 50—55.

[15]Moser P, Moaveni B. Environmental effects on the identified natural frequencies of the Dowling Hall Footbridge [J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2 336—2 357.

[16]Hua X G, Ni Y Q, Ko J M, et al. Modeling of temperature-frequency correlation using combined principal component analysis and support vector regression technique [J]. Journal of Computing in Civil Engineering, 2007, 21(2): 122—135.

[17]Ding Y L, Deng Y, Li A Q. Study on correlations of modal frequencies and environmental factors for a suspension bridge based on improved neural networks [J]. Science China Technological Sciences, 2010, 53(9):2 501—2 509.

[18]Zhou H F, Ni Y Q, Ko J M. Eliminating temperature effect in vibration-based structural damage detection [J]. Journal of Engineering Mechanics, 2011, 137(12): 785—796.

[19]周纪芗, 茆诗松. 质量管理统计方法[M]. 北京: 中国统计出版社, 2006

[20]王真, 程远胜. 基于受控结构振动响应的控制图损伤识别 [J]. 工程力学, 2009, 26(8): 194—200.

WANG Zhen, CHENG Yuansheng. Damage identification using time-domain response of structural under control and control charts [J]. Engineering Mechanics, 2009, 26(8): 194—200.

[21]伊廷华, 郭庆, 李宏男. 基于控制图的GPS 异常监测数据检验方法研究 [J]. 工程力学, 2013, 30(8): 133—141.

YI Tinghua, GUO Qing, LI Hongnan. The research on detection methods of GPS abnormal monitoring data based on control chart [J]. Engineering Mechanics, 2013, 30(8): 133—141.

[22]吕中亮, 杨昌棋, 安培文, 等. 多点激励模态参数识别方法研究进展 [J]. 振动与冲击, 2011, 30(1): 198—203.

LV Zhongliang, YANG Changqi, AN Peiwen, et al. Progress on modal parameter identification with multiple-excitation [J]. Journal of Vibration and Shock, 2011, 30(1): 198—203.

[23]Quesenberry C P. On properties of binomial Q charts for variables [J]. Journal of Quality Technology, 1995, 27(3):184—203.

[24]Bowman A W, Azzalini A. Applied Smoothing Techniques for Data Analysis [M]. New York: Oxford University Press, 1997.

[25]Liu R, Yang L. Kernel estimation of multivariate cumulative distribution function [J]. Journal of Nonparametric Statistics, 2008, 20(8): 661—677.

[26]李枝军, 李爱群, 韩晓林, 等. 基于最大熵谱和模糊聚类分析的斜拉桥拉索索力测试与评估 [J]. 工程力学, 2009, 26(11): 88—94.

LI Zhijun, LI Aiqun, HAN Xiaolin, et al. Measurement and estimation of the cable tension based on maximum entropy spectral and fuzzy clustering [J]. Engineering Mechanics, 2009, 26(11): 88—94.

Probabilistic detection method and its illustration for abnormal change of
bridge′s modal frequencies

DENGYang1,2,LIAi-qun3,LIUYang1,2

(1. School of Civil Engineering and Architecture, Changsha University of Science & Technology, Changsha 410004, China; 2. Hunan Co-innovation Center for Advanced Construction and Maintenance Technology of Modern Highway Infrastructure, Changsha 410004, China; 3. School of Civil Engineering, Southeast University, Nanjing 210096, China)

Due to the randomness within the measured modal frequencies, the present study develops the probabilistic detection method for abnormal change of bridge structures′ modal frequencies based on the theories of probability and statistics. The BPNN-based correlation models between modal frequencies and structural temperature are established, so as to eliminate the temperature effects in modal frequencies. Then the cumulative distribution functions of the modal frequencies after temperature effect eliminating are estimated using Kernel density estimation method. The estimated cumulative distribution functions are converted to Q statistics based on the inverse function of standard normal distribution. At last the mean value control charts of Q statistics are constructed to detect the abnormal change of modal frequencies. The hypothesis testing results show that Q statistics follow Gaussian distributions. Accordingly, the non-normality of modal frequencies with temperature effect elimination is handled to meet the requirement of random variables′ normality in control charts. The results reveal that the probabilistic detection method of control chart have good sensitivity to the abnormal data of bridge′s modal frequencies. The proposed method can provide a reference for the analysis and application of health monitoring data of long-span bridges.

structural health monitoring; modal frequency; bridge structure; control chart; kernel density estimation

2014-04-25；

2015-08-12

国家重点基础研究发展计划(973计划)(2015CB057705)；国家自然科学基金资助项目(51308073，51208067,51378081)；湖南省自然科学青年基金资助项目(14JJ3087)

U441

A

1004-4523(2015)06-0887-09

10.16385/j.cnki.issn.1004-4523.2015.06.005

邓扬(1984—), 男, 副教授。电话:(0731)85258698; E-mail:seudengyang@foxmail.com