夹支扁球壳自由振动问题的准Green函数方法

李善倾， 袁 鸿， 刘人怀

(暨南大学力学与土木工程系， 广东 广州 510632)

夹支扁球壳自由振动问题的准Green函数方法

李善倾， 袁 鸿， 刘人怀

(暨南大学力学与土木工程系， 广东 广州 510632)

将准Green函数方法应用于求解夹支任意形状底扁球壳的自由振动问题。即利用问题的基本解和边界方程构造一个准Green函数，这个函数满足了问题的齐次边界条件。采用Green公式将夹支任意形状底扁球壳自由振动问题的振型控制微分方程化为第二类Fredholm积分方程。通过边界方程的适当选择，克服了积分方程核的奇异性。最后通过离散化方程求得数值结果。数值算例表明：该方法具有较高的精度、计算量小、收敛速度快，是一种新型有效的数学方法。

夹支扁球壳； 自由振动； Green函数； 积分方程； R-函数

引 言

扁球壳的最大矢高和底面直径之比一般应小于1/5。扁球壳在土木、水利、机械、船舶、航空航天等工程中都有着广泛的应用。扁球壳作为工程结构的主要部件，在进一步的设计与研究中需考虑其动力问题，而自由振动作为扁球壳动力问题的基础应首先予以分析。 扁球壳的自由振动问题，最重要的是求固有频率，尤其是最低阶固有频率。力学工作者对小挠度扁球壳振动问题已经做了大量的研究工作，并取得了许多研究成果。本文应用准Green函数方法分析夹支任意形状底扁球壳的自由振动问题。Green函数方法广泛用来解决各种边值问题，然而，对于二维或高维问题，建立Green函数是极其复杂的，只有在极其简单的区域上(如圆、球)，可以找到Green函数,困难在于虽然易于找到满足基本方程的函数(基本解)，却难以满足问题的齐次边界条件。如果以基本解代替Green函数，将得到边界积分方程，它一般是一个在边界上具有奇异性的积分方程。针对边界积分方程存在的问题，准Green函数方法采用了另一条途径推导积分方程。应用准Green函数、边界方程及Green公式可将双调和算子方程化为积分方程。用有限元法或有限差分法求解板壳问题时，需对整个研究区域划分单元网格，前处理工作量大，数据准备麻烦，花费大量机时。边界元法则克服了区域型数值方法的缺点，只在边界上划分单元，通过基本解把域内未知量化为边界未知量来求解，使自由度数目大大减少，但这种方法却存在大量奇异积分，而且在边界及其附近区域上解的精度较低。

本文应用Rvachev[1]提出的R-函数理论和准Green函数方法，分析了夹支任意形状底扁球壳的自由振动问题。利用问题的基本解构造一个准Green函数。这个函数满足了问题的齐次边界条件，但没能满足基本微分方程，而建立准Green函数的关键在于将问题的边界用规范化方程ω=0表示出来，问题的区域由不等式ω>0表示出来。ω将存在多种选择，经过适当的数学处理，积分方程核的奇异性可以被克服。R-函数理论保证了对于任何复杂的区域，总可以找到函数ω，从而可将原问题化为无奇异性的第二类Fredholm积分方程。使用这一方法，袁鸿等已成功求解了简支及固支各向同性薄板、简支扁球壳自由振动及弯曲问题[2-7]。准Green函数方法是一种新颖的数学思想，是一种值得研究的新数值方法。与有限元法或有限差分法相比，准Green函数方法在解决的板壳问题方面，对整个研究区域划分单元网格很少，前处理工作量相对小很多，收敛速度快，计算量小，可求得很高精度的结果。本文将准Green函数方法应用于求解夹支任意形状底扁球壳的振动问题。通过夹支矩形底、梯形底扁球壳的数值结果证明了本文方法的有效性和可行性。

1 基本方程

扁球壳的自由振动微分方程组为：

▽2w(x,t)=0，x∈Ω

(1)

x∈Ω

(2)

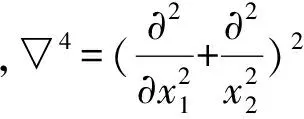
滑动夹支边界条件为

(3)

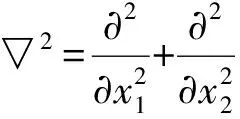
由式(1)和(3)，可得

(4)

把表达式(4)代入式(2)，可得w所单独满足的微分方程为

(5)

设

(6)

将表达式(6)代入式(5)可得夹支扁球壳的振型控制微分方程及边界条件为

x∈Ω

(7)

(8)

2 积分方程的推导

设ω=0是边界Γ的一阶规范化方程，即满足[8]：

(9)

ω(x)>0,x∈Ω

(10)

构造准Green函数如下

G(x,ξ)=-r2lnr-e(x,ξ)

(11)

e(x,ξ)=-r2lnR1+2ω(x)ω(ξ)

(12)

其中

(13)

r=(ξ1-x1)i+(ξ2-x2)j

(14)

(15)

式中 i和j分别表示x1和x2方向的单位向量，x=(x1,x2)，ξ=(ξ1,ξ2)。

显然准Green函数G(x,ξ)满足条件

(16)

(17)

为了将边值问题(7)和(8)化为积分方程，应用C4(Ω)函数类的Green公式，对所有的U，V∈C4(Ω∪Γ)有

用式(8)中的W和式(11)中的G分别代替式(18)中的U和V，并注意到(1/8π)r2lnr是双调和算子的基本解[8]，利用式(7)，(8)，(16)和(17)可得

(19)

式中

(20)

将表达式(12)代入式(20)中，进行推导，可以得到K(x,ξ)的具体表达式。

(21)

式中ω=ω(ξ)，▽=▽ξ。

当R=0时，即x=ξ，且ω=0时，表达式(21)中K(x,ξ)才可能出现不连续性。实际上，当x=ξ时，式(21)为

▽4ω-

(22)

为了使积分核K(x,ξ)∈C(Ω∪∂Ω)，将式(22)的分子1+ω▽2ω-(▽ω)2展开成ω的幂级数后，幂级数的常数项和1次项的系数必须等于0。 下面通过构造一个新的边界规范化方程来保证K(x,ξ)的连续性，为此假设

φ

(23)

式中ω0=0是边界Γ的一阶规范化方程，即满足式(9)和(10)。显然，ω=0也是一阶规范化方程。容易证明。 只要选取

(24)

就能保证K(x,ξ)在积分域内处处连续，将表达式(24)代入式(23)中，可得

(25)

因此，可以通过任意选择一个边界规范化方程ω0=0，就可以根据式(25)建立一个新的边界规范化方程ω=0，从而就可以保证积分核K(x,ξ)的连续性。

3 积分方程的离散

夹支扁球壳自由振动问题的等效积分方程(19)进行离散化。将积分域Ω划分为若干子域Ωi(i=1,2,…,N)，在各子域中分别应用中矩形公式进行数值求积。则积分方程(19)可化为齐次线性代数方程组

BN×N[W(x1) …W(xN)]T=0

(26)

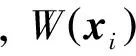
BN×N=(bij)N×N，

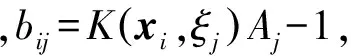
(i=1,2,…,N;j=1,2,…,N),

Aj表示第j个子域的面积。

齐次线性方程组(26)有非平凡解的条件是其系数行列式等于零，即

(27)

4 数值算例

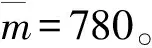
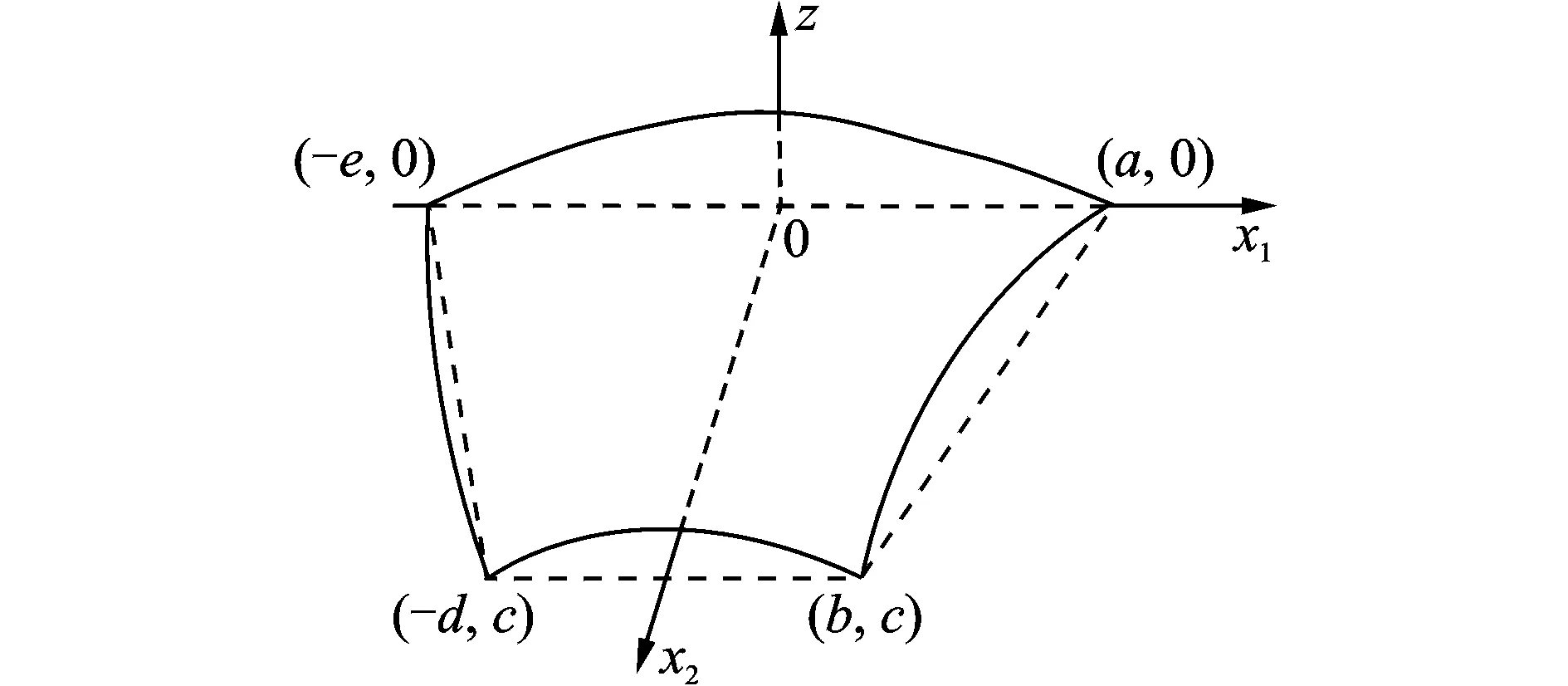
图1 夹支扁球壳Fig.1 Slip clamped shallow spherical shell

图2 矩形积分域划分Fig.2 Division of rectangular integral domain

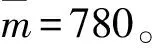
图3 梯形积分域划分Fig.3 Division of trapezoidal integral domain

表1 夹支矩形底扁球壳不同半径R值的固有频率f

Tab.1 Natural frequency f of slip clamped rectangular shallow spherical shell with different R

R模态阶数12345本文方法有限元法本文方法有限元法本文方法有限元法本文方法有限元法本文方法有限元法351．21250．33872．02871．89696．23095．494112．90111．41120．63118．15446．35945．39168．66368．52493．73892．982110．78109．27118．65116．13543．93242．90967．04766．90592．56191．795109．79108．26117．72115．18642．55541．49866．15466．00991．91591．144109．24107．71117．21114．66741．70340．62465．60965．46391．52490．750108．91107．37116．91114．35

表2 夹支梯形底扁球壳不同半径R值的固有频率f

Tab.2 Natural frequency f of slip clamped trapezoidal shallow spherical shell with different R

R模态阶数12345本文方法有限元法本文方法有限元法本文方法有限元法本文方法有限元法本文方法有限元法369．24269．08685．02085．487114．95115．92159．89160．13162．21161．41465．73465．57282．18982．674112．87113．86158．40158．64160．75159．94564．04663．88080．84481．339111．89112．89157．71157．95160．06159．25663．10962．94280．10480．604111．36112．37157．33157．57159．69158．88762．53762．37079．65580．158111．04112．05157．10157．35159．47158．65

5 结 论

本文应用R-函数理论和准Green函数方法，研究了夹支任意形状底扁球壳的自由振动问题。通过将本文方法的计算结果跟ANSYS有限元法的结果进行比较，计算量小，收敛速度快，有其优越性，表明本文方法是可行有效的、合理的。其为研究复杂边界形状扁球壳问题提供了一种新型有效的计算手段。准Green函数方法是一种新的数值方法，提高其计算精度及开拓其应用领域，有待进一步研究。R-函数理论还可用来构造满足边界条件的试函数，与Ritz法、变分法和样条函数近似法等[9-15]数值方法结合起来，有效地解决各种具有复杂边界形状的板壳力学问题。

[1] RVACHEV V L. Theory of R-function and Some of Its Application[M]. Kiev: Nauk Dumka,1982:415—421. (in Russian)

[2] 袁鸿, 李善倾, 刘人怀．Pasternak地基上简支板振动问题的准格林函数方法[J]．应用数学和力学, 2007, 28(7): 757—762.

YUAN Hong, LI Shanqing, LIU Renhuai. Green quasifunction method for vibration of simply-supported thin polygonic plates on Pasternak foundation[J]. Applied Mathematics and Mechanics, 2007, 28(7):847—853.

[3] 李善倾,袁鸿. 简支梯形底扁球壳自由振动问题的准Green函数方法[J]. 应用数学和力学,2010,31(5):602—608.

LI Shanqing, YUAN Hong. Quasi-Green’s function method for free vibration of simply-supported trapezoidal shallow spherical shell [J]. Applied Mathematics and Mechanics, 2010, 31(5): 635—642.

[4] Shanqing Li, Hong Yuan. Green quasifunction method for free vibration of simply-supported trapezoidal shallow spherical shell on Winkler foundation[J]. Acta Mechanica Solida Sinica, 2010,23 (4):370—376.

[5] 李善倾,袁鸿. Winkler地基上固支薄板自由振动问题的准Green函数方法[J]. 应用数学和力学,2011,32(3):253—262.

LI Shanqing, YUAN Hong. Quasi-Green’s function method for free vibration of clamped thin plates on Winkler foundation [J]. Applied Mathematics and Mechanics, 2011, 32(3): 265—276.

[6] 李善倾, 袁鸿, 薛兴伟. 简支梯形底扁球壳弯曲问题的准格林函数方法[J]. 计算力学学报, 2011,28(2):270—273.

LI Shanqing, YUAN Hong, XUE Xingwei. Green quasifunction method for bending problem of simply-supported trapezoidal shallow spherical shells[J]. Chinese Journal Computational Mechanics, 2011, 28(2): 270—273.

[7] Shanqing Li, Hong Yuan. Green quasifunction method for free vibration of clamped thin plates [J]. Acta Mechanica Solida Sinica, 2012, 25(1): 37—45.

[8] Ortner V N. Regularisierte faltung von distributionen. Teil 2: Eine tabelle von funda-mentallocunngen[J]. ZAMP, 1980, 31(1): 155—173.

[9] Kurpa L V, Reached V L, Ventsel E. The R-function method for the free vibration analysis of thin orthotropic plates of arbitrary shape[J]. Journal of Sound and Vibration, 2003,261(1):109—122.

[10]Kurpa L V, Lyubitska K I, Shmatko A V. Solution of vibration problems for shallow shells of arbitrary form by the R-function method[J]. Journal of Sound and Vibration, 2005, 279:1 071—1 084.

[11]Kurpa L V, Pilgun G, Amabili M. Nonlinear vibrations of shallow shells with complex boundary: R-functions method and experiments[J]. Journal of Sound and Vibration, 2007,306:580—600.

[12]Kurpa L V, Shmatko T, Timchenko G. Free vibration analysis of laminated shallow shells with complex shape using the R-functions method[J]. Composite Structures, 2010, 93(1):225—233.

[13]Breslavsky I D, Avramov K V. Nonlinear modes of cylindrical panels with complex boundaries : R-function method [J]. Meccanica, 2011,46(4): 817—832.

[14]Awrejcewicz J, Kurpa L, Osetrov A. Investigation of the stress-strain state of the laminated shallow shells by R-functions method combined with spline-approximation[J]. ZAMM, 2011, 91(6): 458—467.

[15]Pilgun G, Amabili M. Non-linear vibrations of shallow circular cylindrical panels with complex geometry: Meshless discretization with the R-functions method [J]. International Journal of Non-Linear Mechanics, 2012, 47: 137—152.

Quasi-Green′s function method for free vibration of slip clamped shallow spherical shell

LIShan-qing,YUANHong,LIURen-huai

(Department of Mechanics and Civil Engineering, Jinan University, Guangzhou 510632, China)

The quasi-Green′s function method is employed to solve the free vibration of slip clamped shallow spherical shell with arbitrary boundary shape. A Green quasi-function is established by using the fundamental solution and boundary equation of the problem. This function satisfies the homogeneous boundary condition of the problem. The mode shape differential equation of the free vibration problem of slip clamped shallow spherical shell with arbitrary boundary shape is reduced to Fredholm integral equation of the second kind by Green′s formula. Irregularity of the kernel of integral equation is overcome by choosing a suitable form of the normalized boundary equation. Finally, the numerical results can be obtained from the discretization equations. Numerical examples demonstrate that the method has high precision, small amount of calculation, and fast convergence rate, and it is a new kind of effective mathematical methods.

clamped shallow spherical shell; free vibration; Green function; integral equation; R-function

2013-05-19；

2015-06-29

国家自然科学基金重点资助项目(11032005)；国家自然科学基金青年基金资助项目(11402099)；广东省自然科学基金博士启动项目(S2013040015146)；广东省科技计划项目(2012A030200003)；广州市科技计划项目(201510010013)

O241.8

A

1004-4523(2015)06-0865-06

10.16385/j.cnki.issn.1004-4523.2015.06.002

李善倾(1982—),男,讲师。电话:15975638598；E-mail: lishanqing09@163.com

袁鸿(1963—),男,教授。电话:13660265906；E-mail: tyuanhong@jnu.edu.cn