基于多节点控制的柔性生产线缓冲容量建模与Witness仿真

宁方华, 周晓敏

(浙江理工大学机械与自控制学院先进制造技术研究所, 杭州 310018)

基于多节点控制的柔性生产线缓冲容量建模与Witness仿真

宁方华, 周晓敏

(浙江理工大学机械与自控制学院先进制造技术研究所, 杭州 310018)

适当的缓冲区容量是保证生产连续高效运行的重要条件。借鉴DBR理论,通过生产线多节点控制方法设置缓冲区容量,以提高生产线的生产效率,从而达到最优产出。以某公司柔性混流自动化生产线为研究对象,将混流生产线分解为串联生产线和并联生产线,根据不同的生产线特性分析了库存缓冲区的不同类别,建立普通、装配和装配后三种缓冲区的数学模型;同时采用Witness仿真软件对该生产系统进行动态仿真,将数学模型和仿真模型各自得出的缓冲区容量进行对比分析,给出最优缓冲区容量的建议。通过理论模型与仿真验证,结果表明,缓冲区容量的优化配置可以有效的实现生产线的平衡和生产效率的提高。

缓冲区容量; 建模; Witness仿真; 柔性生产线

0 引 言

生产线平衡率低下是很多企业都存在的问题,会产生生产成本高等问题,从而造成企业竞争能力下降。一直以来,生产线平衡问题就是生产物流研究的重点,许多学者就此进行了研究,如:何非等[1]研究过复杂装配系统的动态平衡问题;张宏林等[2]对双边多工位装配线平衡问题建立了数学模型进行求解;Chew等[3]研究了实现生产物流平衡的措施之一就是通过建立和逐步完善生产物流优化指标体系和生产计划优化体系,解决生产经营规划和生产作业计划中存在的问题。保持生产线平衡的另一重要举措是设置生产线中缓冲区,可使生产系统物流顺畅,有效缓解生产系统受异常情况的影响。

目前,传统的生产线缓冲区设置问题,主要有一般串行生产线缓冲区设置、混流生产线缓冲区设置和柔性生产线缓冲区设置。对于这几种情形的问题,已经有许多学者进行了研究。对于较为普遍的一般串行生产线,主要研究内容有基于可靠性理论建立缓冲区容量的数学模型[4-5],根据缓冲区成本最小的约束来建立数学模型并求解[6];刘明周等[7]利用瓶颈指数和瓶颈漂移指数表示瓶颈能力,求解出适应实时工况的最优生产批量和提前期,即最优缓冲;Enginarlar等[8]在确保生产速率的前提下,提出了生产线最小缓冲模型;还有Albinol等[9]直接以仿真软件模拟生产线,并分析在制品缓冲的变化情况。在混流生产线的研究上,黄波[10]提出针对瓶颈资源预先设定缓冲区的在制品上下限,从而对瓶颈资源和非瓶颈资源的工件作业调度进行控制;袁敏[11]直接引用现有公式求解在制品缓冲,然后利用仿真来修正缓冲容量。对于柔性生产线,赵晓波等[12]采用排队网络模型研究柔性制造系统重组时加工域缓冲区容量的优化配置问题;钱芝网等[13]研究了柔性生产下保持生产物流平衡的策略问题。

柔性混流生产线是目前生产制造业中应用较多的生产线类型,但是对其的缓冲区设置还没有定性或定量的解决方案。本文在分析生产线上的缓冲区类型基础上,根据柔性混流自动化生产线平衡的要求对生产线上的缓冲区进行容量设计,最终达到整个生产线效率产出最优。

1 问题的提出

某公司是一个生产瓶盖的生产型公司,瓶盖的生产线流程如图1所示,是一个柔性混流生产线,M1-M6表示各个加工机器,其中M5为装配机器。在这个生产线中,物料是以一个批量生产的方式进行加工的。每台机器的加工速度都不一样,分别为V1～V6且V1～V6是一个变化的值。如果M1和M2停工待料,将导致其他机器都处于一个等待的状态,减少了其他机器的机器使用率。对这个生产线的缓冲区进行设计,既能起到提高生产线的机器使用率,平衡生产线的作用,又不会浪费资源,进而缩短订单交货期,保证整个公司的订单交货率。针对本文生产线的特性,在生产线流程中不考虑设备成本以及其他工艺约束。

图1 生产线流程

目前对于缓冲区容量的求解还存在以下几个问题:a)许多缓冲区容量的数学模型是在一般串行生产线的基础上建立的,对于混流柔性自动化生产线的研究还未涉及;b)还未有明确的关于加工工序速度与缓冲区容量的关系模型;c)对缓冲区容量的求解主要还是在数学模型和数据统计验证的基础上进行的,还没有数学模型和仿真相结合的方法;d)对缓冲区容量求解问题都是单一的,没有考虑到不同工序前的缓冲区求解的过程是不同的。

因此,本文对于缓冲区容量的求解,首先,根据生产线各工序不同的加工状态,把生产线的工序分为三种:普通工序、装配工序和装配后工序。对应的缓冲区则可分为普通缓冲区、装配缓冲区和装配后缓冲区;其次,考虑到缓冲区容量与生产工序的可用度的关系、柔性自动化生产线中各工序生产速率的可变性,以及整体生产线的速率均衡,建立不同缓冲区的加工速度与容量的关系数学模型;最后,应用Witness仿真软件建立离散型柔性生产线仿真模型模拟实际生产线运行情况,验证数学模型得出的结果,从而得出最优的缓冲区容量。

在建立缓冲区库存数学模型之前,根据本文中生产线的特点,设定:a)缓冲区在工作时间内完全可靠,在制品运输时间忽略不计;b)Vi为工序Mi加工速度,同时也是缓冲区的物料消耗时间;c)BS为缓冲区库存量;d)Ti为Mi一次停工所需的时间;e)TMi为Mi停工间隔时间。

2 基于多点控制的缓冲区数学建模

本文在DBR理论基础上提出生产线工序多点控制方法,并且利用此方法建立缓冲区容量数学模型,进而在模型的基础上进行求解。对于本文柔性自动化生产线,因为每个工序的加工速度是变化的,同时前后工序的加工速度相互影响,因此本文不以单一的瓶颈工序来对生产线各工序进行研究,而是对生产线中各关键工序节点进行研究分析。

2.1 普通缓冲区容量的数学模型

生产线装配工序前每个机器形成一个串联系统,当工序Mi失效,缓冲区的存量耗尽的时候,生产线系统失效。本文把这类缓冲区归为普通缓冲区Bc,示意图如图2所示。

图2 普通缓冲区BC容量示意

为满足Mi+1机器的持续生产,普通缓冲区中暂存品应满足Mi+1在Mi上料时间T内的生产所需,得出缓冲库存模型BS1:

BS1>T×Vi+1

(1)

考虑工序Mi有二次上料的情况,模型必须保证第二次上料期间不会影响普通生产,所以需要对模型进行修正。为使Mi+1工序持续生产,普通缓冲区内的必须满足Mi+1工序在两次上料时间内消耗的库存,这时得出缓冲库存模型BS2为:

BS2>2T×Vi+1-TMi×(Vi-Vi+1)

(2)

从两次得出的缓冲库存中选取较大的一个作为普通缓冲区的最小缓冲库存,由公式(1)和(2)得出,最小缓冲库存的公式如下:

BSmin=max{BS1,BS2}

(3)

2.2 装配缓冲区的数学模型

对于装配工序来说,这时的生产系统是一个并联系统。装配缓冲区的示意如图3所示,两个装配缓冲区同时作用于装配工序,只有前面两道工序同时运行,装配工序才能开始运行,所以缓冲区的容量大小主要跟装配机器的加工速度和另一道并行加工机器的加工速度有关。

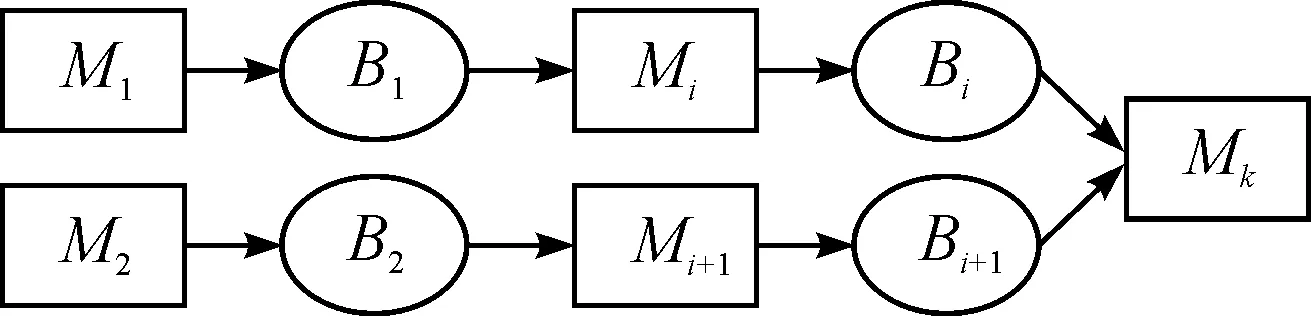
图3 装配缓冲区容量示意

在M1经过上料时间T内,Mi停止加工到开始加工的间隔时间,即Mi停工时间Ti为:

(4)

为满足装配机器的持续生产,Bi缓冲区中暂存品应满足Mk在Mi停止加工时间Ti内的生产所需,即最小库存缓冲模型为:

(5)

只有当两个装配缓冲同时满足公式(5)时,装配工序才能不停止装配。

2.3 装配后缓冲区的数学模型

装配后缓冲区运行情况与普通缓冲区和装配缓冲区的运行情况略有不同。装配后缓冲区Ba的示意如图4所示,Ba缓冲区在装配机器之后,其容量跟装配工序的加工速度有关。

图4 装配后缓冲区示意

生产线上的装配后缓冲区,其容量大小跟Mj和Mk的加工状态和加工速度有关。

a) 当Mj和Mk加工速度相差不大,在Mk停止加工的时间,缓冲区内的物料不能完全满足Mj在这段时间内的加工,这时缓冲区内的库存缓冲呈上下波动的状态,可以求出缓冲区的最小容量。

(6)

其中n表示Mk工序之前先停止加工的工序,即n=i或i+1。

为满足Mj工序在Mk停工时间内的生产所需,装配后缓冲区最小缓冲库存BS为:

BS>

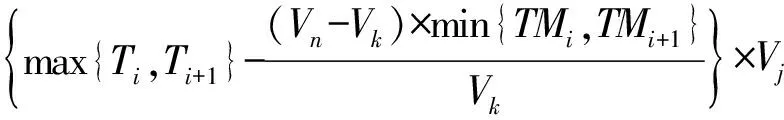
(7)

b) 当Mk和Mj加工速度相差比较大,在Mk停止加工的时间,缓冲区内的物料能完全满足Mj在这段时间内的加工,且还有剩余,这时缓冲区内的库存缓冲呈持续增长的状态,不存在最小缓冲区容量。

3 生产线的Witness仿真与模型分析

仿真技术作为一种建模方法,能够将系统的相关要素按照实际的运行逻辑有机地结合起来,真实反映出系统的行为,因此可以利用仿真模型代替解析模型研究系统的行为特性[14],而离散事件仿真技术,可以把库存、流程及设备资源等信息动态地结合起来[15]。相对于数学模型求解手段,仿真技术可以预演或再现系统的运动过程,对无法直接进行实验的系统进行仿真试验研究,从而节省大量的能源和费用[16]。

运用Witness仿真软件对生产线进行仿真建模,加入机器调整时间、参数设置时间等影响因素,得到生产线运行的仿真数据[17],可以了解生产线各工序生产速度的关系。

3.1 仿真模型的设计

本文中生产线是一个柔性自动化生产系统,所以每台机器的操作时间是有一个变化的区间的,同时M1和M2机器有一个停工待料的过程。为实现这两个功能,本文做了以下设计:

a) 为实现柔性变化的特性,对每台机器的操作时间(Duration.CycleTime)设定为V*NEGEXP(1,1)。其中V表示每台机器的操作时间的基数,NEGEXP为一个负指数函数,因此整个公式就能模拟出机器的柔性加工速率。

b)Witness仿真软件中不具备对机器直接设置上料时间的功能,同时因为柔性生产线的特性,机器每次上料间隔时间是变化的,所以为了仿真出生产线中的上料过程,将PartA,Buffer6,M1这三个元素作为一个整体,来表现出第一台机器每加工完一个批量后进行上料的过程。其中对M1的参数设置为:

General.Type: batch;

Input.Batchmin: 200;

Duration.cycletime:NEGEXP(1,1);

Setup.Mode: No. of Operations;

No.ofOperations: 60;

Opstofirstsetup: No. of Operations;

Setuptime: 10。

这里的调整时间(Setuptime)即为机器上料时间,机器加工60次所需时间就是上料间隔时间,因为每次加工时间是变化的,由此可以表示出一个变化的上料间隔时间。最后对生产系统的其他元素进行细节设计,得到生产线仿真模型如图5所示。

图5 生产线仿真模型

3.2 仿真模型的运行结果分析

实际生产线中各机器参数为:T1=10 min,V1=200 pcs/min,V2=200 pcs/min,V3=180 pcs/min,V4=175 pcs/min,V5=175 pcs/min,V6=172 pcs/min,TM1=TM2=60 min,对一天的生产过程进行模拟,生产时间为24 h,则模型运行的仿真时间为1 440 min。得到各机器的运行情况如表1所示。

3.2.1 生产线平衡分析

表1 各机器运行情况表

表1所示是各机器在生产线的各种运行情况所占的百分比。各个机器的空闲率都在5%以下,表明生产线中机器利用率高,且各机器的利用率差距小;除去上料速度,M1与M3的速度比为0.952,M2和M4的速度比为0.978 7;其他机器的速度比都约等于1,整条生产线基本达到了平衡。

3.2.2 缓冲变化曲线分析

如图6所示,坐标轴上的每条线段表示各个缓冲库存在每个时间上的实时缓冲,其中波动最大的两条曲线为B1和B2缓冲区的容量变化。另外三条曲线各自呈上下波动的状态,说明装配前工序M3和M4生产速度可以达到平衡,装配缓冲B3和B4的容量变化达到平衡,可以求出最小缓冲容量。同理可以求出装配后缓冲B5的最小缓冲容量。

图6 缓冲容量变化曲线

3.2.3 缓冲容量设计分析

仿真模型运行得出的缓冲容量数据如表2所示。缓冲区容量设计根据仿真模型运行得出的数据,同时与数学模型计算出的理论容量进行对比分析。由表2可知,机器1后的缓冲区B1的现时缓冲最大值为1 380 pcs,所以由仿真模型得出的B1缓冲库存应不小于1 380 pcs;由公式(3)得出B1缓冲容量等于2 400 pcs。当B1缓冲容量为1 380 pcs时,M3机器有4.55%的空闲时间,缓冲容量应该大于仿真模型得出的缓冲容量。所以B1容量应该设为2 400 pcs;同理设置B2缓冲区容量为2 000 pcs。

表2 现时库存的数据统计

装配缓冲B3和B4相互联系,只有两个缓冲区同时达到理论缓冲库存,才能保证装配工序100%运行。M3后的缓冲区B3的现时缓冲最大值为570 pcs,由公式(5)得到B3最小缓冲BS=583 pcs,实际生产线上的缓冲库存小于理论缓冲,则会导致另一装配缓冲B4的实际缓冲大于理论缓冲,则由公式(5)得出B4的理论缓冲250 pcs小于实际缓冲262 pcs是合理的。所以设置B3最小缓冲为583 pcs,B4最小缓冲为250 pcs。

仿真模型得出B5缓冲区容量为334 pcs,由公式(7)得出理论缓冲为245 pcs。由表1可知M5和M6没有完全的平衡,则其误差是合理的。所以设置B5缓冲区缓冲为245 pcs。

最终缓冲容量设计如表3所示。

表3 缓冲区容量设置

4 总 结

在DBR理论基础上,本文提出了多节点控制的缓冲区容量设置方法,设计了不同节点上的缓冲区容量模型和Witness仿真模型,并引入了实际生产线数据加以求解验证,得到了以下结论:a)处于不同节点上的缓冲区容量差异较大,需要分别建模求解;b)由仿真结果显示,当生产线各工序利用率95%以上,各工序机器的速度比都约等于1的时候,各缓冲区容量变化曲线收敛,可以求出最小缓冲库存容量;c)仿真模型得出的最小缓冲库存容量与数学模型得出的缓冲容量趋于一致。因此,缓冲区容量的优化配置可以有效的实现生产线的平衡和生产效率的提高。

[1] 何 非, 饶运清, 邵新宇. 基于装配关系复杂性的装配线动态平衡问题[J]. 计算机集成制造系统, 2013, 19(1): 29-38.

[2] 张宏林, 殷复鹏, 吴爱华. 双边多工位装配线平衡问题[J]. 计算机集成制造系统, 2013, 19(2): 421-428.

[3] Chew E P, Tang L C. Warehouse-retailer system with stochastic demands: non-identical retailer case[J]. European Journal of Operational Research, 1995, 82(1): 98-110.

[4] 周海荣, 王少华, 张 令, 等. 基于可靠性的连续生产在制品库存的建模分析[J]. 机床与液压, 2011, 39(9): 111-113.

[5] 孟吉伟, 王少华, 李小龙. 串行连续生产线的缓冲库存控制与可靠性研究[J]. 机械设计与制造, 2012(5): 6-8.

[6] 谭 民. 缓冲区容量的优化分配[J]. 控制与决策, 1992, 7(5): 386-389.

[7] 刘明周, 凌 琳, 唐 娟. 基于漂移瓶颈的制造车间生产批量提前期研究[J]. 中国机械工程, 2013, 24(2): 220-225.

[8] Enginarlar E, Li J, Meerkov S M, et al. Buffer capacity for accommodating machine downtime in serial production lines[J]. International Journal of Production Research, 2002, 40(3): 601-624.

[9] Albino V, Dassisti M, Okogbaa O G. Approximation approach for the performance analysis of production lines under a kanban discipline[J]. International Journal of Production Economics, 1995, 40(2): 197-207.

[10] 黄 波. 混流制造车间的生产物流优化关键问题研究[D]. 重庆: 重庆大学, 2012: 45-47.

[11] 袁 敏. 托辊生产线物流系统的建模与仿真[D]. 上海: 上海交通大学, 2013: 60-62.

[12] 赵晓波, 张 鸣, 罗振壁, 等. 可重组FMS中缓冲区容量的优化配置问题[J]. 系统工程学报, 2000, 15(2): 158-162.

[13] 钱芝网, 王晓光, 张 李. 基于柔性生产的生产物流平衡策略研究[J]. 工业工程与管理, 2012, 17(2): 13-20.

[14] 王国新, 宁汝新, 王爱民, 等. 仿真优化在制造系统中的应用现状及发展趋势[J]. 系统仿真学报, 2008, 20(1): 1-6.

[15] 赵 宁, 杜彦华, 董绍华, 等. 基于循环仿真的钢铁板坯库天车作业优化[J]. 系统工程理论与实践, 2012, 32(12): 2825-2830.

[16] 王亚超, 马汉武. 生产物流系统建模与仿真: Witness系统与应用[M]. 北京: 科学出版社, 2006: 3-4.

[17] 茅娴莘. 基于Witness仿真的TiW蚀刻机台产能改善研究[D]. 上海: 上海交通大学, 2011: 50-51.

(责任编辑： 康 锋)

Buffer Capacity Modeling and Witness Simulation of Flexible Production Line Based on Multi-node Control

NINGFang-hua,ZHOUXiao-min

(Institute of Advanced Manufacturing Technology, School of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Appropriate buffer capacity is an important condition to ensure the efficient and continuous operation of the production. Referring to the theory of DBR, this paper sets buffer capacity through multi-node control of production line to improve production efficiency of production line so as to reach the optimal output. This paper takes automatic production line of flexible mixed flow of a company as the object of study, decomposes mixed flow production line into serial and parallel production lines, analyzes different categories of the stock buffer in accordance with different production line characteristics and establishes three mathematical models of common, assembly, and after-assembly buffer zones. Meanwhile, Witness software is used to carry out dynamic simulation of the production system. In addition, this paper also conducts contrastive analysis of buffer capacity gained by mathematical models and simulation model. Finally, the suggestion on the optimal buffer capacity is given. The results of theoretical models and simulation proof show optimal configuration of buffer capacity can effectively achieve production line balance and production efficiency improvement.

Buffer capacity; modeling; witness simulation; flexible production line

1673- 3851 (2015) 01- 0062- 05

2014-03-05

宁方华(1978-),女,山东泰安人,博士,副教授,主要从事物流与供应链管理、生产系统建模与仿真方面的研究。

TB491

A