激波加载单双圆柱非稳态曳力的数值研究

陈婉君, 章利特, 施红辉, 郝李娜, 黄保乾

(浙江理工大学机械与自动控制学院, 杭州 310018)

激波加载单双圆柱非稳态曳力的数值研究

陈婉君, 章利特, 施红辉, 郝李娜, 黄保乾

(浙江理工大学机械与自动控制学院, 杭州 310018)

采用Fluent软件对激波诱导单双圆柱模型绕流场进行二维数值计算,深入研究马赫数为1.14的激波与直径为40 mm的单、双圆柱模型相互作用时绕柱流场的非稳态曳力的形成机理。结果表明:单、双柱模型(H=1.5)的曳力系数Cd曲线都存在明显的波峰和多个波谷结构,并以波幅不断减小的方式逐渐趋于某个稳定正值,其中波峰峰值远大于稳态值;相比于单柱情形,由于双柱空间位置的限制,使得环绕每柱的激波结构可以发生相互干涉,从而影响了环绕圆柱的压力以及剪切应力分布,导致单双柱曳力系数曲线波动变化的差异。

激波; 单/双柱; 非稳态曳力; 曳力系数; 相互干涉

0 引 言

激波加载固体颗粒群的问题是超音速气固两相流中的重要研究课题之一,掌握激波与颗粒相互作用机理对工业生产和生活至关重要,医学界开展的无针注射[1-2]和工业上的超音速冷喷涂[3]都是基于此机理的实际应用。国内外学者针对单颗粒相互作用进行了大量的研究和数值研究,Saito等[4]对气体—颗粒混合物中非稳定曳力对激波后流场非平衡流场结构的影响开展数值研究,发现较低的激波马赫数和较高的颗粒质量比对阻力系数时间依赖效应的影响更大;Dan等[5]对激波与单颗粒相互作用的数值研究表明,模型球所受的阻力主要由作用于其表面的流体粘性剪切力和压力共同决定,马赫数和颗粒直径的减小都导致颗粒阻力系数的增大;Tanno等[6]利用安装传感器直接测量激波作用在小球上的加速度,获得与数值模拟结果相当吻合的激波加载模型球的非稳态曳力,同时应用高速摄影仪和双曝光全系干涉仪共同揭示了在压力测量和阻力测量中个别波的相互作用。上述研究一般都只着重于激波与单球的相互作用,未考虑在多个模型球的情况下,激波结构会发生相互干涉,以至于会出现区别于单球情形的流场结构。

由于圆柱与圆球在对称截面上形状一致,所受阻力(曳力)与壁面压力、剪切应力关系类似,考虑到本文采用Fluent软件进行流场数值模拟时,三维计算的网格数目和计算时间超出了承受范围,而二维圆柱绕流计算并不妨碍激波结构干涉对非稳态曳力影响机制的揭示,因此本文的数值模拟基于二维进行。本文利用Fluent软件对单双柱绕流场进行模拟,获得激波与单双柱相互作用时的曳力系数曲线以及圆柱周围流场的压强,圆柱壁面压力和剪切应力分布等物理特性,以圆柱所受的压力和剪切应力为着重点深入分析绕柱流场的变化对曳力系数曲线波动的影响机制,以及单柱与双柱曳力系数Cd曲线差异的产生原因。

1 二维计算模型与计算方法

1.1 控制方程

本文数值模拟的对象是激波管装置内激波诱导的单、双柱绕流场,属于非定常可压缩粘性流动。该流动可用笛卡尔坐标系下的N-S方程描述:

连续方程:

(1)

动量方程:

(2)

能量方程:

(3)

其中,

(4)

这里τij为粘性应力张量，ρ为密度,ui为速度分量,P为压力,E为单位质量流体的内能,κ为热传导系数,T为温度,μ为动力粘性,μT为涡旋粘性系数。

波前气流和波后气流均可视为理想流体,以柱直径和波后气流为特征参数定义的流动雷诺数为209300,为湍流流动,故采用理想气体状态方程和可实现k-ε湍流模型来封闭控制方程。

1.2 二维计算模型及计算参数

二维计算模型如图1所示,利用Gambit建立单柱的2D数值计算模型,选取1.2 m×0.2 m的计算区域,模型柱直径为0.04 m,采用结构化网格划分求解区域,计算网格数设为238793和237278。流动通量类型选择Roe-FDS,通过patch实现波后气流的压力、速度和温度。表1显示了依据激波管理论确定的单、双柱绕流计算参数,其中,无量纲间距H定义为双柱的柱心间距与柱直径之比,本文双柱模型取H=1.5,即双柱的中心距离为0.06 m。声速取22℃温度下的对应值约为344.37 m/s。

图1 单柱模型计算区域

激波速度VS/(m/s)激波马赫数MS波后气流速度v2/(m/s)波后气流压力P2/Pa波后气流温度T2/K波后气流密度ρ2/(kg/m3)3941．1477136741321．791．48

1.3 有效阻力系数计算

文献[5]对激波与单颗粒相互作用的数值研究表明,模型球所受的曳力主要由作用于其表面的流体粘性剪切力和压力共同决定。壁面压力与剪切应力跟曳力离散关系如图2所示,通过对圆柱壁面进行受力分析,可求得非稳态力矢量FD与壁面压力和剪切应力的积分关系,可由式(5)表示:

FD=∮(-p)cos(n,τ)dζ+∮(σ)csc(τ,i)dζ

(5)

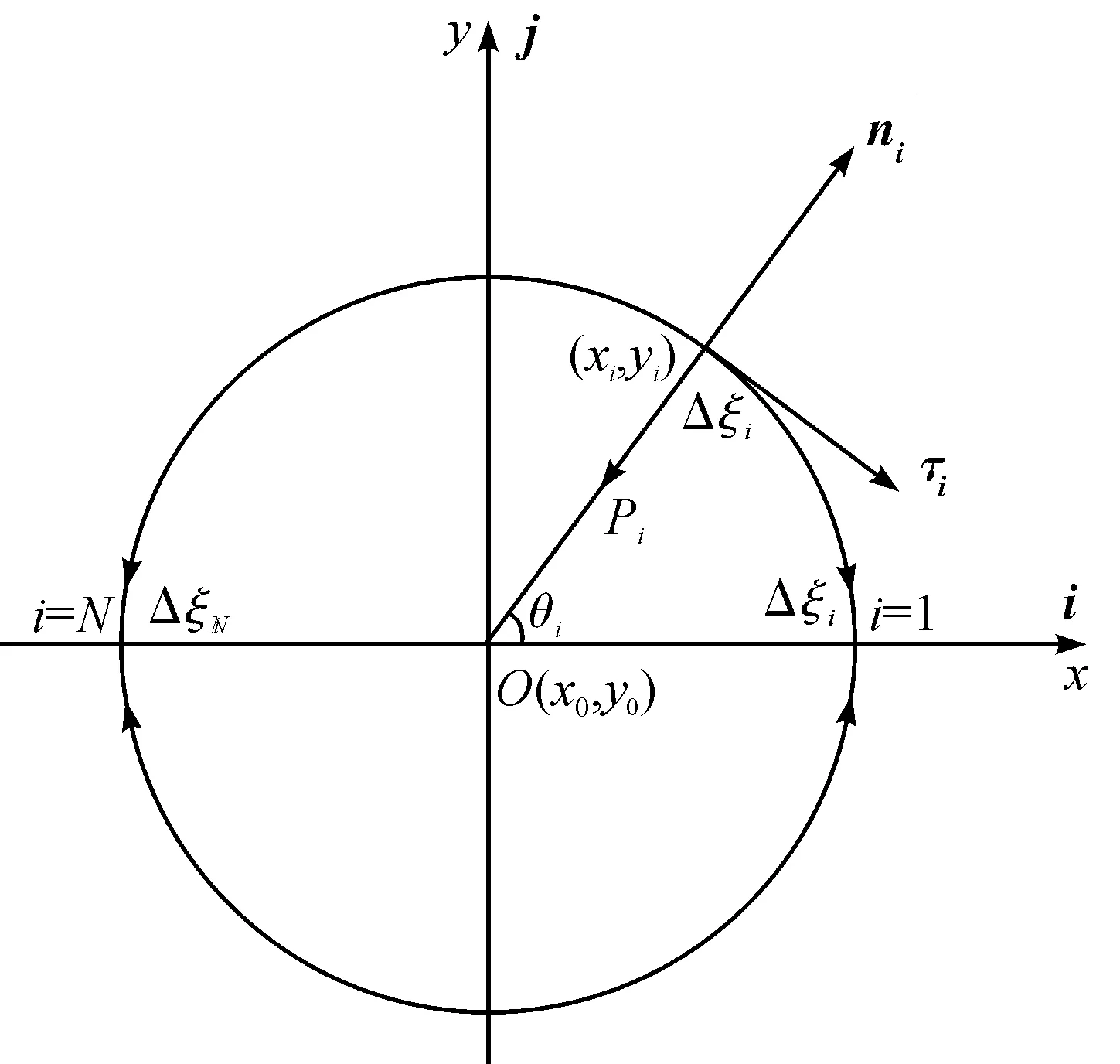
图2 壁面压力与剪切应力跟曳力离散关系

本文研究的曳力指该力矢量在激波管轴向的分量FD,数值计算时,需对积分关系式(5)的右端各项离散得到关系式(6),并沿x轴投影来确定FD,再依据曳力系数公式确定Cd。

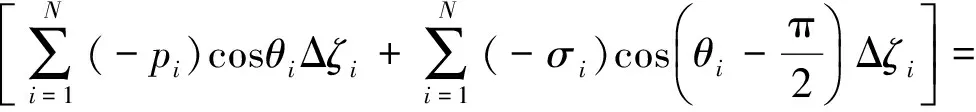
(6)

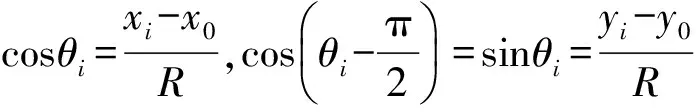
(7)

其中F为总的力矢量,由两个环面积分的矢量和决定;P是壁面压力;n是外法向单位矢量;S是柱面面积;σ是壁面剪切应力;τ是切向单位矢量(决定剪切应力在切面上的指向);i是x轴方向单位矢量;FD为曳力;Fx为矢量F在x轴上的投影;两个余弦函数为方向余弦,分别是外法向单位矢量与x轴正向的余弦值,以及切向单位矢量与x轴正向的余弦值。

曳力系数公式为:

(8)

其中,ρ2和v2分别为激波后气流密度和速度,π为圆周率,r为圆柱半径。

1.4 流场计算准确性验证

图3和图4分别显示了不同时刻沿激波管轴线的压力、相同时刻的速度分布和密度分布。根据图3计算可知激波速度约为400 m/s,对应激波马赫数为1.16。波后气流的速度、压力和密度分别为75.3～77.6 m/s、136 704～137 762 Pa和1.48～1.49 kg/m3。由于管壁和流体粘性的影响,波后气流速度、压力和密度等参数并非均匀值,而是分布在上述范围内。与表1激波管理论所确定的参数相比,激波速度或者激波马赫数的相对误差仅为1.5%,且激波管理论值都包含在上述的分布范围内。综上所述,可以验证本文数值模拟计算模型和方法的准确性。

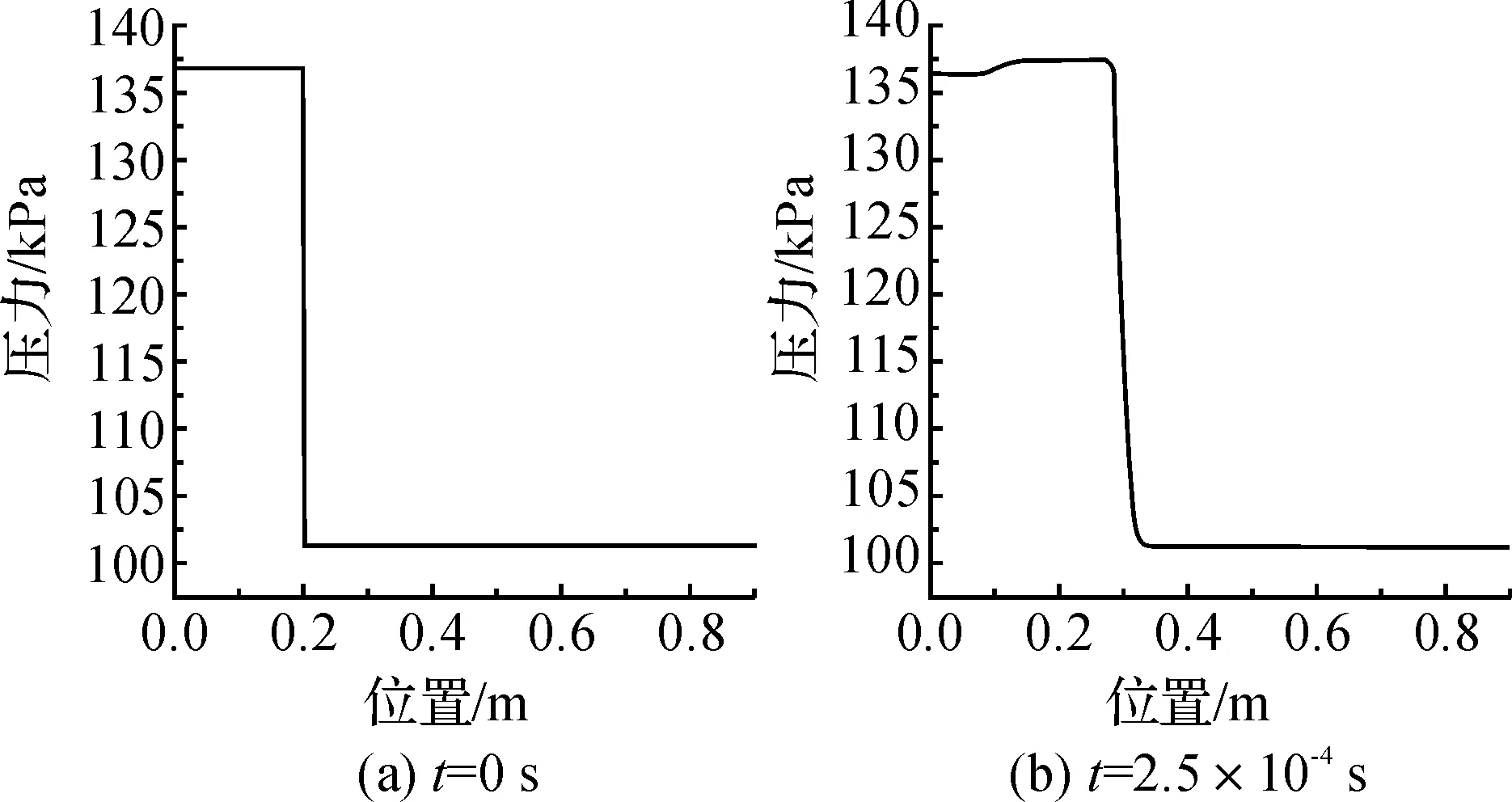
图3 不同时刻激波管轴线压力分布

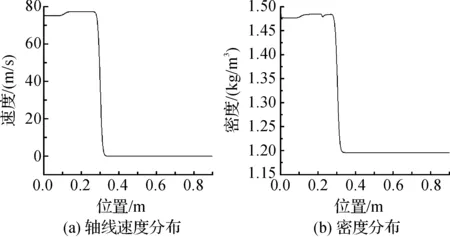
图4 t=2.5×10-4 s时刻激波管轴线速度分布和密度分布

2 单双柱模型数值计算结果及分析

图5为直径D=40 mm、Ms=1.14时的单双圆柱曳力系数Cd与无量纲时间t′的关系。表2为单双柱模型曳力系数曲线的波峰值和波谷值。从图5中可以发现单、双柱模型非稳态曳力系数曲线的趋势基本一致,随着无量纲时间t′(定义为圆柱直径与激波速度之比,下文简称时间)的增大,曳力系数曲线先急剧上升,达到第一波峰后急剧下降,再先后出现第一负值波谷、第二波峰、第二负值波谷,继而波幅逐渐减小,逐渐趋向相对于峰值很小的稳定正值。通过图5和表2可以发现两者曳力系数曲线存在一些显著差异,a)双柱(H=1.5)最大峰值Cd高于单柱相应值,且双柱的第一波峰出现的时刻t′=3/4较单柱时的t′=1/2要晚;b)双柱第二波峰的峰值比单柱相应值要高;c)双柱曳力系数曲线波动变化持续时间更长,更难以趋于稳态正值。

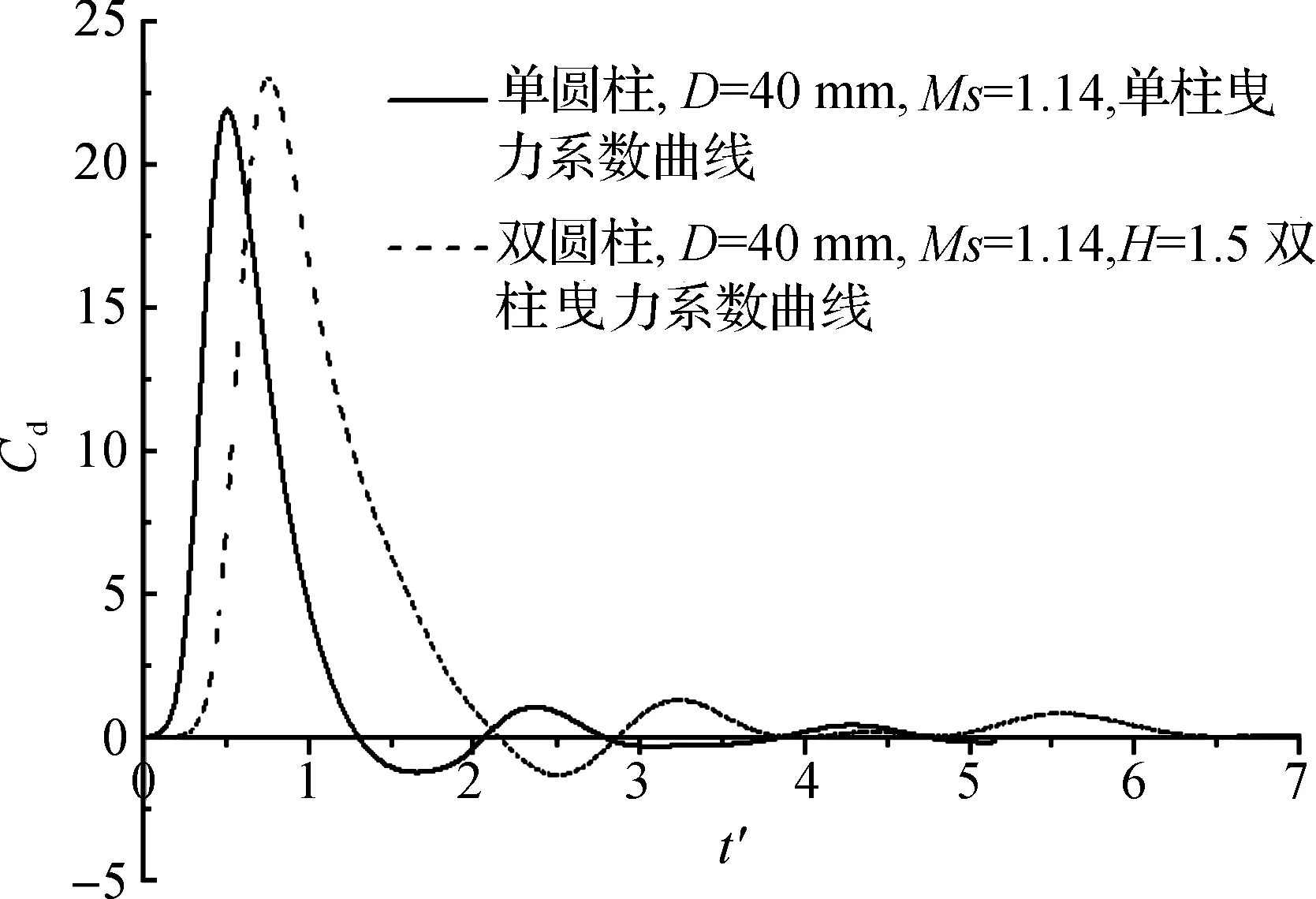
图5 单、双圆柱曳力系数与无量纲时间的关系

类型激波马赫数Ms第一波峰位置t′峰值Cd第一波谷位置t′谷值Cd第二波峰位置t′峰值Cd第二波谷位置t′谷值Cd单柱1．140．521．931．65-1．22．371．073．07-0．3双柱1．140．7523．042．51-1．33．241．333．950．006

图6为直径D=40 mm、激波马赫数Ms=1.14条件下,无量纲时间t′=0～2期间单柱周围的压力分布。图7为相应时刻的圆柱壁面压力和剪切应力分布。由于上、下参数分布几乎完全重叠,因此,都只给出上半柱模拟结果。为了更好地解释非稳态曳力系数曲线形成机理,在此作出以下四点说明:其一,t′=0是根据曳力系数上升沿起点确定的,由于这个时间很短,所以很可能会有点偏差;其二,由于激波马赫数较小,激波达到圆柱壁面前由于柱面影响,靠近轴线的激波阵面中心区域向上游方向发生一定程度弯曲,所以激波阵面中心区到达前驻点时,其前缘已越过前驻点一段距离;其三,由于Fluent在求解粘性流动时,对激波阵面的分辨能力有限,所以激波阵面呈现图6所示的压力条带状连续变化的情形。其四,如图7(b)所示,在t′=0～2时间范围内,由于壁面的剪切应力数值非常小,在激波与圆柱相互作用时间这一很小的时间量级里,剪切应力只对曳力系数曲线的细节变化会有影响,不能改变基本走势,对曳力仅产生次要影响,可忽略不计,但随着时间的增长,进入稳态阶段后,最终会占据统治地位,使曳力处于稳定的状态。

图6(a)对应于t′=0时刻,发现此时的激波阵面已经越过前驻点些许距离,其下游区域依然保持初始压力,而在前驻点出现非常集中的高压区。此时壁面的压力分布情形为:从前驻点往后压力持续减小,降到80°(注:0°、90°和180°分别对应于前驻点、赤道和后驻点)以后压力几乎没有受到激波任何影响(见图7(a)的t′=0时刻壁面压力分布曲线)。由于此时赤道左半部分的壁面压力对曳力的贡献全部为正,导致曳力由0急剧增大。t′=1/4时刻,激波阵面分布在45～90°之间,前驻点附近的高压区域与壁面的接触范围进一步扩展,且壁面压力值相对于t′=0时刻显著增大,即保持了曳力系数曲线大斜率上升的趋势。

图6 D=40 mm、Ms=1.14时,单柱周围的压力分布(激波从左往右传播)

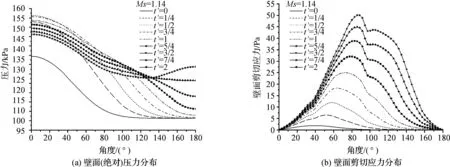
图7 不同时刻单柱壁面压力和剪切应力分布

图6(c)对应于t′=1/2时刻,激波阵面分布在赤道两侧约70～110°范围,前驻点附近的高压区域继续扩大,此时压力影响范围扩展到约120°位置(见图7(a)),在0～90°范围内的各点处压力相对于t′=1/4时刻都显著升高,且在0～30°范围分布的压力值相对于其他任意时刻都高。观察图6(d)对应于t′=3/4时刻可以发现其压力作用范围已超过150°,且90～150°分布的压力比t′=1/2时刻在各点分布的压力都高,由曳力积分关系式(1)可知,分布在0～45°范围的压力贡献为正,且较45～90°范围的压力影响更大,而在90～180°的贡献为负。因此,在t′=1/2时刻附近出现了曳力(系数)的最大值,对应了图3中的曳力系数曲线波峰位置,而且此后到t′=2之间的各时刻柱面在90°～180°范围的压力分布对曳力呈负值贡献,所以曳力系数曲线呈现持续下降变化。

在t′=1/2之后,由于从前驻点侧反射的激波向外传播,影响范围不断向外蔓延,而赤道左壁面压力却呈现下降趋势(见图7(a)),这对曳力在t′=1/2之后的下降具有重要影响。在t′=1/2～1期间,激波阵面压力分布范围逐渐覆盖赤道右半区,但右半区的压力却没有显著升高(见图7(a)),这是由于激波在跨越赤道后的沿壁面发生衍射,激波强度随角度的增大不断下降。在t′=1到t′=5/4之间的某时刻开始,衍射波在后驻点附近聚集,使局部压力急剧升高,影响范围也逐渐扩展,由于从赤道后不同位置发出的衍射波强度和速度不尽相同,因此到达后驻点形成的聚焦行为可能持续出现。又由于后驻点附近的急剧升高的聚焦压力对曳力的贡献为负,所以后驻点激波聚焦发生时,曳力系数曲线出现波谷,甚至是负值,而且可能多次出现(见图5)。

图8为D=40 mm、Ms=1.14、H=1.5时双柱周围的压力分布,图9为双柱上、下侧壁面的压力分布。t′=0时刻,双柱的上、下两侧激波阵面基本对称,与单柱情形一致。但从t′=1/4时刻开始,由于双柱相对空间位置对彼此激波结构的限制作用,双柱的压力分布表现出与单柱的差异,激波阵面在双柱之间出现扭曲,每柱上、下侧的压力分布不对称性随时间的延长也逐渐显现。

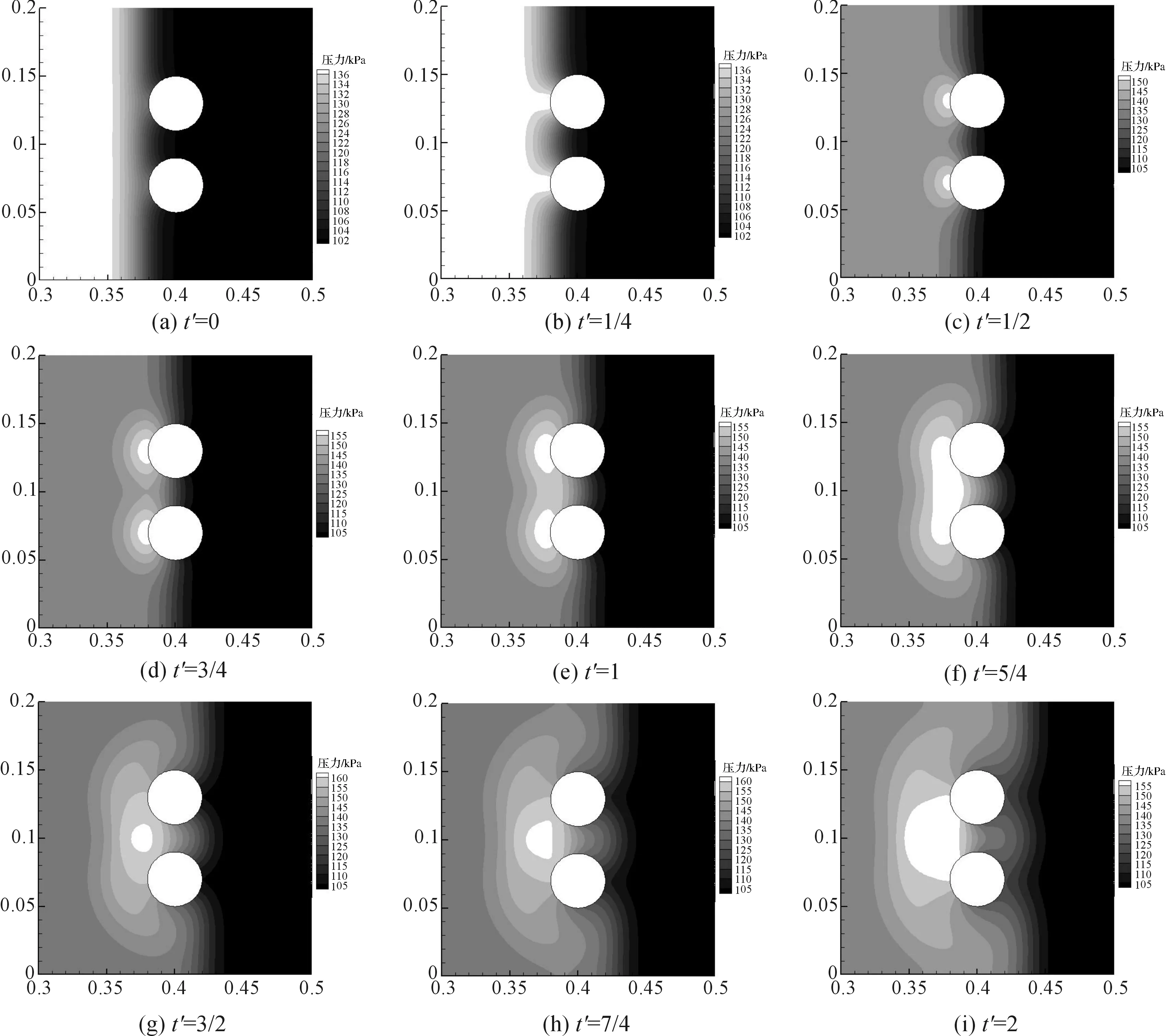
图8 D=40 mm、Ms=1.144时,双柱周围的压力分布(激波从左往右传播)

由图8(c)对应的t′=1/2和之后各时刻压力分布可以发现,入射激波被前驻点附近壁面反射后,以各自前驻点为中心向外辐射发展,各自影响范围逐渐扩大,这与单柱情形相同,并且在t′=1/2至t′=3/4之中某时刻起双柱的反射激波在双柱中心处相遇,开始发生相互干涉。在t′=1时刻,双柱对称中心线与双柱前驻点连线的焦点附近出现高压区域,称之为干涉区。在t′=5/4时刻,各柱的反射激波影响范围和干涉区都显著扩展,干涉区内的压力值进一步提升。从t′=7/4时刻开始,尽管反射激波的影响范围继续扩大,但压力值呈现明显下降,且维持高压力值,这是由于从双柱内侧壁面不断反射的激波向上游方向和对方柱面传播,导致其强度和传播方向都会有相应的改变,从而引起高压干涉区的持续存在和发展。此外,干涉区的外层内也保持较高压力水平,在靠近柱面部分形成尖角结构,并朝对侧柱面不断发展,相信在t′>2之后较短时间内,终将到达柱面,势必引起赤道左半区内侧柱面压力的显著升高。除了反射激波的干涉外,从赤道右半区内侧壁面不同位置处发出的衍射波同样也会发生干涉,使得双柱间激波阵面前缘形状从凹变凸,势必改变衍射波的强度、速度和衍射波干涉区域内的压力分布。

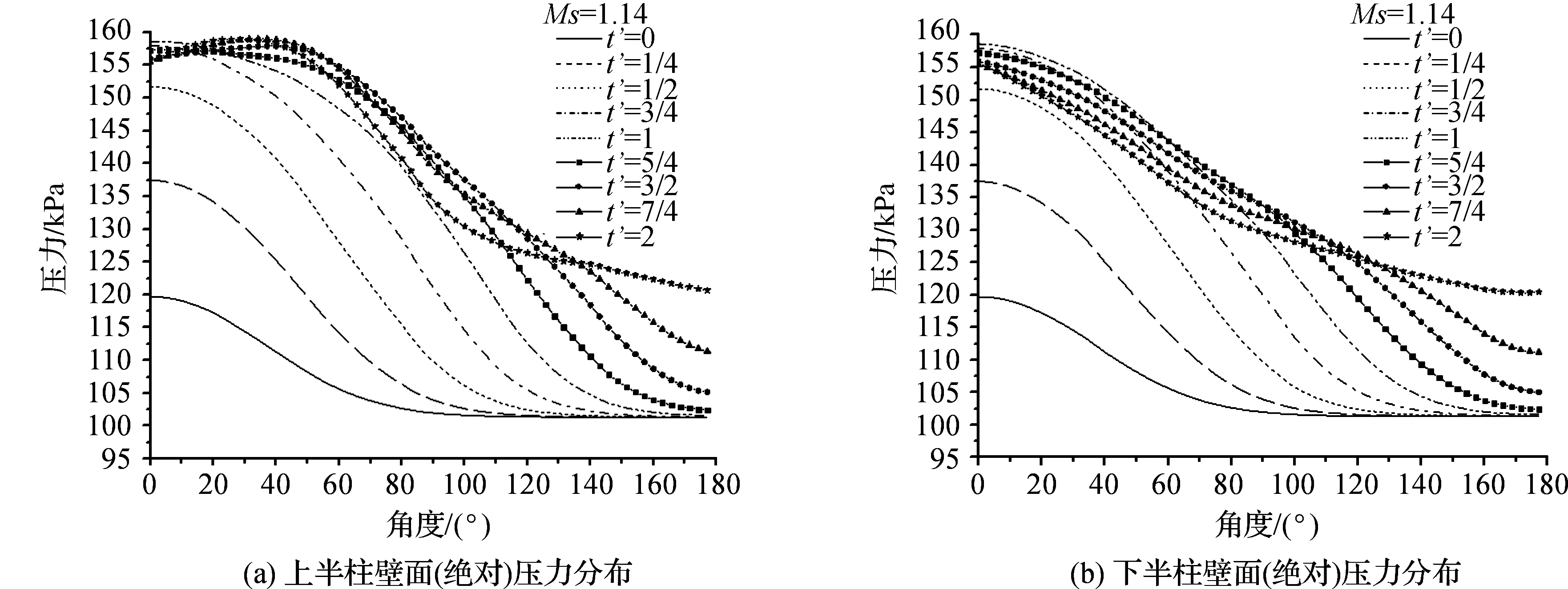
图9 不同时刻双柱壁面压力分布

双柱(H=1.5)第一波峰出现的原因与图3的单柱情形基本相同,针对单柱和双柱曳力系数曲线的差异,其根本原因是双柱沿激波传播垂直方向彼此之间空间位置的限制,使得隶属于每柱的激波结构可以发生相互干涉,从而影响了环绕每柱的压力以及柱壁面的压力和剪切应力分布。与单柱类似,对非稳态曳力而言,柱壁面的压力分布起关键作用,而壁面剪切应力只起次要影响。因此,从单、双柱壁面压力分布的差异和原因阐述造成上述3点曲线差异的具体原因。

首先,在t′=1/2时刻,双柱彼此空间位置限制使其间的激波阵面扭曲,引起双柱赤道左半区内侧壁面反射的激波发生相互干涉,导致t′=1/4～2期间赤道左半区内侧壁面分布的压力值相对于单柱的各对应时刻相同位置有所提升,同时由于激波被前驻点附近壁面反射而提升局部压力的叠加影响,这就使得t′=3/4时刻曳力(系数)在t′=1/4时刻基础上进一步提升,导致双柱曳力系数曲线第一波峰出现的时刻较晚,但峰值更大。

其次,双柱第二波峰的峰值更大,可解释为单柱的第二波峰是衍射波在后驻点的持续聚焦过后,后驻点近区压力降低造成的,视为一种被动形式的曳力升高;而双柱的第二波峰则是反射波经干涉后到达赤道左半区内壁面,造成该区域壁面压力提升,从而提高了曳力,视为一种主动形式的曳力提升。

最后,双柱曳力系数曲线波更难以趋于稳定的根本原因是源自双柱的反射波和衍射波的相互干涉以及到达对侧壁面后的再次反射和干涉,如此往复,使得绕柱流场压力、圆柱壁面压力和剪切应力波动变化更为复杂,这些参数分布趋于稳态需要经历更长时间,曳力系数达到稳态值也需要更长时间。

3 结 论

基于Fluent6.3计算平台对激波诱导单/双圆柱的绕流场和非稳态曳力进行数值计算,分析激波的反射、衍射和聚焦对非稳态曳力形成的机理。主要结论如下:

a) 在激波马赫数Ms=1.14条件下,单柱和双柱模型(H=1.5)的曳力系数Cd曲线的变化规律为出现明显的波峰和若干的负值波谷,并最终趋于稳定。

b) 在相同条件下,由于双柱相对空间位置在垂直于激波传播方向的彼此限制,导致反射激波、衍射波的相互干涉影响了圆柱壁面的压力和剪切应力的分布,从而出现双柱的第一波峰和第二波峰出现的时刻t′略晚,第一峰值和第二峰值都偏高以及双柱曳力系数曲线波动变化持续时间更长,更难以趋于稳态正值等曳力系数曲线间的差异。

c) 对于有运动激波存在的气固两相流,不能简单地采用单颗粒稳态曳力系数模型,当颗粒载荷比较大时,即无量纲间距较小时,需要考虑隶属于邻近的不同固体颗粒激波的波系结构的相互干涉对曳力的非稳态影响。

[1] Liu Y. Performance studies of particle acceleration for transdernal drug delivery[J]. Med Comput, 2006, 44: 551-559.

[2] Liu Y. Physical-Msther Mstical modeling of fluid and particle transportation for DNA vaccination[J]. International Journal of Engineering Science, 2006, 44: 1037-1049.

[3] 饶 琼, 周香林, 张济山, 等. 超音速喷涂技术及其应用[J]. 热加工工艺, 2004(10): 49-52.

[4] Saito T, Saba M, Sun M, et al. The effect of an unsteady drag force on the structure of a non-equilibrium region behind a shock wave in a gas-particle mixture[J]. Shock Waves, 2007, 17: 255-262.

[5] Dan I, Ozer I, Lazhar H, et al. Simulation of sphere’s motion induced by shock waves[J]. Journal of Fluids Engineering, 2012, 10(134): 1-4.

[6] Tanno H, Itoh K, Saito T, et al. Shock wave interaction with a sphere in a shock tube[C]//Symposium on Interdisciplinary Shock Wave Research, 2004: 483-497.

(责任编辑： 康 锋)

Numerical study of Unsteady Drag Force in Shock Wave’s Interaction with Single/Double Cylindrical Models

CHENWan-jun,ZHANGLi-te,SHIHong-hui,HAOLi-na,HUANGBao-qian

(School of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Two-dimensional numerical calculation of ambient flow field of single/double cylindrical models induced by the shock wave was conducted with Fluent software. Formation mechanism of unsteady drag force of ambient flow field was deeply studied during interactions between shock waves withMs=1.14 and single/double cylindrical models with the diameter of 40 mm. The results show that drag force coefficientCdof single/double cylindrical models (H=1.5) has significant wave crest and multiple troughs and gradually tends to a steady positive value in the form of decreasing amplitude. The wave peak value is much greater than the steady-state value. Compared with single cylinder, due to space position limit of dual cylinders, shock wave structure surrounding each cylinder may mutually interfere, which thus influences distribution of cylindrical pressure and shear stress and leads to differences of fluctuation changes of single/double cylindrical drag force coefficient curve.

shock wave; single/double cylinder; unsteady drag force; drag coefficient; interference

1673- 3851 (2015) 01- 0055- 07

2014-06-05

国家自然科学基金项目(51006091);浙江省自然科学基金项目(LY13E060011);流体机械及工程省重点学科及流体工程技术创新团队项目(11130031201301);流动腐蚀与防控技术创新团队(浙理工科〔2013〕13号)

陈婉君(1990-),女,浙江东阳人,硕士研究生,主要从事可压缩性气固两相流方面的研究。

章利特,E-mail:langzichsh@zstu.edu.cn

TK121

A