基于复小波变换的纺织品图案检索方法研究
罗戎蕾
(浙江理工大学, a. 服装学院; b. 浙江省服装工程技术研究中心, 杭州 310018)
基于复小波变换的纺织品图案检索方法研究
罗戎蕾a,b
(浙江理工大学, a. 服装学院; b. 浙江省服装工程技术研究中心, 杭州 310018)
针对海量数据中提取纺织品设计图案问题,引入面料视觉基础分类的横纹、竖纹、格纹等面料图像类概念,针对海量数据中提取纺织品设计图案问题,从而构建基于Dauchechies小波旋转变换和旋转复变换的多分辨率图像分解形成的特征表,代替传统方法下使用矩阵的均值和方差作为特征纹理数据的方法,除了尺度和位移两个参量外,增加了一个方向参量,具有更好的方向辨识能力,从而对图像的边缘,如曲线、直线等几何特征的表达有一定优势。研究结果可以为基于内容的面料图案图像数据库检索提供基础理论依据。
小波变换; 复小波; 旋转小波图像检索; 面料图案
0 引 言
作为服装设计、面料设计灵感和表现的主要形式,图案在艺术设计行业内已经得到广泛和深入的应用,然而设计者们和顾客根据所谓的风格和感觉从海量数据中查询到所需的风格图案是异常繁琐的问题。而纹理作为重要的低层视觉特征受到了广泛的关注,目前纹理特征提取是基于内容图像检索算法的一个的主要方向。相对于传统的纹理特征提取方法,基于小波变换的算法在颜色分布特征提取方法具有更好的频率定位而受到国内外学者的长期关注,也是目前研究的热点[1-7]。早期,Manjunath[8]以及Tian等[9]提出基于Gabor变换的纹理特征分析方法可以提取到和视觉感知有意义的图像属性和规律;Balmelli等[10]尝试使用小波域的图像特征实现对内容的图像检索;随后,根据小波变换的多分辨率理论,研究人员提出旋转和尺度不变的纹理特征分析方法,但纹理方向信息有一定程度的损失[11-12];对于改进Garbor滤波器的研究表明,其旋转、尺度不变纹理特征计算具有较高的复杂度[13];Pun[14]基于Log-polar的方法是用平移变化代替尺度变量来进行计算,但频率信号特征收到损伤。对于二维图像处理,常用的二维小波变换的基函数是各向同性的,Gluekman[15]认为纹理的描述只是利用子波变换后的均值与方差是不够充分的,变换系数的局部模极大值只能反映出这个小波系数出现的位置,而无法表达方向与边缘的信息。针对小波变换的上述缺点,Candes等[16]提出第一代Curvelet变换理论,与小波变换不同,除了尺度和位移两个参量外,增加了一个方向参量,具有更好的方向辨识能力,从而对图像的边缘,如曲线、直线等几何特征的表达有一定优势。另外,Kokare等[17]、Miller等[18]、Huang等[19]利用复小波的旋转不变性和较强的方向选择性,提出基于复小波的图像检索算法具有较好的纹理检索效果,但同样使用的一阶统计特征量。同时,关于复小波变换与其它纹理检索方法的结合,例如Clausi等[20]设计与其它统计方法相融合的纹理特征提取方法,以改进纹理识别,产生较高的特征空间分离,分类正确率较单独的特征集有一定提高。
值得注意的一点是,对于设计类图案的检索与其他工程类图像检索(例如医学图像检索)有一个显著的差异,设计类图像检索的目标在于检索视觉感官和风格的相似性,不要求精确的图像检索识别。此外,对于面料图案还有一些独特的图案特性,比如图案循环、设计图案中存在基础图案及基础图案的变形等特性。而事实上,根据不同特性的图像应该提取不同的纹理特征才能达到较好的效果。根据文献跟踪和前期研究基础,我们注意到,基于面料图案特性的图像检索技术的研究较少,面料纹理图案特性及其分类与图像检索技术之间的联系尚未被充分研究。
因此,本文引入面料视觉基础分类的横纹、竖纹、格纹等面料图像类概念,以行列信息相关的特征序列作为特征表的类特征分类,从而构建基于Dauchechies小波旋转变换和旋转复变换的多分辨率图像分解形成的特征表,是进行面料图像分类的基础信息,弥补传统小波变换后的图案方向性信息缺失的问题。与用颜色值进行图像面料检索,本研究针对图像结构特性和方向特性进行分类检索。
1 基于旋转小波变换面料图像的纹理特征
对图像进行2D的一层小波分解,可以表示为(图1):
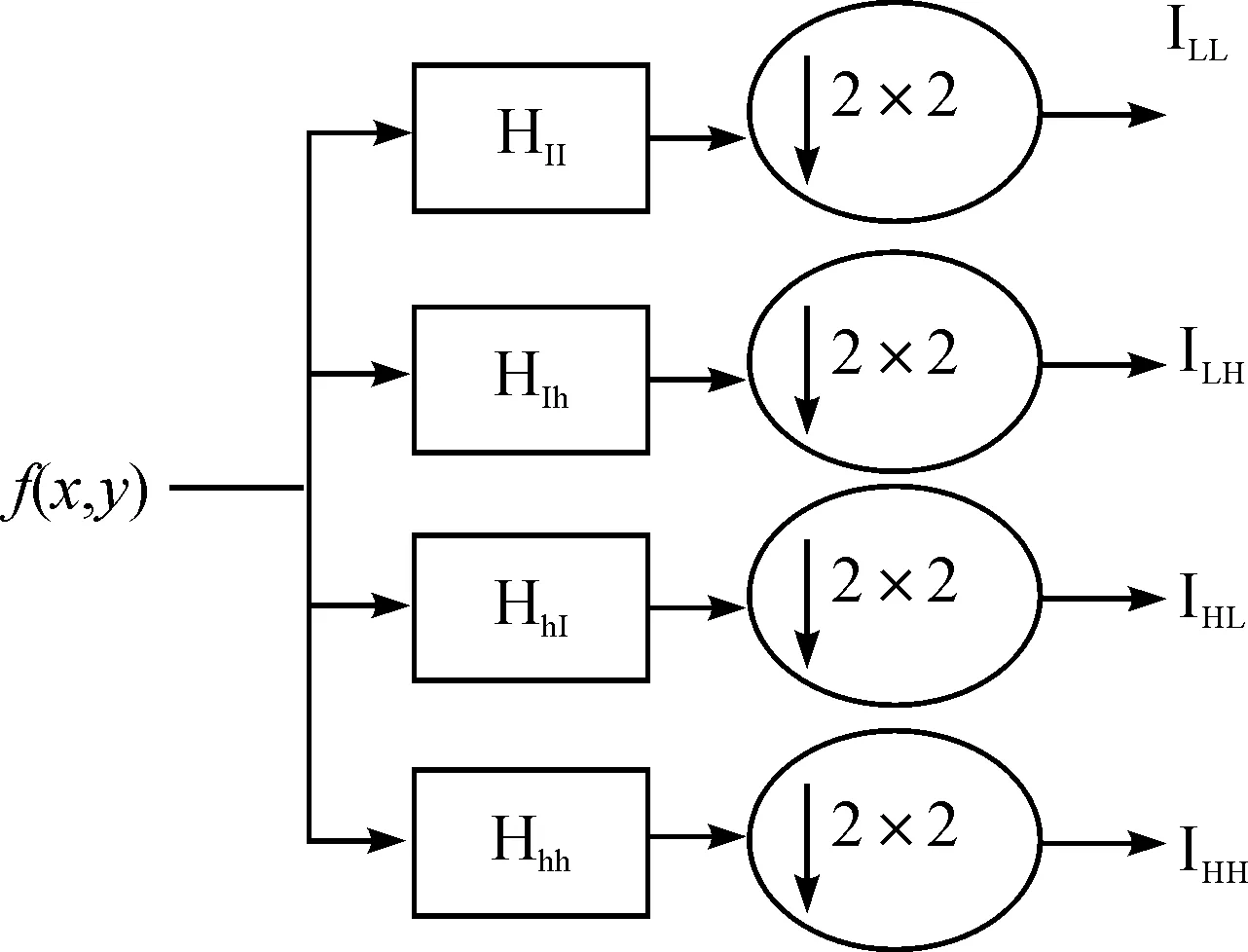
图1 离散小波变换的一层分解
二维小波变化在经过一层小波分解后,函数的频域的分区情况如图2所示。
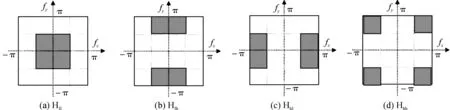
图2 二维离散小波变换后的函数频域分区
由图2可知,对于标准的离散小波变换,分量IHH,保留的是图像对角线的一些信息,但是并不能确定是450,还是1 350方向的信息,而对于面料纹理和图案的检索来说,方向是至关重要的。因此,课题组选择重新设计一种不可分离的具有方向性的小波变换(从不旋转到无法提取再到方向数据),方法是将传统的2D离散小波滤波进行45°旋转,从而分解的方向发生了改变,如图3所示。
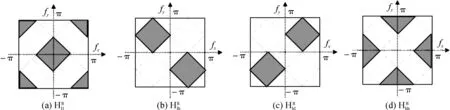
图3 旋转小波变换后的图像频域分区
由图3可知,2D的高通、低通的滤波系数可以得到:HLL=hTH,HLH=hTg,HHL=gTh,HHH=gTg,其中,h,g分别表示Daubechies高通和低通系数。旋转后的小波变换的计算量与传统的小波变换是一样的。首先,对面料图像进行尺度变化,对原始面料图案图像和变化后的面料图案图像分别进行二维旋转小波变换2D-RWT;在输出系数取绝对值后,转化为实数,并分别计算各个子带的能量,将2组计算数据在尺度的维度上进行插值计算,构成一个特征矩阵表。可以发现,该特征矩阵的列方向为尺度维,行方向为旋转维,从而进行尺度及旋转不变的特征向量的提取。
对于复小波变换(如图4所示),上部分的树结构滤波器组表示复小波变换的实部,下部分树结构滤波器组表示复数小波变换的虚部,数值2则表示其为隔点取样。面料图案图像在经过复变换之后,其系数具有近似平移不变性、方向各异性和系数对应性等特点。笔者对面料图案图像进行二层小波复变换,从而获得每幅面料图案图像的复数小波子带的特征系数。本文使用的双数小波变换是使用二个独立的离散小波变换平行作用来完成复数小波变换,而输入数据相同,变换后所产生的两组分解系数分别作为复数输出结果。二维双树复小波变换2D-DWT对图像检索中的查询图像和目标图像进行分解,为了提取到输入图像的6个方向上的特征信息,实现旋转不变性分析,根据算法提取6个小波子带的主方向,分别为{+150,+450,+750,-150,-450,-750}。在对查询图进行双树复小波变换后,利用行列序列C(d)来替换传统方法下使用一阶统计特征值,并将数据归一化,作为特征纹理数据的方法,形成特征检索结构。
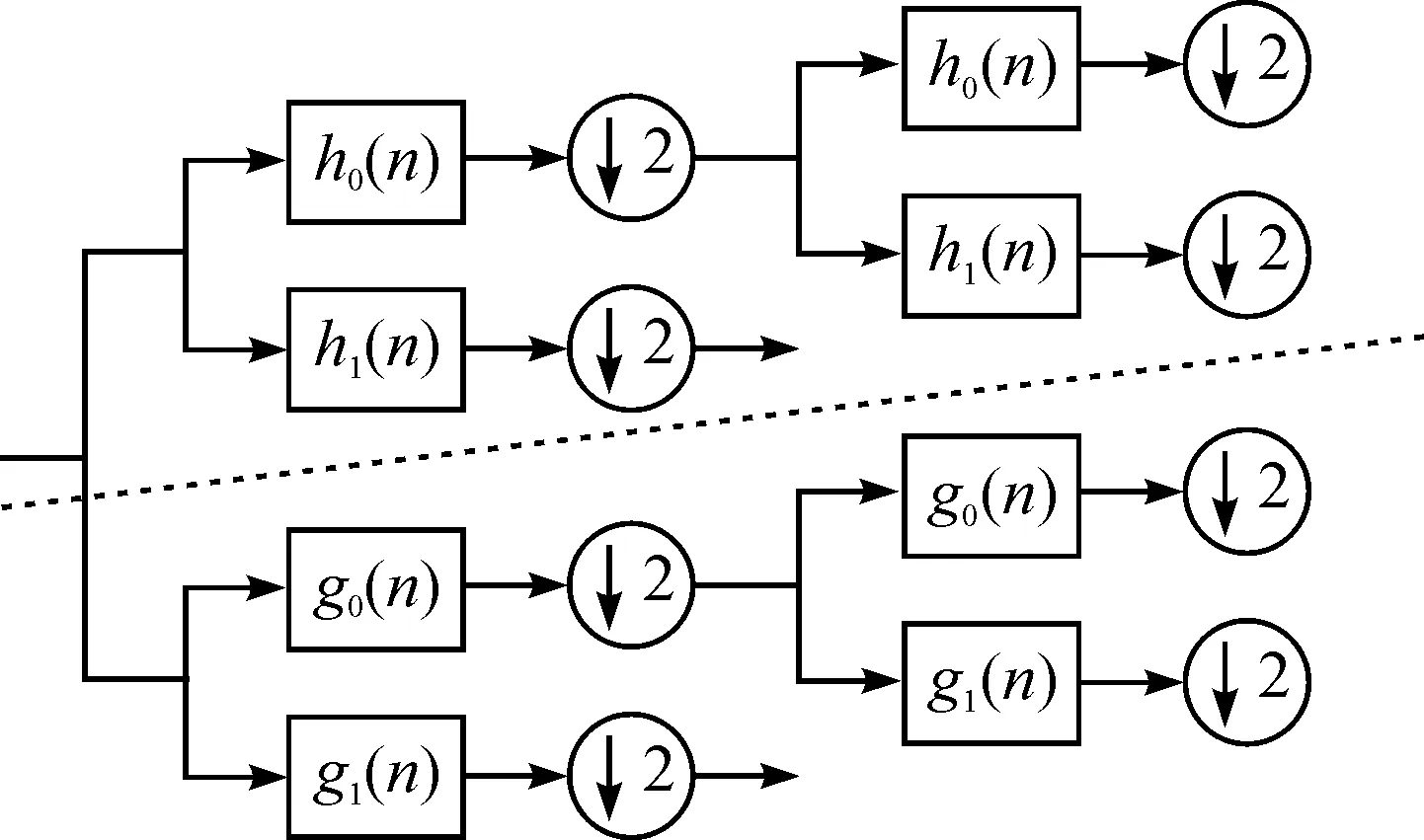
图4 双树复小波图像分解
2 面料横纹、竖纹、格纹等面料基础纹理的特征选取
基于以上分析,笔者对面料图像进行视觉纹样分类,面料分类有很多种,在这里首先研究面料基础图案中的横纹、竖纹、格纹、花版。为面料图像各个分类下做二维双数复小波变化(2D-DWT),在这里首先使用Daubechies小波分解。利用DT-CWT对每幅256×256像素的图像块进行4尺度小波分解,然后对变换后每一尺度的高频带子图分别计算6个方向小波系数模的均值μij和标准方差σij,i,=1,2,3,4,j=1,2,3,4,5,6,将系数取绝对值后,转化为实数,提取各个子带的方差,然后将2组数据在尺度维上进行插值计算,构建完成包含行列信息的特征序列C(d):
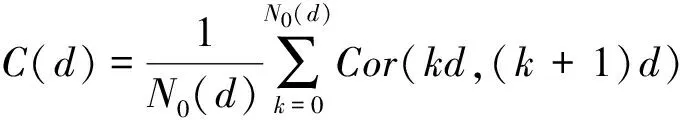
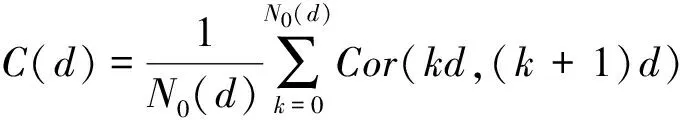
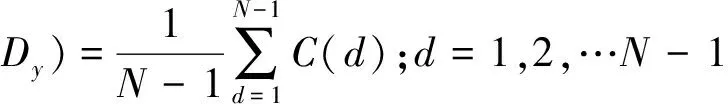
对不同类型的面料图像的特征数列Dx,Dy(是方向特征值上面有公式说明)进行分析,发现类型不同,其数值分布在不同的特征区域,从而可以表征其特征形态,作为分类检索的依据。
3 结果和分析
从服装流行资讯公司面料库提取相关4类面料图案500张,包括横纹、竖纹、格纹、花卉图案,规格化为256×256 dpi。图5是部分典型面料图案。

图5 典型面料图案示例
对面料图案进行分解计算,得到各种面料的Dx,Dy,部分结果如表1所示。从表中可以发现,横纹或者竖纹图案,其Dx(或Dy)具有明显差异,并与横纹竖纹方向成正相关性;格子图案其Dx和Dy的值量大,而花卉图案其Dx和Dy的方向值量都较小。对500幅图案计算所得结果归纳可以得到Dx和Dy主要分布范围,为基础面料分类的图像纹理特征表,如表2所示。
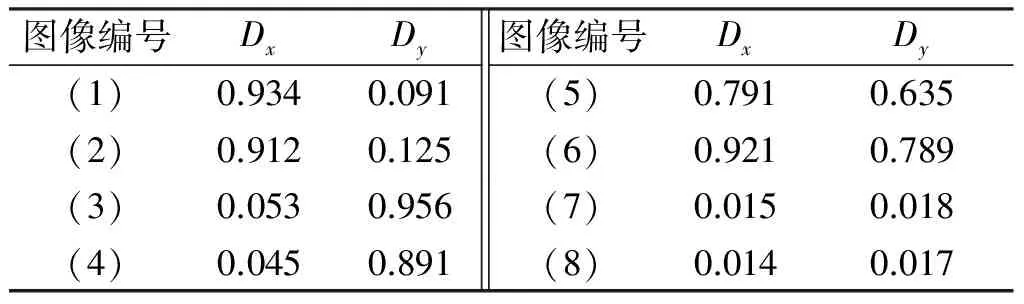
表1 部分面料图案的方向特征值
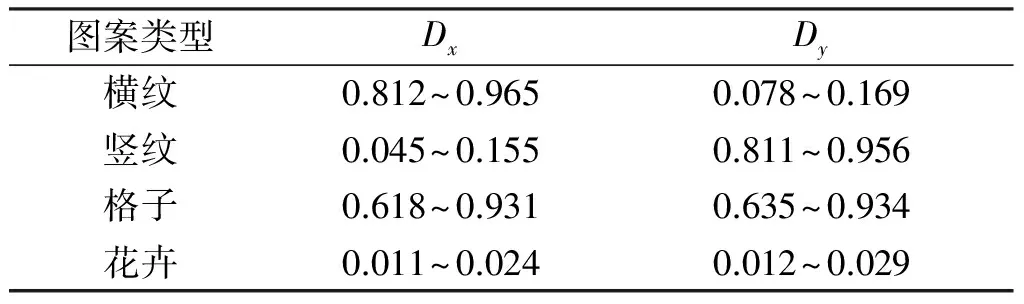
表2 各类图案面料的方向特征值范围
4 结 论
本文提出建立包含图像小波分解系数的行列特性的相关序列,根据双数小波进行旋转小波变换和复小波变换得到的变换结果,构建以小波系数为信息基础,包含子带行列信息的特征序列形成面料不同类纹理的特征表,来代替传统方法下使用一阶统计特征数据为特征纹理数据的方法,从而形成图像纹理特征表。引入旋转小波变换和旋转复小波变换得到的C(d)序列构成面料类纹理的特征表,弥补传统小波变换后的图案方向性信息缺失的问题。进一步方向可以细化每种图案类型的花形尺寸检索及拓展到其他类型面料图案特征纹理数据研究。
[1] Celik T, Tjahjadi T. Texture classification and retrieval based on complex wavelet subbands[C]// Computer and Information Sciences: Proceedings of the 25th International Symposium on Computer and Information Sciences, 2010: 259-264.
[2] Kwitt R. Lightweight probabilistic texture retrieval[J]. IEEE Transactions on Image Processing, 2010, 19(1): 241-253.
[3] Zhu X, Shao Z. Using no-parameter statistic features for texture image retrieval[J]. Sensor Review, 2011, 31(2): 144-153.
[4] Priya K J, Rajesh R S. Local statistical features of dual tree complex wavelet transform on parallelogram image structure for face recognition with single sample[C]//International Conference on Recent Trends in Information, Telecommunication and Computing, 2010: 50-54.
[5] Xavier L, Bella M, Thusnavis B, et al. Content based image retrieval using textural features based on pyramid-structure wavelet transform[C]//3rd International Conference on Electronics Computer Technology, 2011: 79-83.
[6] Gonde A, Maheshwari R, Balasubramanian R. Rotated complex wavelet transform with vocabulary tree for content based image retrieval[C]// Proceedings of the 1st International Conference on Intelligent Interactive Technologies and Multimedia, 2011: 284-291.
[7] Quellec G, Lamard M, Cazuguel G. Adaptive non-separable wavelet transform via lifting and its application to content-based Image retrieval[J]. IEEE Transactions on Image Processing, 2010, 19(1): 25-35.
[8] Manjunath B, Ma W. Texture features for browsing and retrieval of large image data[J]. Pattern Analysis and Machine Intelligence, IEEE Transactions, 1996, 18(8): 837-842.
[9] Tian Q, Sebe N, Lew M S, et al. Image retrieval using wavelet-based salient points[J]. J. Electron. Imaging, 2001, 10(4): 835-849.
[10] Balmelli L, Mojsilovic A. Wavelet domain features for texture description classification and replicability analysis[C]// IEEE Interuational Conference Image Process, 1999: 440-444.
[11] Manthalkar R, Biswas P, Chatterji B. Rotation and ccale invariant texture features using discrete wavelet packet transform[J]. Pattern Recognition Letters, 2003, 24(14): 2455-2462.
[12] Jafari K, Khouzani H, Soltanian Z. Rotation-invariant multiresolution texture analysis using radon and wavelet transform[J]. IEEE Trans on Image Processing, 2005, 14(6): 783-795.
[13] Ju H, Ma K. Rotation-invariant and scale-invariant gabor features for texture image retrieva1[J]. Vision and Image Computing, 2006, 25(9): 1474-1481.
[14] Pun C M, Lee M C. Log-polar wavelet energy signatures for rotation and scale invariant texture classification[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2003, 25(5): 590-603.
[15] Gluekman J. Visually distinct patterns with matching subband statistics[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2005, 27(2): 252-264.
[16] Candes E, Demanet L, Donoho D. Fast Discrete Curvelet Transforms[R]. Pasadena: California Institute of Technology. Applied and Computational Mathematics. 2005: 1-43.
[17] Kokare M, Biswas P, Chatterji B. Texture image retrieval using new rotated complex wavelet filters[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part B: Cybernetics, 2005, 35(6): 1168-1178.
[18] Miller M, Kingsbury N. Image modeling using interscale phase properties of complex wavelet coefficients[J]. IEEE Transactions on Image Processing, 2008, 17(9): 1491-1499.
[19] Huang R, Lang F, Dong S. Color image retrieval based on moments and DT-CWT[C]// International Conference on Multimedia Technology, 2011: 2998-3001.
[20] Clausi D, Deng H. Design-based texture feature fusion using garbor filters and co-occurrence probabilities[J]. IEEE Transactionson Image Processing, 2005, 14(7): 925-936.
(责任编辑: 杨一舟)
Study on Textile Pattern Retrieval Method Based on Complex Wavelet Transformation
LUORong-lei
(a. School of Fashion Design and Engineering; b.Zhejiang Provincial Research Center of Clothing Engineering Technology, Zhejiang Sci-Tech University, Hangzhou 310018, China)
In allusion to extracting textile design patterns from mass data, this paper introduces transverse stripes, vertical stripes and cross stripes as the standard of classification and constructs feature list which forms through multiresolution picture breakdown based on Dauchechies wavelet rotation transformation and rotated complex transformation. This replaces traditional method which uses mean value of matrix and variance as characteristic texture data. Apart from scale and displacement, direction parameter is added. Thus, it owns better direction identification ability and has certain advantages for expressing image edge and geometrical characteristics such as curve and straight line. The research results can provide basic theoretical basis for content-based fabric image database retrieval and own certain theoretical reference value and practical application significance.
wavelet transformation; complex wavelet; rotated wavelet image retrieval; fabric pattern
1673- 3851 (2015) 01- 0046- 05
2014-01-06
浙江自然科学基金项目(LQ12F02018);浙江省重点科技创新团队计划资助(2011R50004);纺织科学与工程一级学科中青年拔尖人才培养计划(11110532241405)
罗戎蕾(1974-),女,浙江杭州人,副教授,博士,主要从事服装计算机辅助设计方面的研究。
TS941.26
A

