基于滑模趋近律的潜空导弹垂直出水姿态控制律设计*
苗昊春,马清华,陈 韵,严宪军,张爱戈
(1 西北工业大学航天学院,西安 710072;2 中国兵器工业第203研究所,西安 710065)
基于滑模趋近律的潜空导弹垂直出水姿态控制律设计*
苗昊春1,马清华2,陈 韵2,严宪军2,张爱戈2
(1 西北工业大学航天学院,西安 710072;2 中国兵器工业第203研究所,西安 710065)
文中给出了一种滑模趋近律应用于潜空导弹垂直出水姿态控制的设计方法。首先利用四元数在弹体坐标系下对垂直出水的潜空导弹水下和空中运动建立了统一的运动方程形式,然后在纵向通道利用小扰动线性化状态空间模型,设计了基于滑模趋近律的姿态控制律,最后建立了Simulink六自由度弹道模型并进行了数字仿真。结果表明:基于四元数的水下、水上统一的运动方程形式运行有效,基于滑模趋近律的姿态控制律可实现对潜空导弹垂直出水的有效控制。
潜空导弹;垂直出水;四元数;滑模;姿态控制
0 引言
潜空导弹对潜艇提升攻击、威慑反潜机的主动防御能力具有重大军事意义。国外现已研究或装备的潜空导弹有英国“斯拉姆”、美国“西埃姆”、法国“米卡”以及德国“IDAS”等。
在潜空导弹的建模、制导控制设计和出水前后的弹体特性对比等方面研究资料较少,现有研究往往以水雷为主兼顾出水,文献[1]对潜射导弹水下及出水运动进行建模并采用模糊PID控制方法进行了仿真分析,文献[2]等对潜空导弹运载器建立了水下六自由度模型并进行了水弹道研究。
潜空导弹垂直出水可以360°全范围攻击空中目标,并可为目标探测装置提供良好的工作条件,具有很高的战术应用价值,文献[3-4]对鱼雷出水攻击空中弹道进行了研究,文献[5-6]对鱼雷出水过程建立了仿射非线性模型并设计提出滑模反演控制方法,目前尚未有滑模控制方法应用于潜空导弹出水姿态控制的相关研究。
文中分别以鱼雷航行力学[7]和导弹飞行力学[8]为基础,提出了基于滑模趋近律的潜空导弹垂直出水姿态控制设计方法,首先利用四元数对导弹水下和空中运动给出了统一的运动方程形式,并在纵向通道分别建立小扰动线性化的状态空间模型,然后设计了基于指数趋近律的滑模姿态控制律,最后给出了Simulink六自由度弹道仿真计算结果,实现了潜空导弹垂直出水的水下和空中弹道。
1 潜空导弹运动方程
潜空导弹的的动力学和运动学方程分为水下和空中两部分,在水下时导弹相当于鱼雷,其运动规律符合鱼雷航行力学,在空中,其运动规律符合导弹飞行力学。
文中研究的潜空导弹以德国“交互式潜射防空武器系统(IDAS)”为蓝本,轴对称外形,正常式“X-X”气动布局,下面建立其动力学和运动学方程。

图1 德国IDAS外形示意图
1.1 潜空导弹动力学方程
在以浮心为原点的雷体坐标系中建立的鱼雷动力学方程和以质心为原点的弹体坐标系(定义同雷体坐标系)中建立的导弹飞行力学方程可以统一表示如下:
(1)
对于鱼雷有:
(2)
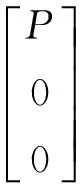
(3)
(4)

对于导弹有:
(5)
Fx、Fy、Fz和Mx、My、Mz在弹体坐标系下的表达式与方程组(3)、(4)相同,但不同的是ΔG表示重力,Ri、MRi(i=x,y,z)分别表示气动力、气动力矩,其具体计算见文献[8]。
1.2 潜空导弹运动学方程
鱼雷的浮心和导弹的质心在地面坐标系下的运动学关系式可以统一表示如下:
(6)
(7)
其中x、y、z表示浮心或质心在地面系下的位置,ϑ、ψ、γ分别表示俯仰、偏航、滚转角,地面系到弹体坐标系的转换矩阵为:
(8)
1.3 几何关系式
攻角、侧滑角计算如下:
(9)
文中研究的潜空导弹特点是垂直出水,欧拉角描述的运动方程系数矩阵、坐标转换矩阵在俯仰角为90°时是奇异的,因此采用四元数来表示导弹的方位。
四元数与姿态角具有如下转换关系:
(10)
(11)
由以上转换关系可以将姿态角初值转换为四元数数值积分初值,或者将当前解算的四元数计算姿态角用于控制指令生成。
用四元数表示鱼雷绕浮心或导弹绕质心运动方程,则方程组(7)变为:
(12)
由于积分误差的存在破坏了四元数变换的正交性,因此需要对范数进行修正:
(13)
用四元数表示地面坐标系到弹体坐标系转换矩阵:
(14)
因此,方程组(1)、(2)、(9)、(12)、(13)即组成了四元数表示的潜空导弹动力学和运动学方程,式(10)用于赋四元数积分初值,式(11)用于解算姿态角。
2 潜空导弹运动方程线性化
潜空导弹运动方程显然为非线性时变系统,直接用于设计控制系统是非常困难的。为了进行潜空导弹控制系统设计,控制潜空导弹实现期望弹道,需要对潜空导弹动力学和运动学方程进行简化。假定导弹在受到小扰动时,扰动运动参数与同一时间内的未扰动运动参数相差很小(即小扰动假设),则运动方程可以进行线性化处理,在此针对鱼雷和导弹直接给出线性化结果。
2.1 鱼雷纵向运动状态方程


(15)
其中:
式中的系数aij为鱼雷纵向扰动运动方程式系数,计算公式见文献[7]。
2.2 导弹纵向运动状态方程


(16)
其中:
式中的aij为导弹纵向扰动运动方程式系数,计算公式见文献[8]。
3 基于滑模趋近律的姿态控制律设计
文中主要研究潜空导弹的水下爬升和空中爬升两段弹道,在此给出统一的滑模变结构设计方法。
对连续时间线性系统:

(17)
设姿态指令信号为r,则误差为:
e=r-ϑ
(18)
误差变化率为:
(19)
设误差向量E和系数向量C为:
(20)
则可以选取切换函数s为:
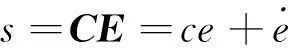
(21)
对该函数求导,有:
(22)
采用指数趋近律作为滑模趋近律:

(23)
其中,k是指数趋近项的系数,反映运动点从远到近趋近滑模面的速度成相应指数规律,在趋近过程中,趋近速度从一较大值逐步减小到零,不仅缩短了运动时间,而且使运动点到达切换面时速度很小。ε是等速趋近项的系数,反映运动点趋近滑模面的恒定运动速度,到达切换面时增加等速趋近项,使趋近速度不为零[10]。二者相结合可保证运动点在有限时间内到达滑模面。
由李亚普诺夫稳定性理论易知,式(23)的滑模到达条件成立。
将式(23)代入式(22),可计算得到控制律:
εsgn(s)+ks]/B2
(24)
该控制律可用于水下和出水后的姿态控制,对于垂直出水,水下姿态指令为:
r=π/2
(25)
出水后的姿态指令信号为一组设计的姿态曲线ϑ*,计算公式如下:

(26)
其中:t1为垂直控制结束并开始转弯时刻;t2为转弯结束时刻。
4 数字仿真
文中研究的潜空导弹具有巡航和增速两级动力,并具有燃气舵作为推力矢量控制机构,导弹从鱼雷管中弹射后巡航发动机点火,导弹开始水下航行,深度为10 m,5 s后以转水下姿态控制,俯仰角为90°,出水时刻增速发动机点火,燃气舵工作,导弹垂直上升2.5 s后按程序姿态角转弯。
姿态控制参数c反映对误差的容忍程度,一般取1~20,参数k反映滑模指数趋近速度,一般取1~30,参数ε=0.1反映等速趋近速度,一般取0.01~1。经计算,潜空导弹在水下和空中两种介质中的弹体纵向特性差别巨大,如表1所示,水下阻尼系数和时间常数远大于空中,因此在设计姿态控制参数时,选用较大的滑模指数趋近参数k和较小的等速趋近参数ε=0.1,以获得较快、较精确的控制效果。
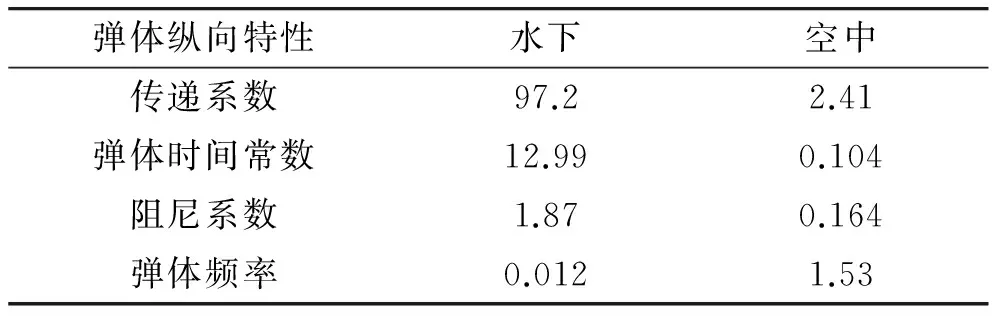
表1 弹体特性参数
水下姿态控制参数:
c=5,ε=0.1,k=10
空中姿态控制参数:
c=8,ε=0.2,k=8
依据鱼雷航行力学和导弹飞行力学方程,对潜空导弹建立Matlab/Simulink六自由度弹道仿真模型,数字仿真结果如图2~图5所示。

图2 高度曲线

图3 俯仰角曲线

图4 速度曲线

图5 攻角曲线
仿真结果可见,导弹在水下10 m航行5 s后转姿态控制,6.9 s垂直出水,出水时刻俯仰角为89.7°,最大攻角为14°,出水后增速发动机使速度从7 m/s迅速增加到154 m/s,9.4 s导弹结束垂直飞行开始转弯,此时高度约300 m,15.9 s程序转弯结束,转弯过程中最大攻角约为-26°,最大高度720 m,转弯结束后导弹飞行稳定,具备转入下一阶段巡航或攻击的飞行条件。
5 结论
文中以德国“IDAS”为背景,利用四元数在弹体坐标系下对潜空导弹的水下和空中运动建立了统一的运动方程形式,并在纵向通道分别建立小扰动线性化的状态空间模型,设计了基于指数趋近律的滑模姿态控制律,最后进行了Matlab/Simulink六自由度弹道仿真。仿真结果表明:基于四元数的水下、水上统一的运动方程简单有效,基于滑模趋近律的姿态控制律可实现对潜空导弹水下姿态和空中姿态的有效控制。文中的工作对潜空导弹的跨介质制导控制系统研究提供了一个参考。
[1] 崔乃刚, 曹春泉, 韦常柱. 潜射导弹水下运动过程仿真分析 [J]. 弹道学报, 2009, 21(2): 95-99.
[2] 张海军, 罗震. 潜空导弹运载器控制系统设计与仿真 [J]. 系统仿真学报, 2009, 21(23): 7585-7588.
[3] 李雨田, 张宇文, 张纪华, 等. 水雷出水攻击空中弹道设计与分析 [J]. 鱼雷技术, 2012, 20(3): 166-170.
[4] 张纪华, 张宇文, 范辉. 水雷攻击直升机弹道设计与仿真 [J]. 鱼雷技术, 2011, 19(3): 172-175.
[5] 肖敏, 史忠科. 水雷出水突变非线性滑模自适应反演弹道控制 [J]. 信息与控制, 2012, 41(6): 33-40.
[6] 肖敏, 史忠科. 水雷出水模型突变的控制方法 [J]. 自动化学报, 2012, 38(10): 1609-1617.
[7] 严卫生. 鱼雷航行力学 [M]. 西安: 西北工业大学出版社, 2003.
[8] 钱杏芳, 林瑞雄, 赵亚男. 导弹飞行力学 [M]. 北京: 北京理工大学出版社, 2000.
[9] 张宇文. 鱼雷弹道与弹道设计 [M]. 西安: 西北工业大学出版社, 1999.
Attitude Control Law Design of Vertical Water-exit of Submarine-to-air Missile Based on Sliding Mode Control
MIAO Haochun1,MA Qinghua2,CHEN Yun2,YAN Xianjun2,ZHANG Aige2
(1 School of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China; 2 No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
A design method of sliding mode approaching law was applied in attitude control of vertical water-exit of submarine-to-air missile. Firstly, quaternion was used for submarine-to-air missile of vertical water-exit to establish a unified equation form of underwater and in air motion in missile’s body coordinate system, then the small perturbation linearization state space model was adopted in pitch channel to design attitude control law based on sliding mode approaching law, finally the 6-DOF trajectory simulation model in Simulink was established and simulated. The result indicates that the unified equation form of underwater and in air motion using quaternion is efficient, and attitude control law based on sliding mode approaching law is practicable in vertical water-exit control of submarine-to air missile.
submarine-to-air missile; vertical water-exit; quaternion; sliding mode; attitude control
2014-04-15
苗昊春(1986-),男,内蒙古赤峰人,工程师,博士研究生,研究方向:导弹制导与控制。
V249.1
A

