基于弹着点椭圆散布的射击方位角选取*

王立安,徐卫昌,李永峰,刘继方,张高瑜

(1 第二炮兵工程大学士官职业技术教育学院, 山东青州 262500;2 96451部队, 吉林白山 135200)

基于弹着点椭圆散布的射击方位角选取*

王立安1,徐卫昌1,李永峰1,刘继方1,张高瑜2

(1 第二炮兵工程大学士官职业技术教育学院, 山东青州 262500;2 96451部队, 吉林白山 135200)

根据弹道导弹落点椭圆散布规律,构建射击方位角选取模型。针对矩形目标,可直接通过公式遍历筛选;而针对一般面目标,提出用粒子群算法搜索最佳射击方位角。实例计算结果表明,大长宽比目标轴向射击命中概率最大;而针对小长宽比目标和一般面目标,可通过公式遍历筛选和粒子群搜索算法选取最佳射击方位角。

椭圆散布;射击方位角;公式遍历筛选;粒子群搜索算法

0 引言

导弹在实际的飞行中,由于纵向、横向的飞行控制不同,弹着点纵横向散布方差一般也不相同。对弹道导弹而言,它的落点规律接近椭圆散布,因此,在不同的方位对目标进行打击时,命中概率必然有差异。文献[1]研究了射向变化对机场跑道失效率的影响,但没有给出最佳射向的选取办法;文献[2]仅讨论了轴向和垂向射击矩形目标时,长宽比与命中概率之间关系。文中基于导弹实际落点的椭圆散布规律,通过构建模型,探讨射击方位角改变对导弹命中概率的影响,提出采用针对矩形目标的公式遍历筛选法乃至针对一般面目标的粒子群搜索算法选取最佳射击方位角,为导弹阵地部署和火力打击方案拟制提供参考

1 矩形目标射击方位角的选取

在实际战争中,矩形或类似矩形目标非常常见,如机场跑道、公路桥梁、铁路桥梁、跨海大桥、舰船等,对它们的精确打击必然成为部队决胜未来战场的重要因素,很有必要有针对性的选择合适的射击方位角打击此类目标。

1.1 假设条件

1)弹着点散布规律及毁伤半径与射击方位角无关,矩形目标内各点的毁伤律一样;

2)矩形目标的长宽分别为a、b(a≥b),导弹纵向、横向落点分布标准差分别为δy、δz,相关系数为r,系统误差为(y0,z0);

3)导弹瞄准点为矩形目标的中心,落点散布概率密度函数是以散布点中心为中心的二维正态分布,则其概率密度函数为[3]:

(1)

4)基于矩形目标的中心对称性,为方便计算,约定导弹射击方位角α为射击方向与目标长轴方向所夹的较小的角,即0≤α≤π/2,如图1所示。

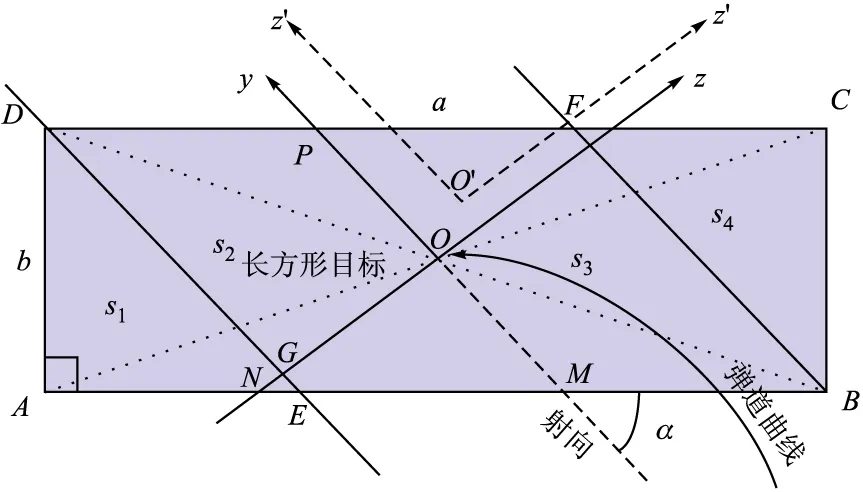
图1 矩形目标射击方位角

1.2 模型建立

根据假设条件2)、3),在弹着点散布规律和矩形目标参数已知的条件下,导弹命中概率仅与射击方位角有关,射击方位角选择越合理,导弹的命中概率就越大。文中建立针对矩形目标的公式遍历筛选方法,具体如下:

首先,以导弹的瞄准点O为中心,以射击方向为y轴,以位于目标平面内且垂直于y轴的直线为z轴构建直角坐标系,y轴与AB边所夹的角即为射击方位角α,如图(1)所示。导弹的命中概率p即为落点偏差概率分布密度函数在目标区域内的积分,即:

p=∬sf(y,z)ds

(2)

式中s表示矩形目标区域。

为方便计算,分别过D、B点做平行于y轴的直线DE、BF,将矩形目标分为三角形ADE、四边形DEMP、四边形MPFB、三角形BCF四块,分别记为s1、s2、s3、s4,如图(1)所示,所以:

p=∬s1f(y,z)ds+∬s2f(y,z)ds+∬s3f(y,z)ds+

∬s4f(y,z)ds

(3)

因为三角形ADE和三角形BCF、四边形DEMP和四边形MPFB关于O点对称,所以:

p=2∬s1f(y,z)ds+2∬s2f(y,z)ds

(4)

1.3 模型求解

对式(4)的计算包括目标区域点位确定及在目标区域内积分。

1)目标区域点位确定

在yoz平面内,只要计算出A、D、E点坐标,即可进行概率积分计算。首先延长y轴交AB于M点,然后延长z轴分别交DE、AB于G、N点,如图(1)所示。

根据已知条件,|AB|=b,∠OMN=α,所以|AE|=b·cotα,|DE|=b/sinα。

2)在目标区域内积分

根据式(4),导弹的命中概率为:

(5)

对式(5)进行数值近似求解就可以遍历计算不同射击方位角下的命中概率,以便筛选出命中概率最大时的射击角度。

2 一般面目标射击方位角选取

公式法实现了对矩形目标射击方位角的遍历筛选,但如何选取针对非矩形目标最佳射击方位角呢？文中利用现代优化算法的特点,采用粒子群算法搜索非矩形面目标的最佳射击方位角。

2.1 粒子群算法简介

粒子群优化算法(particle swarm optimization,PSO)是由Kennedy和Eberhart在研究鸟类和鱼类的群体行为基础上于1995年提出的一种群智能算法[4]。算法首先初始化一群随机粒子,然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个“极值”即个体极值和全局极值来更新自己的速度与位置。根据文献[5],更新速度、惯性权重、位置公式如下:

式中:i为迭代次数;imax为最大迭代次数;w为惯性权重;wmax、wmin分别为最大最小惯性权重系数,一般设为0.9、0.5;pid、pgd分别为局部和全局最优位置;xid为第i个粒子在第d维的位置;vid、v(i+1)d分别为第i、i+1步的更新速度;rand()为0到1之间的随机数;c1、c2为加速系数,通常取2。

2.2 假设条件

导弹射击方位角α为射击方向与正北方向所夹的角,如图2所示。

图2 一般面目标射击方位角

2.3 算法与求解

1)以瞄准点为中心,以正北方向为y轴,垂直于y轴方向为z轴,建立直角坐标系。

2)在yoz坐标系内,拟合目标轮廓曲线,用不等式组表示出目标区域。

3)初始化种群:

②初始化更新速度v0,约定其为初始粒子平均间距除以2。如在0～2π范围内选取时,v0=π/20;在0～π/2范围内选取时,v0=π/80;

③w采用线性迭代策略,即利用式(7)计算。可令最大迭代次数imax=10,所以w0=0.9-(0.9-0.5)·i/10=0.9-i/25=0.9;

4)将当代个体的历史最优pid设为初始α[20]位置,群体的历史最优值pgd设为α[20]中的最佳位置。

5)根据弹着点散布规律,利用蒙特卡洛模拟法[6]计算各粒子的适应度,具体方法如下:

①摸拟每个粒子N次弹着点散布(根据实际情况确定,N越大,模拟精度越高,但计算速度越慢),算出每次导弹的落点坐标(y,z),计算公式[1]为:

(9)

②统计每个粒子的弹着点处于目标轮廓曲线内的个数Mj,则此时的导弹命中概率pj=Mj/N,pj即为第j个粒子的适应度。

6)如果该粒子当前的适应度比其历史最优值要好,那么历史最优pid被当前位置所替代。

7)如果该粒子当前的适应度比历史全局最优值好,那么全局最优pgd被该粒子位置所替代。

8)按照式(6)～式(8)更新每个粒子的速度和位置。

9)判断是否达到停止条件:

①若i≤imax,返回步骤5);

②若i>imax,则迭代完毕,输出粒子全局最优位置和适应度,输出值即为最佳射击方位角和此时导弹的命中概率。

流程如图3所示。

图3 粒子群法搜索最佳射击方位角

2.4 最佳发射阵地选取

在导弹实际作战中,可供选择的发射阵地数量有限,假定有K个发射阵地可供选取,从K个阵地里选出命中概率最大的那个即为最佳发射阵地,即:

(10)

式中:αi表示第i个阵地的发射方位角;pi表示命中概率,pi可通过公式(矩形目标)或蒙特卡洛模拟法计算,最终筛选出使导弹命中概率最大的发射阵地。

3 实例计算

文中选择长宽分别为50.82 m、9.6 m的赵州桥和长宽分别为15 m、13 m的指挥所为实例射击目标。现利用落点服从参数为δy=5、δz=3、r=0.3椭圆散布的某型弹道导弹进行打击。根据式(5),在Matlab7.1软件环境下,编程计算命中概率与射击方位角的对应关系。针对几组特殊的角度,计算出的概率值如表1。

表1 命中概率与射击方位角关系

表1验证了射击方位角对导弹命中概率构成影响,合理选取射击方位角可增大导弹的命中概率。

在不考虑弹着点系统误差及相关系数r情况下,以0.08 rad为步长,在方位角0～π/2范围内,利用式(5)遍历计算导弹对赵州桥、指挥所的命中概率,耗时348 s,画出图4中实线、虚线部分;然后采用粒子群搜索算法,在方位角0～π/2范围内搜索针对指挥所的最佳射击方位角,耗时2 870 s,搜索轨迹如图4中竖线所示,最终输出的最佳射击方位角为0.398 6 rad,此时命中概率为0.863 5。

图4 射击方位角与命中概率关系

1)从图4可以看出,打击长宽比较大的赵州桥时,射击方位角对命中概率影响较大。在0 rad处,命中概率最大,为0.890 4;随着角度的增大,命中概率逐渐减小,在1.3 rad处,达到最小,为0.653 4;最大与最小概率相差0.237。由此可见对大长宽比目标,合理选取射击方位角能大幅度提高导弹命中概率,且角度为0时(弹着点散布椭圆长轴与矩形目标长轴方向一致,即轴向射击)满足条件;而对于小长宽比目标,射击方位角对命中概率影响相对较小。

2)需要特别指出的是,打击长宽比较小的指挥所时,从0 rad开始命中概率随角度的增大而增大,在0.398 6 rad时达到最大,随后减小。由此可看出对于小长宽比矩形目标,简单的选择轴向射击并不能达到最大命中概率。合理化的解释为:当椭圆分布的长轴方向与矩形目标区域的边成某一夹角时,散布椭圆与该目标的“接合”程度最高,此时概率密度的积分达到最大,该角度即为最佳射击方位角。

3)由图4中竖线可以看出,粒子群算法的搜索速度先快后慢,在最优位置附近搜索跨度逐渐缩小,算法具有较好的收敛性。公式遍历筛选和粒子群算法搜索得到的最佳射击方位角相差比较小,两者互相验证,提高了方位角选取结果的可信度。

4 结束语

1)从实用角度而言,对于大长宽比目标,直接采取轴向射击方案可获得最大的命中概率;对于小长宽比目标,利用文中的两种方法都能搜索出最佳射击方位角;而对于一般面目标,只能采用粒子群搜索算法选取。

2)从射击方位角的选取方法上讲,公式遍历筛选与粒子群搜索算法的不同之处在于:前者只适用于矩形目标,而后者能搜索出针对所有面目标的最佳射击方位角;前者具有严密的推理论证,结果更具说服力,而后者计算概率时采用蒙特卡洛模拟法,搜索结果的可靠性受到模拟次数影响;前者运算速度快,因此可选取充分小的步长,使遍历筛选结果满足精度要求,而后者运算速度较慢。

[1] 李新其, 谭守林, 唐保国. 射向变化对跑道失效率的影响分析 [J]. 弹道学报, 2006, 18(2): 84-87.

[2] 李邦杰, 王明海. 基于弹着点椭圆散布的矩形目标命中概率计算 [J]. 火力与指挥控制, 2005, 30(增利): 82-85.

[3] 邱成龙. 地地导弹火力运用原理 [M]. 北京: 国防工业出版社, 2001.

[4] Kennedy JEberhart R C. Particle swarm optimization [C]∥Proc of the IEEE International Conference on NeuralNetworks. Pisca-taway, NJ: IEEE Service Center, 1995: 1942-1948.

[5] Shi Yuhui, Eberhart R C. A modified particle swarm optimizer [C]∥Proc of the IEEE International Conference on Evolutionary Computation. Piscataway, NJ: IEEE Service Center, 1998: 69-73.

[6] 杨世荣, 王才宏, 李小强. 子母弹椭圆散布模型的建立与仿真 [J]. 战术导弹技术, 2008(4): 57-61.

Firing Azimath Selection Based on Ellipse Dispersion of Impact Point

WANG Lian1,XU Weichang1,LI Yongfeng1,LIU Jifang1,Zhang Gaoyu2

(1 College of Sergeant Occupation Technology Education,The Second Artillery Engineering University, Shandong Qingzhou 262500, China; 2 No.96451 Unit, Jilin Baishan 135200, China)

Based on ellipse dispersion of ballistic missile point, a model selecting of the hit probability was. As rectangular target, the best can be directly selected out through formula traversal screening. As common target, particle swarm optimization (PSO) algorithm searching the best. The results of calculation showthat:as larger aspect ratio target, it could be directly to maximize hit probability by axial shooting. As smaller aspect ratio target and general area target, it could get the best by making use of formula traversal screening and PSO algorithm.

ellipse; formula traversal screening; PSO algorithm

2014-04-25

大学科研基金资助

王立安(1987-),男,安徽安庆人,硕士,研究方向:导弹总体性能指标论证与评估。

TJ761.3

A