装填参数对大口径中心爆管式子弹抛撒速度影响*

刘静敏,姚文进,王晓鸣,吴 巍

(1 南京理工大学智能弹药技术国防重点学科实验室,南京 210094;2 63863部队,吉林白城 137000)

装填参数对大口径中心爆管式子弹抛撒速度影响*

刘静敏1,姚文进1,王晓鸣1,吴 巍2

(1 南京理工大学智能弹药技术国防重点学科实验室,南京 210094;2 63863部队,吉林白城 137000)

为研究大口径子母弹的抛撒机理,探讨了中心爆管式子母弹抛撒的几何模型;根据其结构特点,提出了燃气做功时子弹推力面积修正系数的计算方法,建立了内弹道抛撒模型并进行数值仿真,获得燃气压力、子弹速度和子弹加速度等内弹道性能曲线,采用正交试验法分析了抛撒药装药量、中心管炸裂压力及中心管药室容积对子弹抛撒速度的影响,结果表明中心管炸裂压力是最敏感的的影响因素,为中心爆管式大口径子母弹抛撒机构设计提供了依据。

大口径子母弹;中心爆管;内弹道;抛撒模型;抛撒速度

0 引言

现代战争中,子母弹式战斗部越来越成为各国研制的重点[1]。子弹数较多,弹径较大时,多采用径向裂开的开仓方式。径向开仓方式现多采用气囊式抛撒和中心爆管式抛撒。王浩、王帅对气囊式抛撒方式进行了抛撒模型建立及计算仿真[2-3],但针对大口径子母弹,采用气囊式抛撒,气囊设计和强度设计都是非常困难的,且子弹的运动规律也难以预料[4];而中心爆管式结构简单、动作可靠,适合多子弹的大口径子母弹使用,因此大口径子母弹选择中心爆管式抛撒方式。

中心爆管式抛撒机构抛撒动力来源有火药燃烧和炸药爆炸。后者又称为爆炸抛撒,李金柱、蒋建伟等针对爆炸式抛撒进行了数值模拟和子弹散布研究[5-6],但采用爆炸抛撒,子弹所受冲击过载较大。因此文中选

用火药燃烧作为抛撒动力。王浩对中心爆管式火药燃烧抛撒方式进行了抛撒模型的建立及计算仿真[7];郭锦炎还对中心爆管式抛撒方式不同层子弹的运动进行了动力学分析[8],但前人并没有对影响子弹抛撒速度的具体因素进行详细分析。文中针对大口径中心爆管式子母弹进行结构设计和数值仿真,通过正交设计法研究了抛撒药装药量、中心管炸裂压力及中心管药室容积等因素对子弹抛撒速度的影响,为实际工程应用提供参考。

1 几何模型

1.1 结构示意图

大口径中心爆管式子母弹结构简单,主要由母弹外壳、外托架、子弹、内托架、中心管及点火室构成,示意图如图1所示。

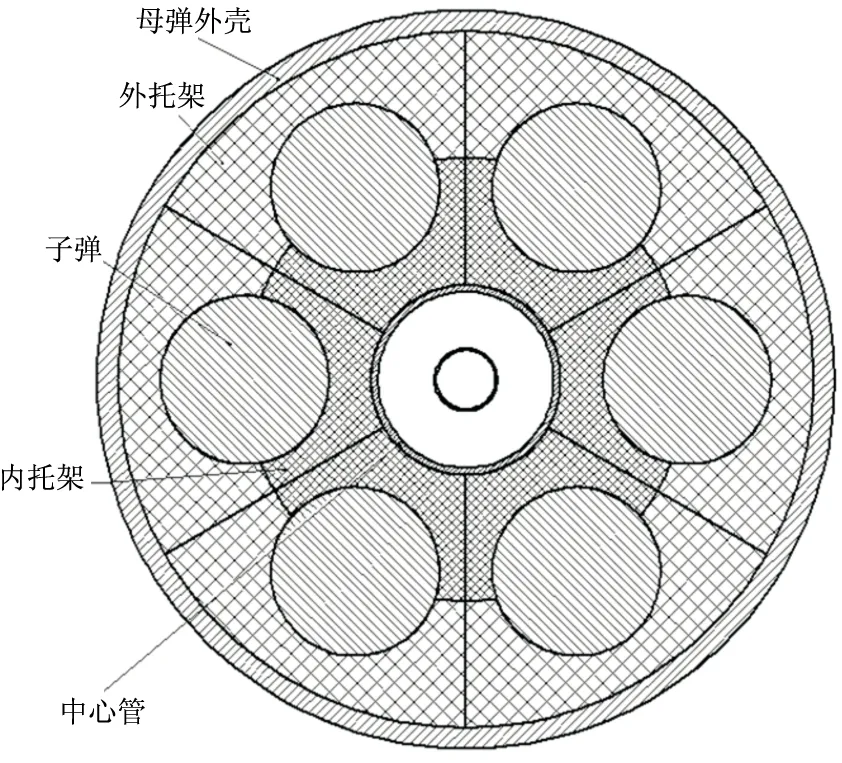
图1 子母弹模型横剖面图

1.2 工作原理

当点火室内点火药被点燃后产生高温高压气体,点火室内燃气压力上升,并作用到传火管上传火孔的限压膜片上,当燃气达到一定压力时,燃气冲破传火孔的限压膜片,点燃中心管内的抛撒药。中心管内抛撒药燃烧释放高温高压气体,压力作用在中心管上,当压力达到中心管炸裂压力时,中心管炸裂。这一时期称为定容燃烧时期,子弹相对于母弹没有运动。

中心管炸裂后,高温高压气体作用在内托架上,将子弹压向外托架进而压向母弹外壳,母弹外壳在所受内压下由于应力集中在沟槽处破裂。子弹解除约束后,在高温高压燃气作用下沿径向向外运动。这一时期称为增容时期,子弹相对于母弹开始运动。

抛撒药燃气压力会随着运动距离的增加及对子弹做功消耗能量而急剧下降,当燃气压力达到大气压力时,抛撒药燃气停止对子弹做功,子弹达到初始分离状态。工作流程示意图如图2所示。

图2 工作过程示意图

2 内弹道数学模型

2.1 基本假设

子弹抛撒过程由抛撒药燃烧,中心管炸裂,母弹外壳破裂,子弹运动等各种物理化学现象构成。此过程火药的化学能转换成子弹的动能,建立数学模型时需着眼于能量守恒。子母弹抛撒过程是复杂的,建立数学模型需提出一些符合实际内弹道过程的基本假设,即抛撒药燃烧服从几何燃烧定律、抛撒药燃气服从诺贝尔方程,燃气流动为等熵流动,气流速度沿径向线性分布、母弹外壳开裂为瞬间完成且子弹托架及母弹外壳在子弹运动过程中由于气流的影响很快脱离子弹,不考虑其破坏情况,子弹的抛撒速度方向仅为沿母弹径向的一维运动等。

此外子弹运动过程中对子弹的推力面积用推力面积修正系数进行修正;子弹在轴向隔板之间运动克服摩擦阻力所做的功,抛撒药燃气对子弹托架及母弹外壳所做的功可用次要功修正系数进行修正;燃气在子弹间和两端面的流失用气体混合物修正项进行修正。

2.2 数学模型

2.2.1 定容时期

这一时期,抛撒药燃烧,中心管内压力迅速上升。由诺贝尔方程推导得抛撒药气体状态方程:

(1)

式中:p为中心管内的平均压力;V0为中心管的容积;w为抛撒药的质量;ρ为抛撒药的密度;α为抛撒药的火药余容;f为抛撒药的火药力;f1为点火药的火药力;w1为点火药的质量;ψ为燃烧质量百分比。

2.2.2 增容时期

这一时期,中心管破裂,子弹开始运动,燃气对子弹做功及燃气流失,压力迅速下降。

1)能量守恒方程

(2)

式中:Ef为考虑气体混合物流失的修正项;θ为绝热指数;R、h为弹后圆柱体的半径和高;φ为除火药气体运动功以外的次要功修正系数;m为子弹的总质量;v为子弹运动速度。

2)子弹运动方程

(3)

式中:s1为压力作用的推力表面积;φs为推力面积修正系数;pb为子弹弹底压力;φ1为虚拟质量系数;m为子弹的总质量,v为子弹运动速度。

3)弹后压力方程

根据内弹道学上的拉格朗日假设,设子弹运动过程中某一瞬间距中心轴距离为r,速度为v,任取微分单元的质量dw,气流速度为vr,作用在r+dr截面上的压力为pr+dpr。以微元单元建立微分方程:

(4)

弹后空间火药燃气与未燃尽火药固体的质量分布是均匀的,所以有:

(5)

由气流速度线性分布得:

(6)

由式(3)～式(6)进行推导,可得:

(7)

积分式(7),得:

(8)

当r=R时,即弹底位置,这时压力就等于弹底压力pb,pr=pb,则平均压力为:

(9)

4)推力面积修正系数及混合气体流失的修正项的确定

由所设计的结构,子弹运动过程中实际推力面积为2πr1h,故推力面积修正系数取:

式中:r1为中心管初始直径;2πRh为压力作用的推力表面积s1。

混合气体流逝的修正项按假设可取:

5)燃速定律、形状函数和子弹速度公式

(10)

式中:z为抛撒药的相对已燃厚度;u1为抛撒药的燃速系数;e1为抛撒药弧厚度的一半;p为中心管内的平均压力;n为抛撒药的燃速指数,χ、λ、μ依据火药的形状和尺寸来定,称为火药的形状特征量。

3 计算结果和分析

3.1 计算结果

由式(1)～式(3)、式(9)、式(10)组成的方程组,采用上述设计的抛撒机构参数,用具有四阶精度的龙格-库塔法进行计算,得到抛撒内弹道曲线,如图3所示。从图中可以看出,4.9 ms前燃气为定容燃烧,4.9 ms时中心管炸裂,母弹同时破裂,子弹开始运动,速度逐渐增大;9.2 ms时子弹达到最大抛撒速度,达到初始分离。由计算结果可以看出上述抛撒机构及数学模型的合理性。主要装填参数和计算结果见表1、表2。

图3 计算结果曲线

表1 主要参数

表2 计算结果

3.2 分析讨论

在进行子母弹特性研究时,子弹初始抛撒速度是重要考虑因素。可采用正交试验法研究抛撒药装药量、中心管炸裂压力及中心管药室容积对子弹抛撒速度的影响。

3.2.1 正交试验设计

正交试验法是研究多因素、多水平的一种优化设计方法。对于本数值模拟试验研究选用3个试验因素即抛撒药装药量、中心管炸裂压力和中心管药室容积,每个因素均为4水平。

确定了上述3因素和各自的4个水平之后,可选择L16(45)正交表进行试验,试验搭配方案见表3,表3最后一列为各自方案下得到的子弹初始抛撒速度。

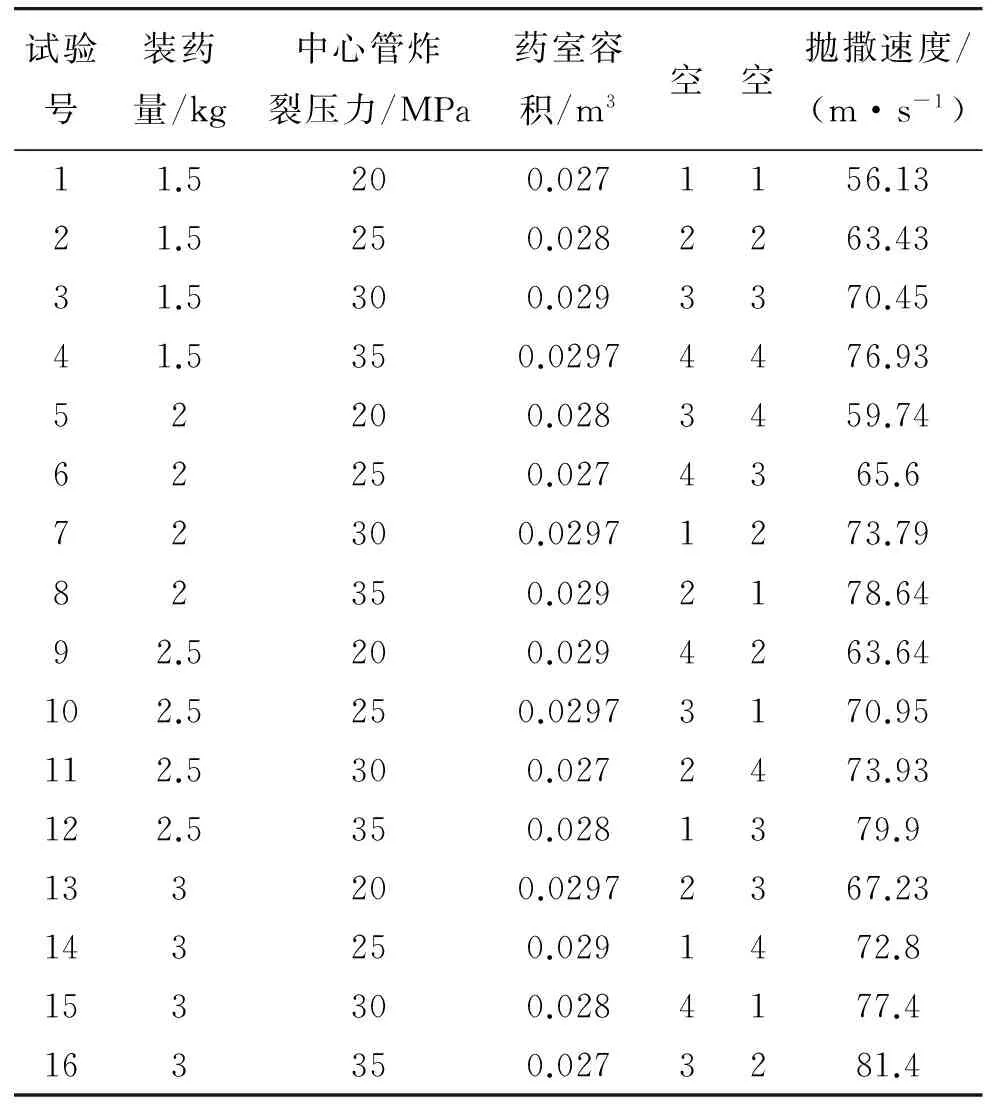
表3 正交试验设计

3.2.2 正交试验结果分析

1)计算各因素水平试验结果平均值

因素水平试验结果之和kij表示第j个因素(j=1,2,3,4,5)、第i水平(i=1,2,3,4)试验结果之和。各因素水平试验结果之和列于表4的1到4行,其平均值列于5到8行。表中因素1为抛撒药装药量,因素2为中心管炸裂压力,因素3为药室容积。

表4 试验结果之和与平均值

2)计算各因素的偏差平方和

因素j(j=1,2,3,4,5)因为水平改变而引起的差异Sj即为因素j的偏差平方和,可由下式计算:

(11)

表5 各因素偏差平方和

因素1、2、3、4、5的水平数为4,其自由度均为3,空白列4、5两项合并一起作为随机误差项,即:

Se=S4+S5=0.372

(12)

误差项偏差平方和Se的自由度为:

fe=3+3=6

(13)

3)因素显著性检验

要校验因素的显著性,首先需要计算它们的F值,由公式:

(14)

求得各个因素的F值,结果如表6所示。

由F检验分布表可查得:当显著性水平α=0.05时,F检验临界值F0.05(3,6)=4.76。各因素的显著性检验结果如表6所示。

表6 正交试验方差分析结果表

由表6分析可知:因素2高度显著,其他两因素显著。即中心管炸裂压力对子弹初始抛撒速度起主要影响作用。从理论上分析,抛撒药装药量的增加实际上就是火药气体总能量的增加,装药量增加,子弹抛撒速度增大,但随着装药量的增加,中心管炸裂时,抛撒药已燃相对量减小,抛撒药利用率较低;中心管炸裂压力增大后,抛撒药在第一时期的燃烧就会更加充分,已燃相对量增大,火药燃烧速度一定的情况下,达到中心管许用压力的时间会增加,火药燃烧时释放的总能量也会增加,子弹的抛撒速度就会增加;中心管药室容积增大,抛撒药燃烧量增多,达到中心管炸裂时间增大,对子弹做功增多,子弹抛速增大。进行子母弹抛撒机构设计时,可以合理考虑这三种因素,找出最佳组合方式,但在考虑子弹抛撒速度的情况下,也要考虑子弹所能承受的过载。

4 结论

1)采用上述大口径子母弹抛撒的数理模型进行数值仿真,仿真结果较为符合规律性。

2)通过正交设计分析,可以看出中心管炸裂压力的变化对子弹抛撒速度的影响更为明显,这为中心爆管式子母弹的结构设计和装药设计提供了参考依据。

3)对于大口径子母弹抛撒,中心爆管式抛撒方式结构简单、易于设计,对于装配末制导子弹的子母弹,可通过控制中心管炸裂压力与抛撒药装药量来控制子弹所承受的最大过载,使其在要求的范围内,同时又能满足其他抛撒指标。

[1] 王军强. 通用子母弹箱开舱过程与数值模拟技术研究 [D]. 南京: 南京理工大学, 2006.

[2] 王浩. 子母弹内燃式气囊抛撒模型及计算机仿真 [J]. 兵工学报, 2001, 22(2): 178-181.

[3] 王帅, 陶如意, 王浩, 等. 子母弹内燃式气囊抛撒内弹道建模及数值仿真 [J]. 弹道学报, 2009, 21(3): 57-60.

[4] 钱华梅. 多用途航空子母弹二次抛撒系统结构设计与计算机仿真 [D]. 南京: 南京理工大学, 2003.

[5] 李金柱, 张庆明, 黄风雷. 子母弹爆炸抛撒的数值模拟研究 [J]. 北京理工大学学报, 2003, 23(增): 186-191.

[6] 蒋建伟, 王丽颖, 门建兵. 中心管爆炸抛撒散布场计算模型及其应用 [J]. 弹箭与制导学报, 2002, (S2): 77-79.

[7] 王浩, 梁世超, 邵志坚. 中心管炸开式子母弹子弹抛撒模型及其计算 [J]. 兵工学报, 1998, 19(4): 301-305.

[8] 郭锦炎, 季晓松, 王浩. 中心爆管子母弹抛撒内弹道过程的数值模拟 [J]. 弹道学报, 2010, 22(2): 62-66.

The Study on the Factors Affecting the Velocity of Submunitions ofLarge-caliber Cluster Munitions

LIU Jingmin1, YAO Wenjin1, WANG Xiaoming1, WU Wei2

(1 Ministerial Key Laboratory of ZNDY, NUST, Nanjing 210094, China; 2 No.63863 Unit, Jilin Baicheng 137000, China)

To study dispersion of large-caliber cluster munitions, the structure model of central tube bursting-type shrapnel was established. According to the feature of the structure, the calculation method of the valid thrust area was built, and an interior ballistic mathematical model was established, the interior ballistic performance curves of this system were got by using a simulation method. Through the analysis of orthogonal experiment, the influences of charge weight of propellant, the allowable pressure of central tube and the volume of drug room on the velocity of submunitions were got. The result shows that the influence of the allowable pressure of central tube on the velocity of submunitions is more. This can provide basis for constructional design of large-caliber cluster munitions.

large-caliber cluster munitions; centralize blast tube; interior trajectory; dispersing model; dispersing speed

2014-03-21

刘静敏(1989-),女,河南漯河人,硕士研究生,研究方向:子母弹抛撒。

Tj413.3

A