真空助力器壳体铆接螺栓分布压力的计算

蔡国震， 张心明

（长春理工大学 机电工程学院，长春130022）

0 引言

真空助力器前后壳体通过螺栓分别与制动主缸、车架相连，螺栓与壳体采用铆接的方式相连。铆钉根部为圆台状，在冲压工程中，冲模挤压圆台上沿，圆台被墩粗，挤压铆钉孔壁，扩张板孔，圆台上沿在冲模的挤压下向外扩展，形成圆锥体铆钉帽。由于真空助力器前壳体与真空源相连，承受大气压力与助力盘回位弹簧所产生的往复力，因而前壳体铆接处设有衬板以加强前壳体的强度。在真空助力器的疲劳寿命实验中，疲劳裂纹均产生于前壳体铆钉孔周围，因而本文以前壳体为例进行分析计算，后壳体无衬板且受力较小，前壳体的分析计算方法完全适用于后壳体。

在以往对真空助力器前后壳体进行有限元分析计算时，将壳体与铆钉螺栓作为一个整体来处理，这样得出的壳体强度和疲劳寿命比实际的要大。因此分析计算铆接螺栓对铆钉孔的分布压力，在对真空助力器壳体进行有限元分析计算时，在铆钉孔的圆柱面上加分布压力载荷，然后再进行有限元分析计算，所得到的计算结果将更加接近实际情况。

1 施铆阶段铆接压力最大时的受力和变形分析

铆接螺栓分布压力需要分两个阶段来分析，在施铆阶段和铆接完成后铆钉孔壁的分布压力是不同的，在施铆阶段铆钉杆被墩粗，发生塑性变形，对孔壁的压力较大。在冲模离开铆钉时，铆钉杆和铆钉孔发生弹性回复，孔壁受到的压力减小。

铆接螺栓与壳体和衬板铆接的部分可以近似看成沉头铆钉，铆接螺栓的根部圆台在冲模的冲压下成圆形向外扩展，最终变为圆锥形铆钉帽，与沉头铆钉相似，如图1所示。

图1 真空助力器壳体螺栓铆钉和典型沉头铆钉

与典型沉头铆钉不同的是，沉头铆钉预制圆锥形铆钉头，沉头铆钉在冲压过程中沉头端的顶铁不动，另外一端的顶铁向下运动冲击铆钉杆形成圆盘状墩头。而铆接螺栓冲压过程中，预制圆盘状铆钉头，这一侧的顶铁不动，铆钉杆在冲模的冲击下形成圆锥状墩头，因此计算铆钉螺栓的分布压力以冲压形成圆锥状墩头一侧为对象。

图2 铆钉飞边宽度和高度

1.1 铆接压力的计算

将铆钉螺栓与真空助力器壳体铆接部分看作铆钉，忽略螺栓杆，如图2所示。

铆钉在冲模的冲压下形成铆钉帽的过程可以作为圆盘类零件的模锻过程。铆钉的铆接压力可以用锻造力计算公式来计算：

式中：σs为屈服极限，MPa；b 为锻造时飞边宽度，mm；h为飞边高度，mm；Fb为飞边面积，mm2；Fd为锻件本体投影面积，mm2；d 为锻件直径（铆钉直径），mm。

与典型铆钉铆接不同，铆接螺栓杆在铆接过程中，仅铆钉根部圆台上沿受到冲模冲击产生变形，如图3所示。

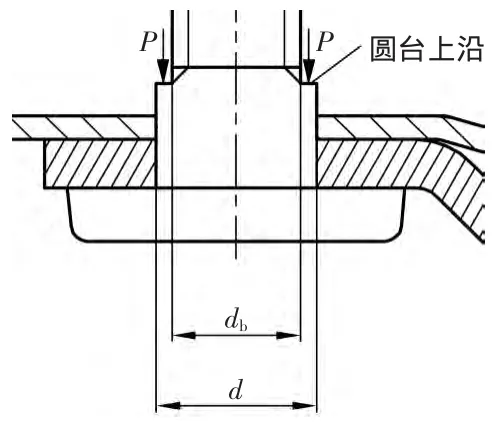
图3 冲模冲压方向

铆钉直径d为圆台直径，锻件本体投影面积Fd为圆台上沿（圆环）面积，即铆钉直径d与螺栓杆直径db之差

铆钉材料为35钢，取σs=350MPa；经实际测量b=2mm，h=0.5 mm；d=10 mm，db=8 mm；Fb=π103.67 mm2］=28.27 mm2。代入式（1），得P=183.07 kN。

如图4所示，设铆钉轴线为Z轴，Z方向上的轴向应力为σ3，设与Z轴垂直的平面内X、Y轴方向上的径向应力分别为σ1和σ2，则距轴线x处的应力为

在铆钉孔壁上 x=0.5d，代入式（2）得 σ3=-1 925 MPa。

图4 铆接压力最大时铆钉的受力状态和铆钉杆中一点的应力、应变状态

由于铆钉为圆柱体，所以σ1=σ2，再由塑性屈服条件σ1-σ3=σs，可得 σ1=σ2=σ3+σs=-1 575 MPa。因此，在铆接力最大时，铆钉孔壁上的分布压力为P2＝σ1=1 575 MPa。

1.2 铆接压力最大时铆钉的应力、应变分析

在冲模下压过程中，铆钉螺栓根部的圆台上沿被冲模向下挤压相对螺纹杆进行剪切运动，此时铆钉杆被墩粗，钉孔被胀大。当铆接孔被压缩到一定程度，金属向下流动的阻力过大，在钉孔内的铆钉直径无法继续增加，在钉孔外的铆钉将向外扩张，并且在冲模的作用下，向斜下方挤压上板面形成铆钉沉头。因此，在铆钉头形成之前，铆钉孔的胀大量已接近极限，在计算钉孔被胀大量时，可以忽略铆钉帽飞边对板材的压力，而将钉孔被胀大视为孔壁受到均匀压力p=p2的无限域开圆孔。钉孔壁的径向位移可用下式计算：

式中：p为作用在铆钉孔圆柱面上的径向分布压力；r为铆钉孔的半径；E为板材的弹性模量；ν为板材的横向变形系数；钉孔壁的径向位移即为铆钉半径的增加量，ur=2△r。

取p=p2=1 575 MPa，r=10 mm，钢板的弹性模量一般在200～210 GPa之间、泊松比一般在0.28～0.3之间，取E=200 GPa，ν=0.3。代入公式（3），得 ur=0.102 75 mm。

2 铆接完成后分布压力的计算

当冲模抬起，离开铆钉后，由于铆接孔直径变小铆钉径向受到挤压，此时Z轴方向上由于板材厚度的恢复，铆钉受到Z轴方向的拉力。在二者共同作用下，铆钉先发生塑性变形，当（σ1-σ3）<σs时，铆钉再发生弹性变形，铆钉长度增加，直径减小。

图5 铆接力最大时板材厚度压缩量

在铆接力达到最大时，由于冲模的冲压，铆钉孔附近与冲模接触区域的板材被挤压变薄，设板材厚度δ减小了△δ，如图5所示。

式中：d为铆钉部分的直径；db为螺纹杆的直径；l为铆钉部分的长度。

取l=6.3 mm，代入式（4），得 V=178.13mm3。

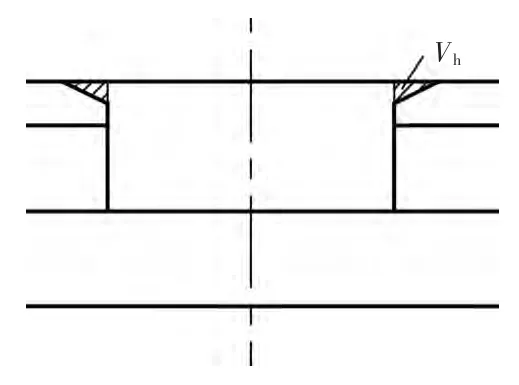
图6 飞边部分的体积

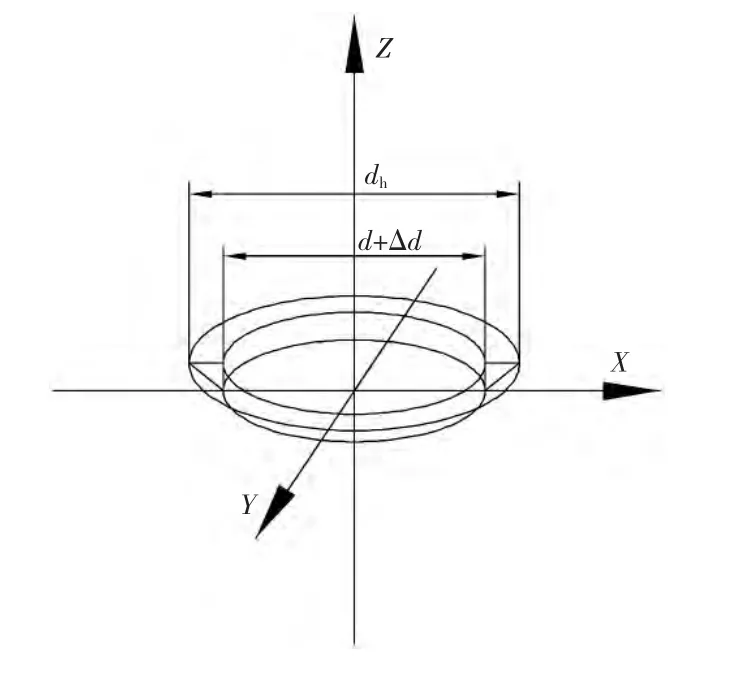
图7 飞边形状

设冲压形成的铆钉沉头飞边（截面为三角形的圆环）体积为Vj，如图 6 所示，飞边高度为h，飞边外沿的直径为dh，如图7所示建立直角坐标系。

式中：S为圆环面积；△d为铆接压力最大时铆钉的直径增加量，△d=2ur；dh为飞边外沿直径，dh=d+△d+2b。

取铆接后的顶杆长δ=5 mm，代入式（6），得铆接力最大时板材厚度压缩量△δ=0.053 3 mm。

为了使制动主缸螺纹孔端面更好地与助力器接触，在铆接完成后，要保证铆接孔周围的板材恢复到原厚度。假设板材厚度恢复到δ，铆接孔直径恢复到d。则铆接完成后，铆钉和板材之间存在Z轴方向和径向的分布力。

如图8所示，设Z轴方向上的应力为σ1，应变为ε1′；径向应力为 σ2、σ3，径向应变为 ε2′=ε3（′ 铆钉为圆柱体），则

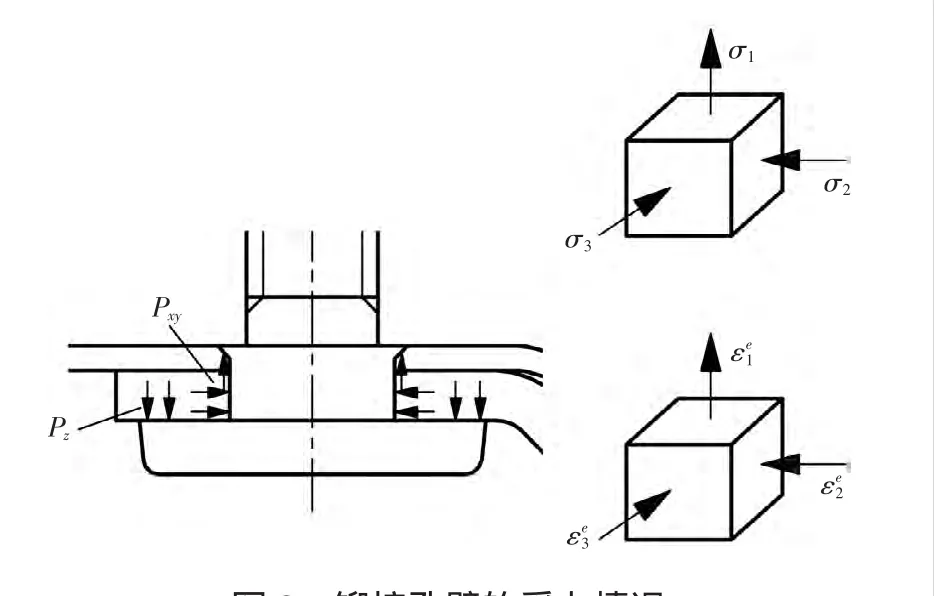
图8 铆接孔壁的受力情况

μ为铆钉的横向变形系数,即铆钉材料的泊松比，取螺栓材料的横向变形系数 μ=0.28。联立式（7）、式（9）和式（8）、式（10）可得：

在铆接压力达到最大之后，铆接孔壁挤压铆钉、板材拉伸铆钉，使得铆钉先发生塑性变形再发生弹性变形，因此满足塑性屈服条件，（σ1-σ3）<σs。 （13）

联立式（11）、式（12）、式（13），解得：σ1<237 MPa，σ2=MPa，因此，铆钉沉头对板材的分布压力为pz=65 MPa，铆接孔壁圆柱面上的分布压力为pxy=σ2=σ3<113 MPa。

3 结语

通过以上计算得到的Z轴方向分布压力Pz和铆接孔壁圆柱面上的分布压力Pxy的数值是分布压力上限。因为分布压力的大小受到很多其它因素的影响，铆钉材料的塑性和均匀性、铆接孔壁的表面质量等因素对分布压力均有影响。在进行有限元分析计算时，应取比理论计算得到的分布压力略小的数值。

由铆接压力的计算公式（1）可知，铆接时所需的压力大小主要受铆钉直径d和铆钉材料的屈服强度σs影响，因此，在选择铆钉机型号时主要参考铆钉直径和材料。

由式（11）、式（12）、式（13）可知，铆接孔壁圆柱面上的分布压力受铆钉材料影响较大，与铆钉直径大小关系不大。Z轴方向分布压力即为铆钉对上下板材的紧固力，其主要取决于铆钉的直径和铆钉材料。因此，如果需要增加上下板材的紧固力大小，可以通过选择较大直径的铆钉或者采用更高强度的材料制造的铆钉，但是需要注意的是，如果选择高强度材料的铆钉，铆接孔壁圆柱面上的分布压力将会增大，这会导致铆接孔附近更易产生疲劳裂纹，铆钉铆接对真空助力器壳体疲劳寿命的影响也将变得更为明显，在有限元分析计算真空助力器壳体疲劳寿命时，考虑铆接的影响意义更大。

［1］ 夏平，刘兰.铆接铆钉分布压力的计算［J］.设备设计与维修，2003（12）：99-108.

［2］ 刘平.铆接变形及其有限元分析［D］.西安：西北工业大学，2007.

［3］ 赵学仁.工程弹性力学［M］.北京：北京理工大学出版社，1988.

［4］ 张洪双.铆接工艺参数分析［J］.机械设计与制造，2011（6）：241-243.

［5］ Q/BQB 403-2003 冷连轧低碳钢板及钢带［S］.