双偏置式万向节钢球径向位移的解析及保持架窗孔的设计

石宝枢

（浙江众达传动股份有限公司，浙江 金华321025）

0 引言

双偏置式万向节，是应用极为广泛的伸缩型等速万向节的一种，该万向节有若干个沿圆周均布的钢球，在其相应的星形套和筒形壳沟道内作同时沿轴向滚动、沿径向移动的复合运动。我们知道，该万向节偏心保持架的作用是：1）夹持钢球；2）引导输入轴（星形套）和输出轴（筒形壳）之间的转角。若钢球在其相应的星形套和筒形壳沟道内沿轴向移动，则偏心保持架每一圆形窗孔的工作宽度（轴向方向）必与相应的钢球直径相等；若钢球在其相应的星形套和筒形壳沟道内沿径向移动，则偏心保持架每一圆形窗孔的直径（径向方向）必大于相应的钢球直径，以确保输入轴（星形套）和输出轴（筒形壳）之间转角时，每一钢球均有足够的活动空间。而如何合理、精确地设计和计算偏心保持架的每一圆形窗孔，要根据双偏置式万向节的结构特征和运动机理，对每一钢球在其相应的星形套和筒形壳沟道内的径向位移量进行系统地解析。

1 双偏置式万向节的结构特征

双偏置式万向节工作部分的结构如图1所示，它主要由与输入轴联结的星形套、与输出轴联结的筒形壳、夹持钢球并引导上述两轴转角的偏心保持架和若干个沿圆周方向均布的传力钢球等组成［1］。

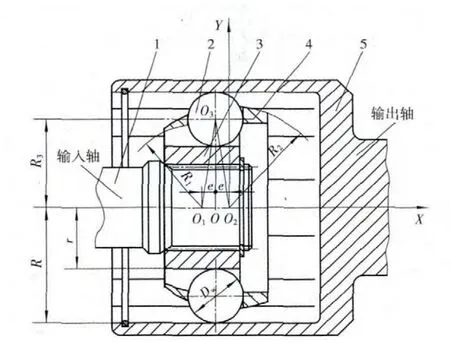
图1 双偏置式万向节的结构

该万向节工作部分的结构特征是：星形套在其外球面上周向均布地设计6～8个与轴线平行且截面形状为关于钢球中心对称的双偏心圆弧形外沟道；同样，筒形壳在其内圆柱面上亦周向均布地设计6～8个与轴线平行且截面形状为关于钢球中心对称的双偏心圆弧形内沟道；用于传力的钢球亦为6～8个；偏心保持架的内球面中心O1、外球面中心O2分别置于其圆形窗孔（即钢球）中心O的两侧，且内球面中心O1、外球面O2至圆形窗孔（即钢球）中心O的距离（称偏心距）相等，即O1O=O2O=e。相应地，偏心保持架亦有相同数量且沿圆周均布的圆形窗孔，用于夹持相应的钢球，偏心保持架每一圆形窗孔沿轴向方向的两侧壁（圆形窗孔的工作宽度）均与相应的钢球过渡配合；偏心保持架的内球面与星形套外球面为较小间隙（0.02～0.06 mm）的间隙配合；偏心保持架的外球面与筒形壳内圆柱面为较大间隙（0.2～0.3 mm）的间隙配合。使双偏置式万向节在输入轴（星形套）和输出轴（筒形壳）同时有一定角位移和轴向位移等复杂工况下，仍能平稳、可靠、灵活、精确地传递运动和转矩。

2 两轴转角时的运动机理

当双偏置式万向节的输入轴（星形套）和输出轴（筒形壳）绕两轴交点转角时，该万向节的运动情形如图2所示。设两轴的交点（偏心保持架的宽度中心）为O，O1O=O2O=e。由于与输入轴联结的星形套和与输出轴联结的筒形壳的沟道素线均为与轴线平行的直线。所以，在一定范围内，O点可沿轴线自由移动。由图1的几何关系立即可得星形套和筒形壳沟道的钢球中心圆半径为：

式中：R为筒形壳沟道底部的圆弧半径，mm；R3为星形套和筒形壳沟道的钢球中心圆半径，mm；r为星形套沟道底部的圆弧半径，mm；Dw为钢球直径，mm。

设输入轴（星形套）绕O点的转角为α，而输出轴（筒形壳）不动。

1）以O2为坐标原点，建立关于输出轴（筒形壳）的平面直角坐标系O2XY；

2）设输入轴（星形套）绕O点转动的转角为α，偏心保持架绕O2顺时针的转角为α1，以O2为坐标原点，建立关于偏心保持架的平面直角坐标系O2X2Y2。

图2 双偏置式万向节两轴的转角

由坐标轴的旋转得［2］

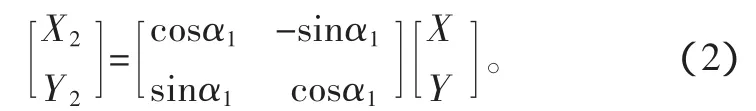
由此，可转化为［3］

3）以偏心保持架的内球面中心O1为坐标原点，建立关于输入轴（星形套）的平面直角坐标系O1X1Y1。

4）设输入轴（星形套）绕O点的转角为α，偏心保持架相对于输入轴（星形套）的转角为α2。以O1为坐标原点，建立关于偏心保持架的平面直角坐标系O1X3Y3。则有

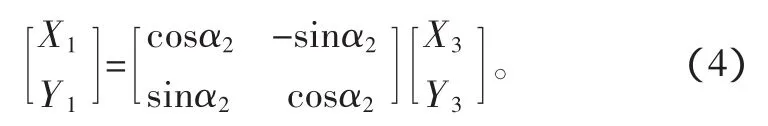
双偏置式万向节的上述各转角间有如下的关系：

设双偏置式万向节沿圆周均布的每一钢球在其相应的星形套和筒形壳沟道内沿偏心保持架的圆形窗孔径向一个方向的位移为d，则某钢球的中心O3在O2X2Y2坐标系中的坐标分别为

该钢球的中心O3在O2XY坐标系中的坐标分别为：

即有：

若双偏置式万向节的输入轴（星形套）绕O点转角为α，此时，偏心保持架绕O1点逆时针的转角为α2，沿圆周均布的每一钢球在偏心保持架圆形窗孔中沿径向一个方向的位移为d，则该钢球的中心O3在O1X3Y3坐标系的坐标分别为

该钢球的中心O3在O1X1Y1坐标系的坐标分别为：

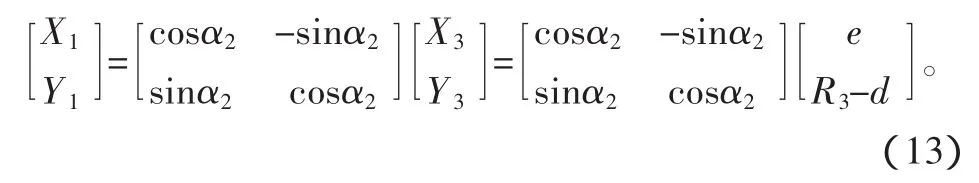
即：

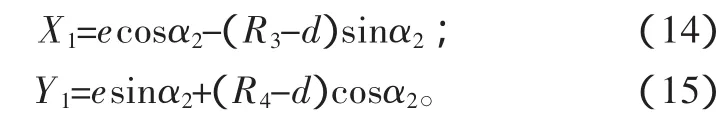
我们知道，双偏置式万向节在其极限转角和极限位移范围内的任何情况下，沿圆周均布的每一钢球均必须与其相应的星形套和筒形壳沟道相切。所以，在这个极限转角和极限位移范围内，该万向节的钢球中心O3至偏心保持架内球面中心O1和外球面中心O2的距离始终相等且保持不变，即O3O1=O3O2。可确保该万向节始终等角速地传递运动和转矩。

由式（9）、式（10）、式（14）和式（15），可分别对 O3O1和O3O2进行求解，即：

由于上述两式相等。显然，必有

则该钢球中心O3至输入轴的距离Y1等于O3至输出轴的距离Y，即

由此可得出结论：双偏置式万向节的偏心保持架的轴线，始终处于输入轴（星形套）和输出轴（筒形壳）两轴夹角的等分线上。换言之，双偏置式万向节若干个沿圆周均布的钢球中心所在的平面，始终处于输入轴（星形套）和输出轴（筒形壳）两轴夹角的等分面上，即双偏置式万向节中偏心保持架的转角始终等于输入轴（星形套）和输出轴（筒形壳）两轴转角的一半。这是双偏置式万向节重要的运动机理（或结构原理）之一。

由式（10）得

即

3 钢球径向位移的解析

根据上述双偏置式万向节的结构特征和两轴转角时的运动机理，可对该万向节沿圆周均布的任一钢球，在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）其中一个方向的位移量进行求解。

由式（19）得

esin（α/2）+（R3-d）cos（α/2）=R3。

又由于R3=D/2（D为星形套和筒形壳的钢球中心圆直径，mm），所以 esin（α/2）+（D/2-d）cos（α/2）=D/2。解之得，双偏置式万向节沿圆周均布的每一钢球在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）一个方向的位移量为

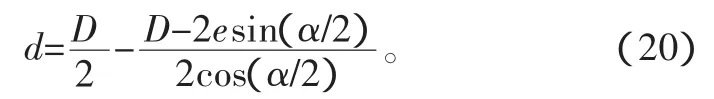
由此得，双偏置式万向节沿圆周均布的每一钢球在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）一个方向的最大位移量为

由于双偏置式万向节的最大转角为输入轴（星形套）相对于输出轴（筒形壳）绕两轴交点沿顺时针、逆时针的两个方向，两轴转角的极限值（即最大转角）为2αmax。

显然，双偏置式万向节的每一钢球在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）两个方向的最大位移总量为

将式（21）代入式（22），得

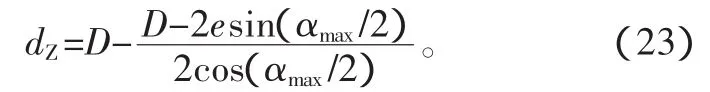
4 偏心保持架窗孔的设计

双偏置式万向节的偏心保持架每一圆形窗孔的典型结构如图3所示，因每一钢球在其相应的星形套和筒形壳沟道内的径向位移量与偏心保持架每一圆形窗孔的几何形状和尺寸密切相关，根据上述的推导，即可对该圆形窗孔进行如下的设计计算。

图3 偏心保持架的窗孔

4.1 圆形窗孔的宽度

我们知道，偏心保持架每一圆形窗孔的轴向方向（窗孔宽度）与各自的钢球为过渡配合，以确保每一钢球在相应的星形套和筒形壳沟道内滚动。所以，偏心保持架每一圆形窗孔的工作宽度与相应钢球的公称直径应相等，即

应当指出的是，该过渡配合的偏差一般为±0.01 mm。所以，每一圆形窗孔的工作宽度B与相应的钢球直径DW配合的间隙为0～0.01 mm；过盈量亦为0～0.01 mm。

通常，偏心保持架的每一圆形窗孔的加工过程为：冲窗孔→铣（或拉）窗孔→磨窗孔。显然，偏心保持架的每一圆形窗孔的宽度B1应是工作宽度B再减去其精加工余量 εB，即

式中，εB=0.7～1.5。

4.2 圆形窗孔的直径

双偏置式万向节在两轴转角时，沿圆周均布的每一钢球，在其相应的星形套和筒形壳沟道内，不仅沿轴向移动，在径向上还要沿偏心保持架圆形窗孔的长度方向移动。显然，每一圆形窗孔的理论直径D0。应等于相应的钢球直径（圆形窗孔的工作宽度）与该钢球在沟道内沿径向两个方向的位移总量之和，即

但是，为使双偏置式万向节沿圆周均布的每一钢球在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）上有足够的活动空间，同时，考虑到偏心保持架圆形窗孔的制造精度，在窗孔直径设计时，亦应有一窗孔直径加大值εD。所以，偏心保持架每一圆形窗孔的直径D1计算公式为

将式（23）代入式（27），得

式中：αmax=23°；εD=0.5～1。

4.3 圆形窗孔的工作长度

前已述及，理论上偏心保持架每一圆形窗孔的直径，包含了夹持钢球的长度（即钢球直径或圆形窗孔的工作宽度），但真正工作时，不含夹持钢球的长度，又考虑到偏心保持架每一圆形窗孔的对称性及制造精度，其工作长度应再加上一窗孔长度加长值εL。所以，偏心保持架每一圆形窗孔的工作长度L计算公式为

式中，εL=1～2。

将式（28）代入式（29），得

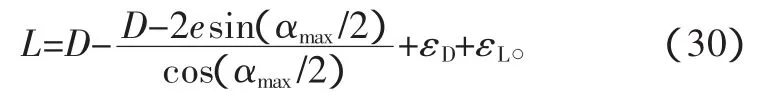
式中：εD=0.5～1；εL=1～2。

5 设计计算举例

某双偏置式万向节，已知的相关参数为：Dw=17.463mm、D＝56.79 mm、e＝4.3 mm、εD＝0.95 mm、εL＝2 mm、εB＝0.8 mm、αmax＝23°。试设计计算该偏心保持架圆形窗孔的各结构参数。

解：将已知的相关参数代入式（24），得该偏心保持架每一圆形窗孔的工作宽度为B＝Dw＝17.463 mm。

将已知的相关参数代入式（25），得该偏心保持架每一圆形窗孔的宽度为 B1＝17.463－0.8＝16.7 mm。

将已知的相关参数代入式（28），得该偏心保持架每一圆形窗孔的直径为

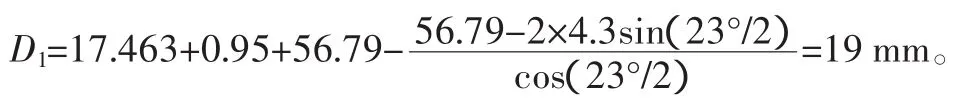
将已知的相关参数代入式（30），得该偏心保持架每一窗孔的工作长度为

6 结语

本文通过对双偏置式万向节输入轴（星形套）相对于输出轴（筒形壳）转角的运动分析，系统、精确地解析出沿圆周均布的每一钢球在其相应的星形套和筒形壳沟道内，沿径向（偏心保持架圆形窗孔的直径方向）的位移量。为合理、精确、创新地设计双偏置式万向节偏心保持架的圆形窗孔，提供了可靠的理论依据。

［1］ 石宝枢．双偏置式等速万向节的结构设计［J］．轴承，2008（8）：6-11．

［2］ 数学手册编写组．数学手册［M］．北京：高等教育出版社，1979．

［3］ 王霄锋．汽车底盘设计［M］．北京：清华大学出版社，2010．