习题引导探究发散演绎精彩
☉浙江省余姚市第二中学 杨福来
习题引导探究发散演绎精彩
☉浙江省余姚市第二中学 杨福来
高考数学命题以“能力立意”为指导思想,更加注重考查考生的基础知识、创新意识和发散思维.很多高考题都来源于书本的例题和习题的改编再创造,我们有必要深入地认识课本中的习题,在课堂中教会学生数学地思考问题,进而培养学生的发散思维,提高学生的能力.
题目直线y=x-2与抛物线y2=2x相交于A、B两点,求证:OA⊥OB.
一、习题分析
本题是人教版《全日制普通高级中学教科书(选修2-1)数学》73页的第六题,主要考查解析几何的基本思想和基本方法,看似平凡,其实是一道可以用来进一步推广方法和技巧的好题,对启迪学生的发散性思维,拓宽学生的解题思路很有帮助.
解析:设A(x1,y1),B(x2,y2).
将直线y=x-2代入抛物线y2=2x得x2-6x+4=0,所以x1x2=4,x1+x2=6,y1y2=(x1-2)(x2-2)=-4.
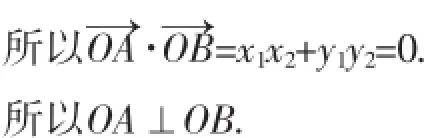
二、习题的推广和挖掘
发散1:A、B是抛物线y2=2px(p>0)上异于顶点的两个动点且OA⊥OB,则:
(1)A、B两点的横坐标之积、纵坐标之积为定值;
(2)直线AB过定点.
证明:(1)设A(x1,y1),B(x2,y2),设直线为x=my+n,代入抛物线得y2-2pmy-2pn=0.
所以y1y2=-2pn,y1+y2=2pm.
又OA⊥OB,所以x1x2+y1y2=

(2)由(1)得直线为x=my+n=my+2p,所以直线过定点(2p,0).
在发散1中,如果改为逆命题,直线过定点(2p,0),同理也可以证明出OA⊥OB.进而我们思考,在上题中直角顶点O是坐标原点,A、B是抛物线y2=2px(p>0)上异于顶点的两个动点,如果把直角顶点移到抛物线上来,可以得到类似的结论吗?
发散2:定点M(x0,y0)在抛物线y2=2px(p>0)上,A、B是抛物线上的两个动点且MA⊥MB,则直线过定点.
证明:设A(x1,y1),B(x2,y2),设直线为x=my+n,代入抛物线得y2-2pmy-2pn=0.
所以y1y2=-2pn,y1+y2=2pm.
又MA⊥MB,所以M→→A·M→→B=0.
所以(x1-x0)(x2-x0)+(y1-y0)(y2-y0)=0.
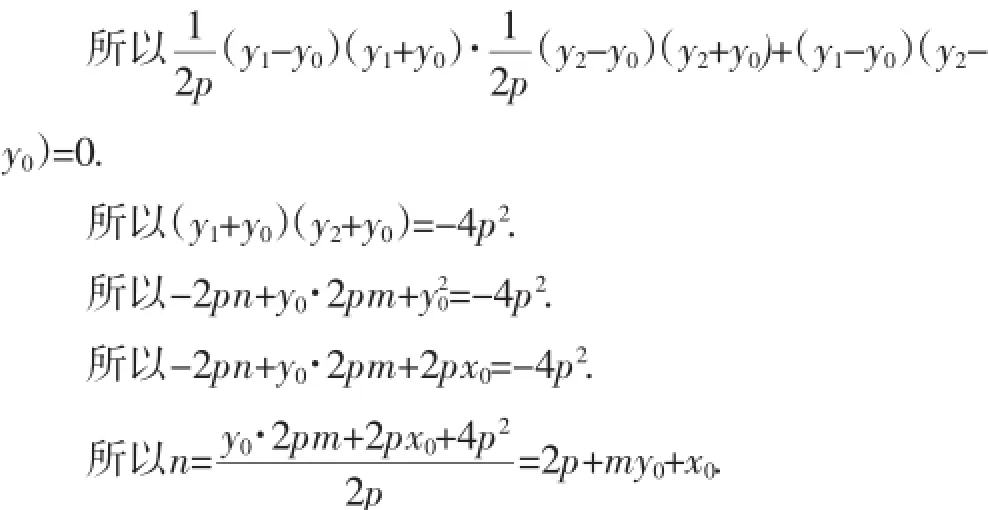
所以直线AB为x=my+2p+my0+x0=m(y+y0)+x0+2p.
所以直线AB恒过定点(x0+2p,-y0).
因此当直角顶点在抛物线上动起来时,也可以得到直线过定点,原来抛物线有这么好的发散结论,所以笔者就在想能不能继续发散,得出抛物线其他的定点定值问题呢?
发散3:抛物线y2=2px(p>0),F为抛物线的焦点.
(1)过抛物线y2=2px(p>0)的焦点弦AB的两个端点作抛物线的切线AP、BP,则两切线的交点P在抛物线的准线上;
(2)过抛物线y2=2px(p>0)的准线上任何一点P作抛物线的两条切线AP、BP,切点为A、B,则直线AB过抛物线的焦点F.
以上两式相减可得(y1-y2)y=p(x1-x2),即(y1-y2)y=代入y1y=-p(x1+x2)中,可得y1y2=2px.
又由发散1类似可得y1y2=-p2,所以即交点P的坐标为
到此通过发散,我们得到了一个关于焦点弦的结论,这也给笔者打开了广阔的思路,笔者尝试着对上题进一步的思考,得到一个变式:过抛物线y2=2px(p>0)的焦点F的一条弦AB,记准线与x轴的交点为E,AE、BE分别交y轴于P、Q两点,求证:线段EF平分角∠PEQ.(提示:事实上只需要证明kAE+kBE=0即可)
事实上,对于变式的思考,我们涉及了抛物线及斜率之和,如果我们进一步发散,可以得到如下结论.
发散4:已知抛物线x2=2py(p>0),F为抛物线的焦点,A、B是抛物线上的两个动点,且在y轴的同侧,如果直线AF的斜率和直线BF的斜率互为相反数,则直线AB过定点.
证明:设A(x1,y1),B(x2,y2),焦点为
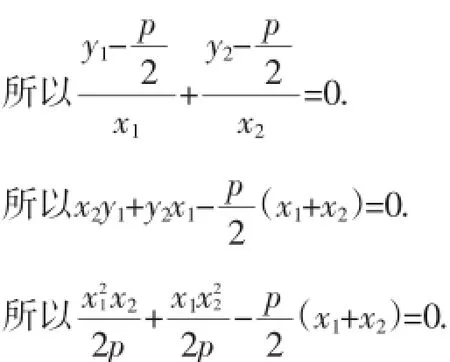
所以x1x2=p2.
直线AB的斜率肯定存在,设直线方程为y=kx+b,代入抛物线得x2-2pkx-2pb=0.
所以x1x2=-2pb.
所以x1x2=p2=-2pb.

三、结束语
高考数学命题以“能力立意”为指导思想,更加注重考查考生继续学习的潜能和基础文化素质,以及创新意维与发散思维.很多高考题都来源于书本的例题和习题的改编再创造,试题的解答不需要高深的数学知识和高难度的变形技巧,而需要有较强的在新情景下解决问题的能力,需要一定的创新意识和发散意识.因此我们有必要重新深入地认识课本中的习题,在课堂中我们要体验学习的过程,理解数学的本质,提高数学素养,学会数学地思考问题,学会对习题的思考发散,提高学生的能力.
1.普通高中课程标准试验教科书数学(选修2-1)[M].北京:人民教育出版社,2006.
2.王恒亮.抛物线定点、定值问题的探究[J].中学数学(上),2013(4).

