解题活动中表征系统的建构与分析
☉江苏省苏州高新区教研室 陈勇☉江苏省苏州实验中学 丁益民
解题活动中表征系统的建构与分析
☉江苏省苏州高新区教研室 陈勇
☉江苏省苏州实验中学 丁益民
从数学解题信息论来看,数学解题的过程就是通过对信息的合适表征,与记忆储存中的相关定理、公式及其推理过程、基本模式(模型)等依据进行同化顺应的心理活动.在解题教学中,教师应引导学生建构合适的表征系统,并针对性地对解题中产生的思维障碍和心理活动进行合适调控与指导.
一、通过系统建构与分析,突破表征受阻
正确表征已有信息是问题顺利解决的关键,很大程度上取决于学生是否真正表征清楚每个信息及信息间的关系.因此,教师应引导学生审读问题中的信息,并对已有信息进行归类梳理,形成表征系统,这样不仅可以迅速帮助学生分析出信息的属性、呈现形式、知识内涵等,而且在学生信息表征受阻时,还可借助表征系统中其他容易表征的经验进行“借鉴”式心理活动.

读题后容易建立信息表征系统:

系统分析:从属性上看,信息1-4属于并列式信息,与信息1和2相比而言,信息3和4由于抽象性较强学生很可能会出现表征受阻,但从表征系统中可知信息陈述方式一致,因此可从信息1和2的表征经验中寻求理解“通道”——将抽象的符号语言翻译成易接受、可操作的自然语言.
信息1表征:f(x)为奇函数→f(-x)=-f(x)→横坐标的关系是互为相反数,纵坐标的关系也是互为相反数;
信息2表征:x1≤x2时,f(x1)≤f(x2)→横坐标增大,纵坐标也增大→f(x)在[-1,1]上单调递增.
从中获取的表征经验是:将符号语言分横坐标、纵坐标翻译成熟悉的数学语言.由此指导信息3和4的表征.
信息4表征:f(x)=1-f(1-x)⇒f(x)+f(1-x)=1→横坐标之和为1,纵坐标之和也为1→函数图像关于对称.
可见,通过建构表征系统能清晰地梳理出信息的表达形式,若能让学生发现信息间“一致”的特征,通过已有表征经验指导相对生疏信息的表征,可以使得难理解的信息逐步明朗化,进而推动解题活动的开展.
二、通过系统建构与分析,确定核心信息
数学题中的信息一开始以零散状态出现在条件与结论中,并且信息之间也有侧重之分,如果以非核心信息为思维起点,那么学生的思维就容易走偏.为了避开干扰信息影响思维方向,通过建构表征系统,可引导学生从中提取出核心信息,并以此为活动中心,聚拢所有信息,逐步把握问题的实质,最终形成条件与目标之间的思维通道.
通过信息系统的建构,对所有信息进行分析,并确定出核心信息.
信息1:定点A(a,a)——尽管信息中出现了目标“a”,但这一信息对整个问题起不到固着支配的作用,处于独立的位置,故不能作为核心信息;
夏季的庐山很热闹。合面街是最繁华的商业街,从合面街到河南路口是单面街。河南路口对面,现在的振豪超市,原是赫赫有名的胡金芳大旅社,门面后背的一大片房屋也属于它。观光客多选择在这里住,临街近,方便。当年的胡金芳大旅社声名远播,生意远胜于仙岩饭店。
通过分析可以看出,表征系统的建构,为核心信息的确定提供了保证,将减少因信息过多造成的信息干扰,对准确表征信息的主要特征,有效缩短思维长度,优化思维品质,起到了积极推进的作用.
三、通过系统的建构与分析,形成思维走向
我们知道,一旦数学问题中信息较多时,则易产生干扰交错的现象,很多学生常常因此出现思维混乱,解答中断.通过建构表征系统,可以理顺信息间的逻辑关系和因果联系,进而帮助学生形成清晰的思维走向.
例3如图1,在平面直角坐标系xOy中,F1、F2分别是椭圆=1(a>b>0)的左、右焦点,顶点B的坐标为(0,b),连接BF2并延长交椭圆于点A,过点A作x轴的垂线交椭圆于另一点C,连接F1C.若F1C⊥AB,求椭圆的离心率e的值.

图1
逻辑结构系统的建立如下所示.对象分析:点F1、F2、A、B、C.
对象间的关系:按照信息出现的先后顺序、生成地位、位置关系,可将其建构成如图2所示的表征系统:
——生成关系:点A是由直线BF2与椭圆相交而得,点C是由过点F1的直线与椭圆相交而得;
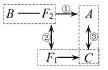
图2
——地位关系:F1、F2与A、C都具有对称性,它们具有同等地位;
——位置关系:直线BF2与直线CF1垂直,直线AC垂直于x轴.
求解目标:求离心率,本质是建立关于a、b、c的齐次方程.
从逻辑结构系统中可见:通过不同关系可以生成不同的思维途径,形成不同的思维走向,并且可以进行思维的评估.
思维走向1:以生成关系为起点
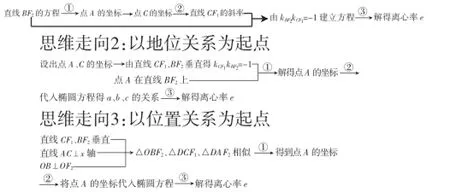
不难看出,通过建构表征系统,不仅错综复杂的信息交叉关系被理顺,而且还可按照不同的起点形成相应的思维方向.
在解题教学中,教师若能放慢节奏,多引导学生深入到问题内部,带领他们建构恰当的信息表征系统,通过细致深入的分析,将有效地提高学生的信息表征能力.
1.罗增儒.数学解题学引论[M].西安:陕西师范大学出版社,2008.

