气容和气阻对脉冲萃取柱柱重瞬间压降信号测量的影响

曾 鑫，李少伟，景 山，刘继连，吴秋林

(1.中国核电工程有限公司 电仪所，北京 100840；2.清华大学 核能与新能源技术研究院，北京 100084)



气容和气阻对脉冲萃取柱柱重瞬间压降信号测量的影响

曾 鑫1，李少伟2，景 山2，刘继连1，吴秋林2

(1.中国核电工程有限公司 电仪所，北京 100840；2.清华大学 核能与新能源技术研究院，北京 100084)

本文从理论和实验两方面对吹气法测量中气容和气阻的影响进行了系统研究。结果表明，气容和气阻对压力波动信号有明显的衰减作用，而对压力波动信号的延迟作用可忽略，随着气容体积的增大和气阻内径的减小，衰减作用增强；气容和气阻组合的衰减作用大于相应的单气容或单气阻，先气阻后气容组合方式的衰减作用大于先气容后气阻的衰减作用；气容和气阻的引入对吹气管出口处的气速影响不大，所以对吹气杯的设计没有影响。本文的理论与实验结果为吹气法中气容和气阻的设计应用提供了基础。

吹气法；气容；气阻；柱重瞬间压降；脉冲萃取柱

吹气法在核燃料后处理行业有着广泛的应用，由于后处理中的脉冲萃取柱内部无法直接观察，吹气法对其内部参数的远距离监测就起到了关键作用。吹气法所能实时监测的参数包括：两相流体密度、柱重、存留分数、脉冲振幅与频率、两相界面位置等，另外吹气法在界面实时控制方面也被成功应用[1-12]。然而对于吹气法，还有一些问题值得更深入研究。由于气体脉冲的存在，吹气法所测得的柱重瞬间压降信号是一近似正弦的曲线，中试厂曾采用气容和气阻方式对吹气法所测量的压降信号进行滤波，以期得到平稳的压降信号[9-12]，但处理效果并没有达到预期要求，而且对气容和气阻的工作原理也没有进行更深入的研究。本工作拟针对气容和气阻对脉冲萃取柱瞬间压降时间序列的影响，采用实验与理论分析相结合的方法，研究气容和气阻对柱重压降信号在线测量的影响，为吹气法在核燃料后处理中的应用提供基础。

1 理论分析

在前期工作中，本研究小组已对吹气管内气体流动与压力波动进行了系统研究[13]，并得到了描述吹气管内压力与流速变化的偏微分方程组，这一方程组也适用于包含气容和气阻的吹气管管路内的流动情况，该方程组为：

(1)

(2)

其中：ρ为气体密度；u为气体的轴向速度；t为时间；x为沿吹气管长度的位置坐标；p为吹气管中任意点的瞬间压力；λ为气体摩擦阻力系数；μ为空气黏度；d为吹气管管径；c为声速。

但加入气容和气阻后，求解的边界条件将发生变化，因此，本文将分别对气容和气阻进行讨论。

1.1 包含气容的吹气管内流动

对于包含气容的吹气管，管段与气容连接处的边界条件可通过假设气容内压力均匀得到，进而进行管段计算，由管段计算结果得到管段与气容连接处的气速，根据该气速即可计算气容的压力变化。由于假设气容内压力均匀，因此在管段与气容连接处有：

(3)

其中：S为管的截面积；V为气容体积。

再根据绝热过程气体状态方程可得：

(4)

结合式(2)，可得到管段与气容连接处的速度与压力的另一关系式：

(5)

要对含气容的吹气管管路的气体流速与压力进行计算，需要确定4个边界条件，即吹气管起始端、气容前端、气容后端、吹气管末端4个位置的边界条件，吹气管起始端和末端的边界条件与文献[13]中无气容和气阻的情况相同，根据式(4)和(5)可确定气容两端的边界条件，最终确定含气容吹气管管路的定解条件：

(6)

其中：xC为气容的安装位置；f和b分别代表气容的前端和后端。用数值方法对式(1)、(2)在定解条件(式(3))下求解，即可得到含气容吹气管测量端(压力变送器)的瞬间压力p和时间t的关系，并进而与实验测量到的瞬间波动信号进行比较。

1.2 包含气阻的吹气管内流动

对于包含气阻的吹气管，对气阻内流动作拟稳态假设，认为气阻内流速均匀，那么气阻内流速uR的变化可用如下方程描述：

(7)

其中：Δp为气阻两侧压力差；lR和dR分别为气阻的长度和内径。

由于气阻内流速与主体管路内流速满足uRSR=uS(SR为气阻截面积)，结合式(1)，可得气阻两侧的主管路内流速与压力的另一关系式：

(8)

要对含气阻的吹气管管路的气体流速与压力进行计算，需要确定4个边界条件，即吹气管起始端、气阻前端、气阻后端、吹气管末端4个位置的边界条件，起始端和末端的边界条件与文献[13]中无气容和气阻的情况相同，根据式(7)和(8)可确定气阻两端的边界条件，最终确定含气阻管路的定解条件：

(9)

其中：xR为气阻的安装位置；f和b分别代表气阻的前端和后端。用数值方法对式(1)、(2)在定解条件(式(9))下求解，即可得到含气阻的吹气管在测量端(压力变送器)的瞬间压力p与时间t的关系，此计算结果可与实验测量到的瞬间压力波动信号进行比较。

对于既包含气容又包含气阻的情况，只要将两种情况的边界条件进行组合，即可求解。

2 实验设备

图1为研究气容和气阻对吹气法测量脉冲柱压力的影响的实验装置图，该设备主要由折流板萃取柱、气体脉冲发生系统、气容和气阻面板和压降测量系统等4部分组成。折流板脉冲萃取柱的柱径D为0.3 m，有效高度Hc为5.6 m(其中不锈钢段高度为4.6 m，玻璃段高度为1.0 m)，板间距H为0.072 m，开孔率为23%，板数为70；脉冲腿内径为0.1 m，脉冲腿玻璃段高度为4.0 m。水作为实验介质，压缩空气通过旋转阀使脉冲柱中液体产生往复脉冲运动，从而在脉冲柱中产生压力波动。吹气杯处的压力波动通过吹气管及气容和气阻面板传播到压力传感器，经数据采集系统实时得到压力数据。同时采集脉冲柱底部、脉冲腿和缓冲罐内压力作为参考数据。由于实验体系为水，所以脉冲柱底部压力直接用压力传感器进行采集。实验中吹气管内径为4 mm，所采用的吹气管长度为17 m。

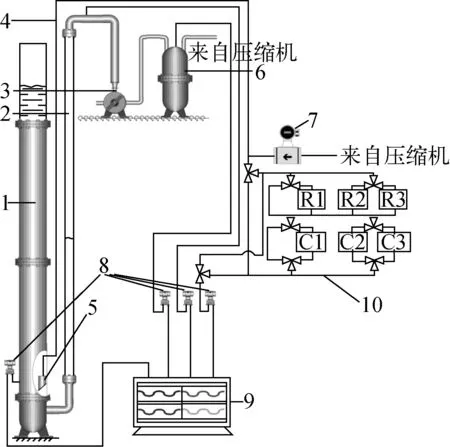
1——脉冲柱；2——脉冲腿；3——旋转阀；4——吹气管；5——吹气杯；6——缓冲罐；7——流量计；8——压力传感器；9——在线数据采集系统；10——气容和气阻面板

气容和气阻实验面板的照片如图2所示，通过调节气容和气阻面板上的三通阀，可实现吹气管管路中不包含气容和气阻、包含单独气容、包含单独气阻、先气容后气阻、先气阻后气容5种模式之间的转换，并可实现3种气容和3种气阻之间的切换，从而通过考察压力数据在不同情况下的变化研究气容和气阻对压力测量的影响规律。3种气容的体积分别为500、800、1 000 mL(气容1、气容2、气容3)；3种气阻均为长60 mm的不锈钢毛细管，内径分别为0.3、0.5、1.1 mm(气阻1、气阻2、气阻3)。由于实验条件较多，为便于后文描述，将不同实验条件进行编号，编号与实验条件的对应关系如表1所列。

图2 气容和气阻实验面板照片Fig.2 Picture of air capacity and air resistance experimental panel

3 结果与讨论

3.1 理论计算结果与实验结果比较

当脉冲频率为1 Hz、脉冲振幅为34 mm时，在1个周期内用理论模型计算的测量端瞬间压力波动时间信号序列与实验测量结果的比较如图3所示。前期研究[13]结果表明，17 m长的吹气管不会使压力波动发生衰减，因此本文在17 m吹气管的基础上加上气容和气阻的组合进行讨论。为方便比较各条件下的压力波动，图3中的数据均减去了时均压力。时均压力在不同气容和气阻条件下变化不大，本实验中时均压力在不同实验条件下的测量偏差不超过±3%，且气容和气阻对时均压力没有明显的影响，因此在本文的实验范围内可认为气容和气阻对时均压力的影响在其测量误差范围内。

由图3可知，在脉冲振幅相同时，理论模型所预测的结果与实验结果是一致的，验证了理论模型的正确性。从图3a可看出，气容对压力波动有明显的衰减作用，随着气容的增大，其对压力波动的衰减作用增大；从图3b可看出，气阻对压力波动也有明显的衰减作用，随着气阻内径的减小，其对压力波动的衰减作用增大，特别是当气阻内径为0.3 mm时，气体压力波动减小到原来的2%以下，几乎可忽略；从图3c可看出，气容加气阻的衰减作用大于单独气容或单独气阻，但经过气容后，气阻的衰减作用较其单独使用时要小得多，特别是气阻3几乎无衰减作用(即气容2加气阻3与单独气容2的衰减作用相当)，这是因为压力波动经过气容后已经有很大的衰减，再经过气阻时，气阻内气速已很小，气阻是靠气体流动产生的流动阻力来产生作用的，当气速很小时，其作用就会大幅减小；从图3d可看出，气阻加气容的衰减作用也大于单独气容或单独气阻；同样地，经过气阻后，气容的衰减作用不会被弱化，这是因为气容的衰减作用不需要高气速，事实上气速越小气容衰减作用越强。总之，气容与气阻组合之后的衰减作用不是单独气容和单独气阻衰减作用的简单叠加。

表1 编号与实验条件的对应关系Table 1 Correspondence between serial number and experimental condition

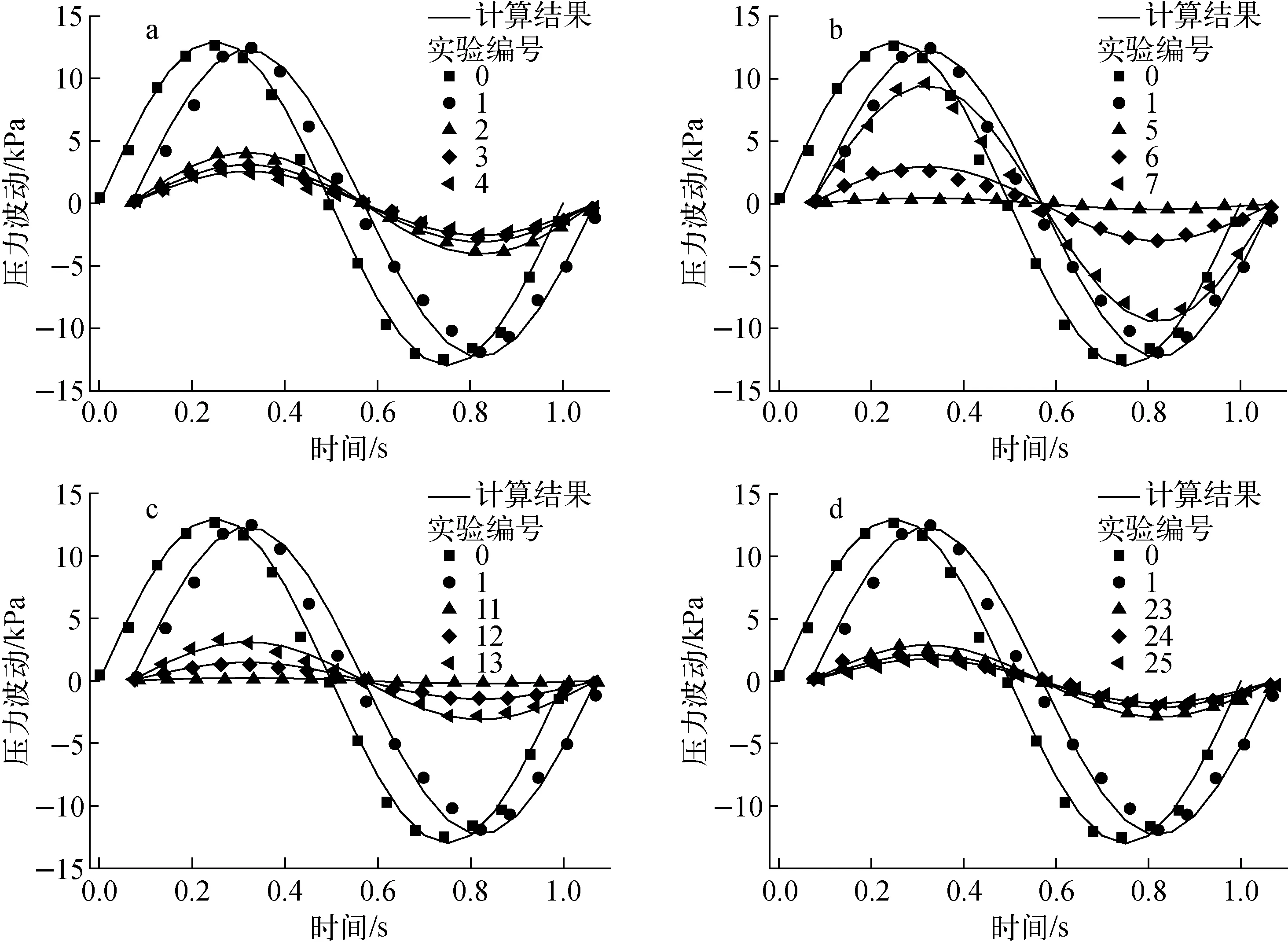
a——包含单独气容气路；b——包含单独气阻气路；c——先气容后气阻气路；d——先气阻后气容气路

3.2 气容和气阻对压力波动的影响

图3为瞬间压降时间序列信号的波动图。波动的幅值和相位是两个重要参数，从图3可看出，气容和气阻对压力信号的相位几乎无影响，因此本节主要研究气容和气阻对压力波动幅值的影响。在单气容和单气阻的情况下它们对压力波动幅值的影响示于图4。由图4可见，随着气容体积的增大，压力波动幅值减小，且气容的影响在其体积小时明显，随着气容体积的增大，其影响越来越小；随着气阻内径的减小，压力波动幅值减小，且随着气阻内径的增大，其影响越来越小。

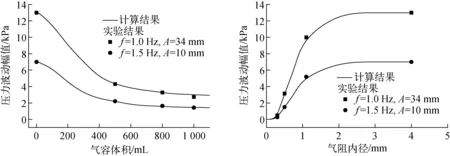
图4 气容和气阻对压力波动幅值的影响Fig.4 Effect of air capacity and air resistance on pressure amplitude

为更好地描述气容和气阻对压力波动的衰减作用，定义衰减后的压力波动幅值与衰减前的压力波动幅值之比为衰减系数K，衰减系数越小说明衰减作用越强，衰减系数越接近1，说明衰减作用越弱。经过对不同频率和振幅条件下的衰减系数的测量和计算发现，频率和振幅对其影响不大，基本取决于气容和气阻，因此可认为衰减系数是气容和气阻的本征属性。

图5示出了单气容和气阻及不同的气容和气阻组合的衰减系数的柱状图。由图5可见，衰减系数<5%的情况有：单独气阻1、气容1加气阻1、气容2加气阻1、气容3加气阻1、气阻1加气容1、气阻1加气容2、气阻1加气容3、气阻2加气容2、气阻2加气容3。可见，所有包含气阻1的组合均可使衰减系数低于5%，此外还有气阻2加气容2和气阻2加气容3这2种组合也能满足衰减系数<5%的要求。

图5 不同气容和气阻组合的衰减系数Fig.5 Attenuation coefficient of different air capacity and air resistance combinations

从图5还可看出，对于同样的气容和气阻，先气阻后气容的组合，其衰减作用要大于先气容后气阻的组合。为更准确地研究气容和气阻组合的衰减系数，将组合衰减系数与单气容和单气阻衰减系数的乘积进行对比，并进行线性拟合，结果示于图6。根据拟合结果，气容和气阻的组合衰减系数可用下式描述：

KC-R=1.35KCKR

(10)

KR-C=0.89KCKR

(11)

其中：KC-R为先气容后气阻的组合衰减系数；KR-C为先气阻后气容的组合衰减系数。可见，先气容后气阻的组合衰减系数较气容和气阻衰减系数的乘积大，而先气阻后气容组合的衰减系数较气容和气阻衰减系数的乘积小。这是因为气阻在高气速情况下更能发挥衰减作用，而气容则正好相反，先气阻后气容的组合方式综合利用了二者的优势。因此在实际应用中，推荐使用先气阻后气容的组合方式。

图6 衰减系数拟合Fig.6 Fitting of attenuation coefficient

3.3 气容和气阻对吹气管内气速分布的影响

通过方程及相应的定解条件的求解，还可得到气体在吹气管线任一位置x和任一时刻t的瞬间速度u，这是实验在不影响气路结构的情况下很难测定的参数，可为实验测量提供一个很好的补充。在脉冲频率为1 Hz、脉冲振幅为34 mm的条件下，对于无气容和气阻、含单独气容、含单独气阻3种不同情况，沿吹气管线5个不同位置的气体瞬间速度在1个周期内随时间的变化如图7所示。由图7可知：在x=0即吹气杯与吹气管道连接处，气体平均速度最大，随着与吹气杯距离的增大，气体平均速度逐渐减小，并且速度波动相对于x=0时延迟。对比图7a、b、c可知，气容和气阻的加入使吹气管出口处的流速略有减小，但影响不大。气容的加入对气速分布影响明显，吹气管内部，特别是后段(如x=13.6 m处)的流速受影响最明显。气容加入后吹气管后段的流速明显增大，且相位延后，这是因为气容加入后相当于在吹气管后端提供了一个接近开放的边界，不同于无气容时的封闭边界，吹气杯、吹气管和气容构成了一个振荡通路，使气速分布发生明显改变。而气阻的加入则对吹气管内气速分布影响很小，这是因为气阻所提供的边界条件很接近于无气容和气阻时的封闭边界。

a——气路无气容和气阻；b——气路含气容；c——气路含气阻

在前期研究[13]中曾提出，基于理论模型所计算的吹气管出口(x=0)处的气体瞬时流速u，通过对其正值半周期的积分，可计算出吹气管口在半个周期内气体进入的体积V，也就是在脉冲条件下液体压入吹气杯的体积，这对吹气杯的尺寸设计有重要参考意义。计算公式如下：

u>0,0

(12)

通过此公式计算得图7a中脉冲振幅值为34 mm时，液体压入吹气杯体积约为28 mL，而实验所采用的吹气杯体积为50 mL，即液体没有进入吹气管中。由于气容和气阻的加入对吹气管出口处的气速影响不大，所以气容和气阻的加入不影响吹气杯的设计。

4 结论

本文从理论和实验两方面对吹气法测量中气容和气阻的影响进行系统研究，得到如下结论：

1) 气容和气阻对压力波动信号有明显的衰减作用，随着气容体积的增大和气阻内径的减小，衰减作用增强；

2) 气容和气阻对压力波动信号的延迟作用可忽略；

3) 气容和气阻的组合衰减作用大于相应的单气容或单气阻的衰减作用；

4) 对于相同的气容和气阻，先气阻后气容的组合方式的衰减作用大于先气容后气阻的衰减作用；

5) 拟合得到了根据单气容和单气阻的衰减系数计算气容和气阻组合衰减系数的公式；

6) 气容和气阻的引入对吹气管出口处的气速影响不大，所以对吹气杯的设计无影响；

7) 气容的加入对吹气管内气速分布有明显影响，使吹气管后段气速明显增大，并发生相位延迟。

本文的理论与实验结果为吹气法的应用提供了依据，为气容和气阻的设计和应用提供了基础。

[1] 袁世颐. 乏燃料后处理中试厂间接式和非接触式测量仪表的研究及应用[J]. 核科技进展,2005(3):24-32.

[2] 陈靖,徐世平,吴秋林,等. 吹气法在线测量脉冲萃取柱参数研究[J]. 原子能科学技术,2001,35(增刊):34-40.

CHEN Jing, XU Shiping, WU Qiulin, et al. On-line measurement of pulsed column parameters by air purge[J]. Atomic Energy Science and Technology, 2001, 35 (Suppl.): 34-40(in Chinese).

[3] 王悦云,景山,吴伟,等.φ50 mm折流板脉冲萃取柱吹气法测量存留分数[J]. 化工学报,2005,56(7):1 253-1 259.

WANG Yueyun, JING Shan, WU Wei, et al. Determination of holdup by air purge inφ50 mm discs and doughnuts pulsed extraction column[J]. Journal of Chemical Industry and Engineering (China), 2005, 56(7): 1 253-1 259(in Chinese).

[4] 景山,吴秋林,王悦云,等. 吹气对喷嘴板脉冲萃取柱脉冲振幅测量的影响[J]. 原子能科学技术,2007,41(5):537-539.

JING Shan, WU Qiulin, WANG Yueyun, et al. Effect of air purge on the measurement of pulsed amplitude for pulsed extraction column[J]. Atomic Energy Science and Technology, 2007, 41(5): 537-539(in Chinese).

[5] 景山,王悦云,吴秋林. 吹气法在线测量折流板脉冲萃取柱脉冲操作参数[J]. 原子能科学技术,2007,41(6):716-721.

JING Shan, WANG Yueyun, WU Qiulin. On-line determination of pulsed parameters for pulsed extraction column with discs and doughnuts by air purge method[J]. Atomic Energy Science and Technology, 2007, 41(6): 716-721(in Chinese).

[6] 景山,吴秋林,王悦云. 标准喷嘴板脉冲萃取柱脉冲振幅的在线测量[J]. 原子能科学技术,2008,42(4):292-295.

JING Shan, WU Qiulin, WANG Yueyun. On-line measurement of pulsed amplitude for standard spray-sieve-plate pulsed extraction column[J]. Atomic Energy Science and Technology, 2008, 42(4): 292-295(in Chinese).

[7] 景山,吴秋林. 空气脉冲对吹气法测量萃取柱下澄清段压力的影响[J]. 原子能科学技术,2008,42(5):408-415.

JING Shan, WU Qiulin. Effect of air pulsation on the pressure measurement in bottom settler of pulsed extraction column by air purge method[J]. Atomic Energy Science and Technology, 2008, 42(5): 408-415(in Chinese).

[8] 景山,吴秋林. 脉冲萃取柱下澄清段的吹气法管道设计原则[J]. 原子能科学技术,2008,42(7):602-605.

JING Shan, WU Qiulin. Design method of air tube in bottom settler of pulsed extraction column for air purge method[J]. Atomic Energy Science and Technology, 2008, 42(7): 602-605(in Chinese).

[9] 宋子龙. 脉冲萃取柱有关参数稳定测量的研究[J]. 核科技进展,2005(3):35-46.

[10]宋子龙,赵晓兰,牛爱文,等. 脉冲萃取柱有关参数稳定测量的继续研究[J]. 核科技进展,2006(3):252-268.

[11]王健,张正斌,李靖,等. 中试工程脉冲萃取柱系统调试与改进[J]. 核科技进展,2006(3):225-243.

[12]刘宇. 吹气仪表在中试厂的应用[J]. 核科技进展,2005(3):47-57.

[13]李少伟,曾鑫,景山,等. 吹气管长度对脉冲萃取柱柱重瞬间压降信号测量的影响[J]. 原子能科学技术,2014,48(3):395-400.

LI Shaowei, ZENG Xin, JING Shan, et al. Effect of tube length on measurement of instantaneous pressure drop of column weight in pulsed extraction column[J]. Atomic Energy Science and Technology, 2014, 48(3): 395-400(in Chinese).

Effect of Air Capacity and Air Resistance on Measurement of Instantaneous Pressure Drop of Column Weight in Pulsed Extraction Column

ZENG Xin1, LI Shao-wei2, JING Shan2, LIU Ji-lian1, WU Qiu-lin2

(1.ElectricalInstrumentDepartment,ChinaNuclearPowerEngineeringCo.,Ltd.,Beijing100840,China; 2.InstituteofNuclearandNewEnergyTechnology,TsinghuaUniversity,Beijing100084,China)

The theoretical and experimental studies about the effect of air capacity and air resistance in the air purge method were carried out. The results show that the air capacity and air resistance have obvious attenuation effect on the pressure amplitude but little effect on the phase position of the pressure wave. The attenuation effect increases with the air capacity volume increasing or the air resistance diameter decreasing. The attenuation effect of the air capacity and air resistance combination is bigger than that of a single air capacity or a single air resistance. The combination attenuation effect is bigger when the air resistance is before the air capacity. The air capacity and air resistance have little effect on the air velocity at the entrance of the purge tube and thus have no effect on the design of the purge cup. The theoretical and experimental results in this article provide fundamental for the design and application of the air capacity and air resistance in the air purge method.

air purge method; air capacity; air resistance; instantaneous pressure drop of column weight; pulsed extraction column

2014-02-27;

2014-03-28

曾 鑫(1980—)，男，四川内江人，工程师，从事核化工自动化控制研究

TQ028.4

A

1000-6931(2015)06-0997-08

10.7538/yzk.2015.49.06.0997