非能动余热排出换热器换热能力数值分析

张文文，丛腾龙，田文喜，秋穗正，苏光辉，谢永诚，蒋 兴

（1.西安交通大学 能源与动力工程学院，陕西 西安 710049；2.上海核工程研究设计院，上海 200233）

AP1000核电厂采用非能动设计来提高核电厂安全性并简化核电厂设备。对于非丧失冷却剂事故（LOCA），非能动余热排出系统（PRHRS）起着至关重要的作用。PRHRS主要包括非能动余热排出换热器（PRHR－HX）与安全壳内置换料水箱（IRWST）。在正常运行阶段，PRHR－HX出口管线上的阀门处于关闭状态，当安注信号发出后，蒸汽发生器被隔离，PRHRS投入运行，一回路冷却剂通过自然循环的方式将热量带至PRHR－HX。IRWST为衰变热的热阱，与PRHR－HX间存在两种换热方式：自然对流换热与沸腾换热。在PRHRS运行初期，IRWST内冷却剂处于高度过冷状态，单相自然对流换热是其主要换热机制。

PRHR－HX传热管数目庞大，采用直接建模对计算能力要求极高，并不适合瞬态分析。目前，针对PRHRS的数值模拟主要是通过减少传热管数来进行模拟，如Strohecker［1］针对AP600试验台架APEX，选取4根传热管分别对单相对流与过冷沸腾阶段进行了研究；薛若军等［2］以 AP1000核电厂内 PRHR－HX 为研究对象，通过模型简化对其进行了非稳态特性的模拟。为了简化几何建模，多孔介质模型已成功应用到相同复杂结构的管壳式换热器中，Prithiviraj等［3－4］基于多孔介质模型研究了管壳式换热器的流动换热特性；Zhang等［5－6］对冷凝器内的冷凝现象进行了准三维模拟；Cong等［7］对蒸汽发生器二次侧三维两相流场进行了稳态分析。

基于上述工作，本文采用多孔介质模型对PRHR－HX进行全尺寸建模，并采用一回路侧与IRWST侧耦合换热的方法对其非稳态流动换热特性进行分析计算。

1 数学物理模型

1.1 耦合换热模型

传热管管壁两侧耦合换热计算可克服采用给定传热管外壁热边界计算方法的不足，使得计算更接近实际物理现象，可更准确地分析换热器的热量输出能力。

传热管束区的热流密度通过下式计算：

其中：Tp和Ts分别为一回路冷却剂温度与IRWST侧冷却剂温度；hp为传热管内壁换热系数；hs为传热管外壁换热系数；k为传热管热导率；do为传热管外径；di为传热管内径。

在多孔介质模型的应用过程中，换热量以体积热源的形式添加进能量方程中，对于管束区，体积热源计算公式如下：

其中，ASV为体积面积密度，即单位体积内的传热管的换热面积。

对于传热管管壁内侧强迫对流换热系数采用Dittus－Bolter公式：

分别对水平管束区与竖直管束区进行传热管管壁外侧换热系数的计算。对于水平管束区，管外单相自然对流使用了Langmuir关系式［8］，该关系式由无限空间内水平单管换热式发展而来，形式如下：

其中，瑞利数Ra计算过程中采用管外径作为特征长度。

对于竖直管束区管外单相自然对流，使用了 Churchill－Chu关系式［9］，形式如下：

其中，下部水平管束区的高度作为该式计算过程中的特征长度。该关系式适用于格拉晓夫数大于1010的工况，而所有的计算工况均符合该条件。

1.2 分布阻力模型

本文计算中考虑的阻力由管束造成，并作为分布阻力添加进相应区域的各单元内。管束区阻力的计算包括轴向流动阻力及横向流动阻力，又因C型管的阻力为各向异性，因此在3个方向上分别添加以各方向速度分量计算的分布阻力。轴向流动阻力由下式计算：

其中：G为质量流量；Δpa为轴向压降；l为轴向长度；ρ为冷却剂密度；de为流通通道当量直径；fa为轴向流动摩擦系数，由 MacAdams公式［10］计算：

横向流动阻力公式如下：

其中：Δpc为长度为l的横向流动压降；fc为横向流动摩擦系数；vmax为管束间最窄流通截面的流速；pv为棒距。

与轴向流动不同的是，采用棒距pv作为特征长度，特征速度采用管束间最窄流通截面的流速vmax，横向流动阻力系数采用Grimison经验关系式［11］：

1.3 Boussinesq假设

在计算过程中，IRWST被处理为封闭腔室，为满足连续性方程，冷却剂密度需假设为常数。因此，采用Boussinesq假设，在守恒方程求解过程中，密度为定值，而在求解动量方程时，浮力项所包含的密度变化与温度变化相关，即：

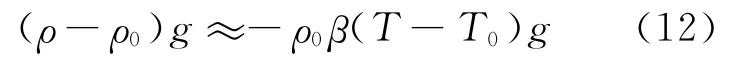
其中：ρ0为参考密度；T0为参考温度；β为体积膨胀系数；g为重力加速度。

1.4 湍流模型

PRHR－HX／IRWST系统瞬态计算时间跨度较大，考虑到计算能力限制，在建模时采用粗网格处理方法，因此采用对网格要求不高的Spalart－Allmaras模型，该模型属于以Boussinesq假设为前提的涡粘性模型，通过求解中间变量的输运方程获得湍流运动的黏性系数［12］：

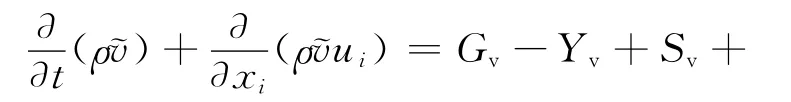
1.5 数值计算流程

采用商用CFD软件FLUENT对模型进行求解。为了得到实时的换热量，分别准确计算出传热管管壁两侧流场及温度场以获得其换热系数，在每步迭代后进行换热量计算。图1示出PRHR－HX数值计算的流程。

图1 PRHR－HX数值计算流程Fig.1 Calculation procedure of PRHR－HX

2 几何模型与边界条件

IRWST内包括1个PRHR－HX与2个ADS泄压喷淋器。本文着重分析传热管束区及周边的流动换热特性，不考虑在事故后期阶段才投入使用的泄压喷淋器。PRHR／IRWST系统结构如图2所示，忽略支撑板与外壳框架，IRWST为半铜钱结构，传热管束区采用多孔介质模型处理，只对外部轮廓进行建模。一回路冷却剂由上部入口封头进入，经水平管束区热段、竖直管束区以及水平管束区冷段后，由出口封头流出。

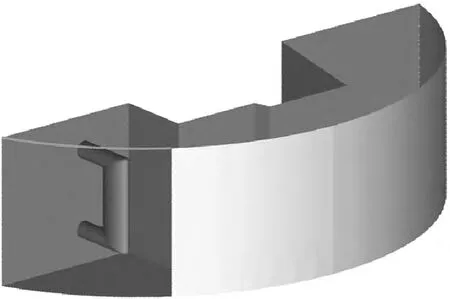
图2 计算区域结构Fig.2 Structure of calculated domain

AP1000PRHR－HX共有689根传热管，分为29排29列，水平管束区纵横棒距相同，而竖直管束区纵横棒距相差一倍，其详细结构如图3所示。为了进行耦合换热计算，将传热管束区沿一回路冷却剂流动方向划分为20个控制体，如图4所示，并假设每个控制体内一回路侧网格内参数相同。

图3 非能动余热排出换热器结构Fig.3 Structure of PRHR－HX

一回路侧冷却剂入口温度与流量采用RELAP5对AP1000核电厂全厂断电事故的分析结果，同时忽略一回路压力降低对冷却剂物性的影响。为了避免对水箱上部气液交界面进行建模，将IRWST顶部自由液面处理为零切应力绝热壁面，忽略上表面热量散失。计算中，IRWST内冷却剂的初始温度设为322K。

图4 一回路侧控制体划分Fig.4 Division of control volume in primary loop side

3 结果分析

3.1 IRWST侧流动换热计算结果

伴随着热量导入IRWST内，冷却剂受热膨胀，在浮力的驱动下，热流体向上流动，在壁面附近方向发生偏转。图5示出500s与3000s时IRWST内的流线分布。由图5可见：500s时自然循环尚处于启动阶段，流体上升到上部区域后转向向IRWST远端流动，到达远端后从水箱下部返回到传热管束下部，形成竖直方向内的自然循环；3000s时，流动已经基本稳定，此时，在水箱上部形成水平涡，即流动集中在上部，而竖直方向上的循环变得较弱。

图5 IRWST内的流线图Fig.5 Stream line in IRWST

图6示出不同时刻对称面处的速度矢量分布。由图6可看出，在500s时大流速区主要集中在竖直传热管束附近，而在3000s时上部水平管束区上方速度较大。这是由于在启动阶段，管束区内、外温差较大，驱动较强，同时竖直管束区通道阻力较小，流道长，因此速度较大，可达2m／s左右。随着循环建立，上部区域形成水平涡，折返的流体与水平管上升流体汇聚，故此处速度较大。同时可见，IRWST非管束主体区域的冷却剂流动性较差，下壁面附近冷却剂近似停滞。

图7示出不同时刻IRWST内冷却剂的温度分布剖面图，计算结果非常直观地表现了热分层现象的形成及发展。热分层现象的形成主要与两个因素有关，热流体在上部区域的积聚与IRWST内主体区域冷却剂较小的流动性。前者使得热边界层在箱内上部区域形成并逐渐向底部区域发展，后者则降低了各温度层间的相互搅混，使得热分层较为稳定。同时，从图7中还可看出，最高温度出现于上部水平管束区，而箱体底部的“死水区”的温度则基本维持在初始温度水平。

图6 IRWST对称面处的速度矢量分布Fig.6 Velocity vector distribution on symmetry plane in IRWST

图7 不同时刻IRWST内冷却剂温度分布Fig.7 Coolant temperature distribution of IRWST at different time

3.2 耦合换热计算结果

图8、9分别示出传热管内壁及外壁对流换热系数的分布。因管内冷却剂温度沿一回路流动方向逐渐降低，造成冷却剂密度增大而黏性减小，导致管内换热系数逐渐降低。冷却剂温度随时间的增加而降低，同样导致换热系数降低。由图8可见，管内壁换热系数基本处于9～15kW／（m2·K）范围内，变化相对较小。

图8 一回路侧沿冷却剂流动方向的换热系数Fig.8 Heat transfer coefficient of primary loop side along flow direction of primary fluid

对于管外对流换热，与管内对流换热相比影响因素较多，管束的排列方式及流动方向均对其产生影响。由图9可看出，管外壁换热系数较小且分布较不均匀，最大值为2.5kW／（m2·K），最小值仅为1kW／（m2·K）左右。竖直管束区的换热系数最大，尽管该区域的冷却剂流动方式为换热性较差的平行于管束流动，因该区域长通道及低阻力的特点，使得其速度远大于水平管束区，进而换热系数也高于横掠管束流动的水平管束区。

图9 IRWST侧沿一回路冷却剂流动方向的换热系数Fig.9 Heat transfer coefficient of IRWST side along flow direction of primary fluid

图10示出一回路侧冷却剂不同时刻的温度分布。由图10可见，一回路侧入出口温降由500s时的130K减小至5000s时110K。水平管束区热段及竖直管束区上半部各部分温度随时间的增加而降低，而竖直管束下半部与水平管束区冷段温度随时间的增加反而升高。产生这种现象的原因主要是由于上游换热能力的降低使得一回路侧冷却剂的沿程温降减小所致。

图10 一回路侧沿冷却剂流动方向的平均温度分布Fig.10 Average temperature distribution of primary loop side along flow direction of primary fluid

图11示出管束区域不同时刻的能量源项分布。换热量的大小主要与两侧流体温差及热阻相关，其中，分布极不均匀的管壁外侧换热系数是传热过程的主要热阻。但因竖直管束区的传热管排列稀疏，单位体积有效换热面积较小，故其能量源项分布与图9所示的换热系数分布并不相同。

图11 一回路侧沿冷却剂流动方向的能量源项分布Fig.11 Energy source distribution of primary loop side along flow direction of primary fluid

对各部分换热量求和即得到换热器总换热量随时间的变化趋势，如图12所示。在前5000s内，PRHR－HX的热负荷由150MW 下降至约80MW。一回路侧入口温度及流量降低，IRWST内冷却剂温度升高，使得两侧温差减小，导致换热器换热能力下降。

图12 换热器总换热量随时间的变化Fig.12 Total heat transfer of heat exchanger vs time

4 结语

本文采用多孔介质模型，对AP1000核电厂PRHR－HX进行了数值模拟，得出如下结论。

1）采用多孔介质模型模拟PRHR－HX，相比采用常规CFD网格的方法，大幅节省了几何建模时间与计算量，同时可获得精度较高的计算结果；

2）系统投入运行后，IRWST内冷却剂的流动主要发生在传热管束区及箱体上部区域，同时热流体在上部区域的聚集造成了明显的热分层现象；

3）传热管管壁外侧换热系数要小于一回路侧，是换热器工作的主要热阻，且分布较不均匀，换热量计算的正确与否取决于该换热系数计算的准确性；

4）随着时间的增加，一回路自然循环能力的降低导致入口流量的下降，以及换料水箱内冷却剂温度升高使得传热管两侧温差降低，其自然对流强度下降，造成换热器总换热量逐渐减小。

［1]STROHECKER M F.Investigation of the IRWST flow patterns during a simulated station blackout experiment on the OSU APEX facility［D］.USA：Oregon State University，1998.

［2]薛若军，邓程程，彭敏俊.非能动余热排出热交换器数值模拟［J］.原子能科学技术，2010，44（4）：429－435.XUE Ruojun，DENG Chengcheng，PENG Minjun.Numerical simulation of passive residual heat removal heat exchanger［J］.Atomic EnergyScience and Technology，2010，44（4）：429－435（in Chinese）.

［3]PRITHIVIRAJ M，ANDREWS M.Three dimensional numerical simulation of shell－and－tube heat exchangers，Ⅰ：Foundation and fluid mechanics［J］.Numer Heat Transfer：Part A Appl，1998，33（8）：799－816.

［4]PRITHIVIRAJ M， ANDREWS M. Threedimensional numerical simulation of shell－andtube heat exchangers，Ⅱ：Heat transfer［J］.Numer Heat Transfer：Part A Appl，1998，33（8）：817－828.

［5]ZHANG C，BOKIL A.A quasi－three－dimensional approach to simulate the two－phase fluid flow and heat transfer in condensers［J］.International Journal of Heat and Mass Transfer，1997，40（10）：3537－3546.

［6]ZHANG C.Numerical modeling using aquasithree－dimensional procedure for large power plant condensers［J］.Journal of Heat Transfer，1994，116（1）：180－188.

［7]CONG Tenglong，TIAN Wenxi，SU Guanghui，et al.Three－dimensional study on steady thermohydraulics characteristics in secondary side of steam generator［J］.Progress in Nuclear Energy，2014，70（1）：188－198.

［8]YONOMOTO T，KUKITA Y，SCHULTZ R R.Heat transfer analysis of the passive residual heat removal system in ROSA／AP600experiments［J］.Nuclear Technology，1998，124（1）：18－30.

［9]CHURCHILL S W，CHU H S.Correlating equations for laminar and turbulent free convection from a vertical plate［J］.International Journal of Heat and Mass Transfer，1975，18（11）：1323－1329.

［10］MacADAMS W H.Heat transmission［M］.New York，US：McGraw Hill，1954.

［11］GRIMISON E.Correlation and utilization of new data on flow resistance and heat transfer for cross flow of gases over tube banks［J］.Trans ASME，1937，59：583－594.

［12］SPALART P，ALLMARAS S.A one－equation turbulence model for aerodynamic flows，Technical report AIAA－92－0439［R］.US：American Institute of Aeronautics and Astronautics，1992.