标准能量冲击下桥梁动态响应仿真分析

许可时

(中国中铁航空港集团北京机场工程分公司，北京海淀区 100097)



标准能量冲击下桥梁动态响应仿真分析

许可时

(中国中铁航空港集团北京机场工程分公司，北京海淀区 100097)

基于在桥梁动载试验中,截面最大动位移响应受到桥面不平整度的影响难以取值,讨论标定能量冲击荷载得到某一截面的最大动位移的可行性。通过ANSYS/LS-DYNA动力分析方法,计入行车阶段车桥耦合振动,模拟桥梁跨中截面在不同平整度的情况下,车辆行驶至跨中并进行标定枕木高度的跳车试验下的竖向位移时间历程响应。排除动载试验中桥面不平整度的影响。

桥面不平整度;能量冲击;冲击系数;动位移;桥梁力学性能

1 引言

近年来，为满足不断增加的交通量，交通工程迅速发展。桥梁作为交通体系中的不可或缺的组成部分，呈现出大跨度和结构形式多样化的发展趋势。同时，桥梁的超期服役和破损十分严重。如何在不影响交通通行的情况下快速准确检测桥梁健康状况是工程上急需解决的问题。

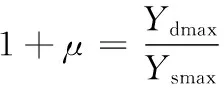
本文通过桥面法向的标准能量冲击试验，获得桥梁的竖向动位移响应。试验方法为，车辆行驶至指定位置进行标定枕木高度的跳车试验。由于标定高度远大于不平整桥面上的最大凹凸值，由此产生的能量激励一定大于不平整度引起的车桥耦合振动位移峰值，在此基础上对桥梁的动位移响应进行测试，得到桥梁的最大动位移。通过标准化的测试方法排除在动载试验中，桥面不平整度的影响。本文将对比不同平整度下桥面跑车和桥面跳车两种加载模式下桥梁的动位移响应，来分析通过标准能量冲击测量桥梁动位移的可行性。

2 标准能量测试跳车高度实验室预估

在标准能量冲击中，冲击能量的大小由执行冲击的车辆荷载及跳车高度决定，因此选取合适的车辆荷载和跳车高度很重要。在跳车试验中，跳车高度越高冲击能量越大，由此产生的激励作用越明显，获取的桥梁动力响应中信噪比也越高。但是过大的跳车高度实施困难，且对桥梁结构本身有破坏作用。桥梁对于静载的竖向位移响应与桥梁的EI值有关，且竖向响应随静载线性变化。模拟相同挠度下的小型跳车试验，探讨合适的跳车高度。

2.1 实验室试件及试验工况

为了在试验中获得比较清晰的响应，试验试件采用柔性较大的结构试件尺寸4000mm×500mm×100mm，C30混凝土，配筋6φ12，箍筋和架力筋采用构造配筋。支撑形式为简支。

2.2 实验室动载测试

在环境激励下测得试件的基频为7.44Hz。 跨中截面在45kg静载下竖向位移为1.4mm，挠度为0.0007采用轮距为400mm的小车在试件上进行加载。由于试件尺寸与实际桥梁差距太大，只用来对跳车高度进行估计。采用试件桥梁与实际桥梁相同静载挠度下的加载重量作为跳车的加载重量。跳车高度分别选取梁长的1/400，1/300，1/200，即1cm，1.3cm，2cm进行跳车试验。测得试件的竖向位移响应如下：

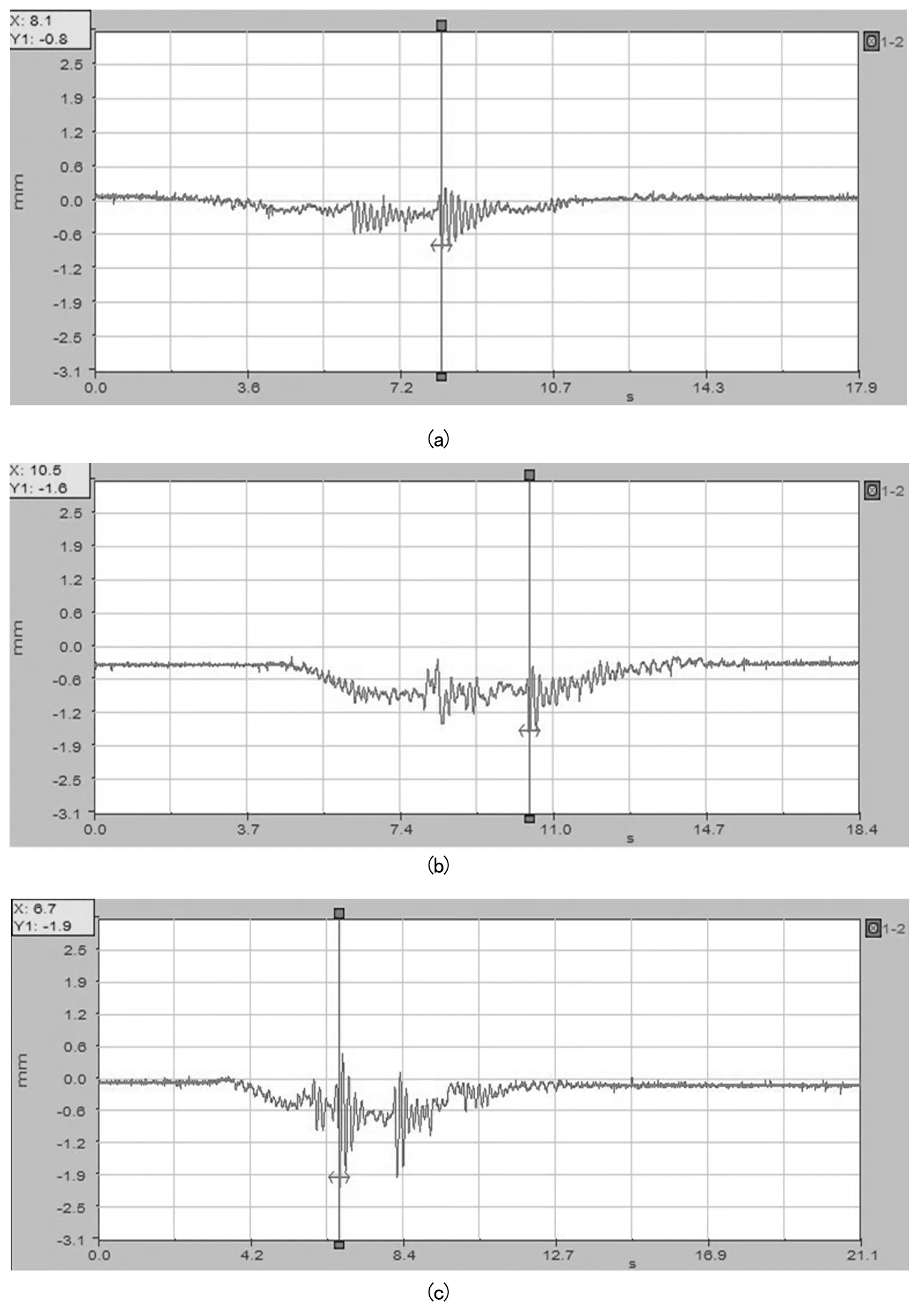
图2.1

图中最大值出现时间不同是由于信号采集开始后人为准备时间不同造成的，在2.1(c)中最大值出现在前轮着地时，是加载物移动造成的。如图所示：1cm，1.3cm，2cm高度跳车下竖向位移分别为1.5mm，1.6mm，1.9mm，理论动载竖向位移响应为1.87mm，因此选用跳车高度为梁长的1/200。

3 算例

在移动荷载的影响下，桥梁结构受迫振动。车辆由于自身减震系统引起的扰动频率不能忽视，构成车桥耦合振动系统。在此系统中，由于假定在移动过程中车轮始终与桥面接触，桥面不平整度引起车辆对桥梁冲击荷载的变化十分显著。

3.1 车辆模型建立

选用四分之一车辆模型，只考虑车辆对于桥面的垂直向冲击，将车身是为具有一定质量的均质刚体。通过弹簧和阻尼器模拟轮胎的刚度和阻尼。轮胎是悬挂质量。并假设左右车辙的不平整度函数相等，前后轴的垂直方向的运动相互独立不产生耦合，这时可以把车辆模型简化为四分之一模型进行分析。车辆具有两个自由度，假设车身是刚体，只考虑车辆在竖直方向上的振动，车轮在行驶过程中(不包含跳车过程中的荷载步)始终与地面相接触。

3.2 桥面不平整度模型的建立

根据国际标准化协会(ISO)给出的功率谱道路平整度分级方法计算道路不平整度r(x)，而且认为功率谱密度是具有零均值的平稳过程。考虑汽车隔振作用的功率谱密度表达式为：

(式3.1)

其中ku、kl为需要的路面空间频率的上、下限，不同等级路面数值按照下表选取：

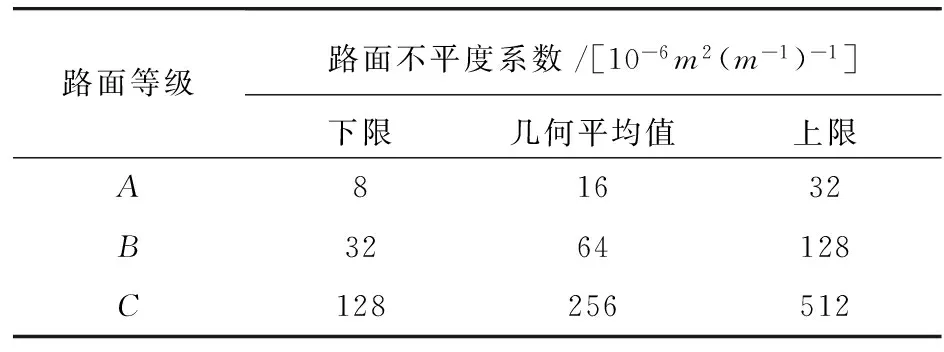
表3.1

根据三角级数法建立路面不平整度模型，路面不平整度样本波形按式3.1计算

(式3.2)

根据车辆桥梁位移几何相容性：

zw=u(x)+r(x)

(式3.3)

车辆与桥梁的力学平衡条件：

(式3.4)

基于上述假设得到考虑耦合振动和桥面不平整度的车辆对桥梁的总荷载：

(式3.5)

3.3 考虑桥面不平整度的桥梁跨中截面跳车模型建立

根据实验室的跳车高度预估，选取算例桥梁的跳车高度。在现行的桥梁设计与检测规范中没有关系跳车高度的统一规定。《交通部行业标准-大跨径混凝土桥梁的检验方法》中规定的跳车高度小于10cm，《交通部公路科学研究所-公路桥梁承载能力检测评定规程》中跳车高度小于15cm，本文设定跳车高度不大于15cm，对于不损伤桥梁的极限跳车高度在此不做讨论。

算例利用ANSYS/LS-DYNA动力显式求解系统，将车辆在跑车阶段对桥梁的激励情况以及由此产生的桥梁振动变形通过写入结果文件的形式在显式分析中以初始条件加载。由于选取四分之一车辆模型，车辆前后轮的分别激励不存在，在此条件下，设定车辆模型水平向的速度为跳车初始条件。

在动力显式模型分析中，基本思想是将整个结构离散化成有限单元，单元内部节点坐标插值得到，结构总势能的变分近似的表示为个单元势能变分之和。根据虚位移原理：

(式3.6)

在LS-DYNA中，一致单元质量矩阵me=∫VeρNTNdV同一行的元素都合并到对角元上形成集中质量阵，再集成整体对角质量矩阵M,则上式可改写为：

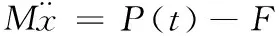
(式3.7)

其中F为单元应力场的等效节点力矢量组集而成，P为总体节点荷载向量，由集中节点力、面力、体力等形成。以此分析在任一时间点结构中各个节点的响应。

车轮与桥面接触算法采用对称罚函数算法，每一时步首先检查从节点十分穿透主表面，没有穿透则对该节点不做任何处理。如果穿透，则从该节点和被穿透主表面之间引入一个较大的界面接触力，其大小与穿透深度和主界面材料刚度成正比，即为罚函数值。

4 桥梁跨中跳车动力响应

基于有限元程序ANSYS，建立桥梁模型。据《公路桥涵设计通用设计规范》，冲击系数(1+μ)中μ的计算公式为：

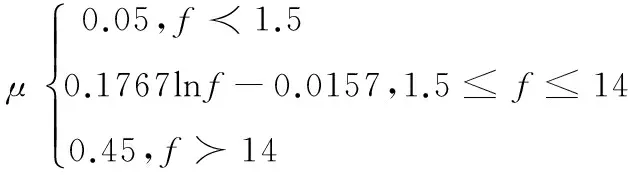
(式4.1)

桥梁模型采用等截面钢筋混凝土简支T梁，横向5片梁组成，梁长20.5米，计算跨度20米。梁高1.3米，翼缘宽度1.4米，腹板厚度0.2米。通过ANSYS计算得到该桥的一阶频率为5.573Hz。则由式4.1计算得到桥梁的冲击系数应为1.288。

4.1 桥梁跨中截面在不同桥面平整度跑车条件下的动力响应

车辆悬挂部分质量为ms=8900kg，非悬挂部分质量为mt=1000kg，悬挂刚度系数ks=2000KN/m，轮胎刚度系数为

kt=3500KN/m，悬挂系缓冲阻尼系数cs=30KNs/m，轮胎阻尼系数ct=4KNs/m，轮胎质量mw=100kg，车静重100000N。车辆在跨中位置静止是，跨中截面竖向位移为0.87cm。挠度0.0007，如图所示：

图4.1

车辆以10km/h的速度分别通过A、B、C级路面桥梁。模型在第21荷载步第二子步(沿梁纵向分为40个单元，每个荷载步有两个子步组成)作用下，即车辆行驶到桥梁跨中截面时， 不同平整度下桥梁跨中截面竖向位移的时间历程响应如下图：

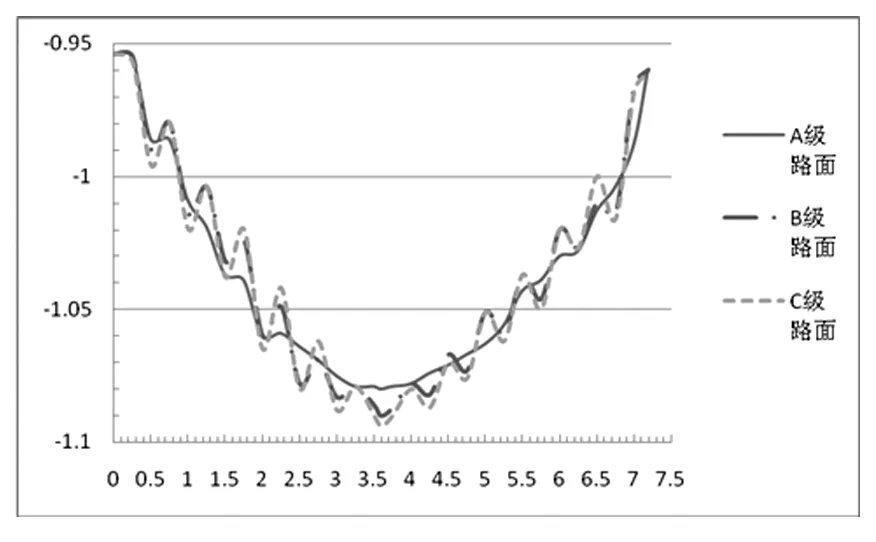
图4.2

如图例所示三条曲线分别表示重10t的车辆以10km/h的速度通过路面等级为A、B、C的桥面时，桥梁跨中截面在竖直方向上的位移。如图可知，随着桥面不平整度的增加，车辆对于桥梁结构的冲击荷载越来越明显。桥梁跨中截面竖向位移的时间历程响应呈现波动趋势，在同一时间点上桥梁跨中截面的竖向位移随桥面不平整度发生变化。两相邻时间点的跨中截面竖向位移差随桥梁不平整度的增加而增大。同时，车辆通过不同等级路面是桥梁跨中的最大位移值如下表4.1。

表4.1

由上表可知，车辆在不同平整度下对桥梁的冲击荷载随桥面不平整度的增加而增大。其中A级与C级路面的桥梁动位移响应差达到了0.14mm，若在模拟计算中假设桥面平整，则误差大于12.9%。且冲击系数也随之增大，且均小于规范中的计算值。说明桥梁结构冲击系数与冲击能量的大小有直接关系。

4.2 桥梁跨中截面跳车的动力响应

跨中截面，枕木高度为10cm时，跨中截面的竖向位移响应如图：

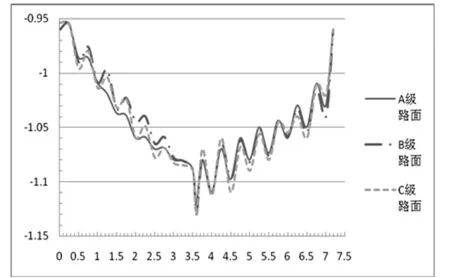
图4.3

如图所示三条曲线分别为A、B、C级路面上，车辆行驶至桥梁跨中位置跳车时，跨中截面竖向位移的时间历程响应曲线。由图可知，在车辆上桥至行驶到跨中阶段，桥梁跨中截面的竖向位移随桥面不平整度发生变化。且数值不稳定性随不平整度的增加而增大。跨中截面的竖向最大位移如表4.2。

表4.2

可知，跨中截面在跨中跳车的过程中，跨中截面的竖向最大位移产生在跨中跳车的时间点，且不同平整度下跳车激励的跨中截面竖向位移基本相同，即可知在标准能量冲击下最大动位移对桥面不平整度的响应不敏感，A级与C级路面的最大动位移值仅相差0.02mm。且在跳车发生后，桥梁的竖向位移时间历程响应比前段波动明显，由于桥梁自身的阻尼作用，随时间趋于平缓。

5 结论及建议

(1)本文通过实验室试件设定跳车高度，由于桥梁EI值受到桥梁长度、截面形式、支撑条件等多方面的影响，所以能量标准化冲击的跳车高度还需进一步探讨。

(2)进一步验证了在桥面跑车试验中，桥面不平整度对于桥梁的动态响应有很大的影响。

(3)通过ANSYS/LS-DYNA模拟的桥梁跨中跳车试验中，跨中截面的最大竖向位移值基本稳定，说明在跳车试验中冲击能量的扩大使得信噪比有很大的提高，跳车最大动位移对桥面不平整度不敏感。

(4)在标定高度10cm的跳车模拟中，跨中的最大动位移与根据静位移和冲击系数得到的理论值十分接近，说明通过该方法反算静位移，评定桥梁安全性是可行的。

(5)本文对于不同截面形式、长度、支撑条件下的桥梁适用的跳车高度没有进行系统分析，并且桥梁在结构出现损坏的情况下其动力响应是否依然符合此规律仍需验证。希望能进行进一步研究探讨。

Analysis of Dynamic Displacement Response of Bridge with Impact of Standard Energy

XU Ke-shi

(China Railway Airport Construction Group Co.Ltd Beijing Airport Engineering Branch)

Since it is too difficult to ensure impact coefficient under the influence of roughness of the bridge deck，we calculate displacement by standard energy. This paper simulates the bumping testing on the cross section of mid span by explicit dynamic FEM. A vehicle passes through the cross tie which is higher than the highest unevenness, and then gives an impact load to the cross section of the mid span for getting the maximum dynamic displacement of the cross section. This method can eliminate the influence of roughness of the bridge deck and it is a new pathway of bridge dynamic testing.

roughness of the bridge deck; impact of the standard energy; coefficient of the impact; dynamic displacement; bridge mechanical properties

2015-01-05

许可时(1985-)，女，河北张家口人，助理工程师，硕士，先后就读于河北工业大学土木工程学院、中国民航大学机场学院，现就职于中国中铁航空港集团北京机场工程分公司。研究方向：桥梁动力仿真分析及桥梁动态测试。

U446

A

1008-8156(2015)01-0054-05

修回日期：2015-02-25