自然灾害动态风险分析的一个形式化模型*
黄崇福
(1.地表过程与资源生态国家重点实验室(北京师范大学),北京100875;2.北京师范大学环境演变与自然灾害教育部重点实验室,北京100875;3.民政部/教育部减灾与应急管理研究院,北京100875)
自然灾害动态风险分析的一个形式化模型*
黄崇福1,2,3
(1.地表过程与资源生态国家重点实验室(北京师范大学),北京100875;2.北京师范大学环境演变与自然灾害教育部重点实验室,北京100875;3.民政部/教育部减灾与应急管理研究院,北京100875)
根据自然灾害动态风险分析基本原理,将概率风险模型改造成一个动态风险分析的形式化模型。由条件概率密度函数和动态脆弱性函数耦合而成的风险,随着综合环境和内在属性的变化而变化。我们建议用正态信息扩散方法估计条件概率密度函数和动态脆弱性函数。这两个重要函数的估计都不依赖人为假设,分析过程透明,结果可解释性强,具有一定的可靠性。
动态风险;自然灾害;密度函数;脆弱性函数;信息扩散
风险是一个幽灵,一个飘忽不定的幽灵。一旦显现,就不再是风险,而是事件。为了管理这个幽灵,使其不对人类造成过大的伤害,人类的一切智慧和可用的工具都被调动了起来,力图监测它、描述它、评估它,规避它,并在可能的情况下控制它。人们投巨资建造各种监测系统获取数据,提出越来越复杂的非线性模型,并使用大量数据以描述和评估风险,有实验得来的模型,有经验得来的模型,也有逻辑推理来的模型,还有从仿生学借鉴来的模型。新出现的或人们缺乏先验知识的风险,称之为“新兴风险”,例如,由于人类行为而放大了的自然风险[1];由大量统计数据支持概率模型而进行描述的风险,称之为“概率风险”[2],例如,一个地区的机动车事故风险;没有悬念,可以准确预测的“风险”,是“伪风险”[2],例如,可以准确预测:不带降落伞从高空飞机中跌落下来的人,必死无疑。
从“新兴风险”演变为“伪风险”,是人类对世界从未知到已知的一个认识过程,充满挑战。只有从静态风险分析上升到动态风险分析,才能加速这种演变。以2015年1月7日法国讽刺杂志《查理周刊》在首都巴黎的办公室遭到3名枪手袭击,造成12人死亡的恐怖袭击风险为例。事前,使用诸如统计假设等在内的任何静态模型,即便有再多的历史恐怖袭击事件的数据支撑模型,都描述不了这一风险。只有根据实时变化的恐怖分子活动的情报,以及作为风险承受体的该杂志办公室的现实设防情况等进行动态风险分析,才有意义。
在自然灾害领域,传统上,人们用大量历史数据进行概率风险计算,其有效性建立在平稳马尔可夫随机过程[3]的假定之上:风险系统是一个平稳马尔科夫过程,即未来的风险情景只与过去时间段内的情景有关,其相应的统计规律不因时间的推进而改变。这是一种静态风险评估方法,本质上假定了系统的随机规律不随时间发生变化。事实上,即使在统计的意义上,大多数风险系统也并非一成不变。六十多年前,黄河中下游地区洪水灾害风险极高,今天则已大大降低,这就是最好的例证。在社会快速发展和精细化管理的今天,粗糙的静态风险分析,已经满足不了需要。特别是,当灾害风险研究已经精细化到社区级时,风险的动态性,更是不可忽略。难怪龙卷风频发的美国,竟然被认为龙卷风的观测资料不足,难以确定各管理网格上龙卷风发生频率和强度的变化趋势[4]。
动态风险的研究,于20世纪80年代被提上了议事日程。目前,诸如故障树分析和事件树分析结合的蝴蝶结分析技术[5]、内集-外集模型[6]、风险评估框架修改[7]等更新算法,是动态风险分析的主要技术。回溯历史风险的动态过程的发展趋势预测方法,被用于研究洪涝灾害动态风险[8]。根据社会、政治、经济、金融、监管、法律和技术等因素对风险进行动态识别、定位和评估的“欧洲新兴风险雷达”[9],也是动态风险研究的重要尝试。
然而,更新算法和趋势预测法只适于研究惯性型动态风险,现有的风险雷达只是传统风险矩阵的一种雷达化显示,捕获和处理动态风险信息的问题并没有解决。
动态风险的研究进展缓慢,一个重要的原因是没有涉及动态风险的本质:内涵和外延都发生变化。另一个原因是人们过于热衷于非技术性概念化研究,陷入关于动态风险的性质[10]、准则[11]和时间序列[12]等方面的讨论。文献[13]中认为,面对一个给定的风险系统,当人们努力认识风险时,并不知真实风险为何物,因为真实风险将在一定时段后才能得到确认。据此,该文认为,研究动态风险只能在“认知动态风险”的概念下进行,并给出如下定义:
定义1 设不利事件ω的风险系统G随着综合环境E和内在属性C的变化而变化。假定其变化是通过对风险源S和风险承受体O的影响而实现。设“⊗”是我们通过耦合S和O而认识风险的某一数学算子,我们称Rω(E,C)=SE,C⊗OE,C为认知动态风险。
例如,1998年长江发生特大洪水后,我国政府投入巨资加固了长江堤防并在上游大面积退耕还林,不利事件ω(水灾)的风险系统G(天气系统和长江流域社会经济系统)的综合环境E(水土保持)和内在属性C(堤防)均发生了很大的改变,风险源S(洪水)发生了变化,从而长江流域的洪水灾害风险也必将发生变化,由Rω(水土保持,堤防)表达的风险,是一种认知动态风险。如果考虑全球气候变暖和社会经济系统的变化,风险的动态性会更明显。
面对如此界定的动态风险,该文提出了对其进行分析的基本原理:明确动态风险内涵和涉及的系统,研究综合环境和内在属性变化对风险源和风险承受体的影响,通过对变化中的风险源和风险承受体进行耦合,进行不确定性意义下的动态系统量化分析。
这里的“动态风险内涵”是指具体的动态风险定义,既要明确风险是指什么,更要明确动态是因什么而动,并以描述动态风险情景某一个或几个具体侧面的相关量化指标来体现。例如,如果风险是指损失的期望值,动态是因时间而动,则风险源强弱、风险承受体脆弱性、综合环境参数、内在属性参数、“损失”和“期望值有效时间长”等等,都是描述动态风险情景的量化指标。这里,不同时段期望值是描述动态损失风险情景的一个侧面。
这一基本原理的核心是“研究综合环境和内在属性变化对风险源和风险承受体的影响”,局限于能用“风险源和风险承受体耦合”生成的认知动态风险。本文将这一原理应用于自然灾害风险,构造出一个形式化模型,旨在为关心动态风险研究的学者起到抛砖引玉的作用。
1 动态概率风险的形式化模型
当人们用模型进行风险分析时,往往因研究的问题层次不同,采用不同层次的风险模型。这些模型,可分为三个层次,分别称为“概念化模型”、“形式化模型”和“应用模型”。
人们对风险的初级认识,使用概念化模型来进行分析。这种模型,只能指明影响风险的各种因素的名称。支撑模型的是这些因素后面的概念。例如,式(1)就是一个概念化模型。
R=F(H,V),
(1)
式中:R为风险,H为危险性,V为脆弱性。
当人们对风险有了一定的认识后,通常能提出形式化模型对风险进行分析。这种模型,能给出形式化的数学表述式,但函数的具体形式或全局性参数尚待确定。例如,式(2)就是一个形式化模型。

(2)
式中:R为风险,f(x)为危险事件x发生导致的损失程度,p(x)为危险事件x发生的概率密度函数。
只有当人们对风险有了较深刻的认识后,才有可能建立起实实在在对风险进行量化分析的应用模型。这种模型,给定了函数的具体形式和全局性参数。例如,估计水稻洪水风险的公式(3)[14],就是一个应用模型。
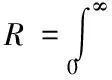
(3)
式中:R为风险,a为用损失数据进行统计,b为用洪水事件数据进行统计。a,b均是局部参数,由所评估地区的相关数据确定。
“概念化模型”通常用于定性研究风险问题;“形式化模型”是从定性研究到定量研究的阶段性成果。“应用模型”才可用于定量研究风险问题。
在人们认识静态风险的时代,评估风险的高或低,类似于我们评估某产品的质量好或不好;分析风险的高或低,则类似于我们分析某产品的质量为什么好或为什么不好。评估偏重于结果,分析偏重于原因、过程。评估可以通过观察外表或对有关参数进行测试来完成,也可通过分析有关原因、过程,推导出结果。简单的概率统计属于观察外表的方法,系统分析方法属于推导方法。采用何种方法,完全由我们进行风险评估时所拥有的数据资料和掌握的相关知识来决定。
在人们认识动态风险的时代,风险评估将被淡化,因为仅仅通过观察外表或对有关参数进行测试很难认识动态风险,只有通过分析有关原因、过程,才能推导出结果。根据动态风险分析的基本原理,形式化模型应该涉及四个方面的变量,分别用于刻画风险源、风险承受体、综合环境和内在属性。并且,形式化模型中,须用数学公式表述风险源和风险承受体是如何进行耦合的。无论是变量或耦合,均须考虑风险系统的不确定性。
下面,我们将引言中提到的动态风险分析基本原理应用于自然灾害风险,构造出一个动态概率风险的形式化模型。
人们对风险的认识程度完全受其掌握的知识和信息所决定。根据认知程度不同,风险可分为四类:伪风险、概率风险、模糊风险和不确定风险[2]。在一些地区,自然灾害频繁发生,在较大的地理单元上,自然灾害风险是概率风险。例如,人们可以用概率模型和大量数据来分别预测福建、浙江和广东等省域内台风灾害的未来情景。但是,在较小的单元上,由于数据有限,我们会遇到小样本的信息不完备问题,只能用模糊逻辑和不完备信息来近似推断台风灾害的未来情景。信息不完备时的台风灾害风险,是模糊风险。一旦考虑到全球气候变暖可能对台风发生规律产生影响,或考虑到风险承受体脆弱性的变化,台风灾害风险就有了明显的动态属性。既考虑自然灾害发生的某种统计规律,又考虑自然灾害的动态属性,最简单的自然灾害动态风险形式化模型,是动态的概率风险模型。
不失一般性,我们约定:
·以m记自然致灾力的强度(例如,台风强度、地震动峰值加速度等);
·在研究区域和指定时间段内,m发生的概率密度函数,用p(m)表之;
·风险承受体关于m的脆弱性(在量级为m的致灾力袭击下出现的灾情),用函数f(m)进行描述;
·以向量E记影响灾害风险的可变的综合环境(例如,风险时段和风险承受体周围地貌等);
·以向量C记灾害风险系统中可变的内在属性(例如,全球气候变暖和社会经济发展)。
此时,如果将自然灾害风险视为概率风险,并界定风险的内涵是灾情的期望值时,我们就可以将静态风险模型式(4)[14]改造成式(5)所示的动态风险的形式化模型。
R=∫u00p(m)f(m)dm,
(4)
R(E,C)=∫u00p(m|E,C)f(m,E,C)dm。
(5)
式中:u0为所研究区域中可能发生自然致灾力的最大值。由于非破坏性致灾力不造成灾情,所以动态风险形式化模型中的积分下限可从破坏性致灾力开始。
自然灾害动态风险分析的大量工作,是合理估计条件概率密度函数p(m|E,C),与合理估计动态脆弱性函数f(m,E,C)。对于单参数x的条件概率密度p(m|x)和单参数y的动态脆弱性函数f(m,y),本文建议用正态信息扩散方法,由有条件参数x的历史致灾事件记录和有条件参数y的历史灾情数据记录来生成。
2 用正态信息扩散方法估计条件概率密度
2.1 条件概率密度的本质
在概率论中,有一个基本的概念叫“事件”,是指样本空间上的子集,记为A。而样本空间与随机实验有关。随机实验是指物理或数学的过程:实验可以在相同的情形下重复进行;实验的所有可能结果是明确可知的,并且不止一个;每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前不能肯定这次试验会出现哪一个结果。所有可能结果的集合称为样本空间,记为Ω。每一个可能的结果,称为基本事件,记为ω。亦即是说,Ω由全体ω组成,A是Ω上的子集(可以是直接由一些ω构成的子集,也可以是空集φ,还可以是由子集构成的集合)。
用来测度随机实验中事件发生可能性大小的数值称为“概率”。对事件A的这种测度记为P(A)。这种测度体系必须满足下列4个条件[15]:
(1) 0≤P(A)≤1。
(2) 若A是必然事件,则P(A)=1;若A是不可能事件,则P(A)=0。
(3) 若随机事件Ai与Aj不相容(即两者的交集是空集),则:
P(Ai∩Aj)=0,P(Ai∪Aj)=P(Ai)+P(Aj)。
(4) 若随机事件Ai,i=1,2,…,n,互不相容且可穷举(n个随机事件中必有一个发生),则:

事件A在另外一个事件B已经发生条件下的发生概率,称为在B条件下A的概率,记为P(A|B),当P(B)>0时,它由式(6)进行计算。

(6)
式中:AB指A与B的交集,即AB=A∩B。
例如,假定某地300年内不发生大于7级地震的概率是0.1,在200年内不发生大于7级地震的概率是0.4。该地在过去的200年内没有发生过大于7级地震,求余下的100年内不发生大于7级地震的概率。
解:设A表示该地在过去的300年内没有发生大于7级的地震;B表示该地在过去的200年内没有发生大于7级的地震。
由于过去的300年内没有发生大于7级地震,必定是过去的200年内没有发生大于7级地震,于是,事件A的发生,必有事件B的发生,即A和B同时发生的概率是A发生的概率,P(AB)=P(A)。由式(6),求得余下的100年内不发生大于7级地震的概率为:

由于事件的发生与否互为逆,其概率具有互补关系,即如果A发生的概率是p,则A不发生概率是1-p。由题意知,所研究地区在300年内发生此类地震的概率是0.9,200年内发生大于7级地震的概率是0.6。由于过去的200年内没有发生此类地震,在余下的100年内发生此类地震的概率是1-0.25=0.75,它比在前200年内发生该类地震的概率0.6明显要大。
概率风险分析的核心工作,并非与上述例子类似,即在已知的事件概率基础上,计算形形色色组合事件的概率(故障树恰好是专注于这类工作),而是要估计出基本事件发生的概率。通常,只须研究基本事件ω发生的概率,用组合数学就可计算出事件A发生的概率(这属于古典概型问题)。更进一步来说,一个ω可以对应到一个数,从而将问题转变为对随机变量的研究。
定义2 设Ω为某一试验产生的样本空间,X为定义在Ω上的实函数,即对任一样本点ω∈Ω,X(ω)为一实数,则称X为一个随机变量。
对随机变量X的研究是通过它的具体数值x进行的。因此,在国内外的文献中,在写法上大多不区分一个随机变量和它的具体数值。x既可以代表一个随机变量,也可以代表随机变量的一个值,即一个随机数。如果没有特别的需要,我们总是把一个随机变量写为x。
严格地讲,随机试验中,各个基本事件出现的概率的集合,称为概率分布,只不过引入了随机变量x后变成了关于x的分布,记为P(x)。通常人们所说的“概率分布”,是指“累积概率分布”F(x),即:
F(x)=Prob(X≤x)。
当x是一个连续变量时,常常用概率密度函数p(x)来表达概率分布,即

概率分布表述了随机变量取值的概率规律。概率风险分析的核心工作之一,就是找出这一规律。知道P(x)、F(x)或p(x)中的任意一个,就能推导出另外两个。
当我们不能用定义在Ω上的一维实变量来刻画随机试验的可能结果时,就产生了多维随机向量。条件概率分布,是多维随机向量的产物。例如,登陆研究区域的一次台风,可视为是大自然在该区域进行随机试验的一个结果,它不能用定义在样本空间上的一维实变量来刻画,最少需要用强度和时间这两个变量。当定义2中的X是一个多维随机向量时,相应的概率分布,称为联合概率分布。
定义3 设X=(X1,X2, …,Xn)为n维随机向量,对任一n元实数组x=(x1,x2, …,xn),则F(x1,x2,…,xn)=Prob(X1≤x1,X2≤x2,…,Xn≤xn)称为随机向量X的联合分布函数,也称为联合概率分布。
当我们将条件概率的研究拓展到概率分布的研究时,问题被抽象为:设X=(X1,X2, …,Xn)为n维随机向量,假定已知其中一部分分量的值,在此条件下,其余分量的条件概率分布是什么?
对于离散型随机向量,可以直接由式(6)的条件概率公式去定义条件概率分布。对连续型随机向量,须由概率密度函数去定义条件概率分布。特别地,对于二维连续型随机向量,我们有下述的定义。
定义4 设二维连续型随机向量(X,Y)有概率密度函数p(x,y),则给定X=x时Y的条件概率分布函数是

其中,

(7)
称为y在x条件下的概率密度,简称y的条件概率密度。
由上述的介绍和定义4易知,条件概率密度的本质,是用给定条件x下y的期望

除以联合概率密度分布。关键还在于找出或估计出随机系统的联合概率密度分布函数p(x,y)。
对于一维随机向量,要假定出其概率分布的数学表达式,已经非常困难;对于n维随机向量,更为困难。要用统计方法较准确地估计一个一维概率分布,最少需要30个样本点;二维情况,则需900个样本点。对一个具体的自然灾害动态风险系统,要假定出条件概率密度涉及的联合分布的函数形式,非常困难;要用样本点来估计分布函数中的参数,样本点的个数很难达到要求。因此,在较少样本点的情况下,我们建议采用正态信息扩散的方法,以离散而非解析的方式,近似估计条件概率密度。
2.2 正态信息扩散
分析概率风险的关键之一,是如何有效地学习知识样本。由以往的不利事件记录作为知识样本,采用某种统计方法依其估计事件发生的概率分布,是一种对风险系统的统计学习。在许多情况下,可供学习的知识样本点很少,我们称之为信息不完备。在此条件下,基于传统概率统计方法得出的结果可信度不高,相关风险分析结论的可靠性得不到保证。为了部分弥补信息不完备造成的空白,本文作者在1985年的硕士学位论文中提出了信息分配方法[16],进而在1992年的博士学位论文中将其发展为信息扩散原理[17]。
信息扩散的基本思想,是把一个传统的数据样本点变成一个模糊集合。由于信息扩散的目的是挖掘出尽可能多的有用信息,以此提高系统识别的精度,所以这种技术也被称为模糊信息优化处理技术。最简单的方法是信息分配方法,最简单的扩散函数是正态扩散函数。使用信息扩散方法不需要任何的专家经验,推断出来的模糊风险结论也不会因人而异。
令D={x1,x2,…,xm}是一个给定的样本点集合,U={u}是它的论域(定义域)。将x1,x2,…,xm视为物理化学意义上的分子,将U视为分子扩散的空间,模仿分子扩散,可以给出信息扩散方程,得到一个扩散函数:

(8)
由于μ(x,u)表达的是给定样本点x沿论域点u进行扩散的量值分布,正好与概率论中的正态分布相同,所以μ(x,u)被称为正态扩散函数。其归一化后得到的模糊集,由式(9)表达。

(9)
用式(8)和式(9)对样本点x在U上进行的信息扩散处理,都称为正态信息扩散。由于对模糊集样本点进行统计分析时,须进行归一化处理,让模糊集样本点具有相同的统计地位,所以,式(8)中的第一个因子不影响统计结果。本文提及的正态信息扩散,是指用式(9)进行的扩散。
对正态扩散的计算机仿真实验表明,当每一个信息接收点,从邻近两个样本点扩散得到信息量,等于或多于从其它样本点得到的信息量总和时,扩散估计的结果最好。这一现象被称为两点择近原则。根据此原则和样本点平均距离假设,可以推导出一个计算扩散系数的简单公式[18]:

(10)
这里

信息扩散,只是把没有尺寸大小的样本点变成了有一定影响范围的模糊集。使用这些模糊集来进行统计学习,估计概率分布,还需要学习工具。我们建议用信息矩阵来实现这一目的。
2.3 信息矩阵
设D是一个给定的样本点集合,含有m个样本点,每个样本点有两个分量:x,y。该样本点集合记为:
D={(x1,y1),(x2,y2),…,(xm,ym)}。
(11)

定义5 从卡氏积D×U1×U2到区间[0,1]的一个映射
μ:D×U1×U2→[0,1]
((x,y),u,v)|→μuv(x,y), (x,y)∈D,u∈U1,v∈U2
(12)
称为一个降落公式,如果μ是一个单值映射。
令

(13)
我们说,D赋给了空间U1×U2上的点(u,v)量值为Quv的信息增量。
设uj,j=1,2,…,J和vk,k=1,2,…,K分别是随机变量x的论域U1和随机变量y的论域U2中的离散点。为方便起见,仍分别用U1和U2记它们的离散点的集合,即:
U1={u1,u2,…,uJ},U2={v1,v2,…,vK}
(14)
理论上讲,离散点应尽可能多,但通常根据样本点的精度进行选取,因为太多的离散点除增加计算的工作量外,对提高识别精度帮助不大。也就是说,离散点的选取,并不依赖经验,用样本点间最小距离来控制即可。
定义6 给定样本D={(x1,y1),(x2,y2),…,(xm,ym)},x和y的论域分别是U1和U2。设uj,j=1,2,…,J和vk,k=1,2,…,K分别是U1和U2中的离散点。如果D按式(12)和式(13)赋给了空间U1×U2上的点(uj,vk)量值为Qjk的信息增量,则矩阵
(15)
称为D在U1×U2上的信息矩阵。
当U1,U2均为实数轴上的区间时,通常按等步长取式(14)中的离散点,其步长分别记为Δx和Δy。
我们将式(16)称为二维正态扩散函数,它是卡氏积D×U1×U2到区间[0,1]的一个单值映射,是一个降落公式。
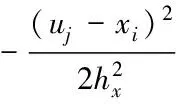
(16)
其中,扩散系数hx和hy用式(10)进行计算。
研究表明,由正态扩散降落公式得到的信息矩阵,较好地展示了原始样本的信息结构,品质较好,且结果不受离散点多少的影响,应用起来很方便。
2.4 用二维信息矩阵估计条件概率密度
当我们不知道一维连续型随机变量概率密度的函数形式时,用随机样本估计概率密度分布最简单的方法是直方图。柱状图(二维直方图)则可用于估计二维连续型随机向量的概率密度分布。由正态扩散产生的二维信息矩阵,能比柱状图更为精确地估计二维概率密度分布,从而用较少的样本点也能较好地估计出条件概率密度。研究表明[19],小样本情况下,正态扩散估计可以比直方图估计减少误差约50%。
用二维正态信息扩散公式(16)生成的信息矩阵式(15),称为原始信息分布,功能相当于频率直方图。令

(17)
则
qjk=Qjk/H,j=1,2,…,J;k=1,2,…,K,
(18)
就是用所给二维随机样本对联合概率分布的一个离散估计,功能相当于相对频率直方图。根据概率密度的定义的,我们可用离散间距Δx和Δy处理qjk,从而得到概率密度值
pjk=qik/(Δx×Δy)。
(19)
由式(7)知,给定X=x时Y的条件概率密度,其实是用各x不变时关于y的积分值去遍除以联合概率密度。用离散逼近连续时,积分转变为求和。于是,给定u=uj时v的条件概率密度是

(20)
3 用正态信息扩散方法估计动态脆弱性函数
3.1 脆弱性函数
脆弱性是人类社会中普遍存在的现象,无非就是易折易碎。在我国南朝刘宋时期的历史学家范晔所编的《后汉书·黄琼传》中就有“峣峣者易缺,皎皎者易污”之述,意为:高的东西容易折损,干净的东西容易变污浊。概括而言,脆弱性是指某个对象,被损伤或被击毁的容易程度。一座破旧的建筑物容易被地震震塌,我们说该建筑物面对地震很脆弱;一个上市企业的股价在大盘急速下跌时跌的并不多,我们说该企业面对股灾不脆弱。对于风险系统而言,我们给出如下的定义:
定义7 设S是风险源,O是风险承受体。O被S损伤或被击毁的容易程度,称为O关于S的脆弱性。
对一个风险系统而言,风险源暴发时其强烈程度往往不同,风险承受体的损伤或击毁程度也就不同。所以,定义中的“容易程度”,通常不是一个数值,而是致灾力强度与损伤程度间的一个函数。例如,活动断层这一地震风险源,其发生破裂时引发地震的震级往往不同。经地震波传播而作用于建筑物的地震动加速度峰值不同,建筑物的破坏也就不同。在地震工程中,加速度与破坏程度之间的函数,称为易损性曲线。同样的加速度,破坏得越严重,建筑物越脆弱。
当脆弱性概念从独立风险承受体向社会系统和生态系统拓展时,人们赋予了它更多的内涵,甚至将重要性(Stakes Value)和恢复力(Resilience)也视为脆弱性的组成部分[20]。在1967-2005间的2286份权威出版物中,脆弱性术语现身了939次[21],近年来脆弱性一词更加热门,但至今脆弱性的研究仍没有重大突破,问题可能在于人们过分纠缠概念和结构,具体的模型和方法受主观因素影响过重,加权处理[22]和层次分析法[23-24]比比皆是。事实上,一旦某个概念被过分拓展,其内核必被冲淡,许多工作就停留在了概念炒作上,不解决任何问题。
我们认为,脆弱性的核心是系统的易损性,研究重点是识别“风险源强度-承受体损伤程度”的关系,即脆弱性函数。这种函数不可能主观给出,而是要进行大量因果关系的研究。特别地,须考虑风险源暴发时其直接作用于承受体的物理量(例如:地震加速度、洪水淹没时间等),亦及承受体当时的状态等多种因素。
为规范本文的表述,我们给出脆弱性函数的定义。
定义8 设S是某种风险源,其暴发时以物理向量x作用于风险承受体O,产生向量v的损伤程度。设x和v的论域分别为U和V,则由O关于S的物理性质所决定的映射
f:U→V
x|→f(x),x∈U,f(x)∈V
(21)
称为O关于S的脆弱性函数,记为v=f(x)。
对于给定的风险承受体,即使进行破坏性实验,也不能从其自身找出脆弱性函数,因为一次损伤实验后,承受体的性质就发生了变化。所以,脆弱性函数通常是对一类风险承受体而言。通常是用该类承受体以往被损伤和被击毁过的资料,经由统计回归而生成。当统计资料过于离散时,脆弱性函数不再是一一映射,而是赋有权重的多值映射。例如,美国政府1991年发表的“未来地震损失估计”研究报告提及的建筑物破坏概率矩阵[25],就是一种以概率为权重的多值映射。此方法引入国内处理相关资料得出的结果,被称为震害矩阵[26]。当统计资料不多时,可用信息扩散方法来改进统计回归。
3.2 用信息矩阵生成离散型脆弱性函数
信息矩阵方法,不仅可以在离散点上识别联合概率分布,还可以在离散点上识别一般的函数关系。
传统上,人们提及函数,主要是指某种解析的数学表达式,其定义域和值域均是在连续的空间中。随着计算机性能的大幅提高,进行系统识别的大量离散算法得以实现。有一定间隔的点组成的论域称为离散论域,这里的离散,英文表述为Discrete。统计学中所说的统计数据离散,则是另一概念,是指统计规律不明显,比较分散,英文表述为Scatter。
不失一般性,我们讨论一个输入x和一个输出y的函数识别问题。记此函数为y=f(x),用给定样本D={(x1,y1),(x2,y2),…,(xm,ym)}进行识别。设这两个分量的离散论域分别是U和V:
U={u1,u2,…,uJ},V=(v1,v2,…,vK)。
(22)
这里的离散点变量符号与式(14)中的完全一样,但论域的名字并不一样。式(14)与式(22)并无关系。由式(16)的二维正态扩散函数处理D,可以在卡氏积U×V上生成信息矩阵Q,如式(15)所示。
这里,生成信息矩阵的方法,与上节中估计条件概率密度用到生成信息矩阵的方法,完全一样,但观察给定样本的视角不一样。上一节中,由m个样本点组成的给定样本D,其两个随机变量被视为具有独立的概率分布,使用D是估计联合分布,我们用信息矩阵Q估计条件概率密度。本节中,仍然是由m个样本点组成的给定样本D,但两个变量被视为具有因果关系,我们用信息矩阵Q识别这一关系(函数)。为了在Q的表述上有所区别,估计条件概率密度用的Q是建立在卡氏积U1×U2上,识别因果关系的Q是建立在卡氏积U×V上,尽管为了书写简捷,我们将U2和V中的元素都记为了v1,v2, …,vK。
我们假定给定样本D中的输入x是风险源暴发时作用于风险承受体的物理量,y是产生的损伤程度。根据定义8,由Q识别出的因果关系,就是脆弱性函数。
式(15)是二维信息矩阵Q的通式,当其是由有因果关系的数据生成时,我们对其进行列向归一化处理,转化为因果型模糊关系矩阵,记为

(23)


(24)


(25)
3.3 用三维信息矩阵生成动态脆弱性函数
当风险承受体O受到动态因素C的影响而致脆弱性发生变化时,对因果关系的识别,需要用到三维信息矩阵。
设D={(y1,c1,z1),(y2,c2,z2),…,(ym,cm,zm)}是给定事件样本。每个样本点记录了所研究种类的风险源S,在动态因素C的影响下,作用于承受体O后产生的后果。设y,c,z的离散论域分别为:
U={u1,u2,…,uJ},V={v1,v2,…,vK},
W={w1,w2,…,wL}。
(26)
使用D在U×V×W上识别出来的函数,是一个动态脆弱性函数。对这种因果关系的识别,需要用到图1所示的三维信息矩阵。

图1 三维信息矩阵示意图
本文建议用式(27)来展开书写三维信息矩阵。这是一种剖面式写法,从动态因素C的不同值v1,v2,…,vK处剖切开,写成K个独立的二维信息矩阵,表达各动态因素值条件下,风险源S作用于承受体O后产生的后果。这K个二维信息矩阵的集合,放入集合符号{ }中,形成一个三维信息矩阵。

(27)

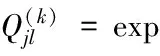
(28)
其中,扩散系数hy,hz和hc用式(10)进行计算。
∀l∈{1,2,…,L},令

(29)

(30)
则

(31)
这是风险承受体损伤程度之风险源O作用和动态因素C影响归一化后的模糊关系矩阵。
同样是根据模糊近似推理,当风险源产生致灾力作用力uj于风险承受体,且承受体动态因素取值为ck时,由式(31)中的R可以得出产生的损伤程度是一个模糊集,如式(32)所示。

(32)

(33)
4 结论和讨论
自然灾害系统的复杂性与系统的动态性密切相关。随着自然环境的变化和人类社会的发展,自然灾害风险必有变化。变化的风险,称为动态风险。人们通过捕捉到的信息和相关数学模型对动态风险的研究,描述的仅仅是认知动态风险,而非真实动态风险。
本文使用动态风险分析基本原理,将概率风险模型中的致灾力概率密度函数拓展为条件概率密度函数,将脆弱性函数拓展为动态脆弱性函数,得到了一个形式化模型,用于分析自然灾害动态风险。其风险内涵是灾害程度的期望,随着综合环境和内在属性的变化而变化。
动态风险分析所需要的联合概率分布函数,更加难以假设出合适的数学解析形式;三维动态脆弱性函数,也不易假设出便于回归学习的解析函数类型。用传统方法估计联合概率分布函数和动态脆弱性函数时,相比静态风险分析只估计概率分布函数和脆弱性函数,都需要多一个数量级的样本点,很难达到要求。在较少样本点的情况下,本文建议采用正态信息扩散的方法,以离散而非解析的方式,近似地估计这两个函数,为自然灾害动态风险分析的形式化模型转化为应用模型提供帮助。
在正态信息扩散模型中,不需要事先假定出两个待识别函数的解析式子,也不需要靠经验选取离散点。分析过程透明,结果可解释性强。以往的大量研究表明,当我们使用正态扩散方法处理给定的随机样本时,在不知样本分布型式且样本量又小的情况下,无论是估计概率分布,还是参数间的因果关系,正态扩散估计的误差均较小。所以,用此模型估计出的条件概率密度函数和动态脆弱性函数均具有一定的可靠性。
动态风险分析的主要工作是“研究综合环境和内在属性变化对风险源和风险承受体的影响”。动态风险的研究,须结合高性能计算机中的离散计算,才有可能解决实际问题。对于高度复杂的,不确定性难以把握的,现实中的动态风险系统,尤其是信息不完备的系统,找一个解析式数学模型加以理想化描述并不难,难的是如何满足理想模型苛刻的条件,使得选用的模型多少有些效果。在自然灾害风险分析中,能写出解析式的理想模型,无论是非线性回归还是眼下流行的Copula模型[28],看起来都很美,但现实很残酷,模型算出结果的可靠性大多经不住深究。
由于篇幅所限,作者将另文虚拟一个台风灾害动态风险分析案例,演示如何应用本文建议的形式化模型。该虚拟案例是在对2000-2006年影响浙江的20个台风和经济损失数据进行分析的基础上,通过合理的假设,用计算机程序创造出来的。
防范于未然是现代防灾减灾的理念。防范于变化中的未然,则是更合理的防灾减灾理念。
世界多元化,风险更多变。一劳永逸式的风险评估受到了挑战。借助互联网强大的信息更新能力,跟踪风险变化、把握动态风险,将逐渐成为可能。
[1]RennO.Emergingrisks:methodology,classificationandpolicyimplications[J].JournalofRiskAnalysisandCrisisResponse. 2014, 4(3): 114-132.
[2]HuangCF.Experimentalriskology:anewdisciplineforriskanalysis[J].HuangHumanandEcologicalRiskAssessment. 2013, 19(2): 389-399.
[3]HolzmannH.Martingaleapproximationsforcontinuous-timeanddiscrete-timestationaryMarkovprocesses[J].StochasticProcessesandTheirApplications. 2005, 115(9):1518-1529.
[4]U.S.ClimateChangeScienceProgramandtheSubcommitteeonGlobalChangeResearch.WeatherandClimateExtremesinaChangingClimate.RegionsofFocus:NorthAmerica,Hawaii,Caribbean,andU.S.PacificIslands[R].Washington,DC:UNTDigitalLibrary, 2008.http://digital.library.unt.edu/ark:/67531/metadc12026/.AccessedDecember9, 2013.
[5] 孙殿阁,孙佳,王淼,等. 基于Bow-Tie技术的民用机场安全风险分析应用研究[J]. 中国安全生产科学技术,2010,6(4): 85-98.
[6]HuangCF,RuanD.Fuzzyrisksandanupdatingalgorithmwithnewobservations[J].RiskAnalysis, 2008, 28(3): 681-694.
[7]GobleR,BierVM. 2013.Riskassessmentcanbeagame-changinginformationtechnology—buttoooftenitisn’t[J].RiskAnalysis, 2013, 33(11): 1942-1951.
[8] 庞西磊. 自然灾害动态风险分析基本模式的探讨及其应用研究[D]. 北京: 北京师范大学, 2012.
[10]BerendR,SchumacherJM.TimeconsistencyconditionsforacceptabilitymeasureswithanapplicationtoTailValueatRisk[J].InsuranceMathematicsandEconomics,2007,40(2): 209-230.
[12]BlaikieP,CannonT,DavisI,Wisner,B.AtRisk:NaturalHazards,People’sVulnerability,andDisasters[M].London:Routledge, 1994.
[13]黄崇福. 自然灾害动态风险分析基本原理的探讨[J]. 灾害学, 2015, 30(2):1-10.
[14]黄崇福. 综合风险评估的一个基本模式[J]. 应用基础与工程科学学报,2008, 16(3): 371-381.
[15]BillingsleyP.ProbabilityandMeasure[M].NewYork:Wiley, 1979.
[16]黄崇福. 地震震害面积估计[D]. 哈尔滨:国家地震局工程力学研究所,1985.
[17]黄崇福. 信息扩散原理与计算思维及其在地震工程中的应用[D].北京:北京师范大学,1992.
[18]黄崇福. 自然灾害风险分析与管理[M]. 北京:科学出版社,2012.
[19]HuangCF,ShiY.TowardsEfficientFuzzyInformationProcessing——UsingthePrincipleofInformationDiffusion[M].Heidelberg:Physica-Verlag(Springer), 2002.
[20]DeckO.,VerdelT.andSalmonR.Vulnerabilityassessmentofminingsubsidencehazards[J].RiskAnalysis, 2009, 29(10): 1381-1394.
[21]JanssenMA,SchoonML,KeW.andBörnerK.Scholarlynetworksonresilience,vulnerabilityandadaptationwithinthehumandimensionsofglobalenvironmentalchange[J].GlobalEnvironmentalChange, 2006, 16 (3): 240-252.
[22]杜晓燕,黄岁樑. 天津地区农业旱灾脆弱性综合评价及区划研究[J]. 自然灾害学报, 2010, 19(5):138-145.
[23]孙蕾. 沿海城市自然灾害脆弱性评价研究[D]. 上海:华东师范大学,2007.
[24]杨洋. 辽宁省沿海城市自然灾害脆弱性评价研究[D]. 大连:辽宁师范大学, 2011.
[25]RojahnC,SharpeRL.ATC-13:EarthquakeDamageEvaluationDataforCalifornia[R].RedwoodCity,California:AppliedTechnologyCouncil, 1985.
[26]尹之潜. 地震灾害损失预测研究[J]. 地震工程与工程振动, 1991,11(4): 87-96.
[27]黄崇福. 自然灾害风险分析的信息矩阵方法[J]. 自然灾害学报,2006, 15(1): 1-10.
[28]NelsonRB.AnIntroductiontoCopulas[M].NewYork:Springer, 2006.
AFormalModelforDynamicRiskAnalysisinNaturalDisasters
Huang Chongfu1, 2, 3
(1.StateKeyLaboratoryofEarthSurfaceProcessesandResourceEcology,BeijingNormalUniversity,Beijing100875,China; 2.KeyLaboratoryofEnvironmentalChangeandNaturalDisaster,MinistryofEducationofChina,BeijingNormalUniversity,Beijing100875,China; 3.AcademyofDisasterReductionandEmergencyManagement,MinistryofCivilAffairs&MinistryofEducation,Beijing100875,China)
Accordingtothebasicprincipleofdynamicriskanalysisinnaturaldisasters,basedonthemodelforprobabilityrisk,thisarticledevelopsaformalmodeltoanalyzedynamicriskinnaturaldisasters.Therisk,couplingoftheconditionalprobabilitydensityfunctionandthedynamicvulnerabilityfunctiontogether,iswiththechangeofintegratedenvironmentalandintrinsicpropertiesvary.Wesuggestthattheprobabilitydensityfunctionandthedynamicvulnerabilityfunctionwouldbeestimatedbyusingnormalinformationdiffusionmethod.Theestimatesofthetwoimportantfunctionsdonotrelyonanyassumptions.Theanalysisprocessistransparent.Theresultcanbeinterpretive,andhascertainreliability.
dynamicrisk;naturaldisaster;densityfunction;vulnerabilityfunction;informationdiffusion
2015-01-20
2015-02-15
国家重大科学研究计划“全球变化与环境风险演变过程与综合评估模型”(2012CB955402)
黄崇福(1958-),男,云南个旧人,博士,教授,博士生导师,中心主任,研究方向为自然灾害风险分析. E-mail: hchongfu@bnu.edu.cn
X43
A
1000-811X(2015)03-0001-09
10.3969/j.issn.1000-811X.2015.03.001
黄崇福. 自然灾害动态风险分析的一个形式化模型[J].灾害学, 2015,30(3):001-009. [Huang Chongfu. A Formal Model for Dynamic Risk Analysis in Natural Disasters [J].Journal of Catastrophology, 2015,30(3):001-009.]

