随机介质理论下隧道围岩渐进破坏过程数值实验研究*
商拥辉,李 航,张 波,方前程
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中大路桥集团有限公司,黑龙江 哈尔滨 150300;3.沈阳市城乡建设委员会,辽宁 沈阳 110013;4.黄淮学院 建筑工程学院,河南 驻马店 463000)
随机介质理论下隧道围岩渐进破坏过程数值实验研究*
商拥辉1,4,李 航2,张 波3,方前程4
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中大路桥集团有限公司,黑龙江 哈尔滨 150300;3.沈阳市城乡建设委员会,辽宁 沈阳 110013;4.黄淮学院 建筑工程学院,河南 驻马店 463000)
将强度折减法引入到隧道围岩安全评价中,结合“浅埋暗挖快速施工双线小间距隧道、盾构下穿立交结构隧道和结构面含有节理、不规则裂隙的山体公路隧道”等工程实例,借助材料真实破坏分析软件RFPA-2D,建立每个强度折减系数下的有限元模型。模型采用了黏弹性人工边界来消除边界条件对计算精度的影响,并借助随机介质理论实现了围岩细观结构单元的非均值性和随机分布的缺陷,揭示了不同工况下隧道围岩的动态渐进破坏过程、基元相变损伤演变机理和岩体结构面破坏特征,认为隧道围岩的宏观破坏是由岩体非线性材料细观单元的非均值性造成的,计算结果借助不同折减步中裂纹发展趋势和单元破坏的数量判断隧道围岩是否失稳破坏,并计算出具有安全储备意义上的安全系数。同时,结合ABAQUS和RFPA-2D两种不同有限元模型,对比分析了随机介质理论和连续介质理论结合强度折减法在隧道围岩稳定性评价中的差异。
随机介质;强度折减;隧道围岩;破坏过程;安全系数
强度折减法最早于20世纪70年代 的英国科学家Zienkiewicz等提出,并最早用于边坡稳定性评价中[1-2]。该方法通过不断折减岩体材料的强度参数,能够得到岩土材料极限平衡状态时的破坏位置、破坏性质,并得到稳定安全系数[3-7]。近年来,伴随着计算机水平、强度折减法力学破坏机理的不断发展,如:郑颖人和赵尚毅等[6-9]从理论上对安全系数的定义、屈服准则和流动法则的选取、边坡破坏判据的标准、岩土参数的取值和如何提高计算精度的措施做了大量研究,为强度折减法在隧道中的应用提供了理论基础。
强度折减法借助传统数值计算软件,对隧道开挖围岩稳定性的判断主要结合围岩的位移和塑性区的发展,如:李秀地等[10]把强度折减法和有限差分软件FLAC3D结合,对沉管海底隧道的安全稳定性进行分析;江阿兰等[11]把强度折减法和有限元软件ABAQUS结合,对沈阳地铁某标段浅埋暗挖快速施工隧道的安全稳定性进行分析。以往研究主要从岩体宏观上是连续均值介质着手,而张波、张黎明、商拥辉[12-14]等结合真实破坏分析软件RFPA2D,结合随机介质理论[12-18],从岩体材料的微观结构出发,利用韦伯随机分布函数来实现岩体细观结构单元的非均值性和缺陷,结合工程实例,对隧道围岩强度折减过程裂纹的发展过程进行模拟,借助折减步中声发射规律了解细观单元破坏过程中能量的变化过程。该方法较传统方法更直观、简单。
强度折减法在计算隧道围岩稳定安全系数时,应注意隧道是整体失稳还是局部失稳。隧道受剪破坏的安全系数也可分为两种[15]:①隧道整体失稳,其相应的是整体安全系数;②隧道局部失稳,一般发生在节理裂隙岩体中,其相应的是局部安全系数,也可通过块体平衡等方法求解。
本文借助真实破坏分析软件RFPA2D,建立随机介质理论下的非均值模型,对“浅埋暗挖快速施工双线小间距隧道、盾构下穿立交结构隧道和含有复杂裂隙山体公路隧道”等复杂环境条件下隧道的安全系数进行计算,重在揭示复杂隧道不同工况下围岩的破坏机制,能够为类似隧道工程围岩的安全稳定性评价提供一种思路。
1 强度折减法及安全系数
安全系数的定义Fs也称稳定系数,是边坡稳定性研究中的一个重要概念。传统边坡稳定性的分析中安全系数定义为滑动面的抗滑力与下滑力之比。隧道计算中基于强度储备概念的安全系数Fs定义为[6]:当岩土体的抗剪强度参数c和φ分别用其临界强度参数c′和φ′所代替后,岩土体将处于临界平衡状态,其中,

(1)
由折减系数和失稳时当前的计算步可以求围岩初始时(未折减时)强度储备安全系数,安全系数Fs的计算公式如下:
Fs=1/(1-n×step)。
(2)
式中: 为折减系数,取0.02;step为折减破坏失稳时当前的计算步。
2 复杂环境条件隧道工况分析
2.1 双线小间距浅埋暗挖隧道
某市地铁2号线某区间起讫里程为:右线K0+0.000~K1+390.5,全长1 390.5m,区间为单洞单线马蹄形断面,轴线平均间距15m,线路纵向呈“∨”型坡,区间隧道覆土厚度为10~12m,最小线间距为12.5m,隧道埋深10.15m。地下水位平均埋深为14.5m左右。区间土体主要参数详表1所示。

表1 土层力学参数
2.2 盾构下穿立交结构隧道
某市地铁2号线在K1+110~K1+700设计里程范围下穿立交桥。隧道采用土压平式盾构机施工,双线隧道间距13~50m。隧道结构底最大埋深约30.12m,最小埋深14.98m。立交桥基础为人工挖孔桩,埋深13.3~17.2m,桩径2.0~2.5m值均下穿立交结构平面图见图1。

图1 盾构下穿立交结构平面图
根据盾构下穿立交结构工况,研究区断面可以分为以下几类。①不含桩基的截面。这类截面较多,占据整个研究区95%以上。②桩基距离隧道一侧大于10m的截面。由于桩基距离隧道较远,隧道开挖时受桩基荷载的影响较小,计算时可忽略不计。③桩基距离隧道一侧3~10m的截面,该类截面仅一个。④桩基距离隧道一侧0~3m的单桩截面,该类截面仅一个。各断面基本信息详见表2,土层参数详见表3。

表2 各断面基本信息统计表

表3 土层力学参数
2.3 结构面含有节理、裂隙隧道
重庆至长沙高速公路某区间线路穿越山体而修建隧道。该区间山区岩石结构面较为复杂,主要表现为水平结构面,30°、45°倾角结构面和含有复杂裂隙的结构面,裂隙长度在3~6m。计算选取断面具体信息详见表4。

表4 各断面基本信息统计表
3 随机介质理论下非均值模型
RFPA-2D建模中,基元是代表物理力学性质特征的最小介质单元,围岩渐进破坏过程就是基元受压或拉作用下,不断损伤引起的裂缝萌生、扩展和破坏的过程[15-17]。模型通过Weibull随机分布函数实现材料的非均值性和缺陷。

(3)
式中:φ(x)为具有弹性模量E的基元的统计数量。由式(3)统计分布构成的基元组成一个样本空间,在均值E0不变的情况下,由于m值的差别,积分空间分布却不一样。这些基元构成的岩石类介质的细观平均性质可能大体一致(E0相同),但是由于细观结构的无序性,使得基元的空间排列方式有显著的不同。这种细观上的无序性正好体现了岩石类介质独特的离散性特征。
模型中用弹性损伤力学的本构关系对土体细观单元的力学性质进行描述。依据等价应变原理,通过无损材料中的名义应力对受损材料非线性本构关系进行描述,即:

(4)
式中:σ为应力;ε为应变;E0为初始弹性模量;E为损伤后的弹性模量;D为损伤参量。在单轴应力状态下表示材料体积单元中存在的微裂纹的比率,当D=0时,材料无损伤,当D=1时,材料完全损伤。
计算中采用带有拉伸截断的摩尔-库仑准则。当细观单元的最小主应力超过其单轴拉伸强度时细观单元发生拉伸破坏,此时损伤演化方程:
(5)
式中:σrt为细观单元拉伸破坏时的残余强度;εt0为细观单元拉伸破坏的最小主应变阈值;εtu为细观单元分离的最小主应变阈值。
根据工况和RFPA-2D软件特点,“盾构下穿立交结构隧道和结构面含有节理、不规则裂隙的山体公路隧道”模型尺寸选取60m×60m,每个单元尺寸为300mm×300mm,整个模型共有40 000个单元数。模型两侧限制水平方向位移,底边为固定约束。模型采用韦伯分布函数对基元进行随机赋值,通过均值度来反映材料的离散性,均值度系数m值越高,基元离散程度越低,根据材料性质的不同,土体材料取m=3,岩体材料取m=100。介质的弹性模量空间分布形式见图2。

(a)m=2 (a)m=4 (a)m=5
4 计算结果分析
为了对比分析随机介质理论和连续介质理论结合强度折减法在隧道围岩稳定性评价中的差异,对于“浅埋暗挖双线小间距隧道”,利用有限元分析软件ABAQUS计算。结合文献[5-15],模型尺寸取80 m×40 m。土体和衬砌等区域采用四节点平面应变缩减积分单元(CPE4R),锚杆采用桁架单元(T2D2)。开挖面土体、衬砌、注浆层采用扫掠网格划分,其它部分采用结构网格划分。模型两侧限制水平方向的位移,底边限制水平和竖直方向的位移。土体采用Mohr-Coulomb非线性本构模型。
计算中通过以下三个方面判断隧道围岩是否破坏:①有限元静力平衡计算不收敛;②以塑性区或者等效塑性应变贯通隧道;③滑动面土体应变和位移发生突变使土体无限移动发展。滑动面塑性区贯通是隧道破坏的必要不充分条件,由于滑体出现无限移动和计算不收敛同时出现,可将有限元计算是否收敛或者滑面节点塑性应变和位移突变作为隧道破坏的依据。
图3(1)是浅埋暗挖双线小间距隧道不同折步下隧道围岩的位移和塑性区分布云图。从图3(1)可以看出:随着强度折减,隧道洞口上方位移开始变大,折减系数为2时,隧道洞口上方位移开始出现贯通趋势,强度折减系数为2.75时,位移贯通隧道洞口;位移变化的同时,塑性区随强度折减也在不断扩展,最先位于洞口两侧水平区域,折减系数为2.75时,塑性区贯通隧道,且此时计算不收敛,故此双线小间距隧道安全系数为2.75。

(a)n=1位移云图 (b)n=1.25位移云图 (c)n=1.75位移云图 (d)n=2位移云图

(e)n=2.5位移云图 (f)n=2.75位移云图 (g)n=1塑性区云图 (h)n=1.25塑性区云图

(i)n=1.75塑性区云图 (j)n=2塑性区云图 (k)n=2.5塑性区云图(m)n=2.75塑性区云图(1)工况1:浅埋暗挖双线小间距隧道

(a)隧道开挖 (b)n=25-40 (c)n=25-44 (d)n=25-48(2)工况2:桩基距离隧道洞口一侧较近隧道(不同折减步剪应力)

(a)隧道开挖 (b)n=23-28 (c)n=23-32 (d)n=23-40(3)工况3:单桩位于隧道洞口上方隧道(不同折减步剪应力)

(a)隧道开挖 (b)n=19-31 (c)n=19-35 (d)n=19-39(4)工况4:双桩位于隧道洞口上方隧道(不同折减步剪应力)

(a)n=3 (b)n=17 (c)n=20-15 (d)n=20-21(5)工况5:含有水平结构面的隧道(不同折减步剪应力)

(a)初始应力平衡 (b)n=3 (c)n=5 (d)n=12-7(6)工况6:含有30°倾角结构面的隧道(不同折减步剪应力)

(a)初始应力平衡 (b)n=16 (c)n=18-20 (d)n=18-25(7)工况7:含有45°倾角结构面的隧道(不同折减步剪应力)

(a)初始应力平衡(b)n=2 (c)n=11-28 (d)n=11-49(8)工况8:含有不规则裂隙结构面的隧道(不同折减步剪应力)
强度折减发结合传统有限元软件评价隧道围岩失稳的判据相对较多,而采用真实破坏过程分析软件RFPA-2D时,采用每一折减计算步中出现单元破坏数最多时的时刻作为岩体失稳的临界点。计算中将单元的强度以线性关系按一定比例逐渐折减,每折减一次,有限元计算程序进行迭代计算,寻找外力与内力的平衡,同时进行破坏分析,直到隧道围岩发生失稳破坏。可以借助不同折减步中裂纹发展趋势和单元破坏的数量判断隧道围岩是否失稳破坏。
图3(2~8)是“盾构下穿立交结构隧道和结构面含有节理、不规则裂隙的山体公路隧道”不同折减步时隧道围岩的剪应力图。通过图3(2~8)可以直观地看到隧道围岩的裂纹生成、扩展并最终贯通的全过程。图3(2)中折减步为25-48,25是总的折减步数,48代表第25步中的第48步,也就是“步中步”,“步中步”的概念是岩体强度在每一步进行折减,通过应力分析得到所有单元的应力场,然后,根据破坏准则来判断单元是否破坏,假如该加载步有单元破坏,则按照以上的弹性本构关系计算性能弱化之后的弹性模量,进行在外部荷载不变的情况下的重新计算,以反映由于单元性能弱化及破坏所造成的应力重分布,直到该加载步没有新的单元破坏为止。然后岩体强度继续进行折减,进入下一步的分析。
盾构下穿立交结构的隧道断面,由于桥基荷载的影响较大,隧道开挖前,已经采取了“型钢”加固措施(桥基荷载等效传递到地面,具体工艺可参考献[13]),文中模拟是在加固之后。从图3可以看出:桥基距离隧道洞口一侧时,受桥基荷载影响较小,强度折减到n=25~40时,裂纹基本位于隧道洞口两侧45。区域,桩端附近区域出现裂纹较少,折减到n=25~48时,裂纹扩展成型的大裂隙,隧道围岩失稳破坏;单桩位于隧道洞口上方时,受荷载影响略大,强度折减到n=23~40时,成型的裂纹贯通隧道;而双桩位于隧道洞口上方时,受到荷载影响最大,强度折减到n=19~39时,裂纹贯通隧道,围岩失稳破坏。
岩体中含有水平结构面隧道,由于隧道开挖的位置在两条结构面上面,在隧道与结构面相交的位置,产生了明显的应力集中,这主要是由于结构面的弹性模量和强度较低造成的,而结构面与隧道的位置恰巧也是隧道形状本身容易产生应力集中的部位,裂纹贯通隧道,围岩最终破坏的折减步为n=20~21。岩体中含有30°倾角结构面隧道,岩体强度折减中隧道围岩的渐进破坏方式如图3(6)。从图3(6)可以看到:与含有水平结构面的模型相同的是,在隧道与结构面相交的位置,产生了明显的应力集中,且由于结构面左倾,在隧道左侧拱肩部位同样产生了较大的应力,这是因为结构面距离隧道很近的结果,而在这一部位,由于受到竖直地应力和水平地应力的共同作用,隧道围岩产生了拉破坏;最终隧道失稳破坏的折减步为n=12~7。岩体中含有45°倾角结构面隧道,岩体强度折减中隧道围岩的渐进破坏方式如图3(7)。从图3(7)可看出:含有45°倾角结构面的最终破坏可以看出,与含有30°倾角结构面类似,同样是在隧道左侧拱肩部位和右侧拱脚部位产生了破坏。由此可以看出,在还有结构面的隧道设计和施工中,沿着垂直于结构面方向是应该加强支护的危险部位,对这些部位的支护对于增加隧道围岩的稳定性会具有明显的作用;最终隧道失稳破坏的折减步为n=18~25。含有复杂裂隙的隧道,无论是在开挖还是支护之后,隧道周围的围岩应力没有发生太大的变化。这是因为岩体裂隙群基本设置在隧道的上方,而这些裂隙群承担了上部岩体的应力,即隧道上方的裂隙群发生的应力集中现象,承担了更多的地应力,而减少了隧道围岩的受力,但这并没有提高围岩的整体稳定性,隧道围岩最终破坏的折减步数为n=11~28。
综上计算结果,各断面安全系数汇总详见表5。
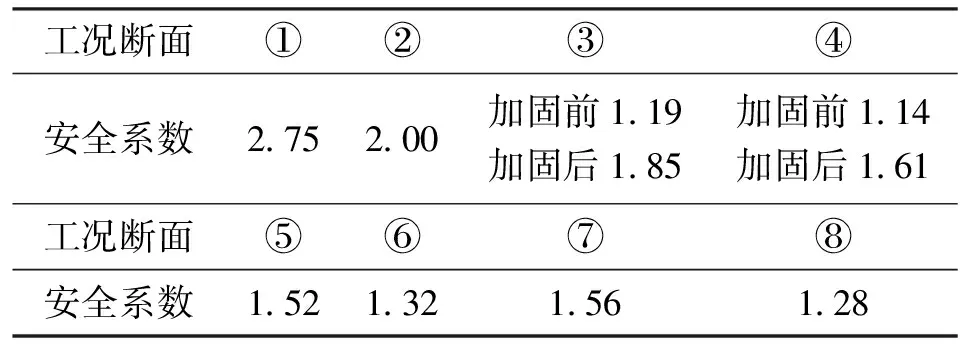
表5 断面安全系数汇总表
5 结论
(1)将有限元强度折减法引入到隧道工程中,是围岩安全评价的一种新趋势。结合传统有限元软件,可以借助围岩位移、塑性区和计算不收敛作为判据;而结合RFPA-2D可以直观通过不同折减步中裂纹发展趋势和单元破坏的数量判断隧道围岩是否失稳破坏,相比更简单、易操作。
(2)通过weibull随机分布函数实现岩体细观单元的非均值性和缺陷,可以揭示不同工况下隧道围岩的动态渐进破坏过程、基元相变损伤演变机理和岩体结构面破坏特征,认为隧道围岩的宏观破坏是由岩体非线性材料细观单元的非均值性造成的。
(3)桩基荷载对隧道围岩裂纹的发展和安全有不同程度的影响。单桩距离隧道断面较远的断面,影响较小,安全系数达到2;单桩和双桩位于隧道洞口上方的断面,影响较大,隧道安全系数较低,分别为1.19和1.14,采取加固措施后安全系数依次提高到1.85和1.61。
(4)岩体含有水平结构面,30°、45°倾斜结构面和不规则裂隙隧道断面,由于结构面和裂隙处的岩体强度较低,隧道安全系数较低,稳定性较差,依次为1.52、1.32、1.56和1.28,施工中要采取相应加固措施。
(5)通过隧道渐进破坏过程模拟,得出隧道破坏以剪切破坏和拉破坏为主,还可以借助裂纹发展趋势,预判隧道围岩的安全稳定性。
[1] 韩爱民,李建国,傅国利,等.基于有限差分强度折减法的多级边坡破坏模式研究[J].工程地质学报,2007,15(6):784-788.
[2] 钟志辉,杨光华,张玉成,等.基于局部强度折减法的土质边坡位移研究[J].岩土工程学报,2011,8(Supp.1): 196-201.
[3] 赵尚毅,时卫民,郑颖人.边坡稳定性分析的有限元法[J].地下空间,2001,21(5):450-454.
[4] 赵尚毅,郑颖人,邓卫东.用有限元强度折减法进行岩质滑坡稳定性分析[J]. 岩石力学与工程学报,2003,22(2):254-260.
[5] 郑颖人,赵尚毅,邓卫东.岩质滑坡破坏机制有限元数值模拟分析[J]. 岩石力学与工程学报,2003,22(12):1943-1952.
[6] 赵尚毅,郑颖人,张玉芳.极限分析有限元法讲座—Ⅱ:有限元强度折减法中边坡失稳的判据探讨[J].岩土力学, 2005, 26(2): 332-336.
[7] 郑颖人,叶海林,黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报,2009, 28(8):1714-1723.
[8] 郑颖人,赵尚毅,张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学,2002,4(10):57-61.
[9] 张鲁渝,郑颖人,赵尚毅,等.有限元强度折减系数法计算土坡稳定安全系数的精度研究[J].水利学报,2003(1): 21- 27.
[10]李秀地,郑颖人等.沉管海底隧道强度折减法分析探讨[J].岩土工程学报,2013(10):1887-1889
[11]江阿兰,张波,郑继强. 地铁浅埋暗挖快速施工研究和土体稳定性分析[D].大连:大连交通大学,2012:10-11
[12]张波,李航.复杂地质条件下隧道破坏过程研究[D].沈阳:沈阳建筑大学,2011:5-25.
[13]张波,商拥辉.基于盾构下穿立交结构围岩整体稳定性分析[D].大连:大连交通大学,2012:5-80.
[14]张黎明,郑颖人,王在泉,等.有限元强度折减法在公路隧道中的应用探讨[J].岩土力学,2007,28 (1):97 -102.
[15]唐春安,李连崇,李常文,等.岩土工程稳定性分析RFPA强度折减法[J]. 岩石力学与工程学报, 2006,25(8): 1522-1530.
[16]朱万成,唐春安,杨天鸿,等. 岩石破裂过程分析(RFPA 2D)系统的细观单元本构关系及验证[J].岩石力学与工程学报,2003,22(1):24-29.
[17]Zienkiewicz O C, Humpheson C, Lewis R W. Associated and non-associated visco-plasticity and plasticity in soil mechanics [J]. Geostechnique, 1975, 25(4):671-689.
[18]Jeong S,Kim B,Won J,et al. Uncoupled analysis of stabilizing piles in weathered slopes[J]. Computers and Geotechnics,2003,30(8):671-682.
[19]Ausilio E, Conte E, Dente G. Seismic stability of reinforced slopes[J]. Soil Dynamics and Earthquake Engineering, 2000, 19(3): 159-172.
[20]Manzari M T, Nour M A. Significance of soil dilatancy in slopestability analysis [J]. Journal of Geotechnical and Geoenviron-mental Engineering, ASCE, 2000, 126(1): 75-80.
[21]Ugai K. A method of calculation of total factor of safety of slopes by elaso-plastic FEM [J]. Soils and Foundations, 1989, 29(2):190-195.
Numerical Experiment Research on the Progressive Failure Process of the Surrounding Rock of the Tunnel under the Stochastic Medium Theory
Shang Yonghui1, 4, Li Hang2, Zhang Bo3and Fang Qiancheng4
(1.SchoolofCivilEngineering,CentralSouthUniversity,Changsha410075,China;2.CuhkLuqiaoGroupCompany,Harbin150300,China; 3.ShenyangUrbanandRuralConstructionCommittee,Shenyang110013,China; 4.InstituteofArchitectureandEngineering,HuanghuaiUniversity,Zhumadian463000,China)
Thestrengthsubtractionisintroducedtosafetyevaluationoftunnelsurroundingrock,combiningwith“theshallowtunnelrapidconstructiondoublesmallspacingtunnels,wearinterchangestructureundertheshieldtunnelandthesurfaceofthestructurecontainingjoint,irregularfissureofmountainhighwaytunnel”engineeringexamples,usingrealdamageofmaterialanalysissoftwareRFPA-2D,thefiniteelementmodelofeachstrengthreductionfactorissetup.Viscoelasticartificialboundaryisadoptedtoeliminatetheinfluenceofboundaryconditionsonthecalculationprecisioninmodel,andthemodelachievesthemesoscopicstructureunitofsurroundingrockofthemeanandthedefectsofrandomdistributionbymeansofrandommediumtheory,italsorevealsthedynamicgradualdamageprocessofsurroundingrock,theprimitivephasechangedamageevolutionmechanismandcharacteristicsofrockmassstructuralplaneunderdifferentworkingconditions,themesoscopicdamageofsurroundingrockisthoughttobecausedbynonaverageofrocknonlinearmaterialmacroscopicunit,thecalculationresultsjudgedinfailureoftunnelsurroundingrockwithdifferentstepreductionincrackdevelopmenttrendsandthenumberofcelldamage,andcalculatessafetyfactorinthesenseofthesafetyreserve.Atthesametime,combiningABAQUSwithRFPA-2Dtwodifferentfiniteelementmodels,comparativelyanalyzingtherandommediumtheoryandcontinuumtheorycombiningstrengthsubtractionindifferencesoftheevaluationofsurroundingrockstability.
randommedium;strengthreduction;tunnelsurroundingrock;failureprocess;safetycoefficient
2014-12-06
2015-01-25
湖南省自然科学基金资助项目(11JJ3051);湖南省教育厅资助科研项目(13C307)
商拥辉(1982-),男,河南汝南人,博士,主要从事地下结构、轨道交通及地质灾害风险评估方面的研究.E-mail:mlpeter@163.com
张波(1979-),男,辽宁营口人,博士后,高级工程师,从事地下结构及轨道交通工程建设及管理方面的研究. E-mail:zbsyhfblw@aliyun.com
U45;X43
A
1000-811X(2015)03-0047-07
10.3969/j.issn.1000-811X.2015.03.010
商拥辉,李航,张波,等. 随机介质理论下隧道围岩渐进破坏过程数值实验研究[J].灾害学, 2015,30(3):047-053. [Shang Yonghui, Li Hang, Zhang Bo,et al. Numerical experiment research on the progressive failure process of the surrounding rock of the tunnel under the stochastic medium theory[J].Journal of Catastrophology, 2015,30(3):047-053.]

