基于权重的WKFCM聚类算法在泥石流评价中的应用*
李 炫,范建容,张建强
(1.中国科学院·水利部成都山地灾害与环境研究所,四川 成都 610041;2.中国科学院大学,北京 100049)
基于权重的WKFCM聚类算法在泥石流评价中的应用*
李 炫1,2,范建容1,张建强1
(1.中国科学院·水利部成都山地灾害与环境研究所,四川 成都 610041;2.中国科学院大学,北京 100049)
泥石流的形成受地形条件、地质构造、气象水文等多种因素的综合影响,不同区域的泥石流灾害在空间分布上具有一定的差异性和相似性,聚类分析能够识别出这种相似的特性。针对KFCM聚类算法没有考虑到不同影响因子对于泥石流灾害的贡献程度不同的缺陷,引入权重的概念,对KFCM算法进行改进,选取沟床比降、流域面积、构造系数、冰川坡度、岩性系数、平均坡度、最大淤积、可移方量、冰川面积与流域面积比9个因素作为区域内冰川泥石流危险性的评价指标,采用层次分析法求取各个评价指标的权重值,以西藏境内30条具有良好工作基础的冰川泥石流沟为研究对象,探究改进后的WKFCM聚类算法在泥石流危险性评价中的应用。结果表明,改进后的算法可以避免传统评价方法阈值确定时的主观不确定性,将其应用在泥石流危险性评价中是有效可行的。
权重;WKFCM聚类算法;泥石流灾害;评价
泥石流的是一种极为复杂的自然现象,它在暴雨、融雪等外界条件的激发下产生,来势迅猛,运动速度很快,暴发突然,能量巨大,其携带的大量的石块和碎屑物质具有冲击力强和破坏性大的特点,给山区的经济发展和山区人民的生命安全都带来了巨大威胁。泥石流危险性评价是灾情评估、预测、防灾救灾的基础[1],它对防范泥石流灾害的发生,减少泥石流灾害带来的损失,以及区域的规划建设都具有非常重要的意义。
长期以来,随着对泥石流研究的不断深入,泥石流危险性评价经历着从定性到定量的发展,多因子综合评价模型、信息量模型、神经网络模型、多元回归模型、灰色关联度模型、模糊数学等等方法都在泥石流危险性评价中有着较好地应用[2-4]。但是这些评价方法,往往都需要足够的灾害训练样本做基础,在样本不足或缺失的情况下就难以实现准确的评价。聚类分析是指按照数据之间某种相似程度的度量,对数据进行归类,使得被划分到同一类的对象相似度最大,不同类别的相似度最小。不同区域的泥石流灾害在空间分布上存在着一定的相似性和差异性[5],将聚类分析方法应用在泥石流评价中能够较好的识别出这种相似特性,算法含义清晰,能够对研究对象进行定量评价[6]。国内很多学者对聚类分析方法在灾害评价中的应用做了大量的尝试,丁明涛等应用k-means聚类方法实现了三江并流区泥石流危险性评价[7];王建国等应用聚类分析的方法实现了抚顺地区地质灾害综合评价,有效地确定了不同地质灾害的类型区[5]。
聚类分析方法为泥石流等地质灾害的评估提供了一种新的思路。但对于泥石流评价来说,传统的聚类方法并没有考虑到不同影响因子对泥石流的贡献程度的不同,评价的精度难免会受到影响。本文在前人的基础之上,选取西藏境内具有良好工作基础的30条冰川泥石流沟为研究对象,考虑到不同影响因子对泥石流灾害的权重的不同,对KFCM算法进行改进,引入权重的概念形成WKFCM聚类方法,探讨基于权重的WKFCM聚类算法在泥石流危险性评价中的应用。
1 理论基础
1.1 KFCM聚类算法
将聚类方法应用到泥石流危险性评价中就是将不同危险性的泥石流沟进行识别和归类。考虑一个样本集X={x1,x2,…,xn},n为泥石流沟条数,其中x1={xi1,xi2,…,xik}为K维向量,K为泥石流灾害的影响因子, 建立n×K维向量,KFCM聚类算法就是把n个向量xi(i=1, 2,…,n)分为c个组, 使得非相似性指标的价值函数达到最小。KFCM聚类算法的具体描述如下[8]。
(1)根据目标函数把数据集X划分成c类。

(1)
式中:m为模糊加权指数,它的最佳取值范围为[1.5,2.5];φ是到高维特征空间的非线性映射,满足式(2)。uij表示数据j隶属于i类的隶属度,取值在0~1之间,vj表示聚类中心。
(2)依据式(2)实现从低维到高维的映射。
‖φ(xi)-φ(vj)‖2=K(xi,xi)-2K(xi,vj)+K(vj,vj),
(2)
式中:K为核函数。在本文中,采用高斯核函数,如式(3)所示。

(3)
式中:‖x-y‖2表示x,y两点的欧几里德距离,σ是高斯参数。
依据上述公式,KFCM聚类算法的数学描述可以表示为:

(4)

对目标函数运用拉格朗日算法导出聚类中心vj和隶属度uij的计算公式为:

(5)

(6)
泥石流危险性评价的过程就是通过迭代的方法求解式(5)、(6)中的聚类中心vj和隶属度uij,使得目标函数J最小,以达到分类目的,然后对各个类别赋予不同的危险度,从而实现泥石流沟危险性评价。
1.2 基于权重的KFCM聚类算法
一般来说,KFCM聚类算法,是通过不同的核函数将数据非线性映射到高维特征空间中,使原来没有显现的特征突现出来,扩大了特征间的差异,再在高维特征空间中进行模糊C-均值聚类,能较好的实现不同数据结构的聚类[9]。但在KFCM算法中,数据之间相似度是通过欧几里得距离衡量的,特征变量对目标函数的贡献值都是相同的,而在泥石流的评价指标体系中,各指标对泥石流发育影响程度是不同的,反映到数据上面就是权重值的不同[2]。因此,本文在KFCM聚类算法的理论基础上,引入权重的概念,运用加权欧式距离来计算核函数值,如式(7)、(8),从而实现基于权重的分类。

(7)

(8)
式中:k表示表示泥石流影响因子个数,wi(i=1,2,…,k)表示各个因子的权重系数,xi表示第i个泥石流沟的评价因子,yi表示聚类中心。
经改进后的WKFCM算法计算过程如下:
(1)先初始化权重矩阵wi,隶属度矩阵U和聚类中心Vi,设置模糊参数m,高斯核函数参数σ,收敛阈值ε;
(2)运用权重矩阵wi按照式(7)、(8)计算核函数值K;
(3)按照式(5)、(6)的计算方法计算聚类中心;
(4)按照式(5)、(6)的计算方法重新计算隶属度矩阵;
(5)根据式(1)计算目标函数J,判断目标函数值J的改变量ΔJ是否小于给定的阈值ε,若小于则算法终止,否则返回步骤2继续执行。
本文将改进后的WKFCM聚类算法参照以上步骤在Matlab中进以实现,并将其应用于泥石流沟的危险性评价中。
2 基于权重的WKFCM聚类算法的应用实例
2.1 泥石流评价因子的选取
本次研究选取的是西藏境内有良好工作基础的30条冰川泥石流沟作为研究的对象,以探究基于权重的WKFCM聚类算法在泥石流危险性评价中的可行性和合理性。然乌-培龙一带是我国海洋性冰川的主要分布地区,也是我国冰川泥石流的主要集中发育地段。冰川泥石流是泥石流灾害中比较特殊的一类,冰川泥石流的危险性的评价不仅可以反映出流域的侵蚀强度,还可以反映流域内泥石流的危害性,对区域内的防灾减灾工作具有重要指导意义。
由于冰川泥石流的形成不同于一般的雨洪泥石流,其水源主要由冰雪消融、冰崩和雪崩、冰川湖溃决产生的瞬间洪流,而固体物质主要来源于新老冰川运动产生的冰碛物[10],所以在评价因素的选择上也与雨洪泥石流有所不同。铁永波等人总结了国内学者对冰川泥石流的研究成果指出冰川泥石流的形成均伴随者前期的洪水(冰湖溃决或冰雪融水)过程和后期沿程的侵蚀(侧蚀及掏蚀等)过程[11]。黄伟等人运用灰色关联度法筛选出日最高温度、流域面积、一次泥石流最大冲出量、主沟长度、流域最大高差、冰川积雪面积等7个冰川泥石流的主要影响因子[12]。王磊在研究雅鲁藏布江加查-米林段冰川泥石流形成条件与活动特征时也表明该研究区内的冰川泥石流与流域面积、沟床比降、沟床堆积物等等都有着密切的联系[13]。本文依据国内学者对冰川泥石流形成机制的分析[11-14],选取流域面积F1(km2)、沟床比降F2、岩性系数F3、构造系数F4、冰川坡度F5(°)、平均坡度F6(°)、可移方量F7(×104m3)、最大淤积F8(×104m3)、冰川面积与流域面积的比值F9等9个因素作为泥石流危险性的评价指标(表1),泥石流沟的数据来源于文献[15]。

表1 泥石流沟评价因素一览表
2.2 评价过程
本文按照如下步骤,运用WKFCM算法进行研究区内泥石流沟的危险性评价。
步骤1:先运用层次分析法计算各泥石流评价因子的权重系数,并进行一致性检验。对数据进行归一化处理以消除不同评价因子计量单位量纲之间的差异,按照式(9)计算各泥石流沟的综合加权值。
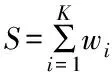
(9)
式中:S表示综合加权值,取值在0~1之间,Fi表示第i个评价因子归一化后的值,wi表示各因子对应的权重值。
步骤2:用步骤1中计算的权重系数初始化WKFCM算法的权重值,在Matlab软件中进行泥石流沟的归类。
步骤3:计算每个类别泥石流沟的综合加权值,按照从高到低的顺序赋予不同的危险度,从而实现研究区内的泥石流危险性评价。
2.3 权重计算
权重的确定方法比较多,层次分析法是因子权重确定中比较常用的方法,最早由美国运筹学家T.L.Saaty提出[16],其方法是按一定的规则对因子两两之间进行比较并赋值,构造判断矩阵,并采用随机一致性指标作数据一致性检验,若通过一致性检验,则可以得到可信度较高的计算结果。这种方法既考虑了主观不确定性因素,也结合逻辑思维定定量进行分析,是定性与定量的结合,主观与客观相结合的方法。本文采用层次分析法计算各影响因子权重。

2.4 泥石流危险性评价
根据表1中的泥石流基础数据,分别运用WKFCM算法和KFCM算法对泥石流沟进行聚类以便对比分析,两个算法都迭代计算10次后结束,将泥石流沟分为5类,求取各类别的平均综合加权值,依据各类别的平均综合加权值的高低,分别赋值为极度危险、高度危险、中度危险、低度危险和极低危险(表4)。
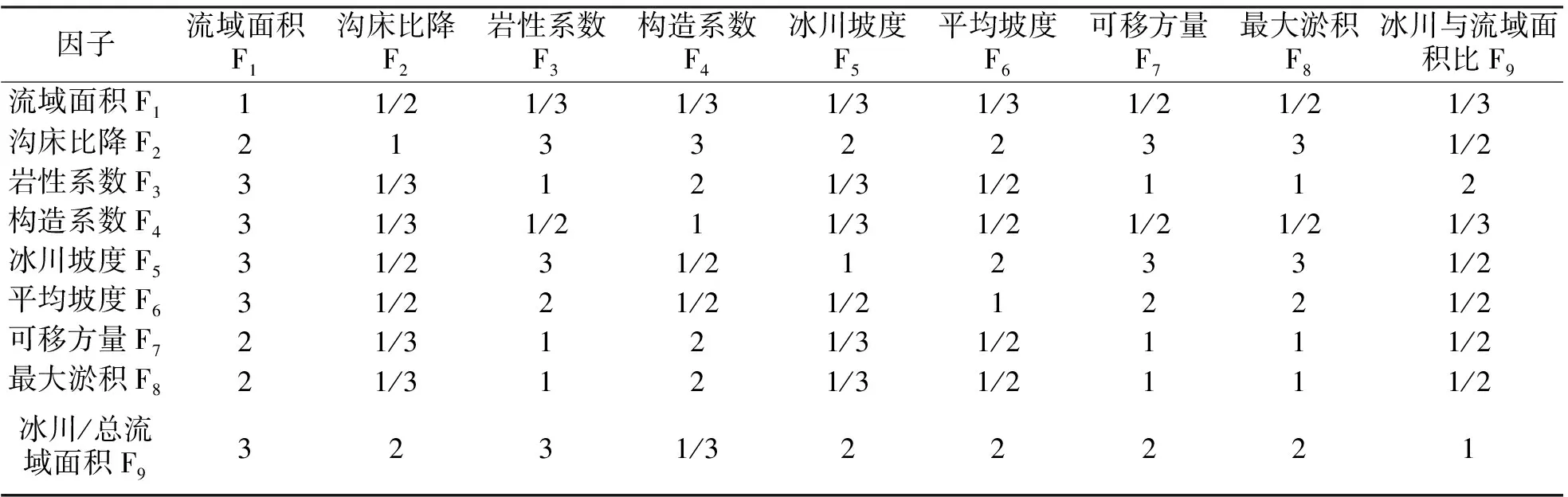
表2 判断矩阵

表3 评价因子的权重值

表4 泥石流沟危险性评价结果
3 结论与讨论
文献[15]中把区域内的冰川泥石流的活动性划分为极强、强、活跃、弱、极弱5个等级,本文评价结果把泥石流危险性划分为极度危险、高度危险、中度危险、低度危险、极低危险5个危险级别与泥石流的活动性相对应。从表4的评价结果可以看到,基于权重的WKFCM方法的评价结果,除了米堆弄巴、格曲、次浪三条沟的评价结果与文献[15]中的活动性相差较大外,其余的27条泥石流沟的评价结果与活动性强度总体上是比较一致的,吻合度达到90%;而KFCM算法的评价结果中差普、嘎浪、次浪、塞龙卡区、索通沟、角弄弄巴、卡贡弄巴、米堆弄巴、格曲等一共9个泥石流沟都与文献[15]中的活动性相差较大,吻合度只有70%,所以考虑到不同因子的权重的WKFCM方法评价精度优于普通的KFCM聚类方法。从泥石流沟的实际活动特征来看,以区域内两条著名的冰川泥石流沟培龙贡支和卡贡弄巴为例。培龙贡支曾于1983年7月28-29日、1985年5月29日暴发大型泥石流;卡贡弄巴于1950年、1953年、1954年、1972年都曾发生破坏性巨大的大型泥石流[14],活动比较剧烈。两者WKFCM方法评价的结果都是极度危险,评价的结果较为准确可靠。
WKFCM聚类算法是在普通模糊C-均值聚类的基础上改进形成的,运用高斯核函数扩大了特征间的差异,增强了分类的精度,考虑到不同影响因子对泥石流的贡献程度不同,引入了权重的概念,更加切合了泥石流的特点。整个评价过程无需训练样本,可以避免赋予分类阈值时的主观的不确定性,评价结果比较准确,可以为泥石流危险性评价提供一个新的思路。但由于目前研究条件的限制,在运用该方法时还有许多需要改进的地方,比如对于泥石流评价因子的分析上还可以进一步深入,因子选取时没有考虑到不同因子之间是否存在线性相关等等问题,有待进一步完善。
[1] 孙绍骋. 灾害评估研究内容与方法探讨[J]. 地理科学进展,2001,20(2):122-130.
[2] 王欢,丁明涛,陈廷方. 基于GIS的三江并流区泥石流危险性评价[J]. 水土保持通报,2011,31(5):167-170,267.
[3] 宁娜,马金珠,张鹏,齐识,田黎明. 基于GIS和信息量法的甘肃南部白龙江流域泥石流灾害危险性评价[J]. 资源科学,2013,35(4):892-899.
[4] 李阔,唐川.泥石流危险性评价研究进展[J]. 灾害学,2007,22(1):106-111.
[5] 王建国,杨德明,陶景梅. 基于GIS及聚类分析法的抚顺地区地质灾害综合评价[J].世界地质,2011,30(2):270-276.
[6] 桂蕾,殷坤龙,王佳佳. 基于聚类分析的滑坡灾害危险性区划研究[J]. 水文地质工程地质,2013,40(1):100-105.
[7] 丁明涛,韦方强,王欢,等. 基于聚类分析的三江并流区泥石流危险性评价[J].资源科学,2012,34(7):1257-1265
[8] 曲福恒,马驷良,胡雅.一种基于核的模糊聚类算法[J].吉林大学学报:理学版,2008,46(6): 1137-1141.
[9] 施浩琴,周德云,张堃. 基于改进KFCM聚类的数据关联算法[J].电光与控制,2012,19(4):13-17,58.
[10]张瑞江.青藏高原冰川演变与地质灾害[J].国土资源遥感,2010,86(Supp.1):54-58.
[11]铁永波,李宗亮. 冰川泥石流形成机理研究进展[J].水科学进展,2010,21(6):861-866.
[12]黄伟,唐川,刘洋. 基于灰色关联度的冰川泥石流危险性评价因子分析[J]. 灾害学,2013,28(2):172-176.
[13]王磊. 雅鲁藏布江加查—米林段冰川泥石流形成条件与活动特征研究[D].成都:成都理工大学,2011.
[14]中国科学院·水利部成都山地灾害与环境研究所,西藏自治区交通厅科学研究所.西藏泥石流与环境[M].成都:成都科技大学出版社,1999:29-39.
[15]陈杰,崔鹏,韦方强,等. 基于模糊关系理论的冰川泥石流活动性评价方法[J]. 水土保持究,2003,10(2):1-4,43.
[16]Saaty T L.The Analytical Hierarchy Process.NewYork,NY: M cGraw-Hill,1980.
Application of WKFCM Algorithm Based on Weight in Debris Flow Evaluation
Li Xuan1,2, Fan Jianrong1and Zhang Jianqiang1
(1.InstituteofMountainHazardsandEnvironment,ChineseAcademyofSciences&MinistryofWaterConservancy,Chengdu610041,China; 2.UniversityofChineseAcademyofSciences,Beijing100049,China)
Theformationofdebrisflowincludeterraincondition,geologicalstructure,weatherandotherfactors.Therearesomedifferencesandsimilaritiesindebrisflowofdifferentarea.Usingclusteranalysiscanidentifythesimilarity.GeneralKFCMAlgorithmhasalmostnoconsiderationforthecontributionofdifferentfactorshavedifferentweights,therefore,thisarticletrytoimprovetheKFCMalgorithmthroughintroducingconceptofweight,thenwegetWKFCMalgorithm.Afteranalyzethepresentdataoftheseglacierdebrisflowgullies, 9factorsarechosenasmainfactorsforevaluatingtheriskofthesegullies.AnalyticHierarchyProcessisusedtodeterminetheweightsofthefactors.ThestudyareaisslocatedinTibetalongtheSichuan-Tibethighwaywhere30glacierdebrisflowgulliesareselectedforstudy.Accordingwiththereferenceresult,itshowsthatitispracticaltousethismethodtoevaluatetheriskofdebrisflow.
weight;WKFCMalgorithm;debrisflowdisaster;evaluation
2014-12-04
2015-01-19
中国科学院科技服务网络计划项目(KFJ-EW-STS-094);数字制图与国土信息应用工程国家测绘地理信息局重点实验室开放基金(DM2013SC01);中国科学院重点部署项目(KZZD-EW-08-01)
李炫(1991-),男,四川泸州人,硕士研究生,从事地理信息系统及灾害遥感研究. E-mail: xuan121356@163.com
范建容(1969-),女,四川井研人,博士,研究员,从事山地生态与灾害遥感研究. E-mail: fjrong@imde.ac.cn
P642.23;X43
A
1000-811X(2015)03-0214-05
10.3969/j.issn.1000-811X.2015.03.039
李炫,范建容,张建强. 基于权重的WKFCM聚类算法在泥石流评价中的应用[J].灾害学, 2015,30(3):214-218. [Li Xuan, Fan Jianrong and Zhang Jianqiang. Application of WKFCM Algorithm based on weight in debris flow evaluation [J].Journal of Catastrophology, 2015,30(3):214-218.]

