高效的社会网络传递性MapReduce并行计算方法*
李国庆, 程林凤
(1.中国矿业大学 理学院,江苏 徐州 221008;2.江苏联合职业技术学院,江苏 徐州 221008)
高效的社会网络传递性MapReduce并行计算方法*
李国庆1,2*, 程林凤1
(1.中国矿业大学 理学院,江苏 徐州 221008;2.江苏联合职业技术学院,江苏 徐州 221008)
社会网络中的传递性对于网络中的社团分析和节点重要性分析都有着十分重要的意义.为了提高社会网络传递性分析中三角计数的性能,提出了一种MapReduce环境下的三角计数并行计算方法.首先,将社会网络的传递性问题转化为计算网络中三角个数的问题.其次,在计算网络中的三角时按照节点之间的度约束对重复的三角进行了过滤,并在MapReduce环境下实现了高效的三角计数并行算法.最后,分析了MapReduce环境下三角计数并行算法的时间和空间复杂性.理论分析和实验表明,该文提出的方法与相关方法相比,不仅降低了算法的内存使用量,也减小了算法的运行时间,因而更适用于大规模社会网络的传递性分析.
社会网络;三角;并行计算;聚类系数
随着“六度分割理论”的提出,社会网络引起了社会各界的广泛关注.社会网络[1]是一门与社会学、心理学、数学、计算机科学等学科相关的交差学科.社会网络分析方法将社会网络表示为矩阵,并用矩阵分析的方法分析社会网络的相关属性和特征[2].社会网络的一个重要特征是节点之间往往呈现社团结构,即社团内部节点间的连接很紧密,而不同社团节点之间的连接很松散.为了衡量节点在社团中的重要性,研究人员提出了聚类系数[3],即节点的两个不同邻居节点互为邻居的比例.聚类系数除了可以度量节点在社团中的重要性之外,还可以度量网络的传递性[4],进行异常检测[5]和基于社团的推荐[6]等.
网络的传递性依赖于网络中每个节点的度数及其聚类系数.通俗的聚类系数计算方法通过迭代网络中的每个节点,检测任意两个节点的连通性.该方法虽然简单,但是每个节点所需要的时间复杂度为节点度数的平方,即O(d2).由于社会网络的节点度数往往服从幂率分布,极少数度数大的节点将消耗大量的计算时间,这严重影响了算法并行执行的效率.为了提高算法的执行效率,Chiba等人[7]提出了一种优化序列算法,该算法在平面图上的时间复杂性为O(m·α(G)).为了解决图数据量大无法载入内存的问题,文献[8, 9]将图数据以流的形式进行处理,并提出了相应的近似算法.此外,文献[10~13]将网络的传递性问题转化为三角计数的问题,并进行了相关的研究工作.
近些年,随着信息技术的不断发展,催生了大量的海量数据社会网络,如WorldWideWeb、Facebook关系网络、网页的点击纪录网络、电子商务中的用户-商品网络等.这些网络通常含有数以亿计的节点和数十亿的边,整个网络规模已经严重超出了个人计算机的处理能力.MapReduce[14]环境应用大量的商业计算机通过并行计算的方式对海量的数据进行分析,已经成为了数据密集型计算领域的事实标准.Hadoop[15]平台作为MapReduce的开源实现,引起了工业界和学术界的广泛关注,并取得了大量的应用实例,如Pegasus[16]和Hadi[17].
本文研究了MapReduce环境下的社会网络传递性问题.由于网络的传递性与网络中的三角个数相关,本文通过过滤掉重复三角的方法来提高算法的性能.在三角的过滤过程中,本文基于节点的度数约束,实现了高效的三角计数方法,从而提高了分析社会网络传递性的性能.
1 基于MapReduce的社会网络传递性计算
1.1 问题描述
令G=(V,E)为一个无向无权图,其中节点的个数为n=|V|,边的个数为m=|E|.节点v的邻居节点集合为N(v)={u|(u,v)∈E},v的度数dv=|N(v)|.节点v的聚类系数为两个邻居节点互为邻居的比率,可表示为如下公式:

(1)
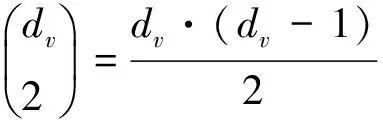
对于任意两条边(u,v)∈E和(v,w)∈E,如果(u,w)∈E,那么u,v和w构成一个三角形,这表明v此时满足传递性;如果(u,w)∉E,那么v此时不满足传递性.因而,节点的传递性等价于节点的聚类系数.
在图G=(V,E)中,对于所有的节点三元组

(2)
在公式(2)中,分子为每个节点为传递节点的三角形个数之和,值为图G中的所有三角形个数的3倍,那么公式(2)可改写为如下公式

(3)
1.2 MapReduce迭代算法
在MapReduce环境下,我们通过对每个节点进行迭代计算出每个节点的三角形个数,并将所有节点的三角形个数相加,再除以总共的三元组个数,就可以得到图的全局传递性.在计算三角形个数时,对于u,v和w构成的三角形共计算6次,其中每个节点为传递节点计算两次.如果按照节点的度数将节点排序,令dv 在应用MapReduce环境统计三角形的个数时,需要两次迭代过程.第一次迭代时,采用并行方式遍历每个节点生成相应的三元组(长度为2的路径);第二次迭代时,对每个三元组,通过扫描图中的边检查该三元组的封闭性,并对三角形进行统计.算法的细节见算法1. 算法1. 图的三角个数统计 1.Mapper1: 输入: <(u,v),∅> //图G 2.Ifdv>du 3.Emit 4.Else 5.Emit 6.Reducer1: 输入: 7.Foreach(u,w)s.t.u∈S∧w∈S∧du 8.Emit 10.If输入类型为 11.Emit<(u,w),v>; 12.If输入类型为 <(u,w),∅> 13.Emit<(u,w),-1>; 14.Reducer2: 输入: <(u,w),S> //S⊆V∪{-1} 15.If-1∈S 16.Foreachv∈S∩V 17.Emit 在第一次迭代中,Mapper1函数按照节点的度数将节点重新排序,使得度数小的节点作为键值.MapReduce环境将具有相同键值的键/值对收集起来后,作为输入发送到Reduce函数.在Reducer1函数中,由于键v小于每个值,因此值的集合S为v的邻居节点集合的子集.如果将所有Reducer1的输入数据合并起来,得到的矩阵为图G的邻接矩阵的上三角矩阵.对于每个节点v,Reducer1函数将v的邻居节点对作为值进行输出.在得到节点v为传递节点的三元组后,Mapper2函数将Reducer1的输出和原图G作为输入进行处理.在向系统存入的键值对中,-1表示该项来源于图G.在Reducer2函数中,与键(u,w)对应的值的集合S包含节点u和w的公共邻居集合以及-1.当键(u,w)的值集包含元素-1时,那么u、w及其公共邻居构成一个三角形. 在算法1中,由于限定了中心节点v的度数小于u和w的度数,并且u的度数小于w的度数,那么可以得到dv (4) 1.3 理论分析 下面对算法1的时间和空间复杂性进行理论分析. 定理1表明,在MapReduce环境中,每个机器所需要的内存都是亚线性的,因此即使图中节点的度数分布不均匀,Reducer函数也不会因数据过多而阻塞.根据定理1,可以得到如下推论. 推论1 所有Reducer1实例的输出数据之和为O(m3/2). 在含有m条边的图中,推论1为该算法的最坏情况.在实际过程中,Reducer1的实际输出数据量远远小于m3/2.在Reducer2中,对于给定的键(u,w),任何一个Reducer实例的数据量至多为O(du+dw)=O(n),因此完全可以存储在机器的内存中. 本实验采用的平台为MapReduce的开源实现平台Hadoop,编程语言为Java,实验环境为具有20个节点的虚拟机集群环境.每一个节点含有一个2.16 GHz的英特尔酷睿双核处理器,1 GB内存和500 GB磁盘存储空间,其运行的操作系统为CentOS v6.0. 实验采用的数据集为LiveJournal[18]和Tencent*http://www.kddcup2012.org/两个开放的数据集,这两个数据集均为在线社交网络数据集.LiveJournal数据集包含480万个节点和6 900万条边无向边,Tencent数据集包含1 000万个用户和300万个关注行为.在Tencent数据集中,用户间的关注关系是有向的,我们去除了边的方向,将其视为一个无向的图.在LiveJournal数据集中,平均聚类系数和三角个数是已知的,分别为0.312 3和2.8亿.Tencent数据集的聚类系数和三角是未知的. 在实验结果的性能分析中,我们将本文提出的方法与文献[9]的方法进行了对比,分别对比了算法的运行时间和内存使用量.首先,实验对比了两种算法的运行时间.在MapReduce环境下,程序的运行主要包括Map、Shuffle和Reduce三个过程,我们分别对比了两种算法在这三个阶段的运行时间.图1和图2分别为两种算法在不同数据集下的运行时间对比.从这两个图可以看出,两种方法在两个数据集下有着相似的实验结果.在Map阶段,本文提出的方法在Mapper函数中引入了两次图的输入,与此同时,Reducer1阶段的输出量减少了,总的输入数据量有少量的增加,因而算法在Mapper阶段的运行时间有少量的增加.在Shuffler和Reducer阶段,由于本文采用节点的度数来约束三角的计数方法,过滤掉了那些重复的三角,因而算法在这两个阶段的运行时间明显较少. 接下来,实验对比了两种方法的内存使用量.在MapReduce环境下,Map阶段用于逐行读取数据信息,因而其内存占用很小.MapReduce算法的内存消耗量最大的阶段为Reduce阶段对具有相同键的值集进行处理.在本文提出的算法中,内存消耗量最大的阶段为Reduce2函数.我们对比了本文提出的算法在Reduce2函数中的内存使用量和文献[9]中的Reduce阶段的内存使用量,实验结果如图3所示.从该图可以看出,在Twitter和LiveJournal两个数据集下,本文提出的方法的内存使用量都明显小于文献[9].这表明,本文提出的方法占用相对较小的内存,因而在相同的硬件环境下可以处理更大的数据集. 最后,实验对比了两种算法在Reduce阶段算法的运行时间随着节点度数的变化.在MapReduce环境下,算法的Shuffle时间由系统控制,用户通过Mapper和Reducer函数控制算法的运行.Mapper函数主要用于数据的读取预处理,因而算法的运行时间主要由Reducer函数所决定.由于实验结果在Tencent和LiveJournal数据集上的结果相似,我们只展示了LiveJournal数据集的实验结果,见图4.当针对每个节点计算其聚类系数时,随着节点度数的增大,其邻居节点增多,因而邻居节点对也增多,故Reducer阶段的运行时间逐渐增大.在文献[9]提出的方法下,Reducer阶段的运行时间近似呈指数增长,而在本文提出的方法中,Reducer阶段的运行时间近似呈线性增长. 综上所述,由于本文提出的方法在三角计数上对节点的度数进行了约束,过滤掉了那些重复出现的三角,算法在Shuffle阶段无重复出现的三角,因而在Reducer阶段的数据量大大减少了.这不仅降低了算法的内存使用量,也减小了算法的运行时间. 社会网络的传递性研究是社会网络领域的重要研究内容,它可以为分析社会网络中的社团和节点的重要性提供依据.本文将社会网络的传递性研究转化为网络中的三角计数问题.由于社会网络的规模不断增长,本文采用当前流行的并行计算环境MapReduce对三角计算进行了分析,提出了一种MapReduce环境下的并行三角计数方法.在将社会网络的传递性问题转化为三角计数的问题后,提出了一种基于节点度数约束的三角过滤方法及相应的MapReduce实现算法,并对算法的性能进行了理论分析.理论分析和实验表明,本文提出的方法与相关方法相比,不仅降低了算法的内存使用量,也减小了算法的运行时间. [1] 赵蓉英, 王静. 社会网络分析 (SNA) 研究热点与前沿的可视化分析[J]. 图书情报知识, 2011 (1): 88-94. [2] BURT R S, KILDUFF M, TASSELLI S. Social network analysis: foundations and frontiers on advantage[J]. Annual Review of Psychology, 2013, 64: 527-547. [3] EGGEMANN N, NOBLE S D. The clustering coefficient of a scale-free random graph[J]. Discrete Applied Mathematics, 2011, 159(10): 953-965. [4] REGENWETTER M, DANNA J, DAVIS-STOBER C P. Transitivity of preferences[J]. Psychological Review, 2011, 118(1): 42. [5] CAMACHO J, MACIA-FERNANDEZ G, DIAZ-VERDEJO J, et al. Tackling the Big Data 4 vs for anomaly detection[C]// Computer Communications Workshops (INFOCOM WKSHPS), 2014 IEEE Conference on IEEE, 2014: 500-505. [6] 陈克寒, 韩盼盼, 吴健. 基于用户聚类的异构社交网络推荐算法 [J]. 计算机学报, 2013, 36(2): 349-359. [7] CHIBA N, NISHIZEKI T. Arboricity and subgraph listing algorithms[J]. SIAM Journal on Computing, 1985, 14(1): 210-223. [8] COPPERSMITH D, KUMAR R. An improved data stream algorithm for frequency moments[C]// Proceedings of the fifteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 2004: 151-156. [9] BURIOL L S, FRAHLING G, LEONARDI S, et al. Counting triangles in data streams[C]// Proceedings of the twenty-fifth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. ACM, 2006: 253-262. [10] LOUCH H. Personal network integration: transitivity and homophily in strong-tie relations[J]. Social Networks, 2000, 22(1): 45-64. [11] BURDA Z, JURKIEWICZ J, KRZYWICKI A. Network transitivity and matrix models[J]. Physical Review E, 2004, 69(2): 026 106. [12] BATJARGAL B. Network triads: transitivity, referral and venture capital decisions in China and Russia[J]. Journal of International Business Studies, 2007, 38(6): 998-1 012. [13] BERRY M W, CHARTIER T P, HUTSON K R, et al. Identifying influential edges in a directed network: big events, upsets and non-transitivity[J]. Journal of Complex Networks, 2013,2(2):87-109. [14] DEAN J, GHEMAWAT S. MapReduce: simplified data processing on large clusters[J]. Communications of the ACM, 2008, 51(1): 107-113. [15] BHANDARKAR M. Hadoop: a view from the trenches[C]// Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2013: 1 138. [16] DEELMAN E, SINGH G, SU M H, et al. Pegasus: A framework for mapping complex scientific workflows onto distributed systems[J]. Scientific Programming, 2005, 13(3): 219-237. [17] TSOURAKAKIS C, APPEL A P, FALOUTSOS C, et al. HADI: Fast diameter estimation and mining in massive graphs with Hadoop[M]. Carnegie Mellon University, School of Computer Science, Machine Learning Department, 2008. [18] LAUW H W, SHAFER J C, AGRAWAL R, et al. Homophily in the digital world: a live journal case study[J]. IEEE Internet Computing, 2010, 14(2): 15-23. 责任编辑:龙顺潮 Efficient Transitivity Computing of Social Networks in MapReduce LIGuo-qing1,2*,CHENGLin-feng1 (1.College of Science,China University of Mining and Technology,Xuzhou 221008;2.Jiangsu Union Technical Institute,Xuzhou 221008 China) Research on transitivity of social networks is very important for analysis of community and node importance in social networks. In order to improve the performance of triangle counting for analyzing network transitivity, this paper proposed a parallel triangle counting algorithm in MapReduce environment. Firstly, we transformed the problem of network transitivity into the counting of triangles in a network. Secondly, while computing triangles in a network, we removed repeated triangles according to the degree constraint of nodes in a triangle, and implemented an efficient parallel triangle counting algorithm in MapReduce. Finally, we analyzed the time and space complexity of the proposed algorithm. Theoretical analysis and the experiments show that, our proposed approach has less memory usage and execution time compared with related work, and thus is more suitable for analyzing network transitivity for large-scale social networks. social networks; triangle; parallel computing; clustering coefficient 2014-11-07 江苏省教育教学改革立项重点课题项目(苏教科院ZCZ32) 李国庆(1966— ),男,江苏 徐州人,副教授.E-mail:xzcxlgq@126.com TP311 A 1000-5900(2015)02-0102-06



2 实验分析


3 结束语

