过程教学:培养学生数学素养的有效策略

数学素养是现代社会每一个公民应该具备的基本素养,《上海市中小学数学课程标准(试行稿)》在课程理念中对数学素养有专门的描述:数学素养是人们通过数学教育以及自身的实践和认知活动,所获得的数学基础知识、基本技能、数学思想和观念,以及由此形成的数学思维品质和解决问题能力的总和。张奠宙先生认为,数学素养,应包括数学意识、问题解决、逻辑推理和信息交流这样四个部分。可见,数学素养是主体对数学的体验、感悟、反思和表现。因此,教学中,教师只有组织有效的数学活动,让学生真正经历知识的形成和运用过程,才能最终达到发展学生数学能力,形成数学素养的目的。本文结合个人的教学实践,谈谈如何在过程教学中培养学生的一些数学素养。
1.在概念形成过程中,培养学生抽象概括能力
数学概念形成的教学,一般会经历一个“现实原型的感知、概念的抽象、概念的识别与现实原型的再寻求、概念的情境运用”这样一个大致的过程。教学中,教师应注意让学生经历、体验概念的形成过程,在概念形成过程中,培养学生抽象概括能力。
【案例1】反比例函数教学片断(苏科版数学八下11.1)
师:刚才同学们用函数表达式表示实际问题中变量之间的关系.
①s=90t;②y=20x+100;③t=■;④s=3a2;
⑤a=■;⑥y=■;⑦m=-■;⑧y=-300x+80.
那么,你能将它们分类吗?
(学生先独立思考,再小组讨论)
师:有结果吗?哪位同学代表本组说一说,你打算分几类?你分类的标准是什么?
生1:第一类含分母③、⑤、⑥、⑦;第二类不含分母①、②、④、⑧;
师:还有其他分类方法吗?
生2:把上述第二类再分成两种,因此可以分为三类,第一类①、②、⑧它们都是一次函数;第二类④自变量指数为2;第三类③、⑤、⑥、⑦分母是字母。
师:函数④九年级研究,下面请同学们分组合作探究函数关系式③、⑤、⑥、⑦具有什么共同特征?
生3:③、⑤、⑥、⑦解析式的右边的代数式都是分式。
生4:它们分母中都含有字母,这4个函数都不是一次函数。
生5:这些关系式中的两个变量都是反比例关系;
生6:它们自变量的指数都是-1。
师:如何描述?你有这样的经验吗?
生7:类比一次函数的概念,它们都具有y=■的形式。
师:k是什么数?有限制条件吗?
生8:k是常数,且k≠0。
师:自变量x有没有范围呢?为什么?
生9:因为分母不能为零,所以,x≠0的实数。
师:因变量y呢?
生10:y≠0的实数。
师:还有其他发现吗?
生11:函数③、⑤、⑥、⑦变量与变量的积是定值。
师:你的发现了不起!如果让你给这类函数起个名字,你能吗?
生12:形如y=■(k是常数,且k≠0)的函数是反比例函数。
师:还能写成什么形式?
生13:xy=k(k≠0)与y=kx-1(k≠0)。
上述教学片断首先从函数概念出发,列举生活中不同类型的函数关系,然后引导学生分类,把上述函数关系分成已经学过的一次函数、即将学习的反比例函数和以后要学的二次函数,在此基础上引入反比例函数概念。这种以“知识背景-知识形成-揭示联系”为线索,来呈现学习活动材料,更能帮助学生了解反比例函数在函数中的位置,进一步理解函数的本质,明确与正比例函数的异同,有助于学生形成知识结构。老师的启发追问使学生思维逐步深入,使反比例函数的本质特征逐步得到揭示,教学难点得到突破。这一过程中教师有机地渗透了“特殊到一般”、转化、建模等数学思想,有效地培养了学生抽象概括及符号化的能力,这是对学生学习力积极地“外烁”,也是学生良好学习品质的“悄然”“内生”。
2.在定理发现的过程中,培养学生科学严谨的思维品质
定理的教学,一般会经历“情境引入、探究发现、验证证明、理解与巩固运用”的过程。让学生经历定理的探索过程、发现过程,就是让学生经历发现命题、提出猜想、推理论证进而获得定理的过程。
【案例2】苏科版九年级6.4探索两个三角形相似的条件(2)教学片断。
师:研究一个图形,一般从定义、判定、性质三个方面进行。今天我们开始研究三角形相似的条件。如何研究呢?能找到方向吗?想一想,这与以前学过的什么知识有关联?
生1:与全等三角形的判定有关联。
师:相似三角形与全等三角形的关系是什么?判断两个三角形全等的方法有哪些?
生2:全等三角形是特殊的相似三角形,判断两个三角形全等的方法有ASA,AAS,SAS,SSS,HL。
师:根据特殊与一般的关系,你认为判定两个三角形相似的条件是变多了,还是变少了?
生3:应该变少,由三个变为两个条件,因为一个条件显然不行。
师:怎么变呢?即判定全等三角形条件中的“角对应相等”“边对应相等”应作如何改变?由ASA可得到三角形相似的判定方法是什么呢?
生4:“角对应相等”不变,“边对应相等”变为“边对应成比例”,由ASA可得到三角形相似的判定方法是“两角相等的两个三角形相似”。
师:很好!但这仅仅是猜想,根据我们研究全等三角形判定的经验,接下来我们应该做什么?
生5:应该画图、观察、证明。
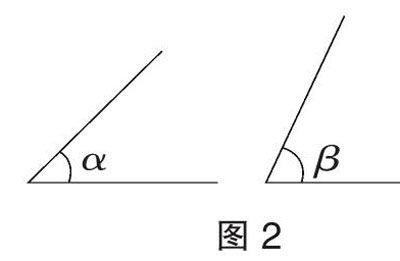
师:不错,现在同学们动手画图,如图2,已知∠α,∠β,作△ABC,使∠A=∠α,∠B=∠β。(学生动手画图,工具不限)
师:观察,同桌两人所画的两个三角形相似吗?
生(齐说):相似。
师:目前,我们证明三角形相似的方法只有预备定理,你能用学过的方法证明吗?即如图3,在△ABC与△ABC中,已知∠A=∠A,∠B=∠B。求证△ABC∽△ABC。
(学生先思考,然后四人小组讨论,再全班交流)
生6:如图4,因为∠A=∠A,平移△ABC,使点A与点A重合,AC落在AC上,AB落在AB上.又由∠ABC=∠B,可得BC∥BC,所以△ABC∽△ABC。
师:非常棒!还有不同方法吗?
生7:在△ABC边AC、AB分别截取AC=AC、AB=AB,可证△ABC全等于△ABC,并设∠ABC=∠B,所以∠ABC=∠B,所以BC∥BC,所以△ABC∽△ABC,所以△ABC∽△ABC。
师:很好!可能还有其他方法,但不管哪种方法,都离不开证△ABC全等于△ABC,以及BC∥BC。
师:这样,我们就得到这个猜想是正确的.谁能用文字语言叙述?几何语言呢?
生8:两角相等的两个三角形相似;几何语言是在△ABC与△ABC中,因为∠A=∠A,∠B=∠B,所以△ABC∽△ABC。
从以上教学片断不难看出,教师引导学生根据相似三角形与全等三角形的关系,类比全等三角形的判定方法ASA,得到猜想,再根据研究全等三角形判定的活动经验,通过画图、观察、猜想、证明、归纳得到相似三角形的判定定理1.在由猜想到证明的过程中,渗透了类比、特殊与一般、转化等数学思想,学生通过操作、观察、猜想、验证等活动,积累了基本的数学活动经验。在“猜想——论证”活动中,通过对数学的体验、感悟提升了数学素养。
3.在公式、法则推导过程中,培养学生从特殊到一般研究问题的意识
公式、法则的教学一般都要经历由特殊到一般的过程,让学生经历公式、法则的推导过程,就是通过创设合适的情境,让学生感受公式、法则学习的必要性,理解算理,理解公式、法则的合理性,能举例说明公式、法则的意义,并由此体会和感悟从特殊到一般等数学思想,进一步发展观察、归纳、类比、概括等能力,发展有条理地思考及语言表达能力,从而提高学生从特殊到一般认识问题的数学素养。
【案例3】有理数除法的教学实录片段(苏科版数学七上2.6)。
师:有理数除法怎么研究呢?之前我们有过这样的经验吗?
生1:之前我们研究过有理数的加、减、乘运算,方法是先研究几个特殊的例子,然后归纳运算法则。
师:很好!我们采取的是从特殊到一般的方法,用到了归纳的数学思想.有理数除法也采取这个方法.那应该举出几个特殊的例子呢?
生2:因为除数不能为零,所以只需要举除数与被除数取正数或负数的几个例子,比如(-14)÷7,14÷(-7),(-14)÷(-7)。
师:研究这几个算式与之前我们研究的哪种运算类似?
生3:因为加减互为逆运算,乘除互为逆运算,所以它与减法研究过程比较类似。
师:你记得如何研究14-(-7)的吗?
生3:因为-7+21=14,所以14-(-7)=21,又因为14+7=21,所以14-(-7)=14+7。
师:非常棒!这里用到转化的数学思想,把减法转化为加法.谁能类比研究(-14)÷7呢?
生4:因为7×(-2)=-14,所以(-14)÷7=-2,又因为(-14)×■=-2,所以(-14)÷7=(-14)×■。
师:很好!另外两个呢?
生5:……
师:谁能类比减法法则,得到有理数除法法则呢?
在探索有理数除法法则的过程中,不断渗透归纳、转化、分类、类比等数学思想,并站在已经学过的有理数运算基础上来研究除法,反复套用之前的特殊化、类比等研究方法。在这样的探究过程中,学生才会“身临其境”,建构起迁移能力强的知识和方法体系。
在数与式的学习中,这种类比、从特殊到一般、转化等套路会经常采用。其实在不同的知识板块中都有独自或共有的基本套路,如平面几何中四边形部分,教材编排是从一般到特殊逐步深入,每一个特殊四边形都是围绕定义、性质、判定三个方面来研究,性质与判定是通过操作、观察、猜想、证明、归纳等过程得到相关定理。教学时,利用特殊化,就能简明得到图形的定义,然后从边、角、对角线来探索图形的性质,再根据判定与性质的互逆关系,引出猜想,然后证明,得到判定定理。如果每一个特殊的四边形都按照这个套路去做,学生就会知道下一步要干什么,学生的学习就会越来越轻松。
4.在解题教学过程中,培养学生善于联想、转化、反思的良好习惯
解题教学是运用数学概念、原理,寻找问题的条件、结论,将问题转化为自己熟悉的表达方式,并连接相关知识领域通道的过程,也是一个解决问题的过程。在解题思路的获得过程中,我们需要通过学生的思维和操作活动,展现问题转化的过程,理清相关知识领域连接的通道。
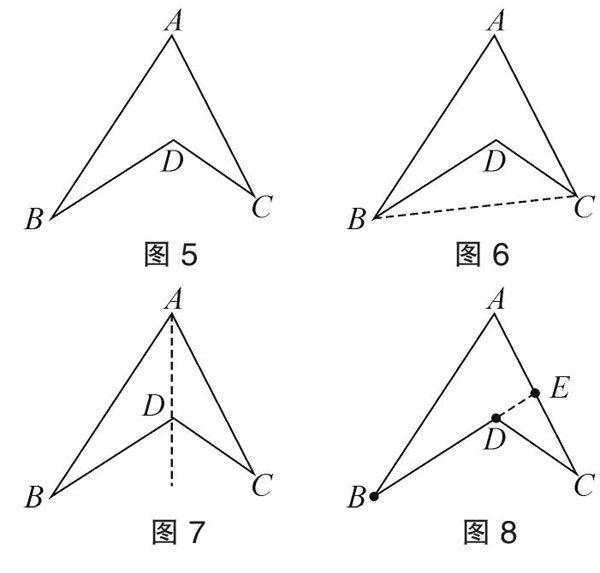
【案例4】如图5,试探究∠A、∠B、∠C、∠BDC之间的关系。
师:请同学们探究图5中∠A、∠B、∠C、∠BDC之间的关系.
生1:如图6,连接BC,用三角形内角和定理,可得∠BDC=∠A+∠B+∠C;
师:很好!还有其他证法吗?
生2:如图7,连接AD并延长到F,利用三角形外角性质,可得∠BDC=∠A+∠B+∠C;
师:对!这种证法比较简单,还有没有其他办法呢?
生3:如图8,我是延长BD交AC于E。利用三角形外角性质,可得∠BDC=∠A+∠B+∠C。
生4:我是延长CD交AB于E。利用三角形外角性质,可得∠BDC=∠A+∠B+∠C。
师:都可以。
以上是我校一位青年教师的教学片断,该片断中学生确实亲眼见到了3种证明的方法,但是,教师自始至终都只关注问题解决的结果,不追问问题解决的过程,学生也没有从该题的解题中获得应有的思维能力。作为教师,我们要从学生的经验剖析到问题的本质,应引导学生思考解题方法是怎么得到的,没有问题解决思路获得的过程,没有知识点连接的通道,学生只能被动接受,不仅不利于学生数学思维的发展,也不利于基础知识的掌握,更不要说良好认知结构的形成了。因此,在本题教学过程中,当学生说出解题方法后,教师应追问学生;“你是怎么想到这样做的?”“为什么要这样添加辅助线?”应让学生体会到辅助线的作用是把分散的条件集中,把隐含的条件显现出来,无论哪种添加辅助线的方法,都是构造新的基本图形。教师还应引导学生比较哪种方法更简洁、进一步优化学生思维结构。学生只有经历了以上的探索过程,才能知道解题思路的由来,才能提高分析及解决问题的能力,也有利于积累添加辅助线的经验,这才算真正经历了解决问题的过程。
讲题最高境界=授之方法+培之以能+强之以心。解题后需要教师有意引导学生思考问题解决的过程,自觉地总结解题过程中的活动经验;提醒学生进行问题的拓展延伸,思考问题之间的联系,从结构的高度思考问题;提醒学生思考其中蕴含的思想方法,迁移运用于其他情境等。
(赵庭标,南京东山外国语学校,211100)
责任编辑:颜莹

