基于高频方波信号注入的PMSM无传感器低速运行研究

王莉娜，郝强

（北京航空航天大学自动化科学与电气工程学院，北京 100191）

基于高频方波信号注入的PMSM无传感器低速运行研究

王莉娜，郝强

（北京航空航天大学自动化科学与电气工程学院，北京 100191）

目前，永磁同步电机（PMSM）无位置传感器运行研究受到广泛关注。采用一种基于高频方波信号注入的方法实现PMSM无位置传感器启动以及低速运行。首先详细分析了高频方波信号注入检测原理，然后对注入的高频方波信号以及电流采样模式进行了改进。向估计的两相旋转坐标系注入高频方波电压信号，根据检测到的定子电流并结合注入的电压信号即可获得转子位置，并且利用电机的磁路饱和特性，实现转子初始位置检测。所提出的改进方法不依赖于准确的电机参数，信号处理过程简单易实现。仿真结果验证了该方法的正确性。

永磁同步电机；无传感器控制；高频方波注入；Luenberger观测器

1 引言

与传统的PMSM控制策略相比，无位置传感器控制减少了机械式位置速度传感器，更能满足高可靠性、低成本以及高温高湿等恶劣环境运行等特殊要求［1］，具有良好的发展前景，因而已经成为电机控制研究领域热点之一。

目前，PMSM无速度传感器低速运行控制算法主要是基于高频信号注入检测法［2］。该方法不依赖于电机参数，适合于电机无速度传感器低速运行。传统的高频信号注入法，向电机定子绕组中注入高频正弦信号，通过检测定子电流中的高频信号成分获取转子位置信息［3］。这种方法信号处理过程复杂，对硬件电路要求较高，并且需要使用滤波器，会带来时间延迟和幅值畸变，工程实现复杂。

为了解决这一问题，文献［4］提出了用高频方波信号代替高频正弦信号注入到电机中，并给出了几种可以注入的方波类型。这种注入方法无需对高频电流响应进行解调和滤波，很大程度上简化了信号处理过程。文献［5］在文献［4］基础上，提出采样电流平均化处理方法，一定程度上改善了定子电流突变时转子位置估计误差较大的情况。但是以上文献在1个注入信号周期内只进行2次电流采样，当电机运行于转速阶跃以及负载阶跃变化等动态过程时电流变化较快，导致转子位置观测滞后，观测误差较大，影响电机运行的动态性能。

基于以上分析，本文改进注入的高频方波信号以及定子电流采样模式，提出一种新的注入、检测方法，有效提高了转子位置观测速度和精度；针对内置式PMSM采用最大转矩电流控制方式以获得最佳控制效果；并且通过该方法获得转子初始位置，以实现PMSM无传感器启动。最后在Matlab软件提供的Simulink环境下搭建仿真模型，仿真结果验证了该算法的正确性和有效性。

2 高频方波信号注入原理

PMSM在两相旋转d-q坐标系下的电压方程为

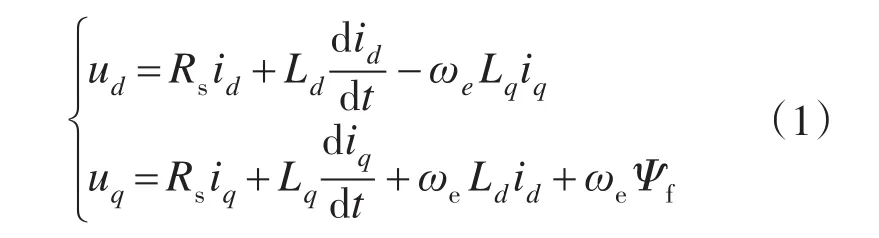
式中：ud，uq分别为d，q轴电压；id，iq分别为d，q轴电流；Rs为定子电阻；Ld，Lq分别为电机d，q轴电感；Ψf为永磁磁链；ωe为电机运行电角速度。

当注入电压信号频率远高于电机运行基波频率时，忽略该高频注入信号引起的定子电阻压降、旋转电压及反电势［6］，式（1）在高频段时可简化为

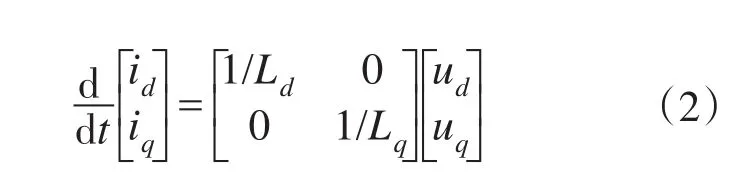
向以估计转速旋转的d′-q′坐标系中注入高频电压引起的定子高频电流响应：

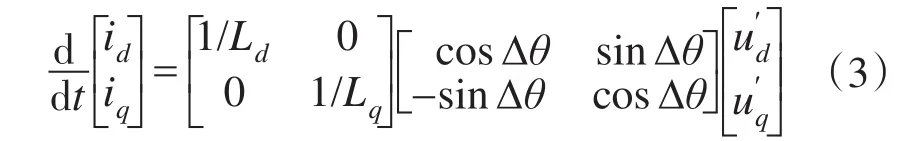
将d-q坐标系下的各量变换到两相静止α-β坐标系：

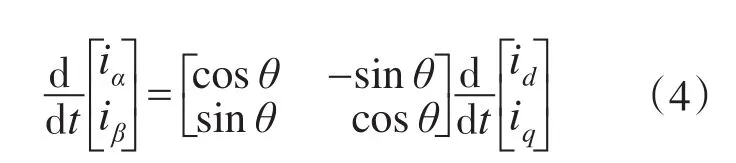
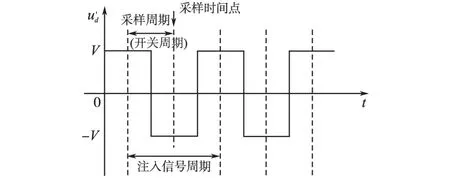
图1 注入的高频方波信号Fig.1 The high frequency square wave injected

当估计转子位置误差收敛到足够小时，即Δθ≈0，代入式（3）、式（4）可得：

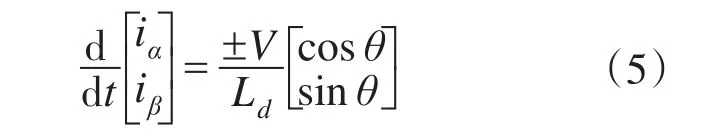
将式（5）离散化，设采样周期为T，且2次采样iα，iβ的差值分别为Δiα，Δiβ：

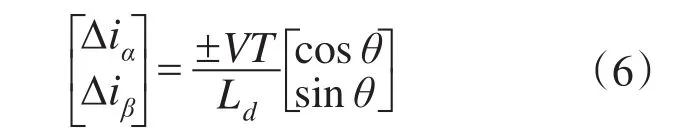
即电机转子位置信息可以根据Δiα和Δiβ获取：

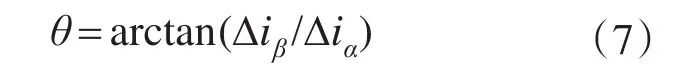
3 改进的高频方波信号注入法

在第2节分析的传统高频方波信号注入法基础上，本文改进了注入信号及电流采样模式，提高注入信号频率和电流采样频率。改进的注入高频方波信号及电流采样模式如图2所示。

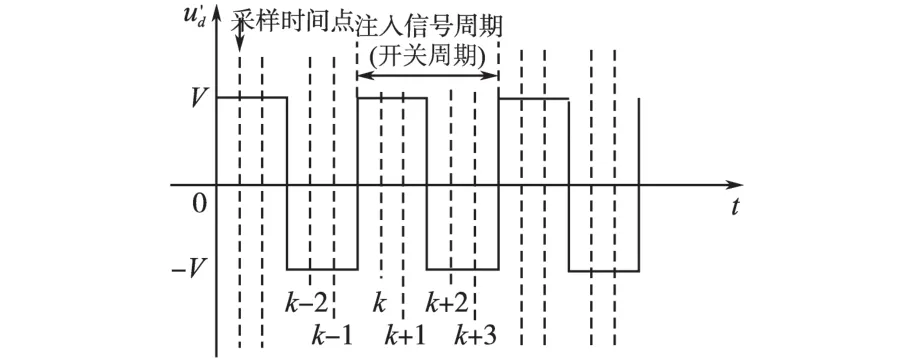
图2 改进的注入高频方波信号Fig.2 Improved high frequency square wave injected

在第k个采样时刻，定子电流增量由k时刻采样值与第k-2时刻采样值做差得到。

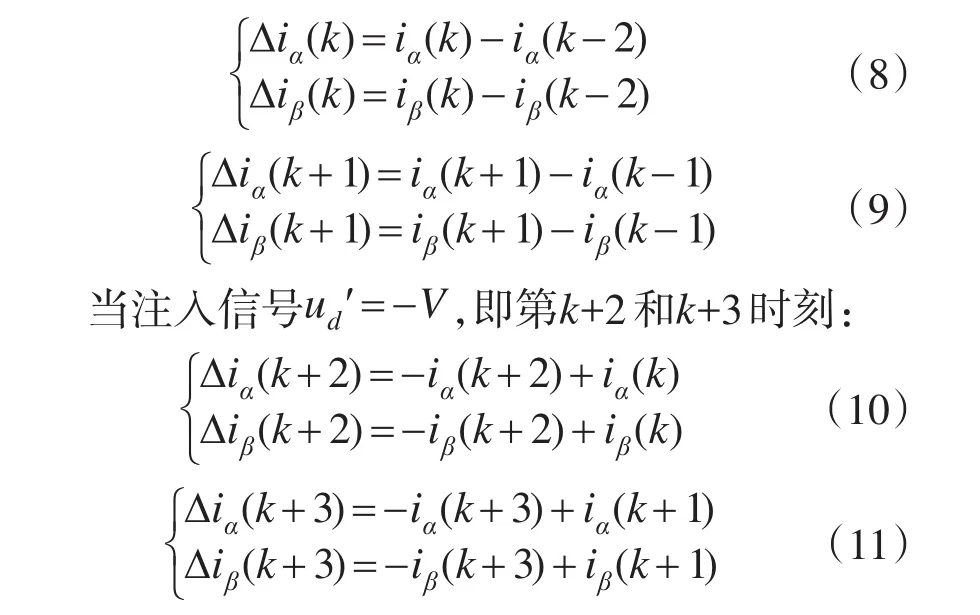
由以上式（8）~式（11）得到的定子电流增量Δiα及Δiβ，再根据式（7）即可计算得出每个采样时刻的转子位置计算值。

相比于传统高频方波信号注入法在1个注入周期内只能计算得到2个转子位置值，本文提出的改进方法能够在1个注入周期内获得4个转角计算值，加快了转子位置观测速度，能够更好地适应电机转速阶跃变化等动态过程中的转子位置估计。

由于电流采样存在一定误差和延时，直接由式（7）计算得到的转子位置波动较为剧烈，误差较大。故本文采用Luenberger观测器［7］对求反正切获得的转子位置θ进行观测，以得到平稳的转角估计值θ＾和转速估计值。

改进的高频方波信号注入法获取转子位置速度信息的基本流程如图3所示。

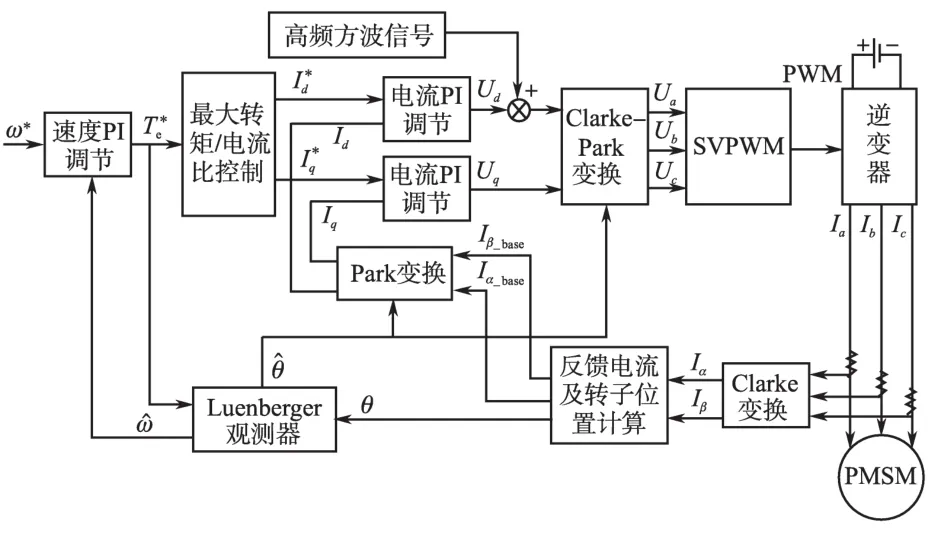
图3 高频方波信号注入法基本流程Fig.3 The flow chart of high frequency square wave injection method

4 转子初始位置检测

要实现PMSM无位置传感器控制，首先需要在无位置传感器的条件下获得较为准确的转子初始位置，以实现电机无位置传感器顺利启动。本文同样采取高频方波信号注入的方法，分两步在电机启动前进行转子初始位置辨识。首先，令控制给定信号ud=uq=0，以保证电机不运转，在此基础上向估计的d′轴注入高频方波信号，将观测器得到的转角观测值反馈至Clarke-Park变换，形成闭环调节使得式（3）中Δθ=0，即可得到转子初始角预估值θinit0，其过程如图4所示。由于内置式PMSM的凸极性是180°（电角度）对称的［8］，该θinit0可能是转子的N极与静止坐标系α轴的夹角，也可能是转子的S极与α轴的夹角，还需要进行转子极性的判断，此时可以利用电机的磁路饱和特性［9］，向预估的θinit0方向的d轴依次注入幅值为V0和-V0的电压脉冲（V0的选择应该在电机定子电流不超过额定值前提下尽量增大，以提高检测精度），这会引起定子绕组RL电路的零状态响应，较短时间后（零状态响应动态过程未结束时）检测d轴电流响应幅值，设其分别为id+和id-，如图5所示。如果id+＞id-，说明注入V0时Ld较小，注入电压增加了d轴磁路饱和，此时θinit0是转子的N极与α轴的夹角，θinit=θinit0；反之，如果id+＜id-，说明注入V0时Ld较大，注入电压减小了d轴磁路饱和，此时θinit0是转子的S极与α轴的夹角，θinit=θinit0+π。即：

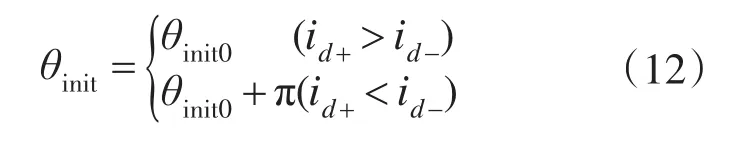
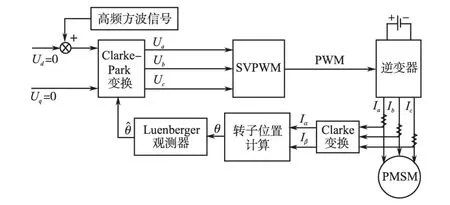
图4 转子初始角预估值判断示意图Fig.4 The diagram of rotor initial position estimation

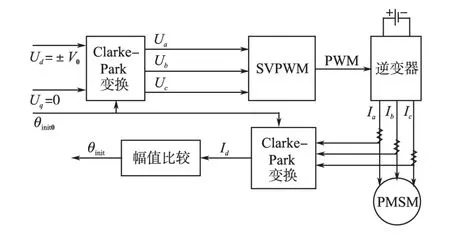
图5 转子磁极极性判断示意图Fig.5 The diagram of rotor magnetic polarity judgment

5 仿真实现与结果分析

为了验证本文算法的正确性，在Matlab软件的Simulink环境下搭建PMSM无位置传感器控制运行模型，仿真所用电机参数为：定子电阻0.331Ω，d轴电感2.1 mH，q轴电感4.1 mH，永磁磁链0.353 7 Wb，转动惯量0.025 2 kg·m2，极对数4。

基于以上电机参数，本文在电机正常运行时注入高频方波信号频率为10 kHz，幅值20 V，电流采样频率为40 kHz。

5.1 转速阶跃仿真结果

空载条件下，给定500 r/min启动电机，并于0.5 s将转速给定由500 r/min阶跃到-500 r/min，图6为观测转速与实际转速曲线；图7为电机输出转矩；图8为传统方波信号注入法（详见第2节）与本文改进的方波信号注入法观测到的转角误差；图9为以上两种方法观测的转速误差。由图6和图7可知，在转速给定阶跃瞬间观测转角转速误差较大，但随后迅速减小，给定转速阶跃0.1 s后观测转角转速以及电机输出转矩进入稳定，采用无位置传感器控制算法能够准确跟踪给定转速，实现电机正常运行，超调量小，动态效果较好。由图8可以看出，当电机稳定运行时，采用改进的方波信号注入法观测转角与实际转角误差在0.03 rad左右，明显小于采用传统的方波信号注入法时的0.06 rad；由图9可知，当电机处于转速阶跃等动态响应过程时，改进方波信号注入法得到的观测转速最大误差值比传统的方波信号注入法小20 r/min左右，说明本文改进的方法能够更好地适应电机的快速响应需求。

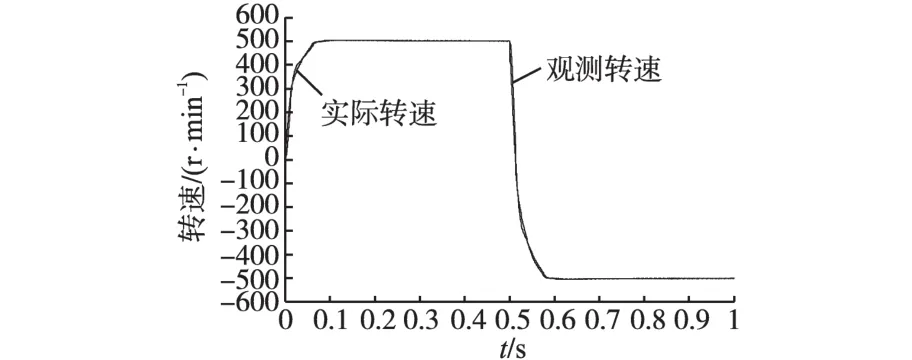
图6 转速阶跃时观测转速和实际转速Fig.6 Observed speed and actual speed at step reference speed

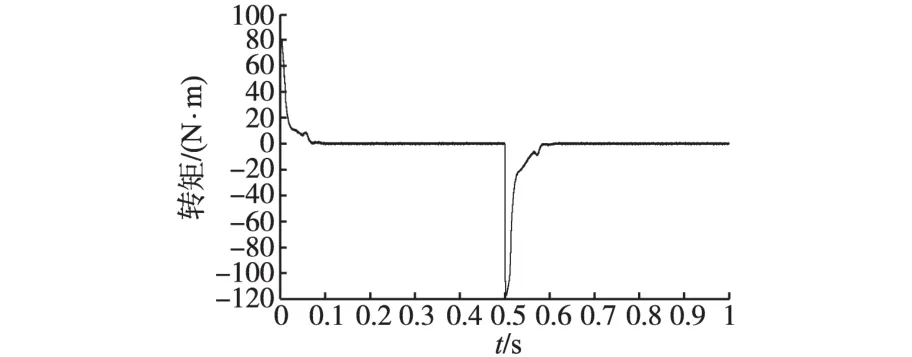
图7 转速阶跃时电机输出转矩Fig.7 Output electric torque at step reference speed

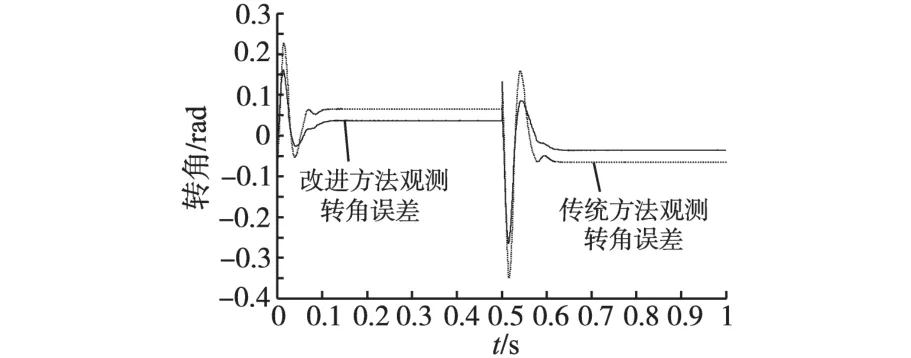
图8 转速阶跃时观测转角与实际转角误差Fig.8 Observed error of rotor position at step reference speed

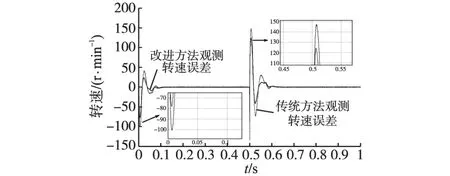
图9 转速阶跃时观测转速与实际转速误差Fig.9 Observed error of rotor speed at step reference speed

5.2 负载阶跃仿真结果

电机给定转速300 r/min，于0.2 s由空载突加15 N·m负载，0.6 s再次减为空载。图10为传统方波注入法观测转速与实际转速曲线，加减载瞬间电机转速波动40 r/min左右。图11为采用改进的方波注入法得到观测转速与实际转速曲线，加减载瞬间电机转速波动小于30 r/min，可知改进的注入观测方法有效地提高了电机无位置传感器运行时的抗负载扰动能力。图12为电机输出转矩，能够稳定跟踪负载给定，实现电机正常运行。图13为两种方法在负载阶跃过程中观测转角与电机实际转角误差，相比于传统方波注入法，改进的方波注入法在稳动态过程中观测转角误差值均有明显减小。图14为两种方法在负载阶跃过程中观测转速与电机实际转速差值，可以看出，动态过程时改进的方波注入法观测转速最大误差比传统的方波注入法小15 r/min左右。以上仿真结果及分析说明电机采用无传感器控制时，可以实现加减载正常运行，加减载引起的动态响应过程较快，系统抗负载扰动能力较强。

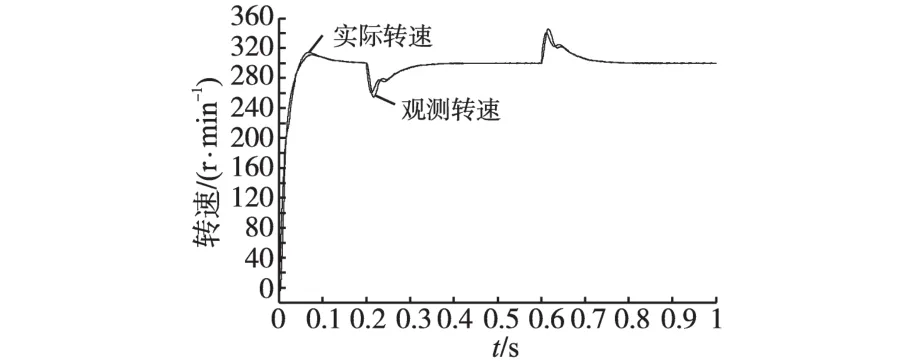
图10 传统方波注入法负载阶跃时观测转速和实际转速Fig.10 Traditional square-wave injection observed speed and actual speed at step load

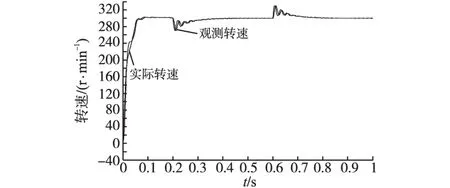
图11 改进方波注入法负载阶跃时观测转速和实际转速Fig.11 Improved square-wave injection observed speed and actual speed at step load

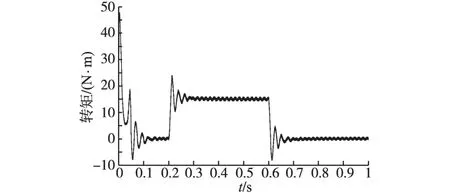
图12 负载阶跃时电机输出转矩Fig.12 Output electric torque at step load

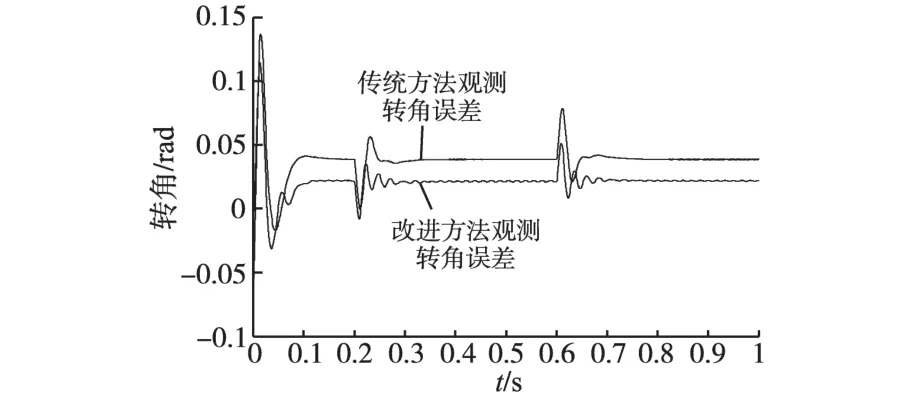
图13 负载阶跃时观测转角与实际转角误差Fig.13 Observed error of rotor position at step load

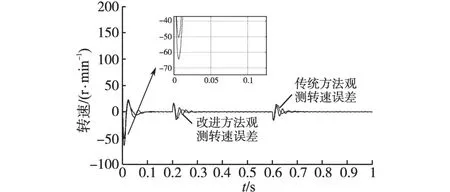
图14 负载阶跃时观测转速与实际转速误差Fig.14 Observed error of rotor speed at step load

5.3 转子初始位置检测仿真结果

由于Matlab软件中自带的PMSM模型未考虑磁路饱和，无法完成磁极极性判断的仿真。故本节根据仿真所用电机中的参数自行搭建了考虑磁路饱和的PMSM模型［10］，其中d轴电感变化范围为1~3 mH，q轴电感变化范围为2~6 mH。进行转子初始位置预估值检测时，向估计的d′轴注入幅值为±5 V，频率为10 kHz的方波电压信号，持续0.3 s；进行转子极性判断时，向d轴依次注入幅值分别为10 V和-10 V，持续时间均为0.02 s的脉冲电压信号。

图15为给定转子初始角-π/3，获得的转子初始位置预估值波形；图16为转子磁极极性判断时获得的d轴电流波形。由图15、图16可知id+＞id-，故θinit=θinit0=-1.047 5rad。

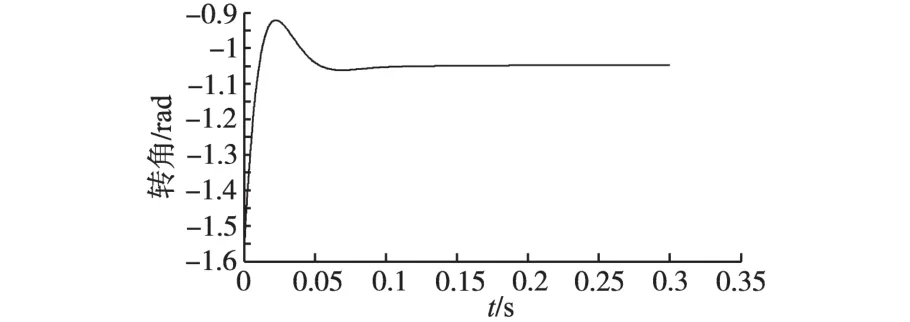
图15 给定转子初始角为-π/3时转子初始位置预估值Fig.15 Theestimatedrotorposition（theactualrotorpositionis-π/3）

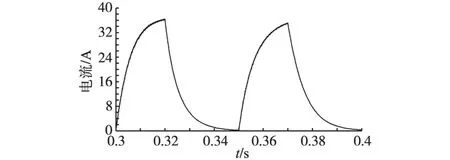
图16 给定转子初始角为-π/3时转子极性判断Fig.16 The rotor magnetic polarity judgment（the actual rotor position is-π/3）

图17为给定转子初始角π/3，获得的转子初始位置预估值波形；图18为转子磁极极性判断时获得的d轴电流波形。由图17、图18可知id+＜id-，故θinit=θinit0+π=1.047 2rad。

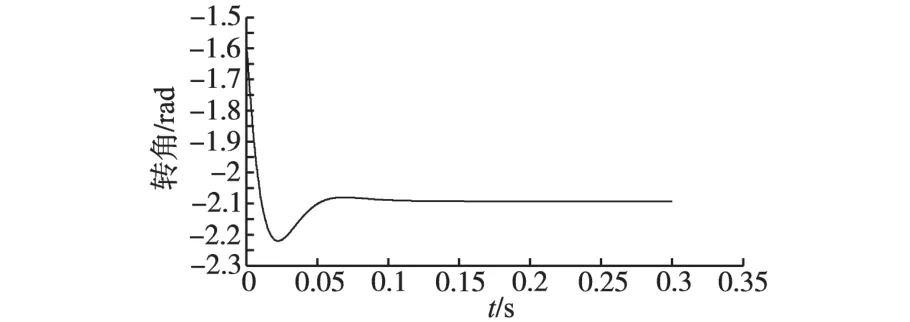
图17 给定转子初始角为π/3时转子初始位置预估值Fig.17 The estimated rotor position（the actual rotor position is π/3）

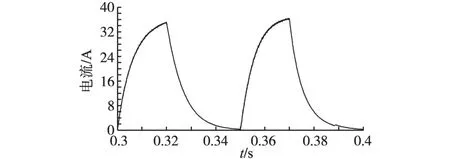
图18 给定转子初始角为π/3时转子极性判断Fig.18 The rotor magnetic polarity judgment（the actual rotor position is π/3）

图19为给定转子初始角0~2π（电角度）范围内，每隔π/6进行一次仿真，获得的观测值与实际值的差值。由图19中可以看出，观测误差没有大于0.001 rad，说明高频方波信号注入的方法能够有效进行转子初始位置检测，并且估计精度较高，可以保证电机无传感器顺利启动。

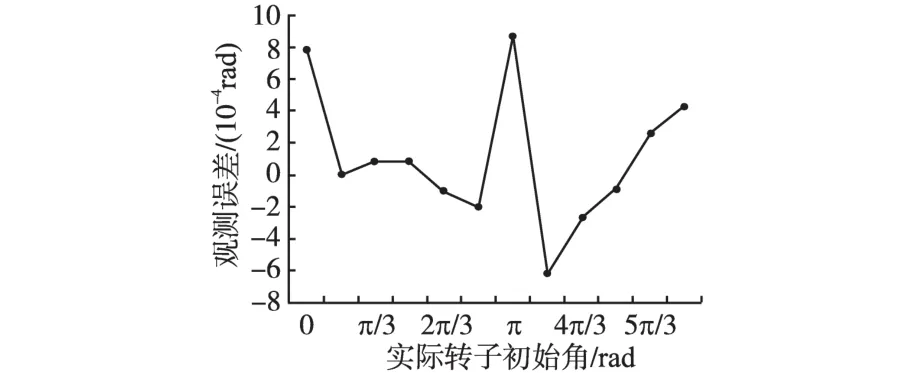
图19 0～2π范围内转子初始角观测误差Fig.19 Observed error of rotor initial position at the range of 0～2π

6 结论

针对PMSM无位置传感器低速运行，本文对传统的高频方波注入信号和电流的采样模式提出了改进，提高注入信号频率等于开关频率，并将定子电流的采样频率设置为注入信号频率的4倍，有效提高了转子位置观测速度。仿真结果表明该方法在电机匀速运行、转速阶跃变化、负载阶跃变化时均可实现对电机位置转速的有效观测，与传统的高频方波信号注入法相比观测误差有明显减小；并且该方法可以直接应用到转子初始位置检测，实现PMSM无位置传感器正常启动运行。

［1］ 王高林，于泳，李刚，等.无传感器内置式永磁同步电机低速运行转子位置鲁棒观测器［J］.中国电机工程学报，2012，32（15）：84-90.

［2］ 金光哲，徐殿国，高强，等.高频注入电压预估同步电机转子位置检测方法［J］.中国电机工程学报，2014，34（9）：1376-1383.

［3］ 王高林，杨荣峰，李刚，等.基于高频信号注入的IPMSM无位置传感器控制策略［J］.电工技术学报，2013，27（11）：62-68.

［4］ Yoon Y D，Sul S K，Morimoto S，et al.High-bandwidth Sensorless Algorithm for AC Machines Based on Square-wavetype Voltage Injection［J］.Industry Applications，IEEE Transactions on，2011，47（3）：1361-1370.

［5］ Andreescu G，Schlezinger C.Enhancement Sensorless Control System for PMSM Drives Using Square-wave Signal Injection［C］//Power Electronics Electrical Drives Automation and Motion（SPEEDAM），2010 International Symposium on.IEEE，2010：1508-1511.

［6］ 刘颖，周波，冯瑛，等.永磁同步电机低速无传感器控制及位置估计误差补偿［J］.电工技术学报，2013，27（11）：38-45.

［7］ Bimal K Bose.现代电力电子学与交流传动［M］.王聪译.北京：机械工业出版社，2005.

［8］ 李冉.永磁同步电机无位置传感器运行控制技术研究［D］.杭州：浙江大学，2012.

［9］ 万山明，吴芳，黄声华.基于高频电压信号注入的永磁同步电机转子初始位置估计［J］.中国电机工程学报，2009，28（33）：82-86.

［10］ Ichikawa S，Tomita M，Doki S，et al.Sensorless Control of Synchronous Reluctance Motors Based on Extended EMF Models Considering Magnetic Saturation with Online Parameter Identification［J］.Industry Applications，IEEE Transactions on，2006，42（5）：1264-1274.

修改稿日期：2014-12-26

Research on High Frequency Square Wave Injection Method for PMSM Sensorless Low-speed Operation

WANG Li-na，HAO Qiang
（School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Beijing100191，China）

Nowadays，the PMSM sensorless control attracts more and more attention from many researchers.A method based on high frequency square wave injection algorithm was used in the PMSM sensorless start and low-speed operation control.The principle of square wave injection method was analyzed in detail firstly.Then an improved high frequency square wave voltage was injected into the stator of the motor in the axe directions of the estimated two-phase rotating coordinate，and the stator currents were measured to extract the rotor position information with the help of the injected signal.The proposed method was independent of motor parameters and the signal processing was simple to realize.Simulation results verify the validity of the method.

permanent magnet synchronous motor（PMSM）；sensorless control；high frequency square wave inject；Luenberger observer

TM341

A

国家自然科学基金（50807002）；电力系统国家重点实验室（SKLD10KM05）

王莉娜（1977-），女，博士，副教授，硕士生导师，Email：wangln@buaa.edu.cn

2014-06-09