将探究活动进行到底——以一道试题的探究教学为例

☉江苏省淮安市淮海中学 王开林

将探究活动进行到底
——以一道试题的探究教学为例

☉江苏省淮安市淮海中学 王开林

高三数学复习课要提高课堂教学效率，教师必须精选典型例题，引导学生积极思考，合作探究，主动建构，掌握解题规律，提升分析问题、解决问题的能力，培养学生的数学思维和数学素养.为此，笔者也作了积极地探索，下面是笔者在课堂上以一道试题为引例，引导学生分析探究，总结规律，变式拓展，激活了学生的思维，点燃了学生智慧的火花，可谓精彩纷呈.

一、试题呈现

题目（金陵中学2015届高三上学期期中考试）如图1，已知椭圆别为A、B.

图1

（1）求椭圆的标准方程.

（3）在（2）的条件下，设以线段MP为直径的圆与直线BP交于点Q，试问：直线MQ是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由.

二、解法探究，寻找解题规律

解法1：设P（x0，y0），则直线AP：y=

所以直线MQ恒过点（0，0）.

评析：此解法中，以P点的坐标（x0，y0）为参变量求出点M的坐标和直线MQ的斜率，即可写出直线MQ的方程，化简得解，运算量较大.

解法2：连接BP，kOM=tan∠BOM=2tan∠BAM=2kAM.

评析：此解法中，运用数形结合得出kOM=2kAM，再结合椭圆的一个重要性质较好地减少了计算量，简便快捷多了.学生在做解析几何题时，常会出现“有思路，没结果”的现象，究其原因，主要是因为方法选择不好、运算能力不够所导致的.解法2中运用了椭圆的一个重要性质：若A、B分别是椭圆的左、右顶点，P是椭圆上异于A、B的任一点，则.此结论还可进一步推广：

2两点，P是椭圆上异于A、B的任一点，则

在解填空题时，运用此结论可以快速求解，达到小题快做的目的，解决解答题时，作为中间结论，用来突破难点，非常有效.

三、变式探究，激活数学思维

图2

小结：由探究2、3不难发现：若点D为x轴上与C点不重合的任一点，则易得kMD=tkPA（t∈R），进而可证明kDM· kPN为定值.

探究4：延长MB交椭圆于点Q，

连接AN，则AN是否经过点Q？

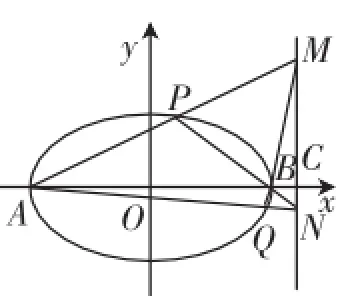
图3

所以kAQ=kAN，则AN经过点Q.

探究5：直线l的方程为x=m，是否存在实数m，使得以线段MP为直径的圆经过B点？若存在，请求出m的值；若不存在，请说明理由.

解析：假设存在，由题意知只需kBM·kBP=-1，而kAP·因此只需kBM=2kAM即可，则|CA|=2|CB|，则

探究6：记M、N两点的纵坐标分别为yM、yN，试问：yM· yN是否为定值？若是，请求出该定值；若不是，请说明理由.

探究10：以MN为直径的圆是否过定点？（以MN为直径的圆在x上截得的弦长是否为定值？）若过定点，求出定点坐标；若不过定点，请说明理由.

探究11：设以线段MP为直径的圆与直线BP交于点D，试问：直线MD是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由.

评析：以直线AM的斜率k为参数，运用直线AM与直线BP以及直线MQ的斜率的关系解题，大大减少了计算量，简便快捷，妙不可言.

探究12：连接PQ，直线PQ是否过定点？若过定点，求出定点坐标；若不过定点，请说明理由.

四、练类似题，提升应用能力

学生在经历一节课的探究之后，应该是收获很大，为了检验学生的学习效果，要求学生课后去寻找类似的题来巩固提升、体会相关的解题思路、方法与策略.

图4

类似题（泰州市2015届高三第一次模拟考试第18题）如图4，在平面直角坐标系xOy中，离心率为的左顶点为A，过原点O的直线（与坐标轴不重合）与椭圆C交于P、Q两点，直线PA、QA分别与y轴交于M、N两点.当直线PQ的斜率

（1）求椭圆C的标准方程.

（2）试问：以MN为直径的圆是否经过定点（与直线PQ的斜率无关）？请证明你的结论.

五、教学感悟

1.探究教学应凸显学生的主动建构

教育家弗赖登塔尔认为，“数学学习不是一个被动的吸收过程，而是一个以学生原有的知识和经验为基础的主动建构过程”.探究教学应突出学生的主体参与，让学生经历、实践、体验、参与、探究知识的发生、发展过程，从而激活思维，挖掘学生的潜能，培养学生学会提出问题、分析问题和解决问题.教师在课堂上起到“穿针引线”的作用，适时地启发、引导、点拨，但绝不能代替学生的思考，要充分暴露学生的思维过程，关注学生思维障碍的突破，及时纠错补错.学生只有亲历探究过程，才能获得切身的体会和感悟，才能将知识、方法内化到他已有的结构系统中，提升自己的能力.

2.变式拓展是提升解题能力的有效途径

学生为什么会陷进题海，做了一大堆的题目，成绩却进步不大？主要是老师对考点、考情、考题研究不够到位，以致于学生盲目地做题，做一些孤立的题目，高耗低效.著名数学教育家波利亚曾说过：“好问题同某种蘑菇有些相像，它们大都是成堆地生长，找到一个以后，你应当在周围找一找，很可能在附近就有好几个”.我们在高三复习课中，要学会借用波利亚的找“蘑菇”方法来探究知识与思维的“生长点.教师应该在精选例题的基础上引导学生进行变式训练，拓展探究，举一反三，触类旁通.运用变式对例题进行改编，可以改变题目的呈现方式、已知条件或位置关系，对问题进行更深层次的探索，关注结论与方法的普适性.灵活地运用变式教学，对各种题目进行归类，总结出具体的解题方法，探索解题的共性，做到深入浅出，以点带面，以少胜多，能较好地培养学生的思维能力，防止学生思维的僵化，提高学生的解题能力及应变能力，而且能激发学生学习数学的兴趣，提高学习的积极性.

3.及时反思是高效课堂的生长点

荷兰著名数学家弗赖登塔尔曾指出：“反思是数学化过程中一种重要的活动，它是数学思维活动的核心和动力”“只有这样的数学教育——以反思为核心，才能使学生真正深入到数学化过程之中，也才能抓住数学思维的内在本质”.著名数学教育家波利亚也说：“如果没有了反思，他们就错过了解题的一次重要而有效益的方面”.可见，在数学教学中，适时的教学反思对于提高教学效果是非常重要的.教学中教师还应该积极创造反思条件，强化学生的反思意识.每一次解题以后，引导学生认真地反思自己是如何发现问题和解决问题的，运用了哪些基本的解题方法和技巧，如何寻求到解决问题的思路，走过哪些弯路，从中获得哪些经验教训，也可从错误的原因反思自己是公式出错，运算出错，分类讨论出错，还是对讨论结果的整合出错，是否有更好的方法，以前是否解决过类似的问题，它们有什么区别和联系，问题的条件是否可以改变，还能得到什么结论等.学生逐步养成对自己的解题过程、思维过程进行反思的习惯，解题能力和学习效率明显提高，真正达到了事半功倍的效果.A