新旧联系促思维，小组合作放光彩——一节“正弦定理”课的启示

☉江苏省白蒲高级中学 宗新中

新旧联系促思维，小组合作放光彩
——一节“正弦定理”课的启示

☉江苏省白蒲高级中学 宗新中

正弦定理是苏教版数学（必修5）第一章“解三角形”的第一课内容，其联系起代数和几何，在高中数学教学中具有较高地位.本课是章节的起始课，是在学生具有初中解直角三角形和必修4向量知识的基础上，对任意三角形边角关系的进一步研究，定理的证明过程能为后面的余弦定理的学习埋下伏笔，具有承上启下的作用.以下是笔者本节课的教学过程和一些想法，与大家一起交流.

一、教学过程简录

1.设置情境，提出猜想

师：我们知道，生活中很多问题都可以转化为求三角形的边或角的问题，那么，任意三角形中的边角具有怎样的关系呢？不妨先来看看我们熟悉的直角三角形中的边角关系.

师：很好，很全.能将写出的边角关系归归类吗？

生：可以分为三类，正弦关系、余弦关系、正切关系.

师：根据同角三角函数关系式及诱导公式，我们知道这三种关系可以相互转化，切可以化弦，余弦可以化正弦.今天我们先来看看正弦的两个式子，它们之间有没有联系？

（学生思考片刻）

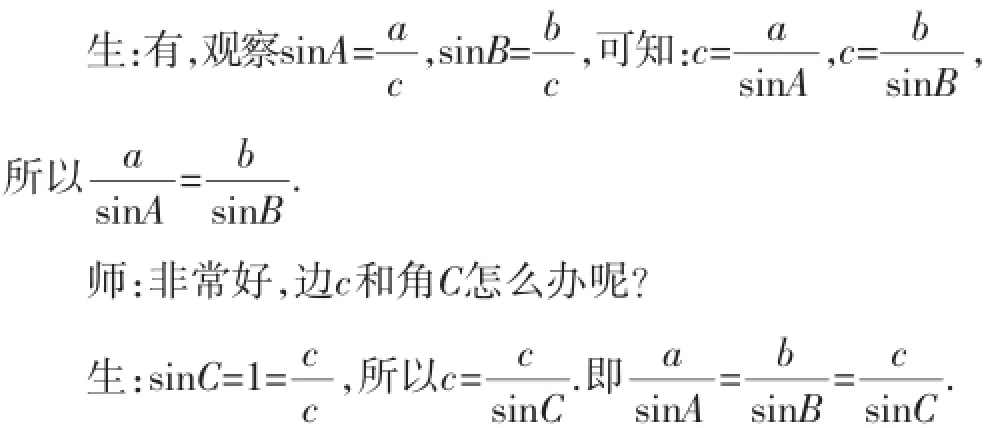
师：漂亮.这种关系在直角三角形中成立，那么它在任意三角形中成立吗？能从特殊到一般吗？

（大家议论纷纷，不约而同猜想成立）

师：很大胆，非常好，但是归纳猜想的结论不一定是正确的，需要通过严格的论证才能确保它的准确性.它究竟成立与否，我们这节课就来研究这个问题.

分析：情境设置的本质是为了提出问题，从而激发学生学习探究的欲望，其除了应该具有实用性、有效性，还应该具有连续性，也就是要着眼于学生的最近发展区，拉近初、高中的距离.利用直角三角形中的边角关系引入课题正是体现了这一点，从已知到未知符合认知规律，由特殊到一般体现数学思想.

2.探究数学，建构定理

（1）推陈出新，思维连续证明如鱼得水.

师：我们要对这个猜想作出证明，最易想到的是什么？

生：转化到直角三角形中去解决，也就是产生直角，因为直角三角形中这个结论是成立的.

师：很好，那么怎样产生直角呢？

（思索片刻，很快就有学生站起来回答）

生：我们可以通过在三角形中作高来产生直角.

师：很好，请你到黑板上来展示一下.

师：证得好，充分利用了我们熟悉的直角三角形，从一般到特殊，从陌生到熟悉，顺利得证.但是这样就证好了吗？

（好几位学生同时站起来了，争先恐后要发言）

生：刚才这位同学证得很好，但是不全面.他只是证明了在锐角三角形中结论成立.还有钝角三角形没有证明.

师：钝角三角形有什么不一样吗？

生：有，钝角三角形有两条高在三角形外.

师：很好.这位同学考虑问题很全面，现在所有形式的三角形都进行了证明，说明你们的猜想是正确的.如此简洁对称的关系式能用文字语言描述一下吗？

生：在一个三角形中，各边的长和它所对角的正弦之比相等.

师：说得好，我们就把这个优美的关系式称为正弦定理.

分析：通过构造直角三角形，把未知问题转化为已知的问题，让学生体会到了分类讨论、化归与转化、构造等数学思想，提高了学生解决问题的能力.这种方法学生容易想到，也是课本上给出的证明方法，要求学生掌握.但是这节课的精彩正是基于证明的多样性，让学生尝试从不同的角度去考虑问题，激发学生的思维，把学生的思维向更高层次推进.

（2）合作探究，思维推进火花激情四射.

师：刚才我们通过在三角形中作高的方法证明了定理，其核心思想是构造直角，还有其他的方法证明定理吗？请大家探讨一下，然后把你们的成果在小黑板上展示出来.

（学生热情高涨，分小组进行积极的讨论.学生合作探讨时，教师不能“无所作为”，要巡回查看，必要时要积极参与讨论，发现好的做法，要及时鼓励，发现好的思路而学生未能继续时要及时点拨思路.

十分钟以后，陆续有小组把思路或证明在小黑板上展示出来，并主动向大家阐述证明的思路）

组一代表：我们组发现可以用面积相等来证明.

组二代表：组一的证明是基于刚才证明基础上的，没有太多新意，我们组是利用初中的知识在圆中构造直角三角形来进行证明，因为直径所对的圆周角是直角.我们不但证明了定理并且得到正弦定理比值的几何意义即三角形的外接圆的直径.（该组只是展示证明思路，具体证明过程课后解决）组三代表：组二的想法确实比较好，但是我们的证明利用了刚学的向量这个有力的工具.

（大家明显精神一振，显然对他的说法非常感兴趣）师：你是怎么想到用向量去进行证明的呢？

生：我们组观察发现：正弦定理就是描述三角形中的长度和角度关系的，而在我们已学的知识中，向量恰好可以同时刻画长度和角度，所以就尝试利用向量去进行证明.

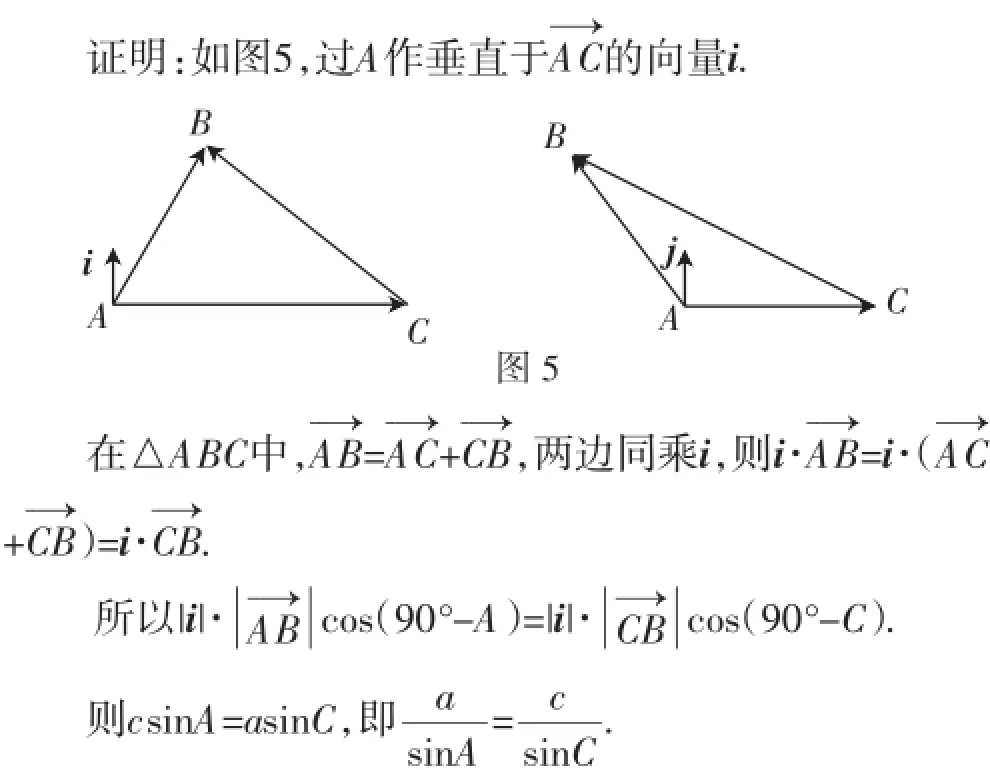
生：向量式转化为数量式的方式一是平方，二是两边同时点乘一个向量作数量积，平方之后得到的不是正弦定理的表达式，所以尝试两边同时点乘一个向量.这个向量与A→→C垂直，那么夹角就可以用A、C表示.

师：大家一起鼓掌，为精彩的证明喝彩.

分析：正弦定理的证明方法比较多，其主要思想方法就是构造直角三角形.利用圆构造直角三角形能得到正弦定理的比值的几何意义，而利用向量的方法进行证明，既展示了数与形的完美结合，也体现了向量在高中数学解题中的重要作用，同时也为后面余弦定理的证明做了铺垫.

3.简单应用，感悟定理

例1在△ABC中，已知A=30°，B=45°，a=6，解三角形.

解题过程略.

4.课堂小结，归纳提升

师：请同学们谈一谈本节课的收获和感受.

生：通过本节课的学习，我们知道了任意三角形中都有一个优美的正弦定理：

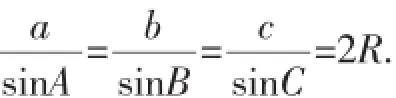
生：正弦定理的证明方法很多.

生：正弦定理的发现和推导过程中蕴含了许多的数学思想方法，如从特殊到一般、分类讨论、转化与化归等.

生：向量的作用很强大.

师：大家讲得很好.本节课我们通过自主探究，证明了正弦定理，体会了其中蕴含的数学思想方法，同时定理所展现出来的数学美也值得我们慢慢回味.

二、课后反思

1.数学课堂要体现数学的“活”

新课程标准提出数学教学是数学活动的教学.把课堂还给学生，让知识在活动中生成，让学生在活动中成长.在数学课堂中，要充分发挥出学生的主观能动性，要让每个学生都积极地参与教学活动，让学生心动起来，手动起来，嘴动起来，做课堂的主人.本节课中，教师大胆“放手”让学生自己“捣鼓”出了好几种证明方法.尤其是后面的几种解法，充分体现了合作交流的威力，让不同的思想不停地碰撞，“三个臭皮匠顶个诸葛亮”，让学生在合作交流中体验了成功的喜悦，增强了学习的兴趣.

2.数学课堂要体现数学的“美”

教学大纲中明确指出“认识数学的科学意义、文化内涵，理解和欣赏数学的美学价值”.这就要求我们在教授知识的同时，要注重渗透数学的美.本节课自始至终贯彻这一思想.课堂设计思路清晰，条理分明，不蔓不枝，体现了数学的简约美.课题的引入，情境的设置，开门见山让新、旧知识碰撞出火花，具有冲击力，能激发学生的求知欲，体现数学的连续美.同时，定理的猜想归纳体现了数学的感性之美，定理的推导证明体现了数学的理性之美，感性的归纳、理性的推导体现了数学的严谨之美，此外还有教师语言的丰富美、数学公式的和谐美（正弦定理本身就体现了数学公式的简约和谐之美），只有让学生真正地感受到了数学的美，学生才会爱上数学，才会学好数学.

3.数学课堂要让学生做到心中有“数”

根据新课程标准要求，教学要以培养学生获得终身学习能力和可持续发展的能力为终极目标.爱因斯坦也说过：“把学到的知识全部忘掉剩下的就是教育”.那么我们学生学完数学还剩下什么呢？就是要让学生在今后的学习生活中能从数学的角度去看待问题、思考问题，能建立优美的数学模型去解决问题.所以在我们平时的教学中，要着力于揭示数学结论的生成和发展过程，要带领学生体会数学现象中蕴含的数学思想方法，努力培养学生的数学思维能力，引导学生利用数学的手段去解决生活中的问题，让学生时刻做到心中有数.本节课中，注重数学思想的渗透，从一般到特殊，归纳猜想验证，分类讨论，有强烈的数学味道.A

更正证明

本刊2015年4月上高中版92页《把握知识关联问题求解自然——函数视角下数列问题的合理解答》一文的作者“江苏省丹阳市第五中学王圣光”应为“陕西师范大学江苏省丹阳市第五中学王圣光”，特此更正.