题相似法不同——由几道中考题解法谈起

☉江苏省宝应县城北初级中学 朱立业

题相似法不同
——由几道中考题解法谈起

☉江苏省宝应县城北初级中学 朱立业

最值问题是一个古老而永恒的话题，命题者的精心雕琢使近几年中考试卷涌现出一批创意新颖的试题，其中具有代表性的是“线段”型最值问题，笔者把它们归纳成几种类型，探究解决最值问题的方法，以飨读者.

一、“一动点+一定点”型

图1

例1（2012·莱芜）如图1，在△ABC中，AB=AC=5，BC=6，若点P在边AC上移动，则BP的最小值是_________.

分析及简解：点B为定点，P为动点，根据垂线段最短，当BP⊥AC时，BP有最小值.过点A作AD⊥BC于点D.因为AB=AC=5，BC=6，所以BD=3，AD=4.根据AD·BC= BP·AC，得到4×6=5BP，解得BP=，即BP的最小值是

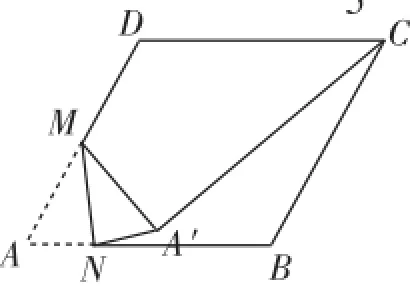
图2

【评注】应用“垂线段最短”是解决“一动点+一定点”型最基本的方法.

例2（2014·成都）如图2，在边长为2的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，则A′C的长度的最小值是______.

分析及简解：连接MC，则MA′、MC都为定值，且MC的位置确定，A′C≥MC-MA′，等号仅当点A′落在MC上时成立，此时可求出A′C的长度的最小值.

过点M作MF⊥DC于点F.

【评注】例2难度很大，直接求解无路可寻，通过构造三角形，利用“三角形两边之差小于第三边”，仅当三点共线时第三边取得最小值，这是求“一动点+一定点”型最值问题的一个重要方法.

二、“两动点”型

例3（2012·扬州）如图3，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边在AB的同侧作两个等腰直角三角形ACD和BCE，那么DE的长的最小值是__________.

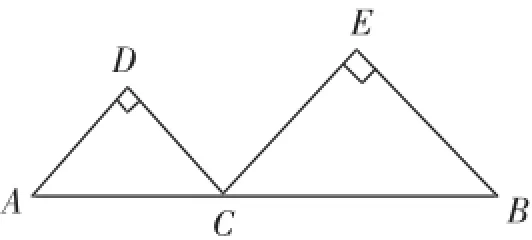
图3

分析及简解：点D、E都是动点，直接求DE的长的最小值有困难，设法转化为“一动点+一定点”型最值问题.延长AD、BE交于点G（为定点），则四边形GDCE为矩形，DE=CG，只需求出CG的最小值即可，显然，当GC⊥AB时，GC最小，且故DE的最小值为1.

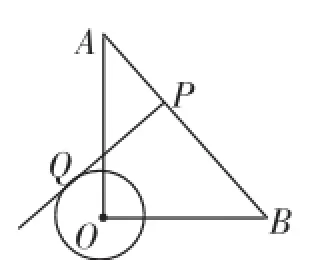
图4

例4（2013·咸宁）如图4，在Rt△AOB中，OA=OB，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为_______.

分析及简解：首先连接OP、OQ，根据勾股定理知PQ2=OP2-OQ2，O为定点，P为动点，可得当OP⊥AB时，线段OP最短，从而线段PQ最短，然后由勾股定理即可求得答案.

由PQ是⊙O的切线，得OQ⊥PQ.

根据勾股定理知PQ2=OP2-OQ2.

则当PO⊥AB时，线段PQ最短.

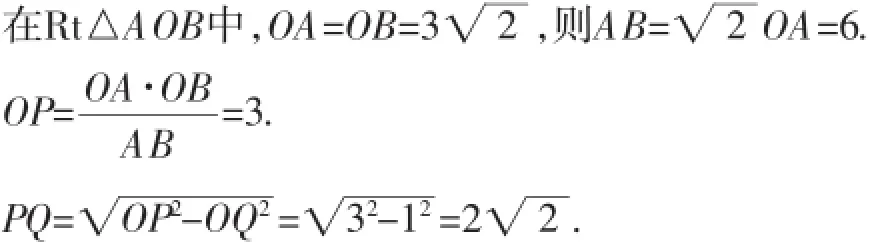
【评注】对于“两动点”型最值问题，一般可通过等量代换转化为“一动点+一定点”型最值问题，再利用“垂线段最短”求解.

三、“一动点+两定点”型

例5（2014·宿迁）如图5，正方形ABCD的边长为2，点E为边BC的中点，点P在对角线BD上移动，则PE+PC的最小值是________.

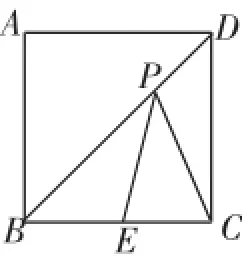
图5

分析及简解：点E、C是定点，P为动点，且E、C在BD的同侧，求PE+PC的最小值是一个基本图形与常见问题，一般用对称法求解.由点C关于BD的对称点为点A，得PE+PC=PE+AP.

根据两点之间线段最短，可得AE就是AP+PE的最小值，由正方形ABCD的边长为2，E是BC边的中点，得BE=

例6（2014·莆田）如图6，菱形ABCD的边长为4，∠BAD=120°，点E是AB的中点，点F是AC上的一动点，则EF+BF的最小值是________.

图6

分析及简解：点B、E是直线AC同侧的两个定点，点F是AC上的一动点，求EF+BF的最小值是一个基本图形与常见问题，一般用对称法求解，注意到点B与点D关于AC对称，所以连接BD、DE.根据两点之间线段最短，DE与AC的交点就是点F的位置，DE就是最小值.作DH⊥BA交AB的延长线于H.

在△ABD中，AD=AB，∠DAB=120°，则∠HAD=60°.又DH⊥AB，

【评注】“一动点+两定点”型最值问题，与课本上的一个基本图形密切相关，一般用对称法求解，是各地中考试卷最常考的最值问题.

四、“两动点+一定点”型

例7（2012·鄂州）如图7，在锐角三角形ABC中，BC=，∠ABC=45°，BD平分∠ABC，M、N分别是BD、BC上的动点，则CM+MN的最小值是________.

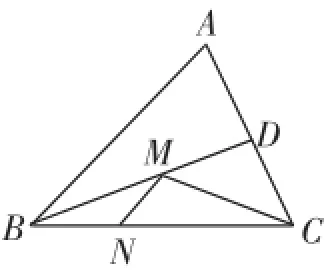
图7

分析及简解：点C是定点，而M、N都是动点，可设法`利用BD平分∠ABC，得到MN关于BD的对称线段.

在BA上截取BE=BN，连接EM.由∠ABC的平分线交AC于点D，得∠EBM=∠NBM.在△AME与△AMN中，BE=BN，∠EBM=∠NBM，BM=BM，则△BME≌△BMN（SAS），则ME=MN.

CM+MN=CM+ME≥CE.

当CE⊥AB时，CE取得最小值，从而CM+MN有最小值.

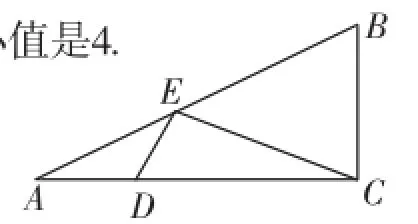
图8

例8（2014·盘锦）如图8，已知△ABC中，∠ACB=90°，AC= 20，CB=10，D、E分别是AC、AB上两点，求ED+EC的最小值.

分析及简解：点C是定点，而D、E都是动点，先设法找到CE关于AB的对称线段EG，转化为求EG+DE的最小值，这只需点G、E、D三点共线，且GD⊥AC时，GD最小，从而求得ED+EC的最小值.

作点C关于AB的对称点G，CG交AB于点M，作GH⊥AC于H，则GH就是所求的最小值.

【评注】“两动点+一定点”型最值问题难度较大，一般可先将一条线段用关于某条直线的对称线段代换，转化为“三点共线”，再利用“垂线段最短”求解.

五、“三动点”型

例9（2012·台州）如图9，菱形ABCD中，AB=2，∠A=120°，点P、Q、K分别为线段BC、CD、BD上的任意一点，则PK+QK的最小值为（）

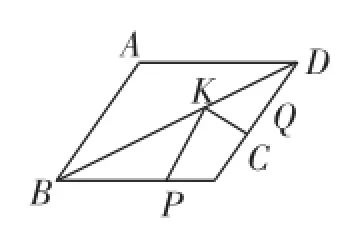
图9

分析及简解：点P、Q、K均为动点，可先作点P关于直线BD的对称点P′，连接P′K、P′Q，则P′K=PK，于是PK+ QK=P′K+QK≥P′Q，等号仅当点K落在P′Q上时成立，作QH⊥AB于H，则P′Q≥QH，即QH为所求最小值.

由四边形ABCD是菱形，得AD∥BC.又∠A=120°，则∠ABD=180°-∠A=180°-120°=60°.

例10（2014·无锡）如图10，菱形ABCD中，∠A=60°，AB= 3，⊙A、⊙B的半径分别为2和1，P、E、F分别是边CD、⊙A和⊙B上的动点，则PE+PF的最小值是________.

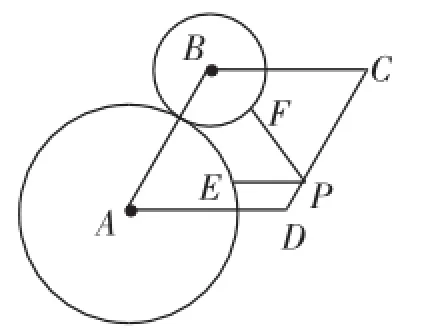
图10

分析及简解：连接BF、AE，则BF=1，AE=2，将求“PE+ PF的最小值”转化为求“PA+PB的最小值”，这就转化为“两定点+一动点”型问题.作点A关于CD的对称点A′，连接A′B，交直线CD于点P，则点P与D重合，PA+PB的最小值就是A′B的长.

易知∠BAA′=90°，∠A′=30°，所以A′B=2AB=6，即PA+PB的最小值为6，于是PE+PF的最小值为6-3=3.

【评注】例9、例10都是“三动点”型最值问题，例9是转化为“三点共线”，再利用“垂线段最短”求解；例10是转化为“三点共线”，再利用对称法求解.

感悟：波利亚说：“数学问题的解决仅仅只是一半，更重要的是解题的反思与回顾.”几何最值问题，数学课程标准未直接提及，教材中更是难见一道习题，然而，各地中考试卷却赋予了几何最值新的活力，精品试题层出不穷，有效地考查了学生分析问题和解决问题的能力.解决此类问题，需要用运动与变化的眼光去研究和观察图形，把握运动中的不变量，针对题目的特点，合理地利用“垂线段最短”“两点之间，线段最短”等原理和基本图形，将复杂问题转化为简单的常见问题，当然上述类型中的解法不是孤立的，有时一道题用几种方法求解都能奏效，而有时一道题却需要同时用几个方法才能解决，个中滋味，只有悉心体会，在解题中学习解题，才能实现解题的智慧托举.Z