从“查漏补缺”到“熟能生巧”——以“平行四边形”复习课教学为例

☉江苏省南通市第一初级中学 周红娟

从“查漏补缺”到“熟能生巧”
——以“平行四边形”复习课教学为例

☉江苏省南通市第一初级中学 周红娟

中考复习是一个老话题，各地各校都投入了很多精力研究，教师们常常都分一轮（分知识块）、二轮（分专题或题型）复习，然而一轮复习课的“范式”多是先梳理知识点（填空方式），再典型例题讲练，然后是变式训练.最近笔者有机会在南通市中考复习研讨会执教中考一轮复习课——“平行四边形”复习课，并没有采用上述“范式”教学，而是把知识梳理蕴藏到课前复习题中，开课之后就围绕相关问题对话、交流与追问，也起到了很好的教学效果.本文呈现该课的教学设计、部分教学对话，并反思复习课如何从“查漏补缺”走向“熟能生巧”，与更多同行研讨交流.

一、教学设计

（一）课前预习

题1：如图1，平行四边形ABCD的对角线AC、BD交于点O，AB＝5，AO＝3，∠ABC=50°.你能求出图中哪些线段的长和角的度数？你还能得到哪些结论？

图1

题2：如图1，四边形ABCD中，对角线AC与BD相交于点O，AB//CD.添加一个条件，使四边形ABCD是平行四边形，并说明理由.

（二）课堂学习

例1如图2，在平行四边形ABCD中，∠ABC和∠BCD的平分线交于AD边上的一点E，若___________，则AB的长是____________.（添加条件，使能求出AB的长度）

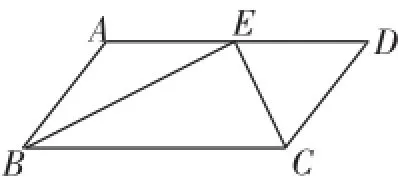
图2

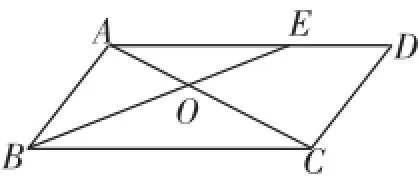
图3

例2如图3，点E是平行四边形ABCD的边AD上一点，AE∶ED＝2∶1，连接BE，和对角线AC交于点O，点O是AC的中点吗？如果是，请说明理由；如果不是，请求出AO∶OC的值.

例3如图4，已知BD垂直平分AC，∠BCD＝∠ADE，AE⊥AC，若AE=7，AB=5，AD=，求AC的长.

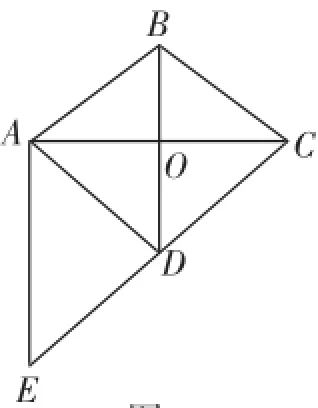
图4

图5

（三）变式生长

例3的变式如图5，以AC所在直线为x轴，BD所在直线为y轴，建立平面直角坐标系.

（1）在平面内确定点F，使以A、B、D、F为顶点的四边形是平行四边形，请写出点F的坐标；

（2）若点M在直线AD上，点N在坐标平面内，且以点B、C、M、N为顶点的四边形是平行四边形，求MN的最小值.

（四）小结与作业（略）

二、课堂生成

教学片断1（开课阶段）如下所示.

师：同学们课前已练习好了，下面我们来交流一下吧！

生1：我能得到两对全等三角形.

“不止两对”，下面马上有同学插嘴.

生1（思考了一会）：有四对，△AOB≌△COD，△AOD≌△COB，△ABD≌△CDB，△ABC≌△CDA.

师：很好.平行四边形的每一条对角线把它分成一对大的全等三角形，两条对角线相交再把它分成两对小的全等三角形.还有其他结论吗？

生2：我能求出BC边的取值范围是1＜BC＜11，对角线BD的取值范围是4＜BD＜16.

师：这位同学将平行四边形问题转化为三角形问题，其实探究了平行四边形的存在性问题，非常棒.

生3：我能得到S△ABO=S△CBO=S△COD=S△AOD.

师：很好.其中有两对三角形全等，所以面积相等，请问S△ABO=S△CBO的理由是什么呢？

生4：由平行四边形性质可得OA=OC，这两个三角形等底同高.

师：讲解思路清晰，非常好！老师在批阅大家的预习作业的时候，发现有同学还得到了∠ABD=∠CBD=25°的结论，你赞同吗？

生5：这是菱形才有的性质，平行四边形没有.

师：对！菱形才有对角线平分一组对角的性质，一般的平行四边形没有，例1也帮我们证实了这一点.

师：关于例1，大家在课前设计了一些不错的题目，但是也有些题目有点瑕疵.你能发现吗？比如有同学设计了问题：若CD=5，则AB的长是5.请你揣摩一下.

生6：他这个问题都用不到角平分线这个条件.

师：问题找出来了.你分析下出现这个问题的原因？

生6：我觉得是学习态度不够端正，应付作业.

师：我相信这样设计题目的同学自己也发现有问题，但不愿再多想，希望下次能改进.下面看另一同学的设计：若AD=13，CD=5，则AB=8.

生7：他可能是先证明得DE=CD=5，然后证明AB= AE=AD-DE=13-5=8.

师：那么问题在哪儿呢？

生7：AB和CD是平行四边形的对边，应该相等，他可能做的时候忘记用这个条件了.

师：分析得很在理.同学们基本都能看出如图2所示的基本图形，但是却忽略了平行四边形的对边相等这一条件.解决数学问题时，我们不能把条件孤立，这样常常导致题目解不出或是出错.其实这样分析下来，我们就得到很多同学设计的一类好问题：若AD=10，则AB=5.

师：还有一种设计：若∠BEC=90°，∠EBC=30°，CE= 5，则AB=5.

生8：这个和刚才的问题有类似情况，就是条件有多余.我们是可以证明∠BEC=90°的.

师：哪位同学简单证明给我们听一下？（生9）你来试试.

生9：由平行四边形得AB∥CD，所以∠ABC+∠BCD= 180°，再加上角平分线的条件，则∠EBC+∠BCE=90°，所以∠BEC=90°.

师：很好.其实这也是我们平时常常用到的基本图形，平行线截得的同旁内角的角平分线互相垂直.只需将“∠BEC=90°”这一条件去掉，就是一道好题！当然还有同学又稍作变换，设计成“若CE=3，BE=4，则AB=2.5.”这样的好问题.同学们课后可以继续探究！

教学片断2如下所示.

以下为例3的变式问题的教学对话.

师：从刚才我巡视的情况看，还有一部分同学没有将符合条件的点F都找出来.那么该如何画图确定点F呢？

生10：要分类讨论.

师：如何分？

生10：分成AB是边和对角线两类情况：如果AB是边，那么AB∥DF，可以确定两个点F；如果AB是对角线，那么AB与DF互相平分，则确定点F.

生11：在A、B、D、F四个点中，有三个顶点A、B、D都是确定的，所以我认为也可以按AB、AD、BD分别作为对角线来分类.

师：刚才我们两位同学按“两个定点”和“三个定点”两类不同问题，进行了不同的分类讨论，当然，我们也可以将“三个定点”按“两个定点”的方法进行讨论，大家的想法都很好.你能快速地写出点F的坐标吗？

（大约2分钟后，很多同学都举手了）生12：（-4，7）或（-4，-7）或（4，-1）.师：能讲一下你是如何求的吗？

生12：当AB是边时，就用坐标平移规律来求，当AB是对角线时，AB的中点也是DF的中点，可以用中点公式来求.

师：简洁而清楚.最后，我们来看例3的变式第二问.请大家先独立思考，然后在小组内交流讨论.

（大约5分钟后）

师：哪一小组先来谈谈你们的想法？

生13：我们还没求出来，只是有思路.

师：不要紧，你先谈思路.

生13：和前面的问题一样，我们分成BC是边和BC是对角线两种情形.当BC是边时，MN＝BC＝5；当BC是对角线时，如图6，设BC与MN交于点P，MN＝2MP，所以当PM最短时，MN最短.而当PM⊥AD时，PM最短.但是我们现在还没求出来.

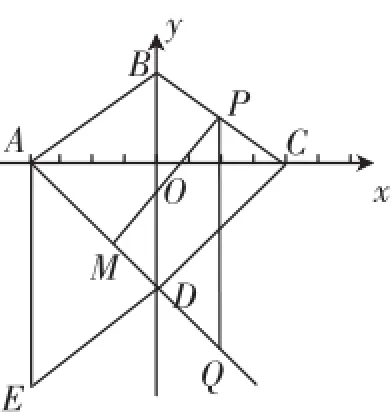
图6

师：刚才这一组同学给我们讲了他们的想法，由于时间关系，课堂上只能讨论到这里，请大家课后积极思考，将你的方法整理出来.

后记：在第二天的作业中，学生展示了几种不同解题思路.

思路1：利用PM⊥AD求出PM所在直线的解析式，再求出点M的坐标，用两点之间的距离公式求PM的长度；

思路2：发现M是直线AD：y=-x-4上一动点，设M（a，-a-4），利用两点间的距离表示出PM2，转化为二次函数的最值问题；

思路3：过P作y轴的平行线交直线AD于点Q，发现：△PMQ是等腰直角三角形，先求出PQ的长度，进而求PM的长度.

当然，还有其他大同小异的方法.

三、教后反思

上面呈现了教学流程与部分教学对话，以下再围绕该课的教学立意给出一些整体解读与思考.

1.中考一轮复习课追求查漏补缺

进入中考复习之后，师生都有着强烈的功利愿望，即希望在即将到来的中考中获得较为理想的分数，这时不能遗漏课标、教材上涉及的知识点、概念或性质.那么，在中考一轮复习中，更加侧重基础知识的覆盖与梳理，教师该怎样带领学生复习呢？是罗列知识点以填空方式给出，还是梳理成知识框图让学生填空？从上面的课例发现，我们没有这样做.而是通过前置课前预习作业，精心预设两道覆盖面较广的练习题，让学生调动自己的知识储备回顾和复习知识点，再通过开课阶段对这些问题的对话与追问，很好地起到了复习概念、梳理知识框架的作用.

2.中考一轮复习课需要熟能生巧

我们知道，当前中考试卷一般都有25～28道考题，这对解题速度有较高的追求，特别是基础题、中档题的解题速度往往决定了考生是否有更多时间投入到具有区分功能的把关题上去.那么在一轮复习中，注意训练学生的解题速度是较为现实的目标.追求熟悉题、中档题的熟能生巧，其中颇受争议的“一看就会、一做就对”也是一些应试的无奈之举.然而，究竟带给学生怎样的熟能生巧，生出什么样的“巧”，而不是熟能生厌，倒是值得研究的话题.可以发现，在上文教学片断2中，我们通过追问学生的理解，向问题的本质不断逼近，使得解法得到优化，思路得以开阔，解题途径得到开拓，这一方面追求了问题解决，另一方面也实现了我们所追求的熟能生巧.

四、写在后面

复习课是一首老歌，一方面复习内容是旧的，另一方面有些复习课的“范式”（如知识梳理、例题讲解、变式练习等）由来已久，如何追求老歌新唱，唱出新意，是我们努力追求的.当然，我们的努力还是初步的，期待批评指正.

1.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014，52（10）.

2.刘东升.关联性：一个值得重视的研究领域［J］.中学数学（下），2013（12）.

3.肖维松.熟能生巧：复习课的一种追求［J］.中学数学教学参考（中），2013（7）.

4.张奠宙.熟能生巧：是精熟，不是烂熟［J］.数学教学，2013（5）.

5.李士锜.熟能生巧吗［J］.数学教育学报，1996，5（3）.

6.李士锜.熟能生笨吗？——再谈“熟能生巧”问题［J］.数学教育学报，1999，8（3）.

7.李士锜.熟能生厌吗——三谈熟能生巧问题［J］.数学教育学报，2000，9（1）.

8.郑毓信.由“熟能生巧”到自觉学习：搞好数学教学的一个关键问题［J］.数学教育学报，1999，8（2）.Z