最优控制在吊车数控系统中的应用

张丽，朱珠

(1．江苏盐城工业职业技术学院机电工程学院，江苏盐城 224000;2．贵州理工学院电气工程学院，贵州贵阳 550001)

0 前言

随着现代生产力水平的提高，桥式起重机作为重要的搬运工具在工业生产中起到越来越重要的作用，并被广泛应用于工厂、水电站、码头以及仓库等各个领域［1］。然而，起重机在作业过程中极易引起吊重的摆动，并进一步引发安全事故。因此，为了提高桥式起重机的安全性与可靠性，提高生产效率，采用某些控制方法对其吊重摆动进行有效抑制是非常必要的［2-3］。但是，一些传统的控制方法，如极点配置方法［4-5］等，很难使起重机控制系统的性能满足现场环境的需求，因此有必要开展吊车系统控制技术的研究。

同时，目前的大多数研究中均针对连续吊车系统进行控制策略的研究［2-5］，一些复杂的连续域控制算法很难通过搭建模拟电路的方式实现，而工程应用时将其进行简单的离散化处理并不可行。然而，随着单片机和DSP的出现和发展，使得吊车系统的模块化和全数字化更容易实现，控制算法的实现经常利用数字计算机，因此很有必要在离散领域研究吊车系统控制技术。这就要求我们在离散域内研究吊车控制系统的被控对象以及相应的控制算法，这也是文中的主要出发点。

LQR(Linear Quadratic Regulator)即线性二次型调节器［6］，其对象是现代控制理论中以状态空间形式给出的线性系统，而目标函数为系统状态和控制输入的二次型函数。LQR最优设计是指设计出的状态反馈控制器要使二次型目标函数最小化，故具备良好的综合性能优势。LQR理论是现代控制理论中发展最早也最为成熟的一种状态空间设计法，特别可贵地，LQR可得到状态线性反馈的最优控制规律，易于构成闭环最优控制，因此得到了广泛的研究和应用［7-11］。此外，Matlab软件的应用为LQR理论仿真提供了条件，更为实现稳、准、快的控制目标提供了方便。正是因为LQR这些优良的控制特性和品质，因此文中将其引入到吊车数控系统的设计中。

本文作者首先利用Lagrange方程建立了吊车系统的非线性数学模型。然后对所建立的连续数学模型进行离散化处理，并基于此，应用离散LQR最优控制理论研究起重机的吊重摆动控制策略。最后通过计算机仿真验证文中控制方案相比传统控制方案的性能优势。

1 问题描述

吊车系统的整套机械部件安装在一块底板上，底板上固定着导轨、皮带轮、电机、测速机、车位置反馈电位计，底板开槽，使吊摆垂下去。吊车组件包围在轨道外，4个车轮在导轨上方运动、吊车板下面连着小车板支架和角位置电位计支架，两支架之间安装吊摆，在角位置电位计支架上装有测量吊摆角度的单圈电位计。桥式吊车控制系统的示意图如图1所示。

图1 桥式吊车控制系统示意图

图1中，M为车重，m为吊物质量，g为重力加速度，l为摆长，φ为摆角，u为伺服控制器的输出电压，x为车质心的水平位置，y表示吊物的水平位置，z表示吊物的竖直位置。

为了更加清楚地掌握单摆的运动模型，图2给出其受力分析示意图。

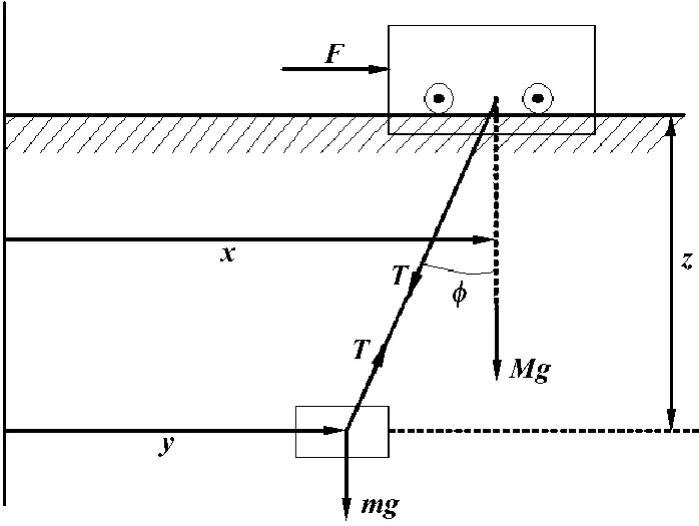
图2 单摆的受力分析图

图2中，F表示吊车的控制力，T表示货物受到的拉力。

单摆是一个两自由度系统，广义坐标为q1=x，q2=φ。系统的Lagrange函数为:

进一步可以得到:

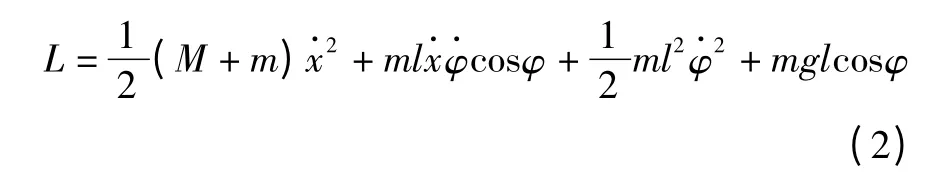
根据式(2)，可以得到Lagrange方程组为:)

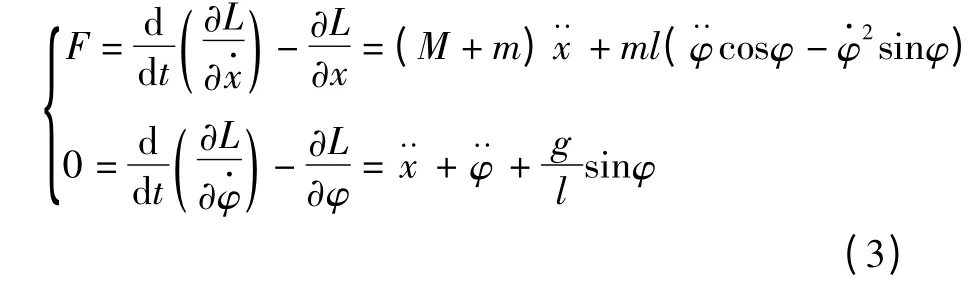
选取状态变量为xp=［xφ］T，则Lagrange方程组可变形为如下状态空间的形式:

其中，

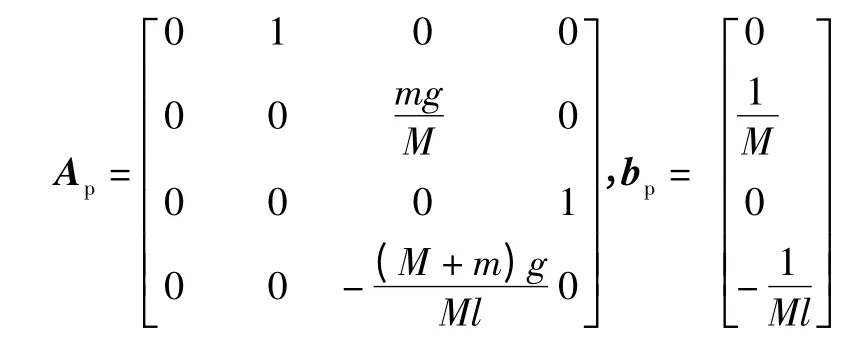
式(4)中的控制力F是由直流伺服电机提供的，并且通过精确控制直流电机可以得到期望的控制力。在忽略了感抗的影响以及启动死区电压后，可以将直流电机视为一个二阶的线性系统，其模型如图3所示。

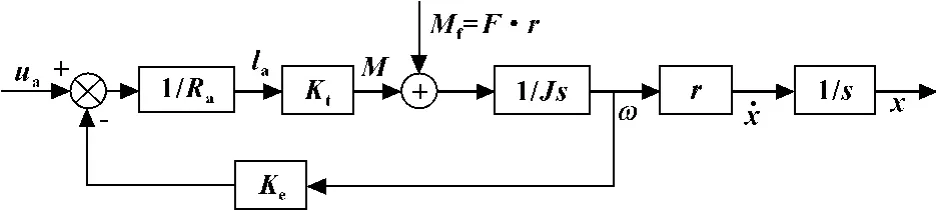
图3 直流电机的结构框图

图3中，Ra为电机的电枢电阻，Ke为电机的反电势系数，Kt为电机的力矩系数，J为电机电枢绕组的转动惯量，r为皮带轮的半径，ua为输入到电机的控制电压，Ⅰa为电枢电流，ω为电机的旋转角速度。

根据图3，可得到如下的传递方程:

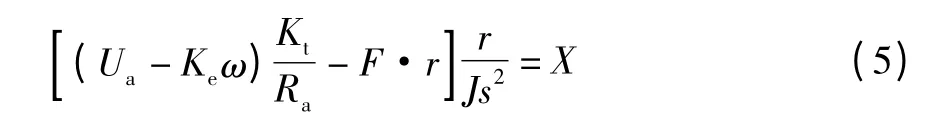
将上式写为关于时间的微分方程形式:

进一步整理可以得到:

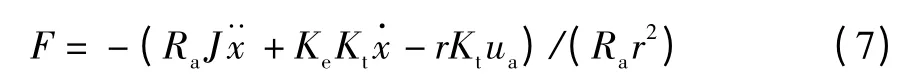
同时，考虑到功率放大器的作用，则可以得到伺服电机的输入电压ua与控制器输出电压u之间的关系:

将式(7)—(8)代入到式(4)中，可以得到平衡位置附近处电机加单摆对象的数学模型:

其中，

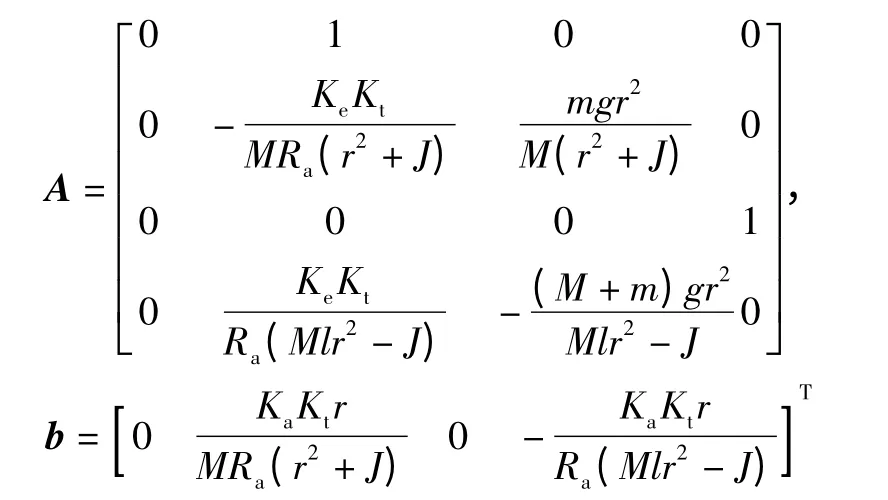
至此，吊车系统的连续状态空间方程建立完毕。于是，下一步吊车系统的控制目标是:当滑车在导轨上以一定速度和加速度运动时，应保持单摆的摆动角度最小，或单摆有任一初始摆角时，系统将使其迅速返回平衡位置。

2 离散控制方案设计

2．1 连续系统离散化

计算机控制系统与模拟控制系统的不同之处在于，在模拟系统中，信号的传送不需要数字化;而计算机系统必须先进行A/D转换，输出控制信号也必须进行D/A转换，然后才能驱动执行机构，吊车计算机控制系统的结构框图如图4所示。因为计算机有较强的计算能力，所以控制算法的实现和改变都很方便。

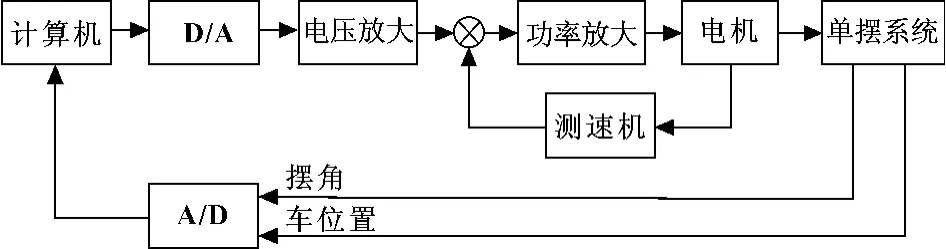
图4 吊车计算机控制系统的结构框图

由于实际的计算机控制是离散的，所以要将式(9)表示的系统离散化。若T为系统的采样周期，则可根据［19］:

得到离散化后的系统为:

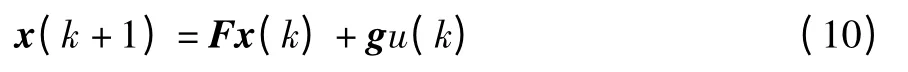
因为文中研究的吊车控制系统阶数较高，如果直接通过转换关系式(9)获得离散系统的状态矩阵F和控制向量u是很复杂的，因此我们可以借助具有强大计算功能的Matlab软件，并进一步通过函数c2d实现，其具体实现形式如下:

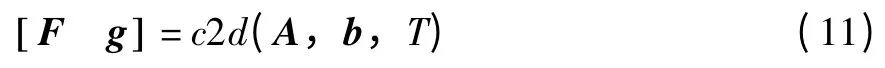
于是，下面将针对离散模型式(10)来设计吊车系统伺服电机的控制策略，该模型更符合数字控制系统的特性，具有较好的实用和工程应用价值。

2．2 离散最优LQR控制

针对2．1节建立的离散模型式(10)以及系统的控制目标，将利用最优二次型调节理论，设计吊车计算机系统的离散最优LQR控制器。

综合考虑单摆状态的收敛性以及电机的能量消耗，可以选取离散性能指标函数为:

不失一般性，Q选取为正定对称阵，且R为正数。

假设吊车数字系统式(10)是可控的，为了实现性能指标函数式(12)的最优化，根据LQR最优控制理论，可以设计如下的离散控制律:

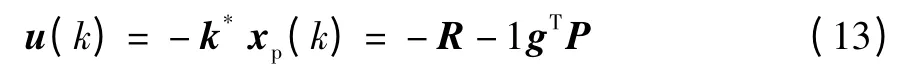
其中，k*表示最优控制增益向量，而且矩阵P满足黎卡提矩阵代数方程:

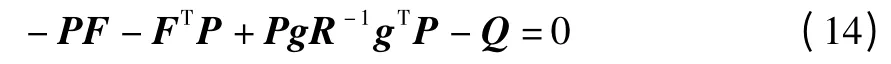
同样地，因为吊车数控系统的阶数较高，若通过求解方程式(14)来获取控制增益向量是不现实的。于是，我们仍然可以借助于Matlab计算功能，并采用函数care求取黎卡提矩阵代数方程(14)或采用函数lqr直接获得控制增益向量k*，后者的具体实现形式为:

至此，关于吊车数字系统控制器的设计完毕，下面将通过计算机仿真来验证其合理性。

3 仿真结果

仿真中，吊车系统的参数如表1所示。

表1 吊车系统的相关参数

注意，仿真时两个不能直测得的状态量(车的速度、摆的角速度)可以采用位移量或角度量差分计算。设摆角的初始角度为60°，小车的位移为-0．3 m。而且，直流力矩电机的最大控制电压为25 V，其死区电压为2 V。

将吊车系统参数值代入到状态空间方程式(9)中，可得到系统矩阵和控制向量分别为:

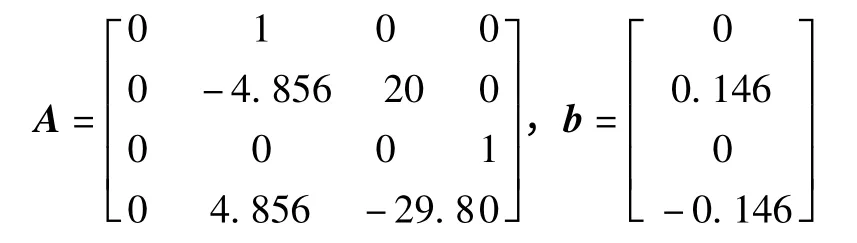
数控系统的采样周期选取为0．025 s，则根据式(11)可以得到离散化之后系统矩阵和控制向量分别为:

根据可控性矩阵ctrl(F，g)的秩等于4，可以得到离散系统式(10)是完全可控的，因此我们可以通过状态反馈实现系统极点的任意配置。

对于传统的极点配置方法:设连续域内期望的极点分别为p1，2=-1，p3，4=-2±j2，则其对应的离散域内极点为q1，2=0．975，q3，4=0．95±0．047 5j。利用Matlab的acker函数，可求得反馈增益向量为:

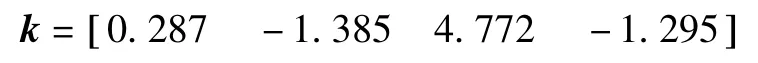
此时，给出极点配置方法下吊车系统各状态的收敛曲线，如图5所示。

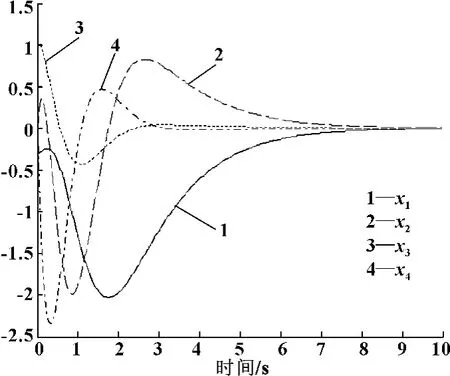
图5 极点配置方法下吊车系统的状态收敛曲线

对于离散LQR方法，首先选取二次型指标加权量为:

这时根据式(13)可以得到最优状态反馈增益向量为:

此时，吊车系统的各状态收敛曲线如图6所示。

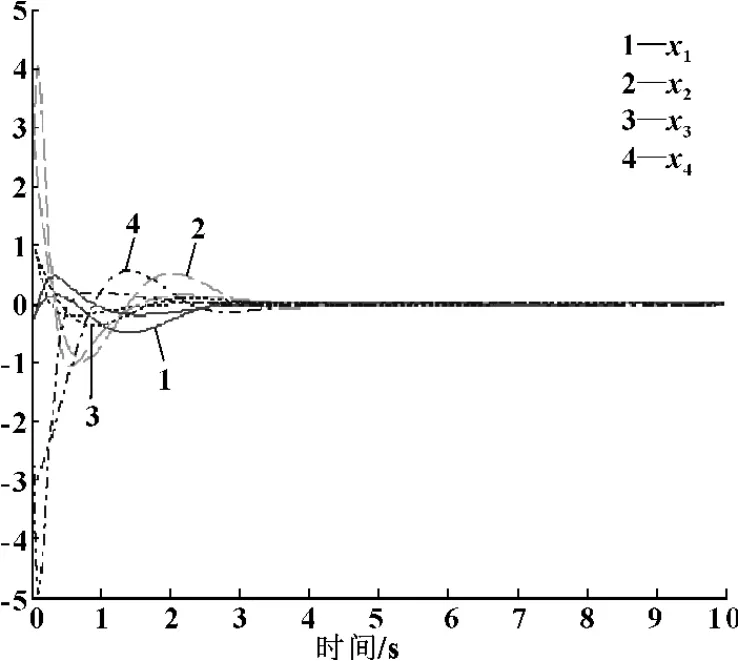
图6 离散LQR下吊车系统的状态收敛曲线(仿真1)

通过图5和图6可以看出，相比传统的极点配置方法，离散LQR方法下吊车系统各状态的收敛速度更快，从而体现了其控制优势。

为了进一步了解Q和R对于吊车控制系统的影响，下面将分别调节两个加权参数，并对比吊车系统的状态收敛曲线。首先，在原来的基础上，将Q阵修改为:

此时，吊车系统的各状态收敛曲线如图7所示。

图7 离散LQR下吊车系统的状态收敛曲线(仿真2)

根据图6和图7，可以看出，增大Q阵中的元素值后，小车速度和摆角角速度的超调量减小，说明相应的控制作用增强。

然后，在原来的基础上，修改R的值为100，这时吊车系统的各状态收敛曲线如图8所示。

图8 离散LQR下吊车系统的状态收敛曲线(仿真3)

根据图6和图8可以看出，增大R的值后，系统的调节时间延长，控制作用减小。因此，可以从实际的性能需求调节状态误差加权矩阵Q和控制量加权系数R的值。

4 结论

最优LQR理论在控制系统的设计中应用方便，求解简单，因此将其应用于吊车数字系统的控制中。仿真结果可以看出，相比传统的极点配置方法，离散LQR方法可保证吊车数控系统更优越的收敛性能。而且，离散LQR方法的调试过程较为简单，易于工程实现。但是，如果加权矩阵Q和加权系数R选择不合理，设计出来的控制系统是不满意的，此时所谓的“最优”只是使指标的最小化。通常把Q阵中的加权系数增大，则对应的状态变量会收敛的更快些，把系数R增大则对应的控制量会减小些。

［1］高丙团，陈宏钧，张晓华．龙门吊车系统的动力学建模［J］．计算机仿真，2006，23(2):50-53．

［2］李树江，胡韶华，吴海．基于LQR和变论域模糊控制的吊车防摆控制［J］．控制与决策，2006，21(3):289-292．

［3］杨斌，刘惠康，代文蕤．桥式起重机防摆控制器的设计［J］．制造业自动化，2012，34(1):122-124，131．

［4］贾诺，王辉．吊车系统的状态反馈控制的极点配置法［J］．哈尔滨师范大学:自然科学学报，2004，20(4):10-15．

［5］袁浩，徐真真，王先来．极点配置方法在起重机机架模型中的应用［J］．实验室研究与探索，2006，25(12):20-24．

［6］NAIDU D S．Optimal Control Systems［M］．FL，USA:Crc Press，2002:101-149．

［7］SHAKIR H，KIM WJ．Nanoscale Path Planning and Motion Control with Maglev Positioners［J］．IEEE/ASME Trans．Mechatronics，2006，11(5):625-633．

［8］BASINA M，RODRIGUEZ-GONZALEZA J，FRIDMANB L．Optimal and Robust Control for Linear State-delay Systems［J］．Journal of the Franklin Institute，2007，344(6):830-845．

［9］DRAGAN V，MUKAIDANI H，SHI P．The Linear Quadratic Regulator Problem for a Class of Controlled Systems Modeled by Singularly Perturbed ito Differential Equations［J］．SIAM Journal on Control and Optimization，2012，50(1):448-470．

［10］蓝会立，高远，谭光兴，等．车辆悬架LQR控制器权值优化方法［J］．科学技术与工程，2013，13(17):75-77．

［11］刘晓培．基于遗传算法的汽车主动悬架LQR控制器的优化设计［J］．组合机床与自动化加工技术，2013(6):78-80．