基于HPSO算法的磨削加工参数优化

弓清忠，吴锦松，王大镇

(1．集美大学机械与能源工程学院，福建厦门 361021;2．厦门安达兴电气集团有限公司，福建厦门 361021)

0 前言

由于特有的分子结构，工程陶瓷具有高硬度、高硬度、强耐腐蚀性、高耐热性和耐磨损的优良性能，这些优良的性能使得工程陶瓷在航空、化工、机械及电子等领域具有广泛的应用［1-2］。磨削是工程陶瓷加工的主要手段，在加工过程中，磨削参数的选择往往依靠经验手工整定调整，该方法导致了参数计算效率低和不易得到最优解的问题，而且要求加工者对材料的加工要有足够深的先验知识，因此，对工程陶瓷磨削加工过程中的参数进行优化选择，确定最优的加工参数，对实现工程陶瓷优质高效加工和磨削加工系统加工能力的充分发挥具有重要的意义［3-4］。

在智能算法的选择上，粒子群算法［5-6］是基于动物群体觅食和人类决策行为而提出的一种启发式全局优化算法，其优点是算法简单，容易编程实现，但是随着粒子群算法迭代次数的不断增加，各粒子就会越来越相似，容易陷入局部最小而无法跳出，因此引入了混合粒子群算法［7］，该方法引入了遗传算法中的交叉和变异操作，通过把粒子个体和群体极值进行交叉以及粒子自身的变异的方式来搜索最优解。

本文作者采用混合粒子群算法对工程陶瓷磨削加工过程中的参数进行优化，在2种不同的加工性能下，比较混合粒子群算法和粒子群算法的求解结果，并从中选择最优的加工参数进行磨削加工。

1 混合粒子群算法

粒子群算法是基于动物群体觅食和人类决策行为而提出的一种启发式全局优化算法。在该算法中，粒子通过个体极值Pt和群体极值Gt更新自身的速度v和位置X，其进化方程可描述为［8］:

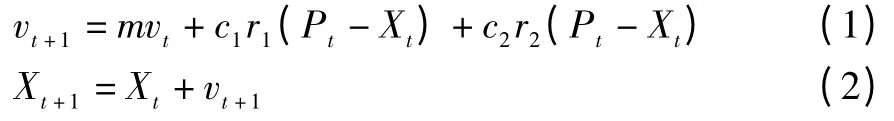
式中:m为惯性权重;c1，c2为速度更新参数;r1，r2为［0，1］区间的随机数。

为了更好平衡算法的全局搜索与局部搜索能力，w可以采用线性递减惯性权值:

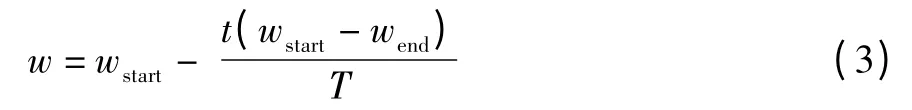
式中:wstart，wend表示初始惯性权重和迭代到最大次数时的惯性权重;t为当前迭代次数;T为最大迭代次数。

一般来说，初始惯性权重要大于迭代次数最大时的惯性权重，这样可以使粒子群算法在迭代初期由较大的惯性权重使算法保持较强的全局搜索能力，而在迭代后期由较小的惯性权重使算法进行更精确的局部搜索。但是随着粒子群算法迭代次数的不断增加，各粒子就会越来越相似，容易陷入局部最小而无法跳出，因此引入了遗传算法中的交叉和变异操作，通过把粒子个体和群体极值进行交叉以及粒子自身的变异的方式来搜索最优解。

交叉。由于粒子群个体采用实数编码，所以交叉操作采用实数交叉法，第m个染色体Am和第n个群体最优染色体An在k位的交叉操作方法为:

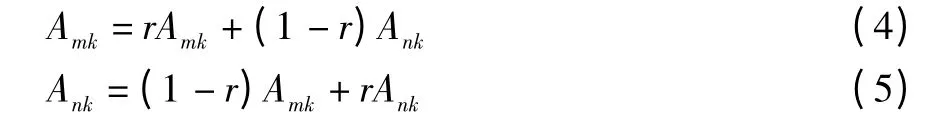
其中，r是［0，1］区间的随机数。

变异。变异操作的主要目的是维持种群的多样性。变异操作从种群中随机选取一个个体，选择个体中的一点进行变异以产生更优秀的个体，第i个个体的第个j基因进行变异的操作方法为［9］:

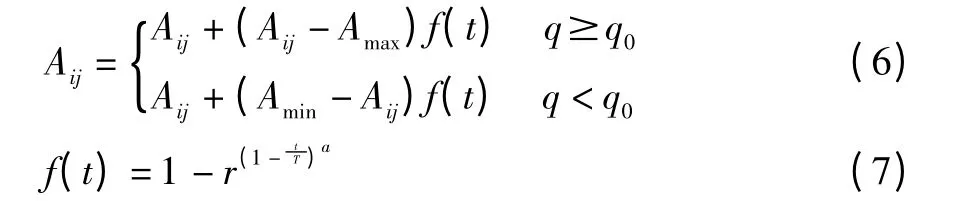
式中:Amax和Amin是个体Aij的上界和下界;r是［0，1］区间的随机数;t是当前进化代数;T是最大进化代数;a是可调参数。

2 磨削加工参数优化设计

在工程陶瓷材料的磨削加工中，材料去除率是衡量磨削加工的重要因素之一，其值越高，磨削加工的费用就越低，但是去除率的提高受到工件表面质量影响，表面质量的受损将导致材料强度的降低。根据磨削机制和影响加工效果的主要因素，工程陶瓷磨削参数的优化模型为［10］:

为了便于智能算法的优化求解，将式(8)取负数，转化为求极小值的问题，其表达式为:

式中:F(X)为材料去除率;f为工件线速度;dc为切削深度。

优化模型式(9)满足如下约束条件:

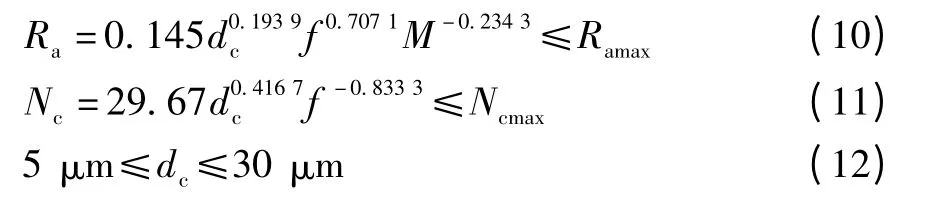
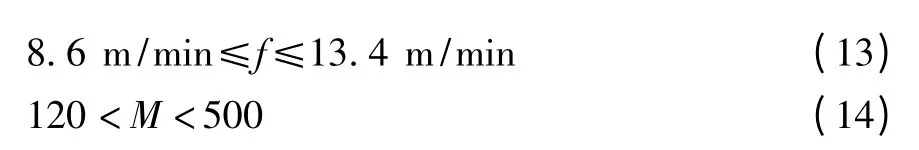
上述约束条件中，Ra为工件的表面粗糙度，Ramax为工件的最大表面粗糙度，Nc为刮伤数，Ncmax为最大刮伤数，M为砂轮速度。

选择优化参数向量为X=［dcf M］，适应度函数为式(9)，设置混合粒子群算法的群体数为100，惯性权重wstart，wend分别为0．9和0．4，速度更新参数c1，c2都为2，变异概率为0．6，交叉概率为0．01，则混合粒子群算法的流程图如图1所示。

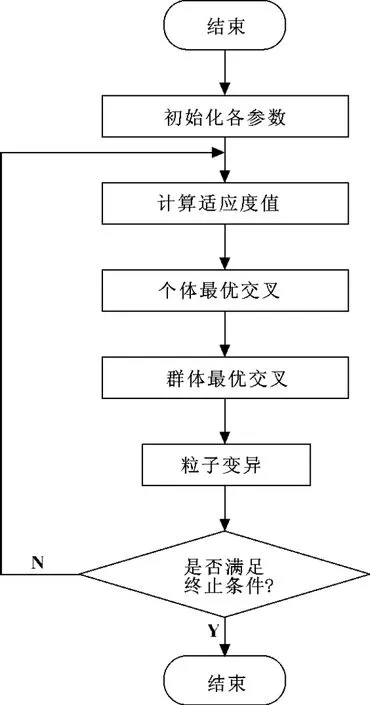
图1 混合粒子群算法流程图

3 参数优化设计结果与分析

选取2种加工性能要求下的情况来加工工程陶瓷材料，其中性能一要求为:Ncmax=7，Ramax=0．3;性能二要求为:Ncmax=9，Ramax=0．4;分别采用遗传算法(GA)，粒子群算法(PSO)，二次规划算法(NLPQL)和文中的混合粒子群算法(HPSO)对两种性能情况下的磨削参数进行优化求解，其求解结果如表1所示。

由表1的计算结果可知，采用4种方法对磨削参数进行优化都能达到目标，而采用混合粒子群算法的求解结果在两种加工性能要求下材料去除率均为最大，其求解结果要优于其他算法的求解结果，说明混合粒子算法在搜索最优解的能力更强。

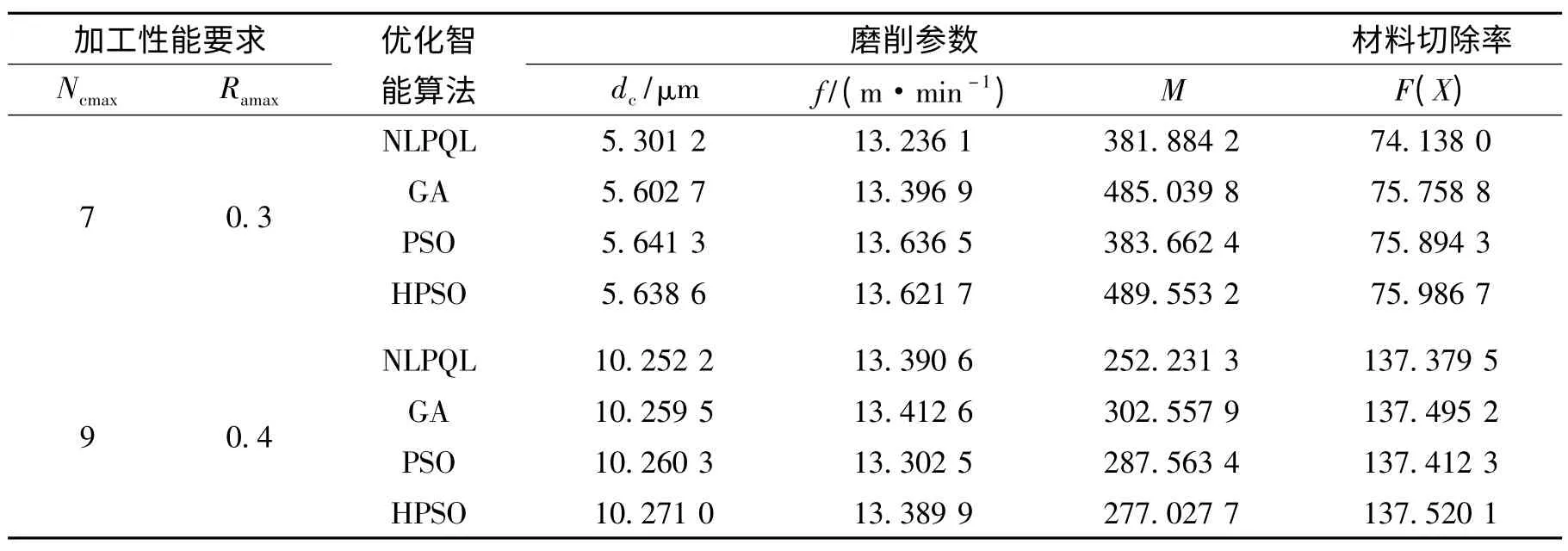
表1 磨削参数优化结果

4 结论

针对工程陶瓷磨削过程中的参数选择优化问题，采用混合粒子群算法进行求解，并给出了该方法的设计步骤和方法，同时针对2种不同的加工性能要求，比较了4种智能优化算法的结果。结果表明采用混合粒子群算法得到的结果要优于其他方法，说明它能更好地用于陶瓷磨削过程中的参数优化选择，也可以将其用于其他材料的磨削加工参数优化选择中。

［1］谢桂芝，尚振涛，盛晓敏．工程陶瓷高速深磨磨削力模型的研究［J］．机械工程学报，2011，47(11):169-175．

［2］王锋，吴永海．基于iSIGHT的工程陶瓷磨削加工参数优化研究［J］．矿山机械，2009，37(22):1-4．

［3］李伯民，赵波．现代磨削技术［M］．北京:机械工业出版社，2004．

［4］王海涛，刘伟强，杨建国．基于RBF神经网络的磨削表面粗糙度预测模型［J］．机床与液压，2014，42(3):107-111．

［5］解红霞，石连文，常燕臣．混合粒子群算法在液压钻机控制中的应用［J］．液压与气动，2011(12):69-71．

［6］管欣，逄淑一，詹军．汽车悬架运动学特性参数优化方法［J］．哈尔滨工业大学学报，2011，43(1):145-148．

［7］付涛，王大镇，弓清忠．基于混合粒子群算法的柴油机喷油器可靠性分布的参数估计［J］．机械强度，2014(4):145-148．

［8］史峰，王辉．MATLAB智能算法30个案例分析［M］．北京:北京航空航天大学出版社，2011．

［9］孙光永，李光耀，钟志华．基于序列响应面法的汽车结构耐撞性多目标粒子群优化设计［J］．机械工程学报，2009，45(2):224-230．

［10］LEE T S，TING T O，LIN Y J，et al．An Investigation of Grinding Process Optimization Via Evolutionary Algorithms［C］//Proceedings of the 2007 IEEE Swarm Intelligence Symposium．Honolulu，United States，2007:176-181．