结合大涡模拟的格子玻尔兹曼方法模拟高雷诺数流动

刘祖斌，赵鹏

（1浙江大学海洋工程系，杭州310058；2英伟达半导体科技（上海）有限公司，上海201210）

结合大涡模拟的格子玻尔兹曼方法模拟高雷诺数流动

刘祖斌1，赵鹏2

（1浙江大学海洋工程系，杭州310058；2英伟达半导体科技（上海）有限公司，上海201210）

为了将格子玻尔兹曼方法（Lattice Boltzmann method）推广到高雷诺数流动的数值模拟上，文章研究了将大涡模拟的Smagorinsky模型及其改进的IR模型应用到LBM方法中并发展了LBM-SM模型和LBM-IR模型，其后以顶盖驱动方腔流动（Re=1 000；10 000；100 000）和后台阶流动（Re=389；1 000；10 000；100 000）为标准进行数值模拟与比较。数值结果说明该方法可以应用于高雷诺数流动的数值模拟，并克服了传统LBM方法在模拟高雷诺数流场时会出现非物理振荡的情况。通过分析对比，不仅得到了两种模型能够稳定计算且不失真的参数范围，并且认为LBM-IR模型有效参数的选取范围更为广泛。

Lattice Boltzmann method；大涡模拟；高雷诺数；LBM-SM；LBM-IR

0 引言

格子玻尔兹曼方法（LBM，Lattice Boltzmann Method）是一种新兴的计算流体力学数值模拟方法。它从分子运动论和统计力学的观点和理论出发，建立微观粒子的运动模型，用流动和碰撞两个简单的过程模拟流动的宏观特性[1-3]。该方法具有计算过程简单，复杂边界问题处理十分灵活方便，计算局部性强，具有天然的并行性，非常适合在大规模并行计算机上运行[4]。因此，自从上世纪末期该方法发展以来，对其的研究与应用也成为了当今计算流体力学热点。然而问题同样也存在，LBM方法是一种直接数值模拟方法（DNS，Direct Numerical Simulation），在足够细的计算网格下可以模拟高雷诺数的流动问题，但是受到计算条件以及计算成本的限制，计算往往很难做到非常大的网格规模，同时由于在导出Navier-Stocks方程的过程中有低马赫数（Ma＜0.3）的要求。综合以上两点，在使用LBM方法进行数值模拟时，流场雷诺数会受到一定限制。

大涡模拟是当今流体力学研究的热门课题之一，作为研究湍流的主要手段之一在未来将有更为广泛的应用[5]。大涡模拟的基本思想是采用各种滤波方法将那些控制动量输运等的大尺度涡与小尺度涡分离。大尺度涡应用数值模拟方法直接求解，可以获得大尺度流动的动态特征，而小尺度涡则采用亚网格模式模拟。使用大涡模型所需要的网格数目很大，若要求能分辨出最小尺度也就是Kolmogorov尺度的涡，则网格数目将正比于Re9/4，因此在高雷诺数流动情况下的计算效率非常低下。

将大涡模拟的模型应用于LBM方法中是解决此问题的一个有效方法。这个思想，可追溯到LBM方法建立初期，陈十一等[6]曾进行过高雷诺数方腔流动的模拟，后来国内外有不少从事大涡模拟研究的学者[7-11]也结合起来研究，但所应用的模型太少，没有引起足够的重视。本文将大涡模拟的Smagorinsky模型及其改进的IR模型应用到LBM方法中，分别对二维的顶盖驱动方腔流动和后台阶流动进行了数值模拟。方腔流动的雷诺数的取值范围从1 000到100 000，并且与已有的数值标准解进行了对比，其结果符合得较好；作为该方法的扩展，本文给出了高雷诺数的后台阶流动，雷诺数分别取了10 000，100 000，并给出了相应的分析。

结合大涡模拟的LBM方法（LBM-LES）可以在很大程度上提高数值模拟中的雷诺数，又具有直接数值模拟的精细分辨率和LBM的良好并行性能，将会推动直接数值模拟（DNS）的更广泛应用。

1 LBM方法

LBM方法是一种模拟流体流动的数值方法，它不再基于连续介质假设，而是把流体看成由许多只有质量没有体积的微粒组成，这些微粒可以向空间的若干方向任意流动。它的主要思想就是以简单规则的微观粒子运动代替复杂多变的宏观现象。粒子在每个时间步的运动由流动和碰撞两步构成：碰撞，当多个粒子到达同一网格结点时，它们按碰撞规则相互作用并重新分布；流动，每个粒子按其速度方向移动到最近的网格结点。

1992年，Qian（钱跃竑）等人[2-3]提出LBM方法的单松弛模型，即：LBGK（Lattice Bhatnagar-Gross-Krook）模型。目前，LBGK模型是格子玻尔兹曼方法中应用最广泛的模型。LBGK模型来源于LGA（Lattice Gas Automator），继承了空间离散速度离散的原则和流动碰撞的简单运动，抛弃了Fermi-Dirac分布及粒子碰撞理论，采用Maxwell平衡态分布和BGK碰撞理论（由Bhatnager，Gross，Krook提出），使得各向同性、Galilean不变性和压力独立于流速等条件都得到满足。再用单松弛时间逼近碰撞项，其对应的玻尔兹曼演化方程为：

其中：ω为松弛因子，ω在0到2之间，小于1为亚松弛，大于1为超松弛。fi为单粒子分布函数，表示在t时间上，x格点上速度为ei的有1个粒子的概率；ei称为粒子运动速度或离散速度；为平衡态分布函数，是流体动力学量（如密度，动量等）的函数。方程左侧为流动项，右侧即为碰撞项。由此方程可以看出，碰撞过程只与本节点有关，为局部计算过程，流动步也仅与相邻的网格点之间进行数据交换。因此，该方法具有天然的并行性能。LBGK模型中的DnQb系列模型的分布函数为：

其中：cs为声速，ti为对应粒子速度的权系数，u为宏观速度，ρ为宏观密度。为了保证得到正确的宏观Navier-Stocks方程，需要通过使满足质量守恒、动量守恒等约束条件来得到正确的权系数。

DnQb系列模型的粘性系数为：

对于本文所选用的D2Q9模型，权系数和离散速度的选取如下：

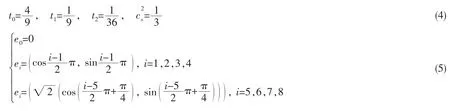
2 结合大涡模拟的LBM方法

2.1 大涡模拟及其模型

大涡模拟的基本思想是直接数值模拟大尺度结构，而小尺度结构（其尺度小于计算网格尺度）对流场的大尺度结构不敏感依赖，通过建立亚网格模型（Subgrid Scale，SGS）来模拟。

其中：τij为湍流亚网格应力

其次，大涡模拟最重要的就是给出正确的亚网格模型。最早提出且应用至今的是Smagorinsky模型，这是由气象学家Smagorinsky于1963年提出的。该模型认为亚格子湍流具有混合长度型的涡粘系数，混合长度与过滤尺度同一量级，属于唯象涡粘模型。其优点是简单，并可以通过调整参数获得相当好的结果；缺点是完全属于耗散型的，没有考虑从小尺度到大尺度的能量逆转。后人在此基础发展了诸多模型，如Smagorinsky-Lilly模式，及动力学模式等[7]。

Smagorinsky模型中亚网格应力中的非各向同性部分正比于湍流涡粘性系数与大尺度变形率张量的乘积，

其中：δij是Kronedcker δ函数，vt是涡粘系数，C是Smagorinsky常数，是大尺度应变率张量的模：

由于Smagorinsky常数的取值对计算的结果影响较大，而通常的模型如Smagorinsky-Lilly模式对取值缺乏判定的依据，所以针对该常数的机理性探讨非常有价值。2005年Mayers和Saguat[11]提出一个改进的Inetial-Range模型，认为模型系数C强烈依赖于两个比值，即：大涡模拟的滤波尺度与Kolmogorov尺度的比值Δ/η和宏观尺度与滤波尺度的比值L/Δ，具体的关系参照文献。在实际应用中，他们给出了在无穷大雷诺数条件下的极限值C∞=0.18，在以下计算中，我们将对此进行验证。

2.2 格子Boltzmann大涡模拟方法（LBM-LES）

在LBM方法中引入大涡模拟模型的方法，首先给出LBM方法中的滤波形式，对粒子的分布函数fi（平衡态函数）定义滤波后的形式为：

然后对Boltzmann方程的微分形式进行滤波，得到滤波Boltzmann方程

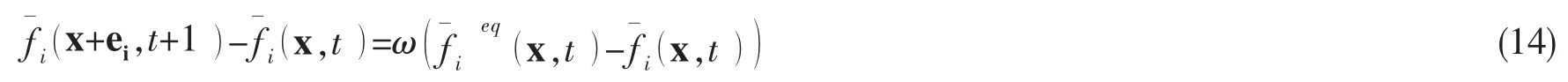
在LBGK模型中，所有格子的间距均为1，这样就使得物理空间的滤波对格点上的分布函数保持不变，且松弛时间与平均自由程等价，所以松弛时间的改变就等价于改变局部平均自由程，从而改变了局部粘性。总的粘性系数vt与松弛时间τt的关系仍然保持通常方法中的形式：

物理运动粘性在流动过程中保持不变，而流动结构的变化会改变涡粘性系数。总的粘性系数由物理运动粘性系数v0和涡粘性系数vv组成：

Smagorinsky模型[7-10]，

Inetial-Range模型[11-14]，

其中：C和C*为模型常数，其取值范围在0－2之间，Δ取网格长度为1。

从以上计算公式中可知，局部涡粘性系数是由局部应变率张量来求得，而相比于其他差分法的复杂，在格子玻尔兹曼方法中可通过局部非平衡态分布函数简单求得，这也是相比于单纯大涡模拟的一个优势。结果如下：

滤波非平衡动量流张量，

滤波局部应变率张量，

因此得到加入两个模型的格子波尔兹曼方法的最终松弛时间的表达式：

LBM-Smagorinsky模型（LBM-SM），

LBM-Inetial Range模型（LBM-IR），

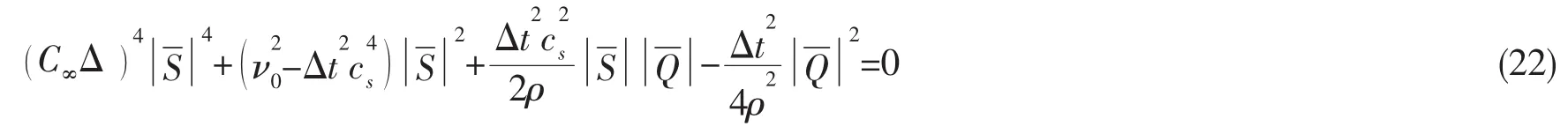
3 数值算例

3.1 标准顶盖方腔驱动流

标准顶盖方腔驱动流是经典的粘性不可压缩流动数值模拟的算例，从上个世纪六十年代初被提出后已经研究了四十余年，该模型问题通过假定流体四周均为固体壁面而避免了物理上复杂的进口和出口。由于它整个流场形状规则，边界条件简单，因此便于计算、分析和比较[15]，成为检验计算流体力学方法的最广泛算例。

该问题的数学模型是假设一个宽度为1的正方形腔内充满流体，左右和底面均固定，在顶部有一平板以固定速度由左向右移动。本文使用的计算分辨率为256×256，平板移动速度为0.1。在本文以下的结果中，将速度与网格均做归一化处理，以便于与标准解[16]对比。

驱动方腔流动过程中存在转捩过程，在高雷诺数下由层流转变为湍流的过程中存在一个雷诺数区间［Re1，Re 2］，5 000＜Re1＜=7 500，Re2＞10 000。当Re在［Re1，Re 2］时，驱动方腔的流动存在非定常周期解；当Re＜Re1时存在稳定的层流解，而当Re＞Re2时驱动方腔的流动完全转变为湍流。

下面将给出雷诺数为1 000，10 000，100 000的结果。作为对基本算法的检验，对于雷诺数为1 000和10 000的数值模拟，我们比较了DNS和两种不同的组合模型的结果，并与基准解（Benchmark）进行了比照，验证了模型的准确性。而对于大雷诺数，由于DNS已无法模拟，直接给出数值模拟的结果。本文在计算中专门对模型系数C进行了敏感性测试，以0.02为步长对0-2的区域均进行了模拟计算。

Re=1 000时，流动较稳定，属于层流阶段。本文采用了三种方法进行了数值模拟，如图1，其中方格、三角、虚线、实线分别代表数值基准解、LBM方法直接数值模拟、LBM-SM模型和LBM-IR模型结果，并且给出了两条中心线上的速度分布值。由图1可以看出标准的LBM方法与LBM-SM模型和LBM-IR模型所得的结果都对标准解吻合得很好。在模型系数选取方面，LBM-SM模型在全部取值都能完成计算，其中C=0.1能得到最好的结果；LBM-IR模型测试结果是同样的情况。

当Re=10 000时，图2给出了其几何中心线上的速度图，并与标准解进行对比，符合依然很好。但在细节上速度产生了周期性现象，图4给出了方腔左下方点（0.78，0.78）速度周期变化的图示。LBMSM模型在模型系数小于0.1区域能得到正确的流场，在0.04附近能得到最好的效果，而大于0.1会逐渐抹平边角区的小涡结构。LBM-IR模型在大于0.1依然能得到较好的效果，在C=0.18附近效果最好。计算结果说明，模型系数C的合理取值范围较小是标准Smagorinsky模型的一个缺点，而且系数的选取没有合理的依据，而IR模型在取值的合理性和有效性方面有较大提高。

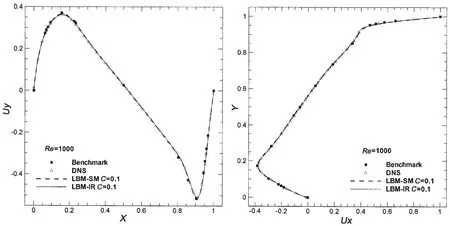
图1 Re＝1 000时，几何中心垂直线上的速度u分布和速度v分布Fig.1 Re=1 000,u-velocity and v-velocity distribution in geometry center vertical line

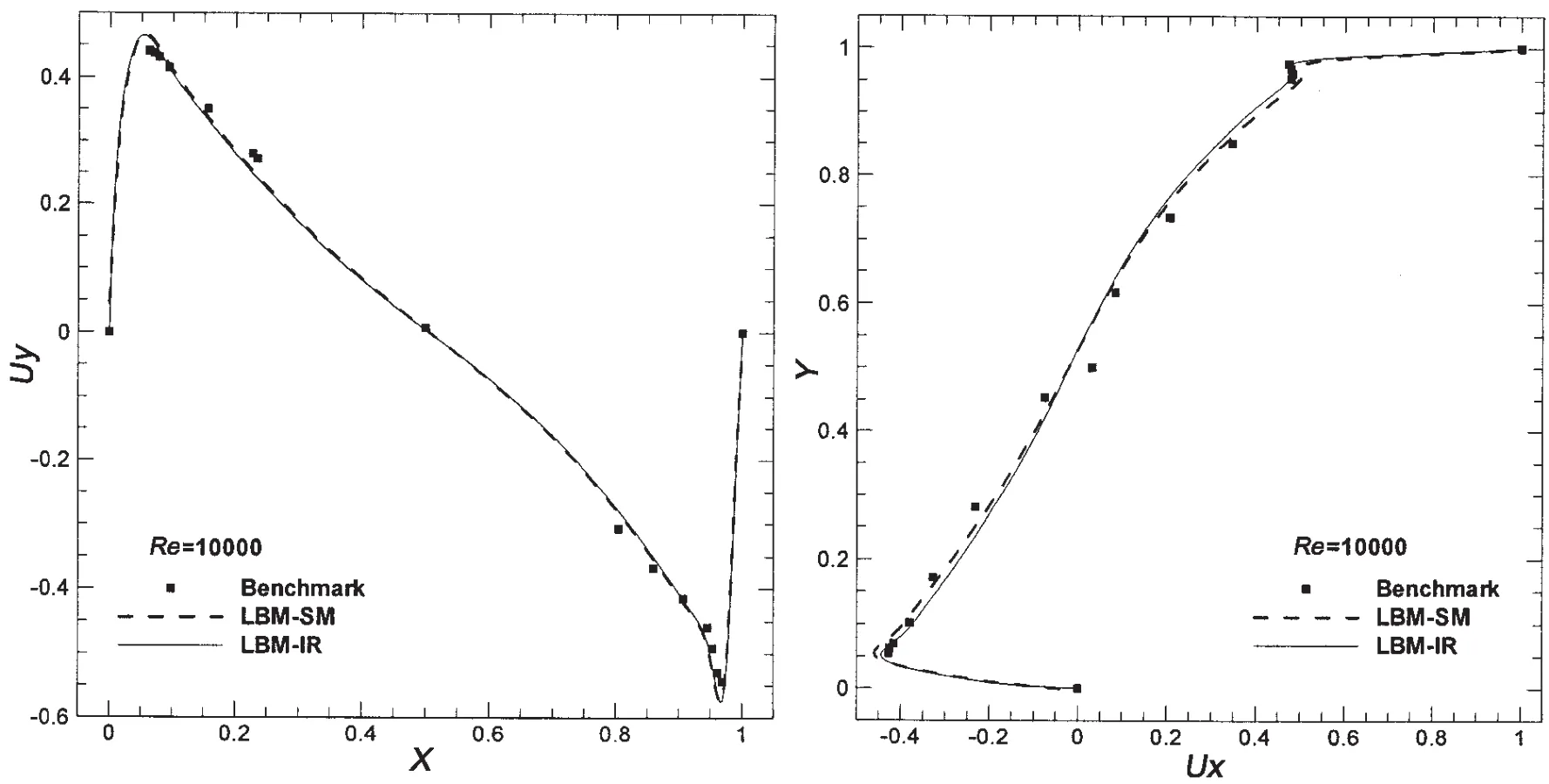
图2 Re＝10 000时，几何中心垂直线上的速度Ux分布和速度Uy分布Fig.2 Re＝10 000,Ux-velocity and Uy-velocity distribution in geometry center vertical line

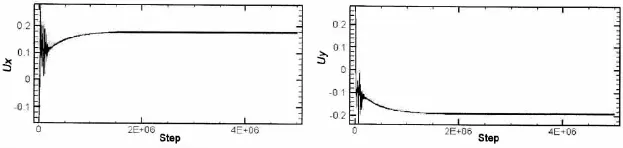
图3 Re＝10 000时，左下方点（0.78，0.78）X和Y方向速度随时间的演化图Fig.3 Re＝10 000,evolution of Uxand Uywith time at bottom left dot(0.78,0.78)

Re=100 000时，流动已完全进入了湍流阶段。由于此时LBM方法会由于松弛因子太接近于2而出现很强的非物理数值现象，LBM-SM模型能保证不出现数值发散的区域也相对较小，在C=0.1附近；LBM-IR模型相对区域较大，在C=0.28附近。

3.2 后台阶流动

分离再附现象是实际工程中经常遇到的流动问题，如机翼分离涡的再附、冲压发动机燃烧室内的流动、流体经过截面突扩的管道后的流动等等。为改善流动状态、加强燃烧、强化换热以及有利于混合物的掺混等，对这一流动进行研究是十分必要和有意义的。后台阶流动由于其分离点稳定、边界条件简单，实验方便，成为研究分离再附运动中最简单也是最典型的流动。

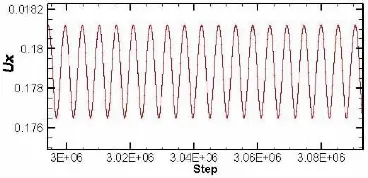
图4 Re＝10 000时，左下方点（0.78，0.78）X方向速度随时间的演化图（局部放大图）Fig.4 Re＝10 000,enlarged partial view of evolution of Ux-velocity with time at bottom left dot(0.78,0.78)

在后台阶流动中，台阶后缘会产生类似平板剪切层的大涡序列，上下壁面处会出现一系列附着涡。从而，台阶后缘的剪切层，扩张段的分离区以及下游充分发展的槽道流，成为后台阶流动的三个主要流动组成。从20世纪70年代开始，许多研究者都对后台阶流动进行了实验研究和数值模拟[17-19]。

后台阶流动的粘性不可压流体的控制方程为：

这里u=（u，v，）w为速度场，p为压力，雷诺数Re定义为：

其中：Um为入口最大速度，D为特征尺度，此处为台阶高度，即D=h，h为台阶高度，ν为流体的运动粘性系数。

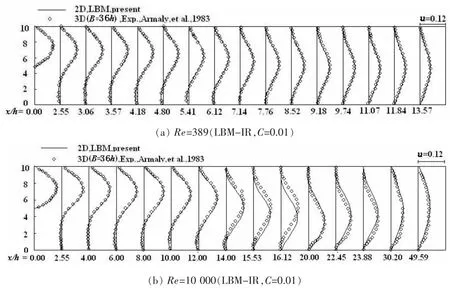
图5 后台阶流动的不同位置的速度剖面图，（a）Re＝389，（b）Re＝1 000Fig5 Velocity profiles of backward facing step flow in variety of places,(a)Re＝389,(b)Re＝1 000

本文应用LBM-IR模型对二维高雷诺数的流动做了数值模拟。使用传统的DNS进行数值模拟时，模拟高雷诺数流动需要加密计算网格，使得计算时间、计算成本都很高，但将LES与LBM结合的模型能够较好地解决这一问题。本文在4 000×100的网格上模拟了Re为389，1 000，10 000，100 000的流动。如图5所示，在雷诺数为389和1000的结果中，我们比较了不同位置速度剖面与实验值[15]的比照，验证了该模型的准确性。

如图6所示，当雷诺数达到10 000，100 000的时候，在台阶后方形成了一系列旋涡，与理论的预测一致。图（a），（b）分别给出了两个雷诺数时台阶之后的流动瞬时涡量云图。此时的流动已经发展为湍流，传统的LBM方法不能直接进行数值模拟。而通过本文提出的LBM-LES方法能够在不增加分辨率的情况下捕捉到流动的细节信息。由图可以看出，在台阶之后先出现了一些小涡，随着时间的推进，小涡逐渐合并形成了大结构的涡。并且我们的算法也能够获取大涡中更为复杂的结构。

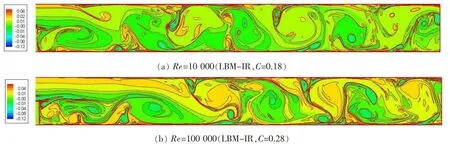
图6 后台阶流动的涡量分布图，（a）Re＝10 000，（b）Re＝100 000Fig.6 Voticity contours of backward facing step flow,(a)Re＝10 000,(b)Re＝100 000

4 结论

本文将LES湍流模型加入到LBM方法中组合成为LBM-LES模型不仅在理论上是完全可行的，以上算例也很好地验证了这类模型的准确性。通过对高雷诺数的标准顶盖驱动方腔流动和后台阶流动的模拟，并与标准解进行对比以及理论分析可以得到以下结论：

（1）使用LBM-SM模型和LBM-IR模型进行模拟过程中，分别得到了不同雷诺数的最佳模型系数取值范围，而这个结果并不完全是一个确定的值，是与雷诺数相关的。

（2）在两个组合模型的对比中可以发现LBM-IR模型不仅具有更完整的系数确定依据，而且在系数取值范围上有较大的提高。

本文研究的两个模型具有普遍意义，对于大涡模拟的涡粘模型可以依据本文理论推导加入到LBM方法中，因此LSM-LES模型可以得到可持续的发展。而对于该类模型的详细研究还是很有必要，尤其在模型系数敏感性上，寻求最佳的系数将对模拟结果的精确度产生关键的作用，本文作者将深入研究。

[1]郭照立,郑楚光,李青.流体动力学的格子Boltzmann方法[M].武汉:湖北科学技术出版社,2002.

[2]Qian Y H,d’Humieres D,Lallemand P.Lattice BGK models for the Navier-Stokes equation[J].Euro phys Lett.,1992(17): 479-484.

[3]Qian Y,Succi S,Orszag S.Recent advances in lattice Boltzmann computing[J].Ann.Rev.Comp.Phys.,1995,3:195-242.

[4]赵鹏,张丹丹,汪鲁兵等.格子Boltzmann并行程序的优化与性能分析[J].微电子学与计算机,2008,25(10):185-188.

[5]崔桂香,许春晓,张兆顺.湍流大涡数值模拟进展[J].空气动力学报,2004,6,22(2):121-129. Cui Guixiang,Xu Chunxiao,Zhang Zhaoshun.Progress in large eddy simulation of turbulent flows[J].ACTA Aerodynamica Sinica,2004,6,22(2):121-129.

[6]Hou S,Sterling J,Chen S,Doolen G D.A lattice Boltzmann subgrid model for high Reynolds number flows[M].In: Lawniczak AT,Kapra lR,editors.Pattern formation and lattice gas automata.Fields Institute Communications 6,Providence,RI:AMS,1996:66-151.

[7]Guan H,Wu C J.Large-eddy simulations of turbulent cavity flows with the dynamic SGS model and LBM algorithm[J]. Transactions of Nanjing Univ.of Aeronautics&Astronautics,2001,18(Suppl.):60-63.

[8]杨帆,刘树红,唐学林,吴玉林.格子Boltzmann亚格子模型的研究[J].工程热物理学报,2004,S1. Yang Fan,Liu Shuhong,Tang Xuelin,Wu Yulin.Study of subgrid turbulence model for lattice Boltzmann method[J]. Journal of Engineering Thermophysics,2004,S1.

[9]Yu H,Girimaji S S,Luo L S.DNS and LES of decaying isotropic turbulence with and without frame rotation using Lattice Boltzmann methods[J].J Comput.Phys.,2005,209:599-616.

[10]Burattini P,Lavoie P,Agrawal A,Djenidi L,Antonia R A.Power law of decaying homogeneous isotropic turbulence at low Reynolds number[J].Physical Review E,2006,73,066301.

[11]Meyers J,Sagaut P.On the model coefficients for the standard and the variational multi-scale Smagorinsky model[J].J Fluid Mech,2006,569:287-319.

[12]Meryers J,Sagaut P.Evaluation of Smagorinsky variants in large-eddy simulations of wall-resolved plane channel flows [J].Physics of Fluids,2007,19(9):1-12.

[13]Dong Y H,Sagaut P,Simon M.Inertial consistent subgrid model for large-eddy simulation based on lattice Boltzmann method[J]Physics of Fluids,2008,20(3):1-12.

[14]董宇红,周亦航,邓义求.基于格子Boltzmann方程的大涡模拟对湍流时空关联性的研究[J].北京理工大学学报, 2012,32(8):876-880. Dong Yuhong,Zhou Yihang,Deng Yiqiu.Time-space corrections of isotropic turbulence by lattice Boltzmann based large eddy simulation[J].Transactions of Beijing Institute of Technology,2012,32(8):876-880.

[15]Ghia U,Ghia K N,Shin C T.High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]J Comput.Phys.,1982,48:387-411.

[16]Armaly B F,Durst F,Rereira J C F,Schonung B.Experimental and theoretical investigation of backward facing step[J].J Fluid Mech.,1983,127:473-496.

[17]Kim J,Moin P.Application of a fractional-step method to incompressible Navier-Stokes equations[J].J Comput.Phys., 1985,59:308-323.

[18]王小华,樊洪明,何钟怡.后台阶流动的数值模拟[J].计算力学学报,2003,20(3):361-365. Wang Xiaohua,Fan Hongming,He Zhongyi.Numerical simulation of backward facing step flow[J].Chinese Journal of Computational Mechanics,2003,20(3):361-365

[19]王广超,廖国勇.后台阶流动的非均匀格子Boltzmann方法模拟[J].计算机与现代化,2007,1:6-9. Wang Guangchao,Liao Guoyong.Non-uniform lattice Boltzmann method simulation of backward-facing step flow[J].Computer&Modernization,2007,1:6-9.

High-Re flow simulation with Lattice Boltzmann method combined with LES

LIU Zu-bin1,ZHAO Peng2
(1 Departement of Ocean Engineering,Zhejiang University,Hangzhou 310058,China; 2 NVIDIA Semiconductor Technology(Shanghai)Co.,Ltd,Shanghai 201210,China)

A kind of lattice Boltzmann method(LBM)combined with LES models was proposed.Smagorinsky(SM)model and improved model Inetial Range(IR)model were used to extend LBM computation scales for high Reynolds number.Simulations are performed for typical cases of high Reynolds number,cavity flow (Re=1 000;10 000;100 000)and back facing step flow(Re=389;1 000;10 000;100 000),and results are compared with benchmark results.The comparison shows that both the LBM-SM and the LBM-IR models behaved well to match the accurate solutions and could conquer the problem of oscillation caused by LBM. The analysis and comparison of the two models illustrate that the LBM-IR model has an advantage of wider area of valid model coefficient.

Lattice Boltzmann method;Large Eddy Simulation;High Reynolds number;LBM-SM;LBM-IR

O35

A

10.3969/j.issn.1007-7294.2015.05.002

1007-7294（2015）05-0484-09

2014-12-05

国家自然科学基金（10625210）；上海市教委项目基金（08ZZ43）

刘祖斌（1983-），男，博士后，E-mail：liuzb@zju.edu.cn；

赵鹏（1980-），男，高级GPU架构工程，E-mail：patricz@nvidia.com。