超精密机床主轴回转误差在线测试与评价技术* ＊

孙郅佶 安晨辉 杨 旭 张清华 王 健 毕 果

(①成都精密光学工程研究中心，四川 成都610041;②厦门大学机电工程系，福建 厦门361005)

随着机床精度的不断提高，超精密加工机床从精密机械领域不断向光学加工领域迈进，尤其是超精密切削机床，以其高精度、高确定性和高效率等优势，被广泛应用于各种高精度模具及光学元器件的加工［1-2］。成都精密光学工程研究中心采用超精密飞刀切削机床装载大圆弧刃刀具切削光学元件，表面粗糙度可以达到2 nm 以内。近年来国内在超精密机床的设计制造方面投入了巨大的精力，在切削、磨削、子口径抛光和磁流变抛光等超精密加工设备研制方面取得了重要突破，很大程度上突破了欧美对我国相关设备的垄断与技术封锁［3-6］;但是，在超精密加工机床的研制以及工艺研究中至关重要的超精密检测技术发展较为滞后，严重制约了机床研制与工艺水平的进一步提升。

主轴是超精密机床的重要部件，主轴的回转误差将直接影响机床的整体性能。以往国内超精密机床主轴回转精度的评价，只能采用准静态离线测量方式，这与主轴高速旋转的实际工况有很大差异，且测量精度也达不到亚微米级［7-11］。而目前超精密机床多采用精密气浮轴承，其回转精度可达几十纳米，必须开发一套高精度在线测试系统，能够实现主轴不同方向误差信号的高速在线采集，并进行离线分析处理以获得具有实际工程意义的参数化评价指标，并对主轴的误差来源、作用机制与影响程度进行分析。

本文基于美国Lion Precision 公司的SEA(spindle error analyzer)系统进行主轴回转误差的多通道数据采集。该系统硬件部分主要由一个双头标准球杆和5 个通道的电容位移传感器组成。该套系统的数据传输和内部算法是完全封闭的，自带软件只能得到不连续的有限参数评价，无法满足连续测量与数据深度分析的要求。因此需要采用高速数据采集卡直接读取各通道的模拟数据，并进行滤除干扰、多通道数据转换以及参数化合成处理。该系统可进行连续数据采集，具备完善的频率分析功能，以及客观的参数化指标评价功能，以实现纳米量级超精密机床主轴误差的在线测试与离线分析评价目的。

1 主轴回转误差在线测试模块组成

1.1 在线测试硬件模块构成

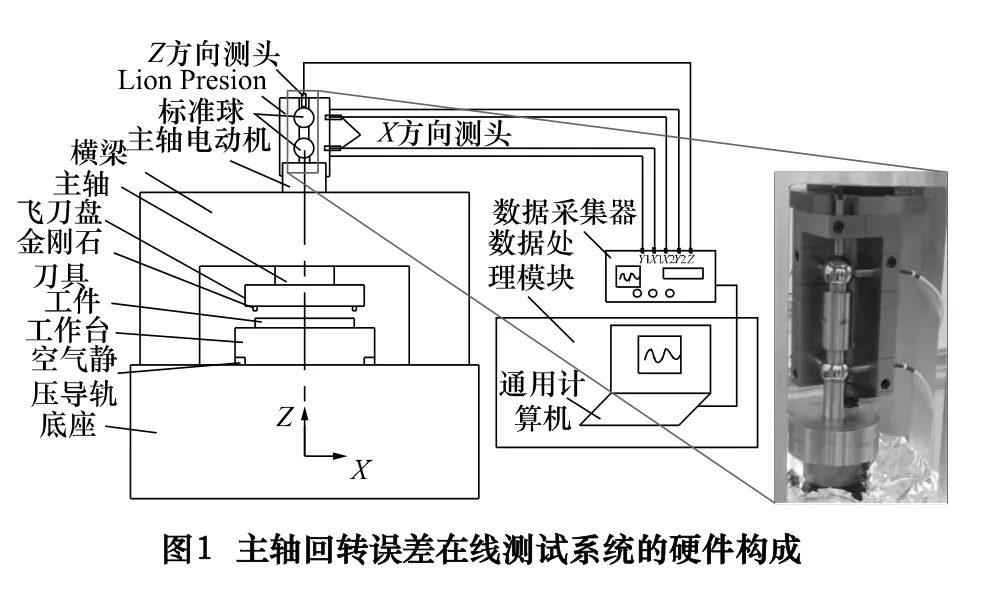
图1 为主轴回转误差在线测试系统的硬件构成。它主要由超精密切削机床、标准球杆、电容位移传感器、夹持调整系统、模拟量采集模块以及通用计算机等部分构成。测试对象为一台立式超精密飞切加工机床，大圆弧刃天然金刚石刀具固定在大飞刀盘的外缘做高速旋转，工件则固定在工作台上做水平方向进给，从而完成平面光学元件加工任务。该超精密机床主轴采用气浮轴承支撑，由直连在主轴上的电动机轴提供驱动，若在一定转速范围内认为主轴旋转部分为刚体，则通过测量主轴尾端部的5 个方向的位移规律，可以换算出固定于主轴头端部刀尖部位的运动特征。因此在主轴尾端部固定双头

标准球杆如图1 所示，并采用Lion Precision 的电容位移传感器进行5 通道的精密测量，分别是下部标准球的X、Y方向，以及上部标准球的X、Y、Z方向，标准球杆的圆度误差优于30 nm，电容位移传感器的分辨率为2 nm。对采集到的5 通道位移信号采用Zonicbook618E 高速数据采集模块进行采集和存储记录，并编制软件对采集的数据进行分析处理。整个采集过程在实际工艺加工过程中在线实施。

1.2 回转误差数据处理基本流程

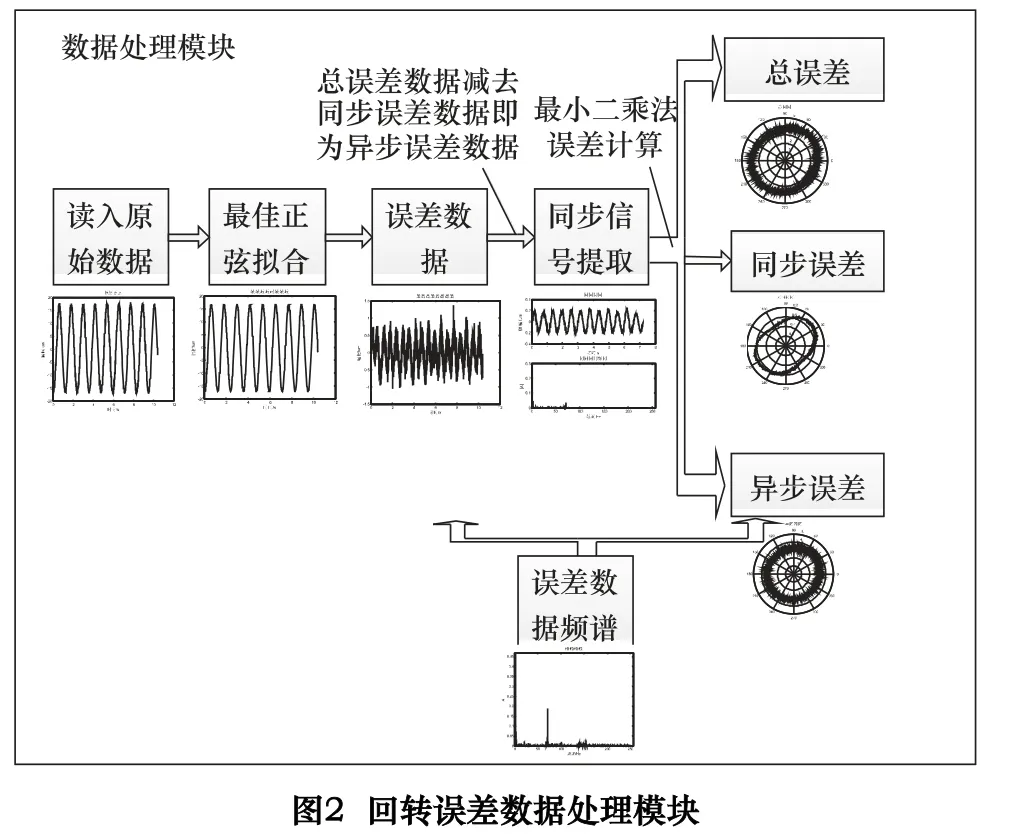
由数据采集模块获得的5 通道位移数据含有干扰信号及标准球杆安装偏心等误差数据，且需要将数据转换成具有评价意义的轴向误差与径向误差的方式，因此需要对数据进行处理。图2 所示为数据处理的基本流程，首先将上端X、Y通道和下端X、Y通道的数据分别合成为该处轴心在水平面内的运动轨迹，并通过正弦拟合方式去除安装偏心;然后采用梳状滤波器提取同步误差信号;最后由总误差减去同步误差信号，再进行工频干扰抑制等处理获得异步误差信号，获得主轴旋转误差的各项精度指标。

2 回转误差评价算法

如图3 所示为自主开发的主轴回转误差计算流程图，整个流程通过合理去除测量误差，提取有效的误差信号，按照实际需求对误差进行不同方向分离，并进行图像化展示和误差频谱分析。

2.1 去除安装偏心

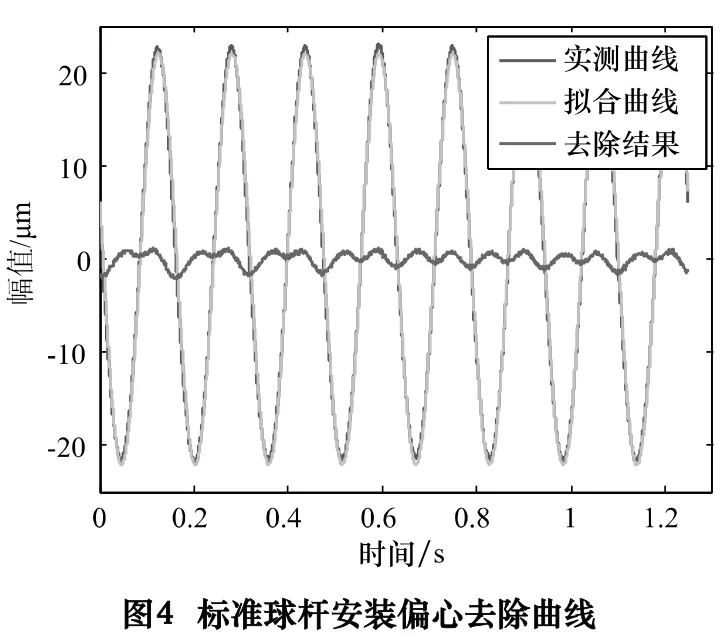
首先读入由Lion Precision 测得的主轴回转误差模拟量信号。由于安装Lion Precision 的标准球杆时，标准球中心与主轴旋转轴线之间不可避免存在一个固定偏心量，测量时该偏心会引入一个标准正弦误差，以往学者均采用傅里叶变换去除一阶信号的方式去除该偏心［11］。由于本文的测量对象其主轴转速控制并没有采用闭环控制方式，主轴转速存在一个小范围波动，傅里叶变换去除偏心的方法效果并不理想。因此本文提出一种最佳正弦拟合的方式去除偏心，基于整个测量周期拟合出最贴近实测曲线的正弦曲线，如图4 所示。这种测试方式可以在考虑转速波动的情况，得到最佳的偏心去除效果。

2.2 去除干扰信号

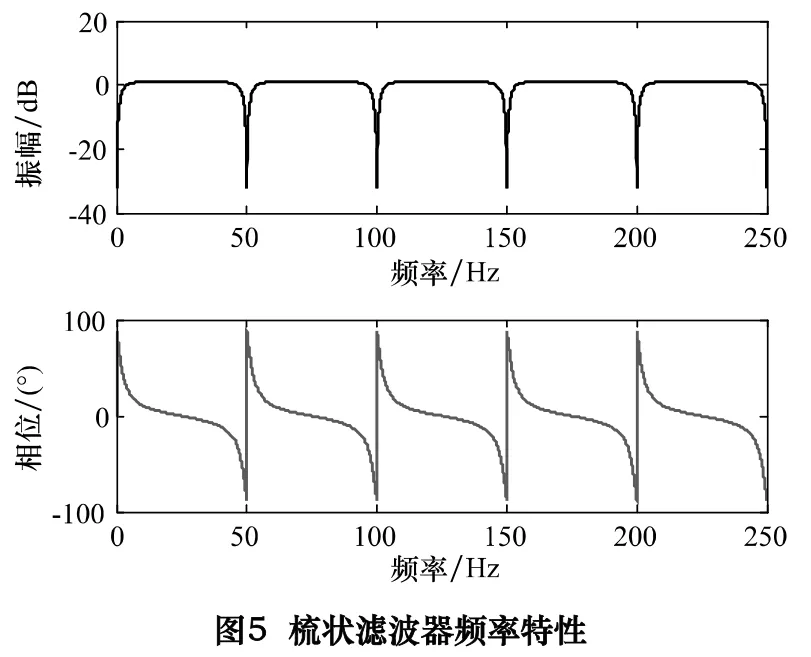
测试过程中不可避免地会引入工频干扰等，在纳米级测试中工频干扰是一个不可忽略的干扰源，如果对工频干扰处理不进行有效处理，甚至会在测量结果中引入微米级误差，这是绝对不能允许的。首先在测试时必须将电容传感器外壳和被测标准球杆共地，并对测得的信号进行滤波数据处理，本文采用梳状滤波器对信号中的工频干扰进行滤波，梳状滤波器频率特性如图5。

2.3 同步、异步误差分离

根据美国ASME(American Society of Mechanical Engineers)标准［12］，可以对主轴误差按照频率划分为同步误差和异步误差。同步误差又叫平均误差，指主轴回转基频整倍数的那些分量的总和;异步误差又叫随机误差，是指总误差减掉同步误差的剩余分量，包括主轴回转基频整数倍以外的其他误差成分以及基频以内的周期性谐波成分。这种分离方式对于工程评价和误差源辨识是具有实际意义的。同步误差往往对应于加工表面的周期性低频波纹误差，而异步误差则更多造成加工表面的高频粗糙度误差。研究中使用梳状滤波器，设置合理的滤波参数对信号中的同步异步信号进行提取分离。

2.4 参数化指标评价

按照误差方向分为轴向误差和径向误差，并分别进行同步误差和异步误差评价，得到主轴参数化的评价指标，用以表征主轴的旋转精度。由上部和下部X、Y通道分别获得该位置的径向误差，Z通道获得轴向误差，上、下通道联合计算可以得到主轴轴线的偏摆误差。

由于最小二乘法计算主轴回转误差其结果具有唯一性，精度高，并有成熟的计算公式，故选用最小二乘法对主轴回转误差进行计算，并使用圆度图像法评价主轴回转误差。最小二乘法计算方法如下:

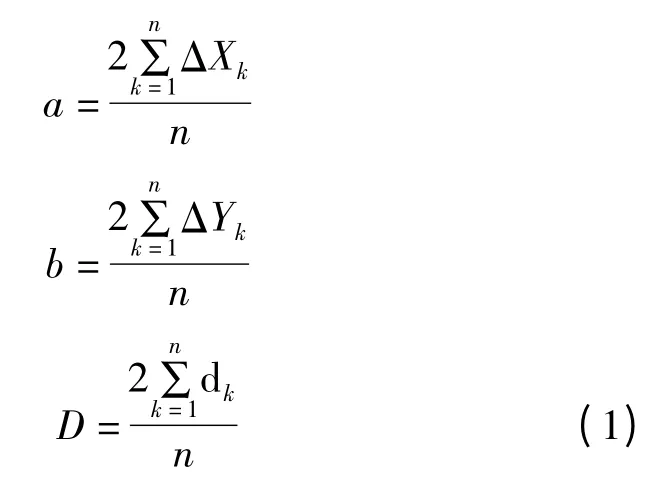
式中:a、b为最小二乘圆圆心坐标;dk为点(Xk，Yk)到坐标原点的径向距离。计算轮廓上各点到最小二乘圆圆心的距离为:

则主轴回转误差e计算如下:

根据以上的分析计算方法，使用ASME 主轴回转误差评价标准对主轴回转误差进行参数化评价。

由于圆度图像法可将主轴回转角度作为自变量，将采集到的位移按主轴回转角度叠加在基圆上，该法可以将复杂的主轴回转运动数据叠加在一个基圆上形成圆图像，从而可以直观地看出主轴的回转误差。故采用圆度图像法对主轴表示主轴回转误差。

2.5 全频谱分析模块

信号的频域图谱可以看出主轴回转误差的典型特征以及不同误差特征的影响程度。将采集到的不同转速的主轴回转位移数据全部进行傅里叶变换，并集中在一幅三维图上表示。这种显示方式对判断误差的来源和类别有很好的效果，能够对主轴的旋转精度做成综合性的评判。

3 测量实验与结果分析

3.1 测试数据的分析处理

根据上述算法对主轴误差数据进行分析处理，得到主轴不同方向的误差曲线和评价指标，并进行误差来源分析。

在转速390 r/min 下主轴回转误差计算圆度图像结果如图6、图7 所示，分别表征径向误差和轴向误差，并进行同步误差和异步误差分离，具体的误差值如表1 所示。

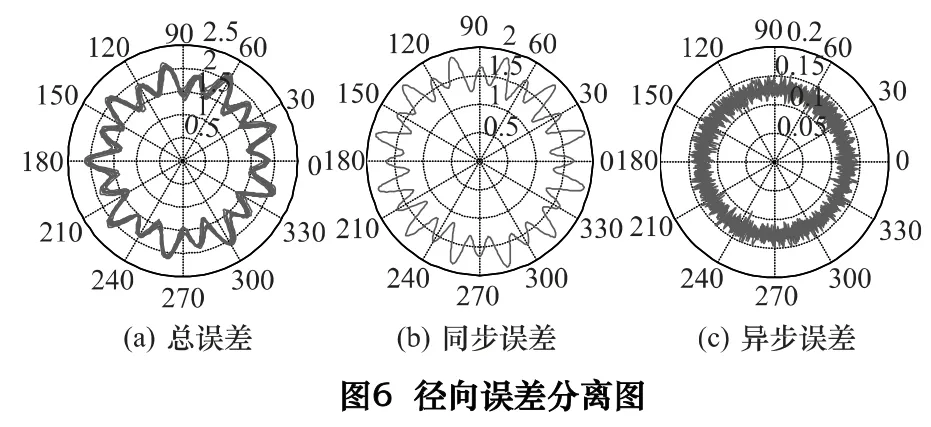
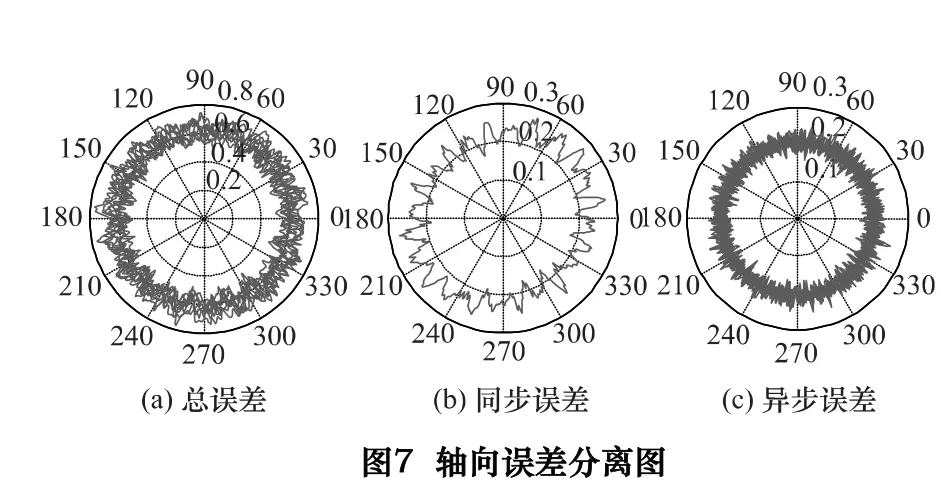
表1 主轴轴向误差与径向误差计算结果 nm

标准球杆和五通道电容位移传感器组成的系统，可以同步获得5 个通道的位移量，根据五通道数据可以唯一确定主轴轴线的运动规律，其中包含了轴向误差、径向误差以及偏摆误差的信息。以主轴轴线与刀具旋转圆平面的交点为起点，刀尖位置为终点，则这条线随主轴轴线旋转一周形成的圆端面如图8 所示。这幅图对于车削机床具有非常直观的意义，可以用来模拟车削后的端面面形特征。

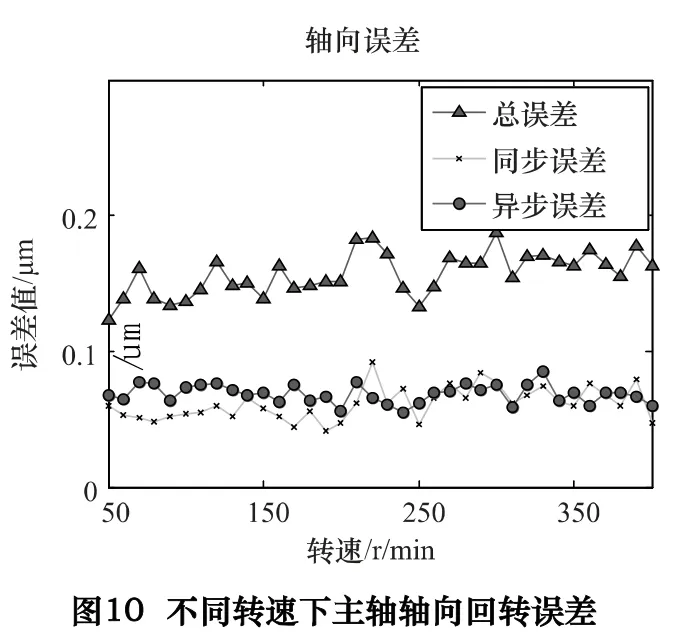
对不同转速下主轴回转误差数据进行计算，绘图表示不同转速下的各项误差指标如图9 和图10 所示。可以看出主轴转速在90、120、180、360 r/min 时各项误差值大幅增大，主要表现在径向误差方向。如果不考虑这4 个转速的影响，则在整个转速范围内，主轴径向总误差均小于500 nm，径向同步误差小于450 nm，径向异步误差小于80 nm，而轴向总误差小于200 nm，轴向同步和异步误差均小于80 nm。

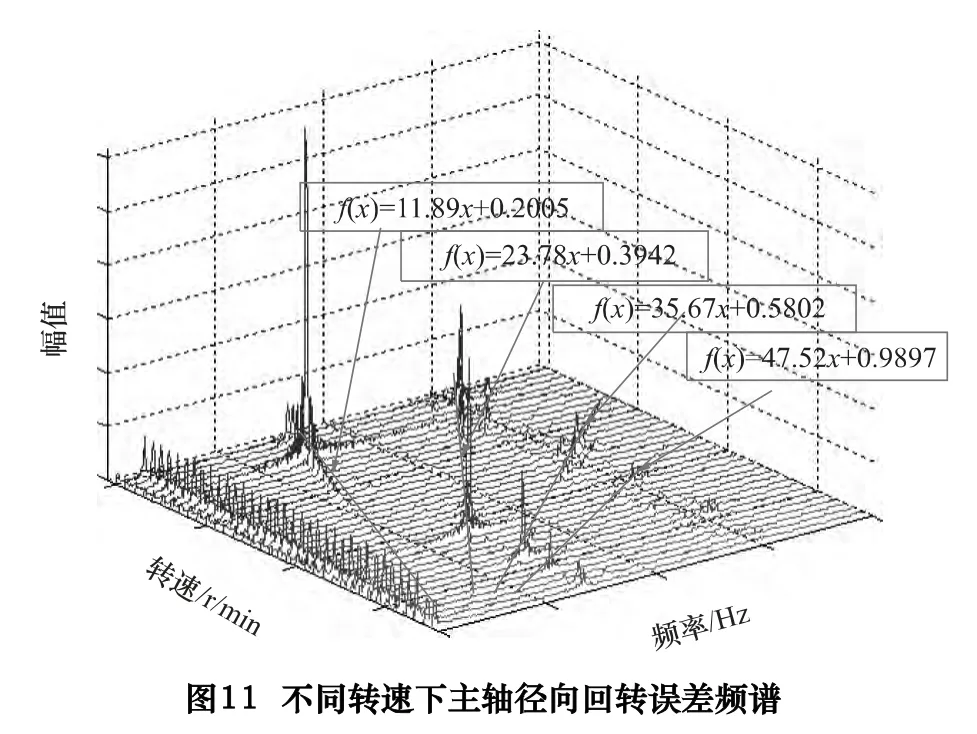
为分析以上4 个转速时误差变大原因，对不同转速径向回转误差做全频谱分析如图11 所示。发现当频率是转速的特定倍数时，误差会变大，体现在图上为4 条斜线，当这4 条斜线与72 Hz 和144 Hz 相交时，该频率处的误差陡然增大。对这4 条斜线进行线性拟合，其函数关系如下:

不难发现当主轴转速处于90、120、180、360 r/min时，恰好处于以上4 条斜线与72 Hz 的交点位置，机床加工时应尽量避免这些转速下工作。

3.2 典型误差对于加工表面的影响

根据上述实验现象，可以看出主轴旋转过程中存在一个与转速呈现12、24、36、48 倍频的线性规律，同时此四条斜线会引起机床某结构在72 Hz 处共振。

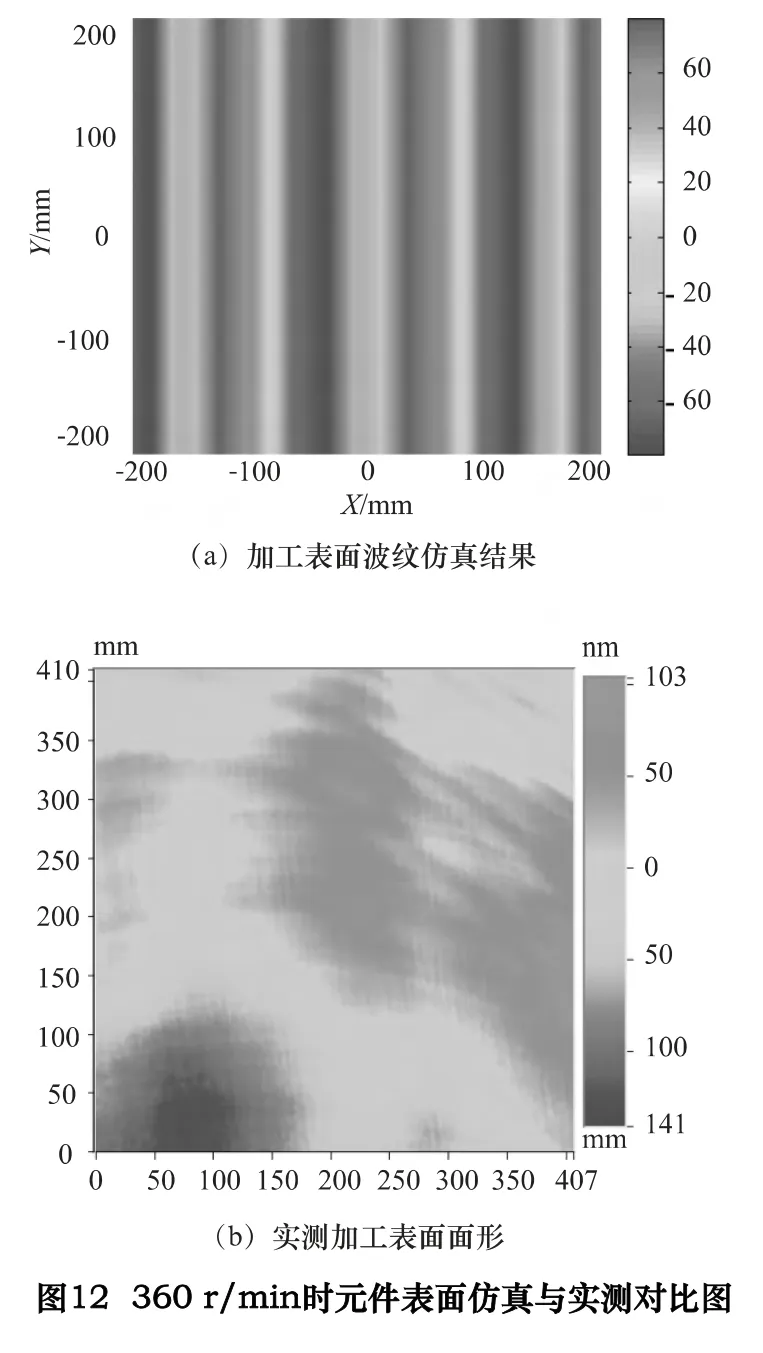
根据采集到的五通道位移数据，通过坐标转换得到刀尖运动规律，并仿真机床主轴在360 r/min 下加工大口径元件的面形如图12a 所示，其周期约为178 mm，幅值约为80 nm，而实际加工结果如图12b 所示，可以看出面形表面形貌特征是比较吻合的。因此在加工中需要避免在上述特定转速下运行，引起主轴回转精度恶化，从而导致加工表面出现异常波纹。考虑加工效率与主轴回转误差，在实际加工中使用390 r/min作为加工工艺参数是合理的。

4 结语

本文根据超精密机床主轴回转精度在线高精度测试的迫切需求，基于双标准球杆的五通道电容位移测试方法搭建了主轴回转精度在线测试平台。并对测试数据进行干扰抑制、有效数据提取和误差分离，得到了不同转速下的主轴回转精度指标。最终应用全频域分析模块研究主轴误差的分布规律，并提出需要规避的转速范围。通过对测试结果的分析表明:该机床主轴工作转速下(390 r/min)的径向同步误差为405 nm，径向异步误差为66 nm;轴向同步误差为59 nm，轴向异步误差为54 nm。另外，为避免机床主轴不正常振动，需要避开90 r/min、120 r/min、180 r/min、360 r/min 的转速范围。

［1］袁巨龙，张飞虎，戴一帆，等. 超精密加工领域科学技术发展研究［J］. 机械工程学报，2010，46(15):161 -177.

［2］安晨辉，王健，张飞虎，等.超精密飞刀切削加工表面中频微波产生机理［J］. 纳米技术与精密工程，2010，8(5):439 -446.

［3］徐志强，尹韶辉，陈逢军，等. 小口径非球面的超精密车削和抛光组合加工［J］. 纳米技术与精密工程，2013，11(6):479 -484.

［4］张文生，张飞虎，董申. 光学脆性材料的金刚石切削加工［J］. 光学精密工程，2003，11(2):139 -143.

［5］黄坤涛，房丰洲，官虎. 超精密车削表面微观形貌对光学特性的影响［J］. 光学精密工程，2013，21(1):101 -107.

［6］许乔，王健，马平，等. 先进光学制造技术进展［J］.强激光与粒子束. 2013，25(12):3098 -3015.

［7］夏欢，陶继忠. 空气静压球面轴承主轴回转精度测试研究［J］，轴承. 2013(7):56 -58.

［8］张丹，黄惟公，王瑞，等. 车床主轴回转精度数字式单向测量法［J］. 制造技术与机床，2014(10):41 -54.

［9］Bryan J B，Vanherck P. Unification of terminology concerning the error motion of axes of rotation［J］. CIRP Annals. 1975(8):555 -562.

［10］Donaldson R P. Simple method for separating spindle error from test ball roundness error［J］. CIRP Annals. 1972(2):125 -126.

［11］Gao W，Sato E，Onuma T. Roundness and spindle error measurement by angular three - probe method［J］. Journal of the Japan Society for Precision Engineering，2002，68(9):1195 -1199.

［12］ASME B89.3.4 -2010《Axes of Rotation:Methods for Specifying and Testing》