Nonlinear symbolic LFT model for UAV

TU Hai-feng(涂海峰), LIU Li(刘莉)

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)



Nonlinear symbolic LFT model for UAV

TU Hai-feng(涂海峰), LIU Li(刘莉)

(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China)

A nonlinear modeling framework is presented for an oceanographic unmanned aerial vehicle (UAV) by using symbolic modeling and linear fractional transformation (LFT) techniques . Consequently, an exact nonlinear symbolic LFT model of the UAV is derived in a standardM-ΔformwhereMrepresentsthenominal,known,partofthesystemandΔcontainsthetime-varying,uncertainandnonlinearcomponents.Theadvantagesoftheproposedmodelingapproacharethat:itnotonlyprovidesanidealstartingpointtoobtainvariousfinaldesign-orientedmodelsthroughsubsequentassumptionsandsimplifications,butalsoitfacilitatesthecontrolsystemanalysiswithmodelsofdifferentlevelsoffidelity/complexity.Furthermore,alinearizedsymbolicLFTmodeloftheUAVisproposedbasedontheLFTdifferentiation,whichisamenabledirectlytoasophisticatedlinearrobustcontrolstrategysuchasμ synthesis/analysis. Both of the derived LFT models are validated with the original nonlinear model in time domain. Simulation results show the effectiveness of the proposed algorithm.

nonlinear symbolic modeling; linear fractional transformation; unmanned aerial vehicle

Unmanned aerial vehicle (UAV) has received an increasing attention with their civil and military applications in recent years especially as low-cost UAV platforms[1].

A number of design challenges must be met as a result of the low-cost requirements. The reduced dimensions of the vehicles lead to highly nonlinear system behaviors and unconventional performance, which means that small UAV flight dynamics is less well understood than full size aircrafts. Furthermore, other indeterminacies like uncertain actuator responses, time delays, center of gravity shifts and mass variations also contribute to system uncertainties. Therefore, the design of a flight control law with adequate robustness plays a key role to compensate system against parameter variations.

The linear fractional transformation (LFT)[2]is introduced as a modeling framework associated with modern robust control methodology over the last twenty years. LFT is a special kind of representation for systems whose transfer behavior is assumed to be uncertain and/or varying. In this form the known or invariant parts, often abbreviated byM,areseparatedfromtheuncertainorvariablepartswhicharesummarizedandstackedtogetherinthesocalled“perturbation”matrixΔ.

Normally,LFTsarerestrictedtorepresentlinearsystemwiththeeaseofperformingstructuredsingularvaluetheoryforrobustnessassessment.However,itisstillnecessarytodevelophigh-fidelitynonlinearmodelswhicharecapableofcapturingallthecomplexityoftheplantforthefinalclosed-loopvalidation.Furthermore,aseriesofnonlineardesignsandanalysistechniquesareproducedmorerecentlybasedontheextensionoftraditionallinearapproachestoaddressnonlinearproblems,whichincludegainscheduling,linearparametervarying(LPV)[3]controlandintegralquadraticconstraintsamongothers.

Sincemanyoftheabovetechniquesworkwithmodelsbasedon,orsimilarto,theLFTmodelingparadigm,itisdesirabletodevelopasystematicnonlinearmodelingframeworkbasedonLFTrepresentations,whichofferstheflexibilityandmodularityrequiredtoobtainthesimplifiedmodelsusedforcontrollerdesign,butalsoconnectsthesemodelstotheoriginalandmorecomplexmodelsusedforcertification.RecentproposedanexactnonlinearLFTmodelingapproach[4]andaMATLABbasedtoolboxforLFTgeneration[5]havemadeitanattractiveandpossiblepropositioninaircraftdynamicsmodeling.

ThecontributionofthispaperisthatwedemonstrateasystematicprocedureofnonlinearLFTmodelingforanUAV.Basicstepsforthemodelingapproachareexplainedinmoredetails.TwospecialLFToperationsnamedLFTdifferentiationandnestedLFTsubstitutionarealsohighlighted,whicharenecessarytoperformafurthermanipulationofthenonlinearLFTmodel.Finally,theresultingLFTmodelsarevalidatedviacomparingthesimulationsoftheLFTmodelsintimedomainwithrespecttothatoftheoriginalnonlinearmodel.

1 Nonlinear symbolic LFT modeling approach

1.1 Definition of LFT

LetMbeap×qtransferfunctionmatrixandsupposetherearetwoappropriatelydimensionedblockstructuresΔuandΔlthatrelatetoMasshowninFig.1.SupposethismatrixMispartitionedas

(1)

The upper and lower LFTs are defined as

Fu(M,Δu)=M22+M21Δu(I-M11Δu)-1M12

Fl(M,Δl)=M11+M12Δl(I-M22Δl)-1M21

(2)

Assuming the inverse matrices exist, the LFTs will be called well defined.

An important characteristic of LFTs is that linear interconnection of basic LFTs can be grouped together into a single LFT.

Fig.1 Upper and lower LFT description

1.2 Modeling approach

The general framework of exact nonlinear modeling using symbolic LFT has been presented detailedly in Refs.[4,6]. The core idea is to transform the ordinary differential equations (ODEs) which define the nonlinear system into an exact nonlinear symbolic LFT form. In this manner, the structured ΔmatrixoftheLFTmodelcontainsthenonlinear,time-varyingoruncertaintermsassymbolicparameters.

AssumetheclassofnonlinearsystemsconsideredisdefinedbythefollowingODEs:

y=g(x,u)=g1(x)x+g2(x)u+g3(x)

(3)

wherex,u,yarerespectivelythestate,inputandoutputvectors,thenonlinearfunctionsfi(x), gi(x)aregivenbyapolynomialmixofanalyticexpressionsandtabulardata.Theonlyrequirementfortheclassofsystemsisthelineardependencyofthenonlinearfunctionsontheinputvectoru,whichisquitegeneralformechanicalsystems.Thebasicstepsofthemodelingapproachare:

①Useanonlinearstatespace2×2blockmatrixtorepresenttheODEs.Introducefictitioussignalsuf=1∀ttoincludethosenonlineartermsnotaffineontheinputsuorthestatesx:

(4)

②Definealltheuncertain,nonlinearandtimevaryingtermsassymbolicparametersρkanddenoteconstanttermsascj.Heren1, n2, nkindicatethenumberofrepetitionsforeachparameter.

(5)

③PerformthetransformationfromthenonlinearstatespacesymbolicmatrixtononlinearsymbolicLFTwhereallthesymbolicparametersareincludedintheΔ(ρ)matrix.Theessentialideaofthisstepisbasedonthesymbolicmatrixdecompositionalgorithm.

④FouradditionalstagescanbecarriedoutinordertomakeuseofdiagonalstructureofΔ(ρ)arisingfromthepreviousLFTmodelingprocess.Theyaresimplifications,modelreduction,approximationsanduncertaintycharacterization.

Then,amanageableLFTmodelfordesignandanalysisisobtained.Besidethepropertyofnaturalmodularityanddiagonalstructure,anotheradvantageoftheproposedmodelingapproachisthatitiseasilyconnectedwithothermodelsstemmingfromtheoriginalnonlinearsymbolicLFT,whichpreservestheusefulnessofestablisheddesignandanalysistechniques.Forinstance,linearmodelandLPVmodelcanbederivedfromthenonlinearLFTmodelbecausetheyareparticularcasesofthelatterandthen,correspondingdesignandanalysistheoriesareavailable.

2 UAV model description

Inthissection,agenericnonlinearmodelwhichcharacterizestheUAVflightdynamicsisdescribed[7].Theopen-loopnonlinearmodelcanberepresentedbythemainblocksofODEs[8],whichisillustratedinFig.2.

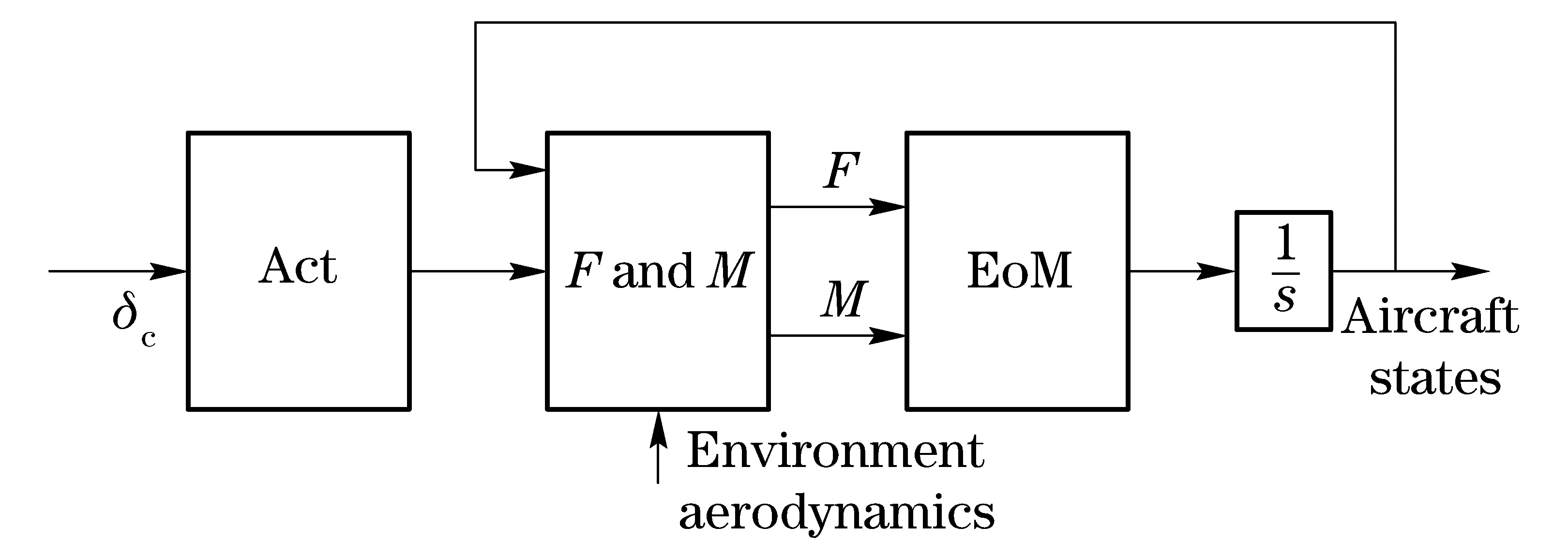
Fig.2 UAV model diagram

Inthediagram,EoMistheequationsofmotionblockwhichcomprisesthetwelvestandardaircraftstates.Theequationscanbewrittenas

(6)

whereFandMaretotalforcesandmomentswhichareconsideredastheinputsoftheEoMblock;V, Ω, Ξ, Ψarethelinearandangularrates,kinematicandnavigationstatesrespectively;TBHandTBEaretransformationmatricesfrombody-axestolocal-horizonandearth-frame;Iistheinertialmatrix; misthemassoftheaircraft.

Theinputsofthetotalforcesandmomentsblock,FandM,aretheaircraftstatefromEoMblock,theactuator(elevator,rudder,aileronandthrottle)deflectionandenvironmentandaerodynamicdata.Theoutputscanbeobtainedfromthefollowingexpressions

(7)

whereX,Y,Zrepresent aerodynamic forces in body-axes, andFeis engine thrust. The moments are given byM=FL, whereLis the proper moment-arm.

The avionics commands δcfromtheautopilotaretransformedintotheactuator(elevator,rudder,aileronandthrottle)deflectionδbytheactuatorsmodeledassecondordersystems

(8)

whereζatheactuatordampingratio, ωatheactuatornaturalfrequencyandsatdenotesthesaturationwhichisaddedinserieswiththeactuator.

OncethenonlinearUAVmodelinODEformisavailable,themodelingapproachproposedintheprevioussectioncanthenbeappliedtoobtainanexactnonlinearsymbolicLFTmodel,whichwillbeshowcasedinthenextsection.

3 LFT modeling of the UAV

3.1LongitudinalUAVmodel

Foreaseofdemonstration,onlyalongitudinalmodeloftheNOCUAVinthestabilityaxesisderived.

(9)

Theaerodynamiccoefficientsaredescribedas:

CD=CD0+CDαα+CDδeδe

(10)

3.2ExactnonlinearsymbolicLFT

AnexactnonlinearsymbolicLFToftheUAVisobtainedusingthefirstthreestepsfromsection2.2.Notethatalltheirrationalandtrigonometricalfunctionsshouldbeexpressedbyrationalexpressions.SincethelongitudinalmotionofUAVissomewhatsimple,itismoreconvenienttocombinetheFandMandEoMblockstogetherduringmodelingprocess.

Withrespecttostep1ofthemodelingapproach,itisdirecttowritetheODEsfortheUAVmotion(i.e.affineinthestatesandinputs):

(11)

where ρequalsto0.5SρairVforeaseofexpression.Animportantconsiderationinapplyingthemodelingframeworkistocovercomplexfunctionsbysinglesymbolicparameters.Hence, ρ1-ρ4areintroducedtoreplacethetrigonometricalfunctionswhereρ1=sin(α-θ), ρ2=cosα, ρ3=cos(α-θ)andρ4=sinα.Atthisstage,thesymbolicparametersareconsideredtobeindependentalthoughtheymaydependonasubsetofsamesystemvariables.SincewewillemploythestructuredtreedecompositionalgorithmwhichcanonlydealwithpolynomialobjectstoacquireLFTmodel,thereciprocalofairspeedVisconsideredalsoanewparameter.i.e. V-1= ρ5.

Thereduceddimensionsofthevehiclesleadtounconventionalperformance,asaresult,smallUAVflightaerodynamicsislesswellunderstoodthanfullsizeaircraft.Therefore,theerroroftheaerodynamicparametersshouldbetakenintoaccount.HerewechoosetheelevenaerodynamicparametersCD0-Cmδeasuncertainties.Intotal,twentytermsinthesystemaredeclaredassymbolicparametersincludingsystemstatesvaryingwithtime(V, α, θ, q),uncertainties(CD0-Cmδe)andtrigonometricalandirrationalreplacements(ρ1-ρ5).Remaindertermsareknownconstantsbecausetheyareinvariantwithrespecttotime.Withoutanylackofgenerality,thefourstatesareusedasoutputsofsystem.Inthiscase, g1(x)equalstoanidentitymatrixandg2(x)iszero.

Next,thenonlinearsymbolicmatricesinEq.(11)combinedwithg1(x)andg2(x)aretransformedintoanonlinearsymbolicLFTwhereallthesymbolicparametersareplacedintheΔ(ρ)matrixbasedonorder-reductionLFTalgorithms.ThetypicalobjectiveistofindaminimalrepresentationduringtheLFTmodelingsothattherepetitionsofthesymbolicparametersinΔ(ρ)areminimum,whichstillremainsanopenproblemdependingondifferentorderreductionmethodologies.Althoughtheproposedapproachisstraightforward,itsapplicationhasonlyrecentlybecomefeasibleduetothesoftwareimplementationofLFToperations.Thestructuredtreedecomposition[9]isusedherefortheLFTmodelingwiththeassistanceofLinearFractionalRepresentation(LFR)toolboxdevelopedatFrenchNationalAeronauticalResearchCenter(OfficeNationald’EtudesetdeRecherchesAérospatiales,ONERA)[5].Thestructuredtreedecompositionisageneralizationoftheideaconsistingoffactorizingsymbolicparameterssothattheyappearastheminimumtimesaspossiblebeforeproceedingtotherealization.

Afterperformingthetransformation,anexactnonlinearsymbolicLFToforder21with17symbolicparameters(CD0-Cmδe, V, ρ1-ρ5)isobtained.AttheexactLFTmodelingstage, αandθbothappearonlyinthetrigonometricalfunctionswhichhavealreadybeenreplacedbyρ1-ρ4,sotheyarenotincludedinthe17symbolicparameters. qdoesn’tshowupbecauseitsappearanceisoneandhasbeenputinthestatevector.

Theactuatorblockismodeledinthesamewayasabove.Thesaturationisconsideredasnonlinearityandalsoreplacedbyasymbolicparameterρ6.

3.3ApproximationsoftheexactLFTmodel

ItisobviousthatinΔ(ρ)oftheexactLFTmodel, ρ1-ρ4areartificialvariablesrepresentingcomplexfunctionsandhavenoexplicitphysicalmeaning.Actually,theyaredependentoneachotherbecauseeachofthemisafunctionofαandθ.Similarly, ρ5arereciprocalwithVandshouldbecovertbacktoV-1afterthestructuredtreedecomposition.Therefore,afurthermanipulationisdemandedtoreducethetotalnumberofindependentparametersinordertoreducetheconservativeness,whichmeanstheartificialparametersintheΔ(ρ)needtobereplacedbytheirexactexpressions(althoughitwouldtypicallyleadtoalargedimensionofthenewΔ(ρ)).TheresultingLFTmodelshouldonlycontainthenaturalsymbolicparametersofthesystem.ThisframeworkcouldbedoneeasilybytakingadvantageofthediagonalstructureofΔ(ρ).OnceaparameterinΔ(ρ)isapproximatedbyanewsymbolicexpression,thisnewexpressioncanbedirectlysubstitutedintothenonlinearsymbolicLFT.Moreover,theexpressioncanalsobeaLFT.Theideaisbasedonthefollowinglemma[6].

Lemma 1 Consider a lower LFT,y=Fl(M, Δ(ρ))uasshowninFig.3a.

Fig.3 Nested LFT

(12)

Byusingthislemma,theexactexpressionsofρ1-ρ5canbesubstitutedintothenonlinearsymbolicLFT.Asmentionedbefore,alltheirrationalandtrigonometricalfunctionsshouldbeexpressedbyrationalexpressions.Concerningthetrigonometricalfunctions,thefollowingTaylorseriescanbeapplied:

(13)

Thismeansthatαwillappear9timesforasinetermand12timesforacosineterm.

Aftertheapproximationandsubstitution,anonlinearsymbolicLFTwithorder48isobtainedfinally.ItisnotedthattheseapproximationtechniqueswillstillmaintainthenonlinearnatureandprecisionoftheLFTmodeliftheorderofTaylorseriesishighenough.

3.4Validationwithoriginalnonlinearmodel

Whencompletingtheentiremodelingframework,avalidationisrequiredontheresultingnonlinearsymbolicLFTmodelingwiththeoriginalnonlinearmodel.Here,anoceanographicobservationUAVisconsideredasexample.DuetothespecialstructureofthesymbolicLFT,aSimulinkbasedToolbox[10]developedbyONERAisutilizedforthehandlingofLFT.ThistoolboxprovidesaninterfacebetweentheLFRtoolboxandSimulinktofacilitatecomputingtheinterconnectionofdifferentLFTsfromLFRtoolboxandsimulatingtheLFTinSimulinkenvironment.Specialblockssuchasactuatorsaturationshavealsobeenaddedinthetoolbox.TheinterconnectionstructureoftheprobleminthispaperisshowninFig.4.

Fig.4 Simulink block for the symbolic LFT

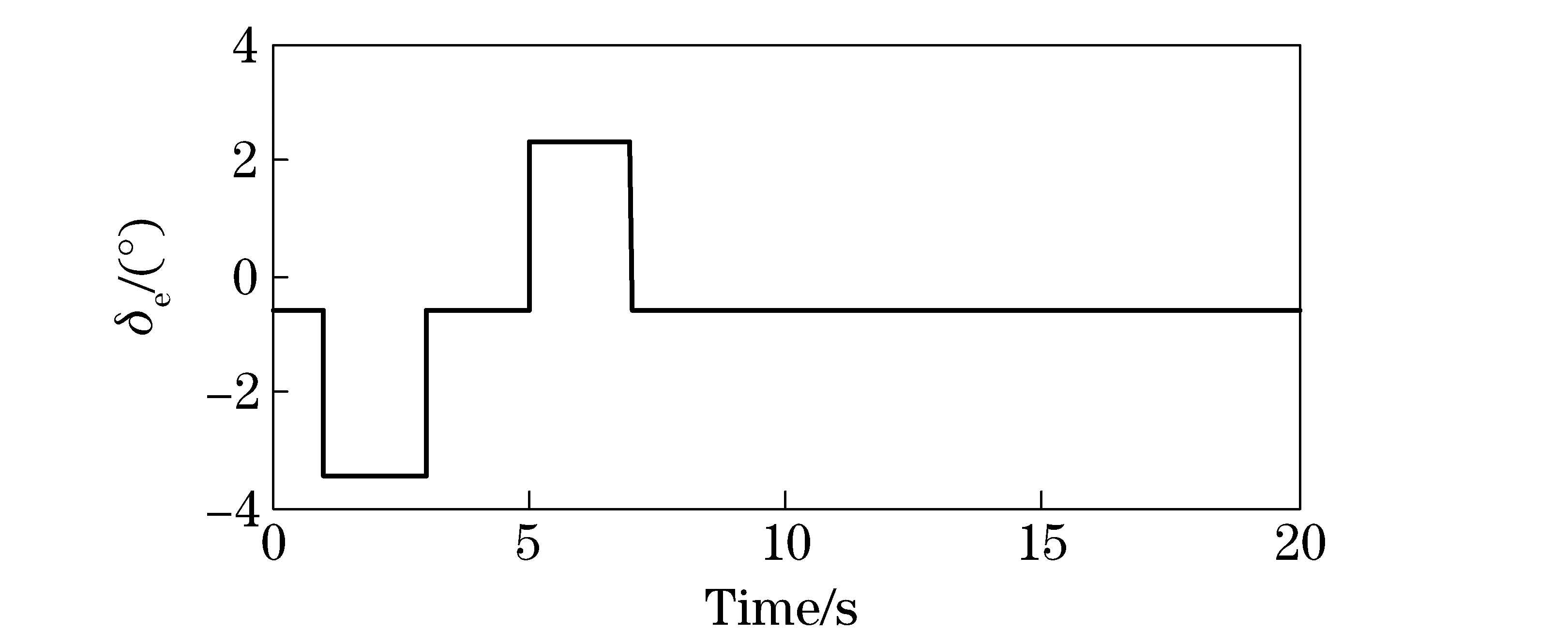
Fig.5 Maneuver input

ThesimLFR-ablockcombinedwith“parameters”blockisusedtosimulatetheUAVLFTmodel,theformerrepresentsMtermwhilethelattercoversΔmatrixintheLFT.SimilarlysimLFR-bblockisused,whichallowssaturationsincludedintheΔtosimulatetheactuatormodel.BeawarethatsimLFR-aandsimLFR-bblockscanalsobelumpedtogethertogenerateonenewLFTautomaticallybythistoolbox[11].ThesimulationofthenonlinearsymbolicLFTiscomparedtothatoftheoriginalnonlinearmodel(UAVand“actuator”blockinthefigure).Themaneuverisa±2.865°doubletelevatordeflectionasshowninFig.5.ThetimeresponsesaregiveninFig.6.

FromFig.6itcanobservedthatthetworesponsesarenearlyidentical,whichimpliesthesymbolicLFTframeworkisadequatetosimulateoranalyzeanonlinearsystem.

Fig.6 Time response of original and nonlinear LFT model

4 Linearized UAV model

Inordertouseasophisticatedlinearrobustcontrolstrategysuchasμ synthesis/analysis, a linear time invariant (LTI) LFT model of the system has to be obtained. The general approach is to symbolically linearize the original nonlinear system.

Write nonlinear model of the UAV as the following general form

y=g(x,u,p)

(14)

wherex,u,yare respectively the state, input and output vectors, andpis vector of varying parameters. These equations can be entered as symbolic objects in MATLAB using Symbolic Math Toolbox. Symbolic linearization is then performed at a given point of the equilibrium surface. We have

y=Cx0,u0,px+Dx0,u0,pu

(15)

wherex,y,udenote the variations with respect to the equilibrium values (x0,y0,u0). We have

(16)

ThentheLFTisperformedtoobtainthelinearLFTmodel[12-13].

AnalternativewaytoderivethelinearmodelwhichcombinesthelinearizationstepandtheLFTstepisusedherewiththeaidofLFRtoolbox.Inthisway,thenonlinearfunctionsinEq.(14)aredefinedasLFR-objectsoriginallyandthen,weexecutetheLFTdifferentiationtogetthefinallinearLFTmodel.Thefollowinglemmaisthebasictheoryofthisapproach[5].

Lemma 2 Let us consider a LFR-objectf

f=M21Δ(I-M11Δ)-1M12+M22

(17)

for some matrices (M11,M12,M21,M22). The matrix Δandthedifferentiationareasfollows

Δ=diag{δ1In1,δ2In2,…}

Hi=diag{0n1×n1,…,0(n1-1)×(n1-1),Ini,

0(n1+1)×(n1+1),…,}

(18)

After the LFT linearization, a linear LFT model is obtained. For the problem in this paper, only the aerodynamic parameters are considered as uncertainties in the linear model. Therefore, all other parameters including the states and inputs of the system are set to the trim value when finishing the LFT linearization. In order to apply μ synthesis/analysis, the uncertainties in Δmatrixshouldbenormalizedwithin[-1, 1].Finally,theresultinglinearLFTmodelisvalidatedwiththeoriginalnonlinearmodelintimedomain.Weusethenominalvalueoftheuncertaintiesinthesimulationtohaveafarecomparison.

Fig.7illustratesthatthelinearLFTmodelcanalmostcapturethecharacteristicsoftheoriginalnonlinearmodel,whichmeanstheproposedlinearizationmethodologyisfeasibleandtheresultinglinearmodelisreadyforthelinearrobustcontrol/analysis.

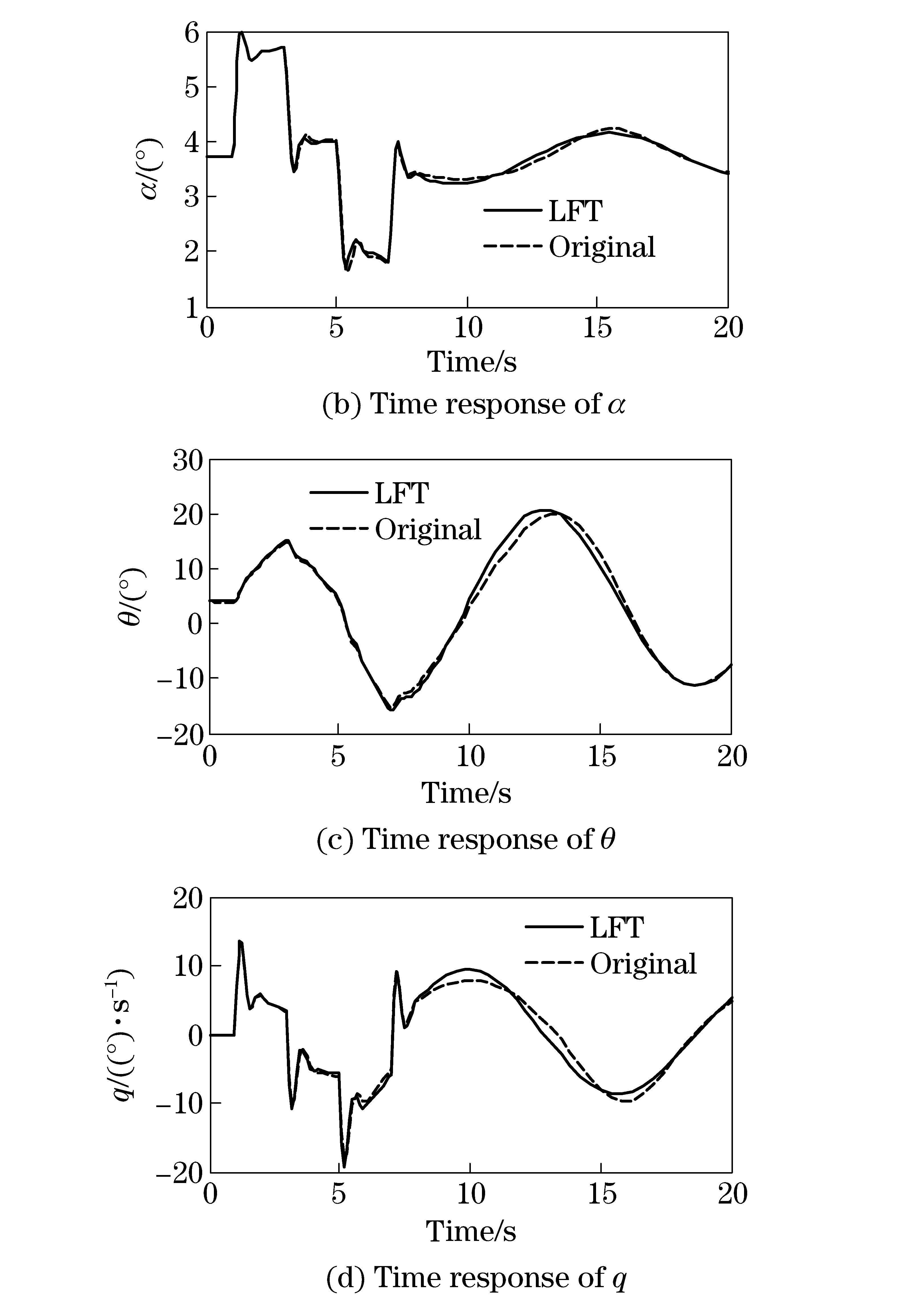
Fig.7 Time response of original and linear LFT model

5 Conclusion

InthispaperanonlinearmodelingframeworkispresentedforanoceanographicUAVbyusingsymbolicmodelingandLFTtechniques.Thismodelingapproachimprovesconsistency,continuityandconnectednessbetweenvariousmodelswhichstemfromthesamenonlinearsystem.Withahighlystructuredrepresentationofthesystem,theresultingnonlinearLFTmodelfacilitatesfurthermanipulationssuchasnestedsubstitutionandLFTdifferentiationinorderforthecontrollerdesignandanalysis.TwoMatlab/SimulinkbasedToolboxsareintroducedtomodelandsimulatethenonlinearsymbolicLFT.Attheendofthispaper,alinearizationmethodologyisstudiedtoobtainthedesign-orientedmodelsuitableforthelinearrobustcontrolstrategy.ThesimulationsofbothnonlinearandlinearLFTmodelintimedomainshowthattheproposedapproachisfeasibleandaccurate.

[1] Matthew Bannett. Development of technologies for low-cost oceanographic unmanned aeronautical vehicles[D]. Southampton: University of Southampton, 2008.

[2] Doyle J C, Packard A, Zhou K. Review on LFTs, LMIs, and μ[C]∥Proceedings of the 30th IEEE Conference, Brighton, 1991: 1227-1232.

[3] Marcos A, Balas G. Development of linear parameter varying models for aircraft[J]. Journal of Guidance Control and Dynamics, 2004, 27(2): 218-228.

[4] Marcos A, Bates D G, Postlethwaite I. Exact nonlinear modeling using symbolic linear fractional transformations[C]∥16th Triennial World Congress of International Federation of Automatic Control, Australia,2005: 190-195.

[5] Magni J F. Linear fractional representation toolbox (version 2.0) for use with Matlab[EB/OL]. [2013-08-20]. http:∥www.cert.fr/dcsd/idco/perso/Magni/.

[6] Marcos A, Bates D G, Postlethwaite I. Nonlinear symbolic LFT tools for modeling, analysis and design[J]. Lecture Notes in Control and Information Sciences, 2007,365:69-92.

[7] Li Meng. Development of modeling and control technologies for small UAV system[D]. Beijing: Beijing Institute of Technology, 2011. (in Chinese)

[8] Biannic J M, Marcos A, Bates D G, et al. Postlethwaite. Nonlinear LFT modeling for on-ground transport aircraft[J]. Lecture Notes in Control and Information Sciences, 2007,365:93-115.

[9] Magni J F. User manual of the linear fractional representation toolbox[R]. France: System Control and Flight Dynamics Department, 2006.

[10] Biannic J M, Doll C. Simulink handing of LFR object[EB/OL]. [2013-09-15]. http:∥www.cert.fr/dcsd/idco/ perso/Biannic/.

[11] Biannic J M, Doll C. Simulink-based tools for creating and simulating interconnected LFR objects[C]∥ IEEE Symposium on Computer-Aided Control System Design, Germany, 2006:1922-1927.

[12] Li Meng, Liu Li, Veres S M. Robustness assessment for flight control system of an oceanographic unmanned aerial vehicle[J]. Journal of Beijing Institute of Technology, 2011, 20(2): 158-167.

[13] Doll C, Berard C, Knauf A, et al. LFT modeling of the 2-DOF longitudinal nonlinear aircraft behavior[C]∥IEEE Int Symposium on Computer-Aided Control System Design, San Antonio, 2008: 864-869.

(Edited by Wang Yuxia)

10.15918/j.jbit1004- 0579.201524.0201

TP 273 Document code: A Article ID: 1004- 0579(2015)02- 0143- 08

Received 2013- 11- 27

E-mail: tuhaifeng86@126.com