Study on influencing factors of adapters separating with the underwater missile
FU De-bin(傅德彬), NIU Qing-lin(牛青林), LIU Xiao-jun(刘小军),LI Xia(李霞)
(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 10081, China)
Study on influencing factors of adapters separating with the underwater missile
FU De-bin(傅德彬), NIU Qing-lin(牛青林), LIU Xiao-jun(刘小军),LI Xia(李霞)
(School of Aerospace Engineering, Beijing Institute of Technology, Beijing 10081, China)
To analyze main factors affecting the separation reliability between a missile and adapters for the launching process, a six DOF underwater dynamic model for the missile and adapters is utilized to simulate the separation process, considering elastic forces of separating springs, hydrodynamic forces, gravity and buoyancy. Moreover, a criterion based on the maximum separating distance is put forward to determine whether adapters separate with the missile reliably. The results show that the magnitude and position of elastic force, the wedge angle and mass of the adapter significantly affect the separating process. The local sensitivity analysis for the reference status of design parameters demonstrates that the wedge angle of adapters has the maximum influence about 70.4% on the separating distance.
adapter; hydrodynamic force; separating spring; reliability criterion
Adapters have been found an increasingly wide utilization in the field of missile launcher, where the missile need to be kept smooth and steady over the bumpiest road and be sealed in storage by adapters. Besides, adapters give an orientation to a missile in radical direction and reduce the initial disturbance effectively to ensure success in launching. Although amount of studies on adapters have been carried out for the structural design and strength analysis[1-3], the separating reliability and main factors for a missile and adapters were investigated rarely, especially for the missile launching underwater. Therefore, it is necessary to investigate the separation process for the sub-marine missile launching.
Although few literatures considered the separating process of adapters for missile launching underwater, these papers also gave some valuable references. For example, Wang et al.[4]proposed a separating model, which regarded an adapter as a 6 degree-of-freedom (6-DOF) rigid body irrespective of force analysis, and a failure criterion. Gao et al.[5]researched on the influence on adapters’ separating action with different locations and velocities by ADAMS. The separating action of the adapter was studied in air environment in both the above-referred papers. Li et al.[6]reached a conclusion that the falling in depth leads to an increase of the cavitation number and the force loading on adapters, but a decline of the cavitation effect.
The present work focuses on the adapter separating process and main influence factors for a missile underwater launching process. The dynamics and kinematics model are established depending on external forces acting on the adapter, including gravitation, buoyancy, separating spring force, fluid drag and added mass produced by the attached water. Based on the separating model, some key parameters, such as elastic coefficient of the separating spring, the wedge angle, the position of the spring force acting on the adapter and adapter mass, are simulated to analyze how to affect the separation process.
1 Mathematic model
Adapters get moving with the missile before they overran the exit of the launching tube, when the separating spring is in compression and makes a pin rest against the surface of the missile, thus the spring force may work as soon as the adapter takes off the tube. A typical structure of the adapter is shown in Ref.[1]. The wedge surface can produce complex forces in the solid-liquid coupling region. Then the adapter can be separated with the missile successfully.
1.1 Coordinate system and motion parameters
There are 6-DOF reference frames to describe the adapter’s motion underwater including adapter body-fixed coordinate system (O-x1y1z1), fixed coordinate system (A-xyz), velocity coordinate system and ballistic coordinate system (O-x2y2z2), missile body-fixed coordinate system (Od-xdydzd), as shown in Fig.1[7].
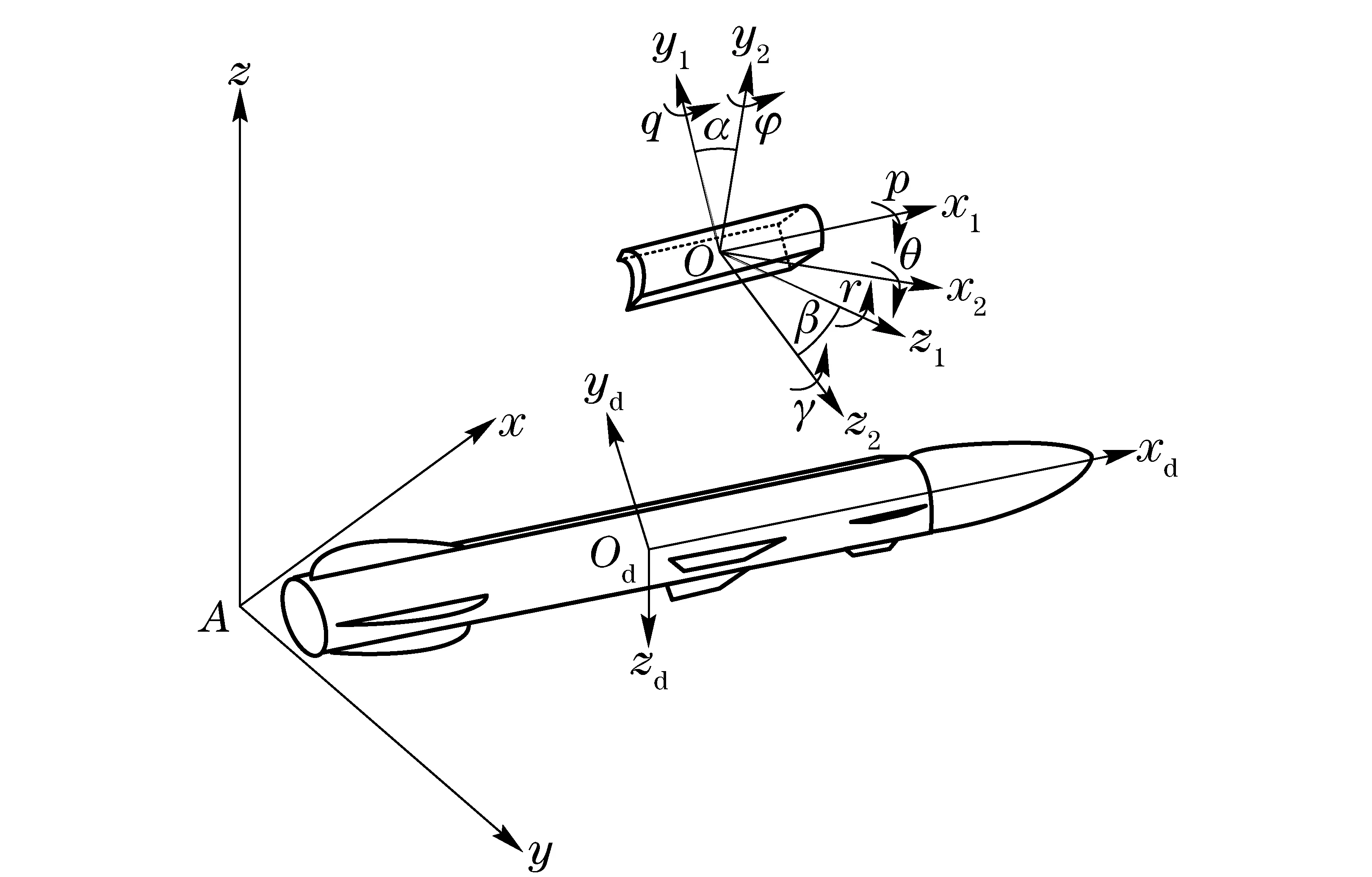
Fig.1 Coordinate system
To establish the mathematic model of adapter motion, forces are analyzed in adapter body-fixed coordinate system, and moments in ballistic coordinate system. The motion parameters of the adapter are defined as follows.
① Force and linear velocity inO-x2y2z2
F2=G2+Q2+N2+H2, V2=[u,v,w]T
② Moment parameter inO-x1y1z1
M1=MG1+MQ1+MN1+MH1
③ Position parameters inA-xyz
Pa=[x,y,z]T,Pd=[xd,yd,zd]T
④ Angular velocities ofO-x1y1z1andO-x2y2z2relative toA-xyz
Ω=[θ,φ,γ]T,ω=[p,q,r]T
where G, Q, N, H present the gravity, buoyancy, separating spring force and hydrodynamic force;u,v,wexpress velocity components inO-x2y2z2. The subscript 1, 2 and non-subscript refer to the conditions inO-x1y1z1,O-x2y2z2andA-xyzrespectively, and a to adaper and d to missile.
1.2 Separating spring force
One endpoint of the separating spring fixes to the adapter and its position inO-x1y1z1is described as Pa1. The other, pressing itself against the surface of missile, keeps the same velocity with the missile and its position inOd-xdydzdis Pad. The position vector of the separating spring inA-xyzis expressed as
(1)
(2)
Then the separating spring force and moment applying on the adapter are expressed as
(3)
(4)
1.3 Hydrodynamic force
Considering the influence of wedge surface, the hydrodynamic force is expressed as the sum of hydrodynamic drag force and the wedge surface force.
H=Hd+Hw
(5)
Omitting the cavitations’ effect, the hydrodynamic force is directly proportional to the square of the relative velocity[8]. The hydrodynamic drag force can be obtained depending on an appropriate drag coefficientCdas follows
(6)
(7)
whereρ0is the density of water,Sx,Sy,Szare the cross-sectional areas andVx1,Vy1,Vz1are the velocities of the adapter inx1,y1andz1direction respectively.
Similarly, the hydrodynamic moment can be expressed as
(8)
where the upper and lower limit functions of integral refer to geometric boundaries which can describe the shape of the adapter. For a simple but realistic method of calculation, the viscous resistance between the fluid and solid surfaces is neglected.
Based on this method, the influence of wedge surface of the adapter is considered as follows. Fig.2 shows the profile of the adapter, where a coordinate systemητnis established. The force of thendirection is given as
(9)
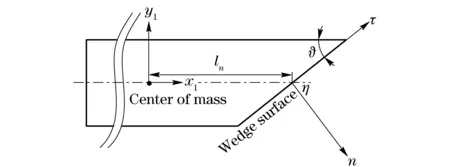
Fig.2 Wedge surface profile of the adapter
Thus the drag and addition moment inO-x1y1z1can be shown as
(10)
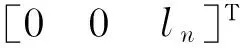
(11)
whereSwis the cross-sectional area of the wedge surface, ϑ is the angle of the wedge,lnis the arm of the force inndirection.
Without considering the compressibility of fluid, the added mass of structure in fluid environment is only determined by the geometric shape instead of flow fields[9]. Kinetic energy of the planar irrotational flow with ideal incompressible fluid, where outer boundaries of flow fields locate at infinity, can be obtained by area theorem[10].
(12)
Theflowfieldswithcomplexpotentialisdescribedbyanequivalenttransformationwithanelliptic,andthenthecomplexpotentialontheξplane is used as
(13)
(14)
Accordingtotheaboveformula,theaddedmassofadapterisgivenas
(15)
wherea,b,care equivalent structure dimensions.
感冒90%以上是由病毒感染引起的,一般7天左右可以自愈。宝宝得了感冒,爸爸妈妈做好居家护理很重要,下面让我们看看医生给爸爸妈妈的这些居家护理建议吧。
1.4 Dynamics and kinematics model
Based on the momentum theorem, the translational and rotational dynamic motion equations of the adapter in the moving coordinate system can be described as follows
(16)
(17)
whereH=(J′+J)Ω,mais the adapter mass andm′is added mass correspondingly, J and J′ are the matrices of rotational inertia and added mass, H is the moment of momentum,δis the differential symbol in ballistic coordinate system.
The missile keeps translation during moving in the launching tube. By omitting its added mass, the dynamic motion equations of missile is given as
(18)
Consideringtherelationshipbetweenadapterpositionandattitude,thelinearandangularvelocitiesinthefixedcoordinatesystemcanbegivenas
(19)
whereVis the value ofV2,θ0andφ0are trajectory inclination angle and magnetic declination angle respectively.
1.5 Separating reliability criterion
To ensure the reliability of the separating action, the adapter never contacts with the missile body and its wings throughout the separating action are put forward as a failure criterion. Obviously, whether the trajectory path of the most dangerous point of the adapter intersects with that of missile is noteworthy, as shown in Fig.3. The mathematical description of reliability criterion is expressed as
hmax-hw-r>0
(20)
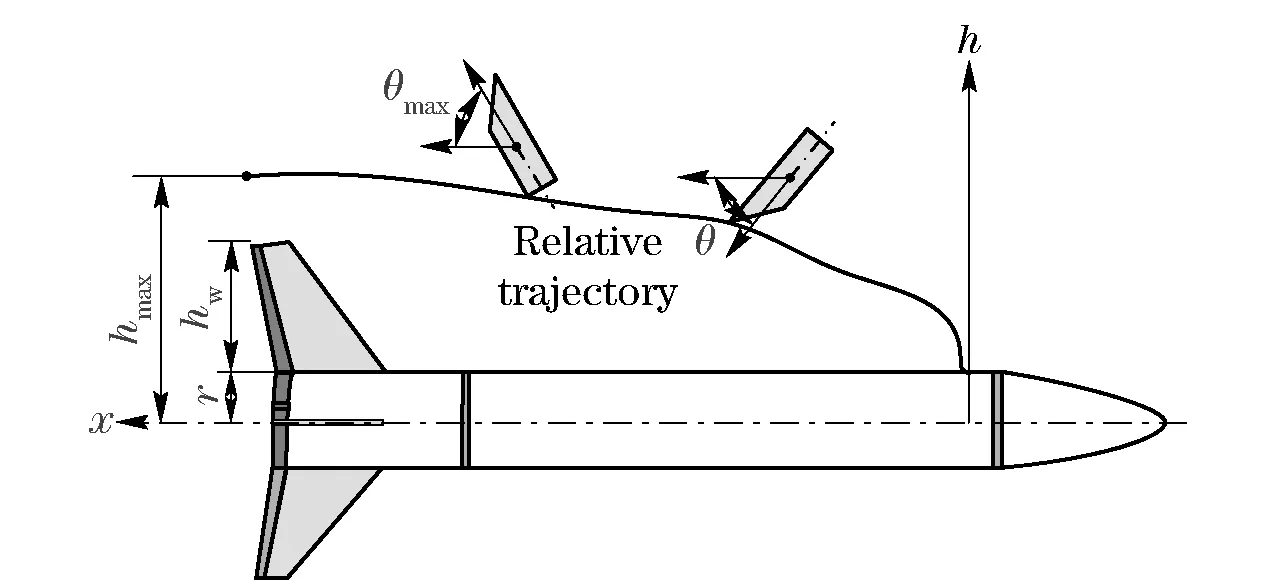
Fig.3 Profile of the trajectory
2 Simulation and discussion
2.1 Establishment of simulation
In accordance with the characteristics of the missile and its adapters shape, some items may be simplified in above equations. Generally, the motion of the adapter is in a vertical plane because of the symmetrical structure. Then the equations in the vertical plane are solved by employing the four-order Runge-Kutta integration method with constant step.
The initial parameters for a torpedo tube launching, as a sample to investigate the separating process, are shown in Tab.1, wherer,hw,landPare radius, wings height, length and thrust of the missile,handLare height and length of the adapter,X0is the initial length of the separating spring,LASis the distance from Pa1to O,LAdis the distance from O to Od. With the missile initial velocity asv0=20 m/s, four items are considered as shown in Tab.2, and some typical results, such as maximum heighthmax, maximum angular velocityωmax, maximum angularθmax, contact time of the spring and the adaptertcare discussed in the next section. These quantities are non-dimensionalized with respect to appropriate reference values,hmaxwithhw,wmaxwithφref=10 rad/s,θmaxwithψref=1 rad,tcwithtref=100 s.

Tab.1 Initial parameters of a simulation example

Tab.2 Values of parameters for different items
2.2 Results and discussion
With variations of elastic coefficients for separating spring from 0.01 to 10 kN/m, the typical result curves are shown in Fig.4. It can be seen that bothhmaxandθmaxincrease firstly and then decrease with the increase of elastic coefficients. The adapter contacts with the missile body inK<2 kN/m and collides with the wing inK>10 kN/m. An appropriate value of elastic coefficient,K=6 kN/min this example, has higherhmaxand lowerθmax. The curves ofωmaxandtcshow the trend of monotone decreasing.

Fig.4 Characteristic curves of the motion related to elasticity coefficient of separating spring

Fig.5 Characteristic curves of the motion related to wedge angle
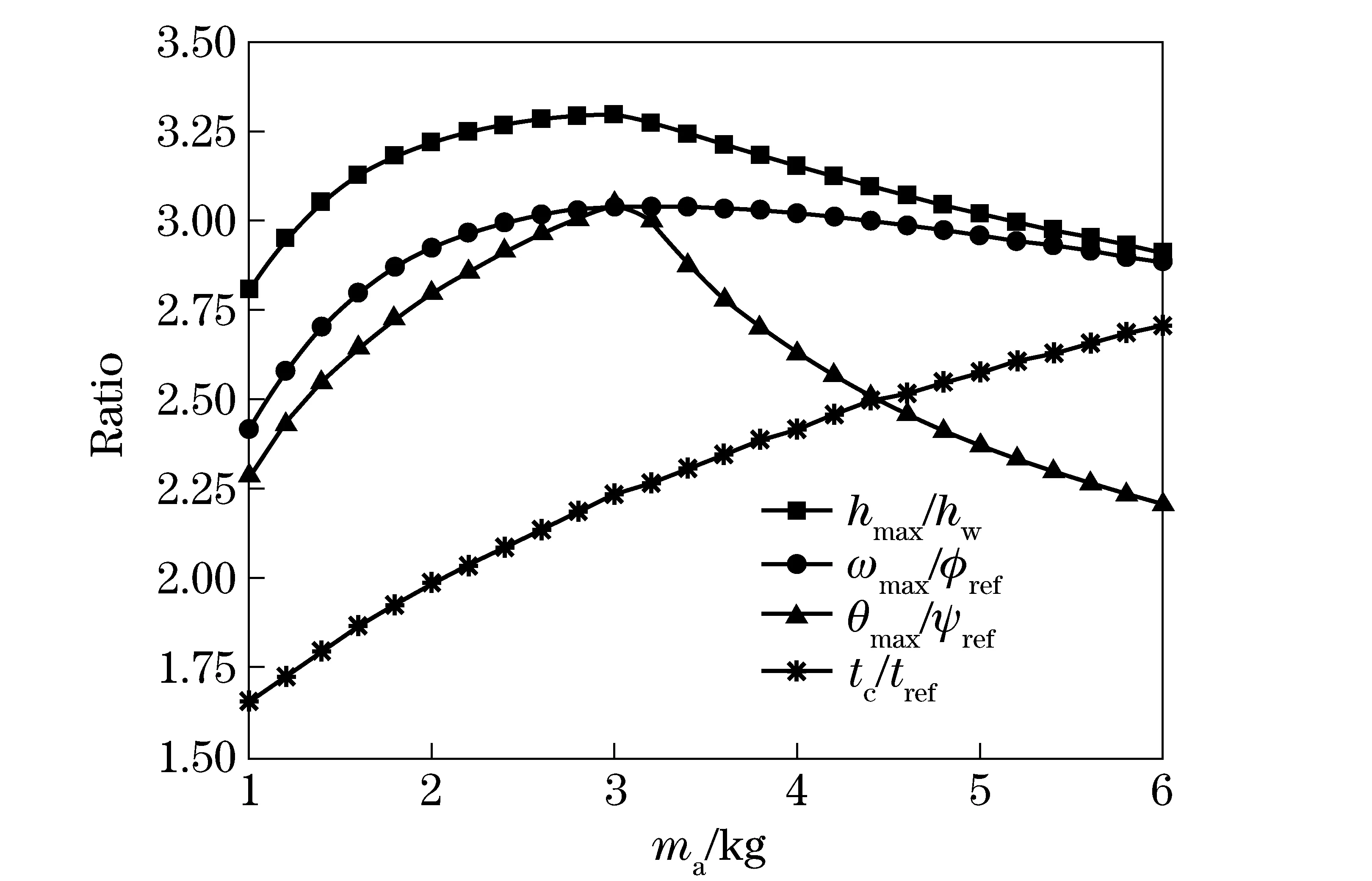
Fig.5 shows characteristic curves of the adapter motion related to wedge angle, with three curves displaying irregular parabola shapes. The adapter cannot separate with the missile other than 30°≤ϑ≤75° because ofhmax Fig.6 shows thatLAShas very little effect on the behavior of adapter in an appropriate range, namely -0.1≤lAS/(L/2)≤0.55 in this simulation, where the adapter can reliably fly over the missile wing. However, it is sensitive beyond the scope, in which a minor change inLASproduces a drastic change in movement. Fig.6 Characteristic curves of the motion related to arm of elastic force acting on the adapter Fig.7 shows that all curves excepttcincrease drastically first and then decrease slightly, reaching peaks at the same horizontal ordinate. However,tcincreases with the increase of adapter mass. Forma<3 kg, the hydrodynamic force from the wedge surface increases because of the decrease of angular velocity, while a great mass means that a great inertial force can be produced, which makes the rate of angle change stable. Fig.7 Characteristic curves of the motion related to adapter mass A sensitivity analysis method is employed to describe the impact of these factors on the system. For a multi-variable functionS=f(x1,x2,…,xn), the variation ofScan be expressed by the increment in a variable as follows (21) (22) whereajis the polynomial coefficient,xiis theith parameter. Furthermore, a simple linear formula with the weighting factors at the reference point is given to clearly describe the influence of four key factors as (23) whereciis the weight coefficient, Δ is the symbol of the differential variable. According to this method, the wedge angle of adapters has the maximal influence about 70.4% on the separating distance at the reference point, followed by mass of the adapter about 21.7%. The weight coefficients of magnitude and position of elastic force are 3.7% and 4.2% respectively for the reference state. The dynamic equations are established for adapters separating process during missile’s underwater launchingprocess, considering the gravity,buoyancy, separating spring force and hydrodynamic forces. Based on this model, the separating process is simulated and some influential factors, such as the magnitude and position of separating spring force, angle of the wedge, and mass of the adapter, are discussed in details. Results show that the wedge angle of adapters has the maximal influence on the separating reliability for the given reference state. This provides references for engineering design in real underwater environments. [1] Zhao Shiping, Cai Timin. Effects of lateral flow to the missile vertical launched from a submarine [J]. Journal of Ship Mechanics, 2006, 10(4):34-37. (in Chinese) [2] Zhao Hua, Wang Minjie, Yang Wei, et al. Adapters for canister-launched missile [J]. Tactical Missile Technology, 2007(4): 42- 50.(in Chinese) [3] Li Shijun, Le Guigao, Lin Guowen. The research on interference fit between missile adapter and launch canister [J]. Engineering Mechanics, 2011, 28(4):245-250.(in Chinese) [4] Wang Yunfei, Zhang Jianguo. Reliability analysis and calculation of the missile and adapter’s separating action [J]. Acta Aeronautic Et Astronautic Sinica, 2003, 24(4):297-299. (in Chinese) [5] Gao Qiang, Bai Jing, Zhang Ping,et al. Research on influence of reaction-force at different location and wind speeds on adapter’s separating action [J]. Missiles and Space Vehicles, 2013, (3): 23-26.(in Chinese) [6] Li Chao, Wang Hanping, Feng Jianxiang. Simulation of dynamic characteristics in cavitations flow for adapter based on FLUENT [J]. Journal of the Academy of Equipment Command & Technology, 2010, 21(3):93-95.(in Chinese) [7] Qian Xingfang, Lin Ruixiong, Zhao Yanan. Dynamics of flight for missiles [M].Beijing: Beijing Institute of Technology Press, 2011.(in Chinese) [8] Zhang Mingyuan. Fluid mechanics [M]. Beijing: Higher Education Press, 2010: 266-267.(in Chinese) [9] Wang Jisheng, Yang Qingshan. Calculation on added mass of structures in fluid environments [J]. Journal of Northern Jiaotong University, 2003, 27(1):41-43.(in Chinese) [10] Milne L M. Theoretical hydrodynamics [M]. London: MacMillan Co. Ltd, 1968:200-240. (Edited by Wang Yuxia) 10.15918/j.jbit1004- 0579.201524.0203 V 41 Document code: A Article ID: 1004- 0579(2015)02- 0158- 06 Received 2013- 09- 03 E-mail: fdb007@bit.edu.cn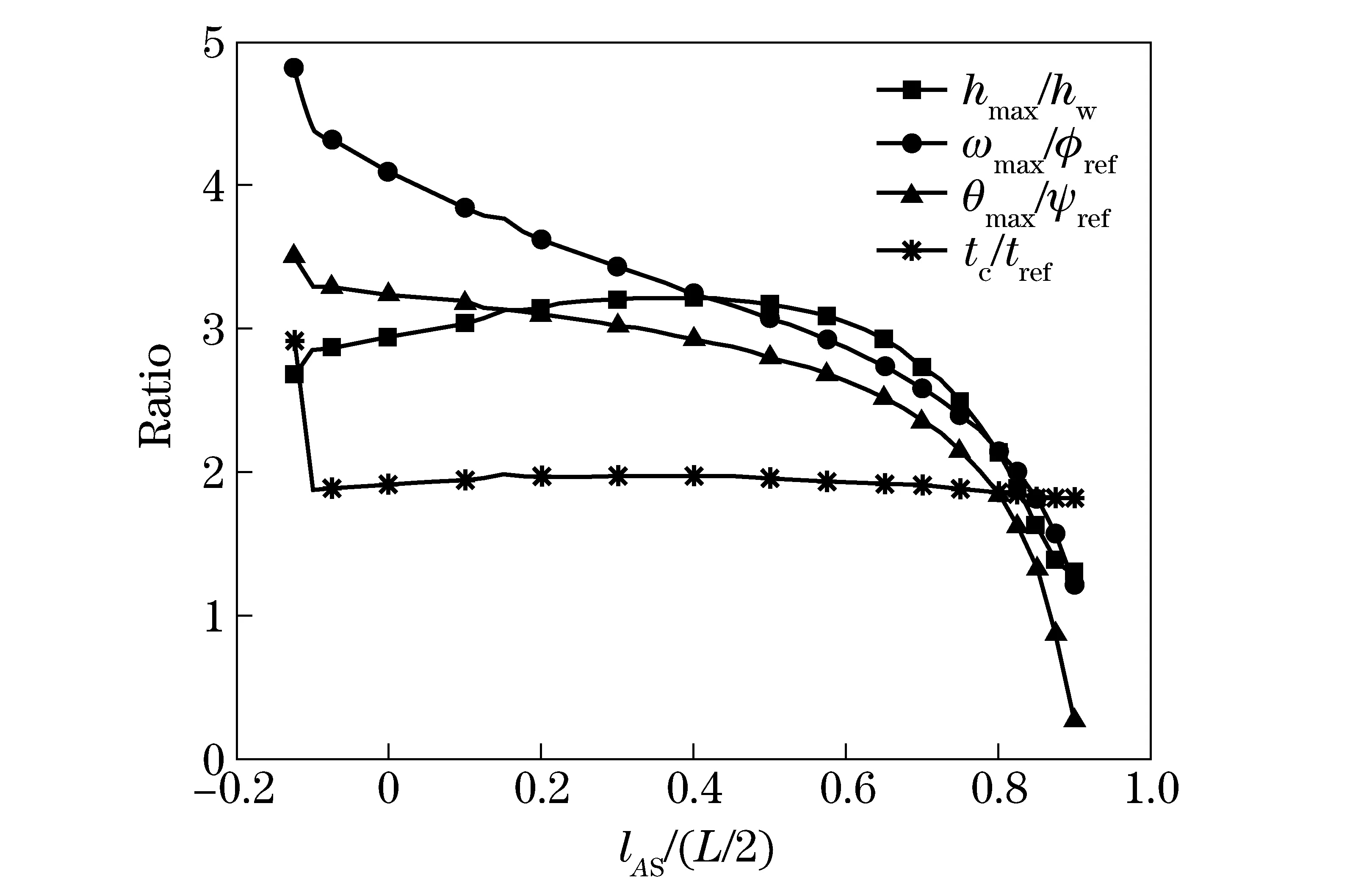
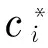
3 Conclusion
 Journal of Beijing Institute of Technology2015年2期
Journal of Beijing Institute of Technology2015年2期
- Journal of Beijing Institute of Technology的其它文章
- Nonlinear symbolic LFT model for UAV
- Novel scheme of high precision inertial measurement for high-speed rotating carriers
- Fast-solving method for air-to-surface guided bombs’ allowable attack area
- Design and analysis of mechanical self-destruction and self-neutralization mechanism for submunition fuze
- Resilience approach for heterogeneous distributed networked unmanned weapon systems
- Modeling and simulation of the static characteristics of diaphragm spring clutches
