Fast-solving method for air-to-surface guided bombs’ allowable attack area
LI Qiang(李强), XIA Qun-li(夏群利), CUI Ying-ying(崔莹莹)
(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Ordnance Science Institute of China, Beijing 100089, China)
Fast-solving method for air-to-surface guided bombs’ allowable attack area
LI Qiang(李强), XIA Qun-li(夏群利)1, CUI Ying-ying(崔莹莹)2
(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.Ordnance Science Institute of China, Beijing 100089, China)
A new method called local accurate search is put forward to calculate the allowable area for air-to-surface missiles based on the conventional methods. Comparing with traditional methods, the local accurate search method can search the area online and reduce the time of search with the required precision. Combining the traditional flight range table with a model calculation method, the new method employs the local search to find an accurate result, which will meet the fast-calculation requirements for attacking moving targets. In this way, the missiles are adapted for the complex warfare situation.
control technology of aircraft; allowable attack area; fast calculation; search online
Air-to-surface precision guided bombs including flighter bombers are used for precision attack to surface targets as buildings, bridges, radar stations, air defense command centers etc. Precisely allowable attack range calculation and shorter emission reaction time are important combat ability requirements of the weapon system, and the aircraft allowable attack range calculation is an important issue. Allowable attack range under the current location of aircraft and target information is transferred to an airborne computer. With the target entering into the allowable currently attack range of aircraft; airborne computer informs the fire control system to attack the target by the bombs. Working procedure of airborne weapon is shown in Fig.1.

Fig.1 Working procedure of airborne weapons
Method of bombs release calculation system is an important influence factor of attack area. Traditional methods include curve-fitting and model calculation[1]. The advantage of curve-fitting calculation is fast. But calculation accuracy is related to data of the firing table. To ensure its calculation precision, mass model data needs to be stored by the airborne computer, without considering influence of attack area from target moving[2]. The advantage of model calculation is that it is solved on line, mass-data are not needed to store, and precision is often high. But it takes more time to calculate. A new method called local accurate search is put forward through a reasonable simplified mathematical model combining curve-fitting with a model calculation method. It can adapt to various campaign environments on the result precision and calculation speed.
1 Mathematical modeling
1.1 Mathematical model for missile
The missile is regarded as a controllable particle based on the demand of real-time calculation, reason-able hypothesis and simplification. The 3-DOF mathematical model is established in Ref.[3].
1.2 Model for guidance and control
The target is regarded as a particle. A guidance law model is built based on missile-target relations[4].
qyaw=tan-1(-z1/x1)
(1)
(2)
(3)
(4)
Longitudinalandlateralguidanceusetheproportionalguidancelaw.Accelerationcommandsarelistedasfollows:
(5)
(6)

There are some model errors on acceleration commands tracking. Introducing proper dynamic lag to the control circuit is necessary. The control circuit is a high order system usually made up of actuators, elastic and inertial devices. It includes several time constants, but one proper equivalent time constant is considered to achieve the relatively accurate model[5]. Considering lag effect on acceleration command transferring, the first-order kinetics function[6]is added.
(7)
Tis one order time constant. When the transfer model of high order system is known, the dominant pole is first confirmed, and then equivalent one order time constant is confirmed. However, most model descriptions are not acquired exactly, the equivalent time constant is defined as the time that the system achieve 63% of stable value by a step input[5]. This paper uses 63% stable value to confirm one order time constant, and lateral and longitudinal time constants are the same as Ref.[6].
By Eq.(7) the pitching channel and yaw channel acceleration commandayandazare to generated, and the aerodynamic coefficients are calculated by using acceleration commands. Then the attack angle and sideslip angle through aerodynamic data tables and flight Mach number are calculated. This paper presents a simplified particle model comparing with six degrees freedom model of vertical acceleration contrastive curve shown in Fig.2.

Fig.2 Comparison of vertical overload
2 Attack area solving method
The boundary of attack area is obtained by the current position of the aircraft to calculate the impact point. Appointing the virtual target position and calculating the miss distance is the first step. If miss distance meets the performance indicators, constantly updating the virtual target position. The boundary of attack area is confirmed until the miss distance does not meet the performance indicators. The problem can be summarized as solving the secondary nonlinear equation:f(x1,x2)=ε, that is, solving problems
minF(x)=min(ε-f(x))2
(8)
wheref(x) is the miss distance solution function, andx1 The optimal solution of the target function has two values based on the physical meaning of the attack area, the recent and far boundary. It is hard to get the two optimal solutions. And the solution efficiency is also low. Combining the quadratic problem with the specialty of the attack area, the problem can resolve two linear problems minF(e1+αp1)=minφ(α),α>0 minF(e2+αp2)=minφ(α),α>0 (9) wheree1,e2are the searching initials; p1, p2are the searching directions;φ(α) is the objective function of unique solution. Differentinitial values have significantly effects on the solving speed about one-dimensional searching problems. So the firing table under typical conditions is used. The recent and far boundaries are obtained by looking-up the firing table based on the current flight status. The above simplified trajectory model is used to optimize the solving program further. The process of local accurate search is shown in Fig.3[8]. Fig.3 Process of local accurate search 2.1 Reference launched scale Before the air-to-surface guided bombs are used, it needs to calculate the off-line model result under the typical launch condition. Initial attack area is treated as a firing table, and the data is put into the airborne computer when the airplane takes off, and used as the current flight state table. The initial value of the local accurate search is confirmed by the data. 2.2 Searching initial value correction The result of look-up scale based on the reference firing table only depends on height and speed of launching. To ensure continuity and singularity of the results, and considering the influence of the dive bombing, the pitching bombing, launching off-axis angle and the characteristics of target motion on the attack area, the result should be corrected. X0=X+φ(θ,ψV,VT) (10) whereXis the result in the scale;φis correction function;θis impact angle;ψVis the launching off-axis angle;VTis the target motion speed;X0is the local searching initial value. 2.3 Miss distance After confirming the search initial value, the searching direction of the boundary of allowable attack area is confirmed based on a simplified trajectory mathematical model for the local accurate search and comparing the target miss distance with the reference value. The calculation of miss distance has certain influence on the precision and efficiency of the local searching. This paper uses the calculation method of miss distance based on variable step length fixed. (11) wherehisX0search step;kis gain coefficient.xT,zTare target locations;xn-1,yn-1,zn-1andxn,yn,znare the projectile bodies position locations in the end and the previous simulation time. 3.1 Solver program compared It assumes that the target motion is the uniform linear motion and in the same direction as the bombs’. Two groups of initial condition are chosen to calculate. The conditions are shown in Tab.1. Tab.1 Parameters of simulation Traditional curve fitting method, model calculating method and local precision search method are used in simulation. The results are shown in Tab.2 and Tab.3. Tab.2 Results of condition Ⅰ Tab.3 Results of condition Ⅱ Calculation accuracy of the curve fitting method can meet requirements to the operation mission of horizontal bombing and static target, and the solving time is short. But to the pitch up or dive bomb, off-axis emission and target motion, it has relatively large errors. Due to the storage of airborne computer, the curve fitting method has some certain limitations. Because of long solving time, model calculation also doesn’t meet requirements well. To different solving precisions and times of the operation missions, local accurate searching method can provide a advantageous launch window for carrier aircraft and meet the operational mission’s needs. 3.2 Simulation of allowable attack area Defining the launching ability of reference off-axis as 15°, different solving methods are used to the attack area calculation for stationary and moving targets. The simulation results are shown in Fig.4 and Fig.5. Fig.4 Attack area of static target Fig.5 Attack area of kinetic target The calculation of the whole attack area for the reference off-axis ability is using the local accurate search, curve-fitting and model solving method. The local accurate search and curve-fitting method have more accurate solutions when the target is static. Compared to 106 s of the model solver, 13 s of the local search algorithm as the computation time is significantly reduced, so it is easier for engineering applications. Local accurate search has a more accurate solution when the target is moving. At the far boundary, curve-fitting method doesn’t guarantee sufficient accuracy. So the time of local accurate search, model algorithm and traditional curve-fitting method are 8 s, 95 s and 5 s. Therefore, the local accurate search algorithm can meet the needs of accurate and time. 3.3 Adaptive simulation For complexity of the modern battlefield environments and the variety of combat missions, a carrier aircraft should attack in different operational modes. It puts forward a higher requirement for the calculation algorithm of allowable attack area. The attacking mode in a vertical plane can be divided into dive bombing, level bombing and loft bombing. In different attacking methods, the local accurate searching algorithms are used for the attack area as shown in Fig.6. Fig.6 Attack area for different bombing methods From Fig.6, the local accurate searching algorithm can be used by different carrier aircraft attack methods. No singular values and discontinuous phenomenon are appeared. So this algorithm is more flexible and has a stronger environment suitability for battles. The calculation of attack area is the core requirement of air-surface guided bomb in different launching conditions. The traditional curve-fitting and model calculation method have some limitations to uncertainties of the launch conditions, which include unpredictable target motion and fast computing requirement. This paper put forward the local accurate searching method to make up the deficiency. The method has a certain effect on improving the performance of the fire control system to air-to-surface guided bombs. [1] Liu Daijun, Gao Xiaoguang, Li Yanjun, et al. A fast simulation algorithm for calculating the allowable attack area for air to air missiles[J]. Journal of Northwestern Polytechnical University, 1999, 17(4): 530-533. (in Chinese) [2] Du Changping, Zhou Deyun, Jiang Aiwei. A better method for computing air-to-air missile trajectory[J]. Journal of Northwestern Polytechnical University, 2006, 24(6): 682-685. (in Chinese) [3] Zhang Youji. Tactical missile flight dynamics design[M]. Beijing: Astronautic Press, 1998:58-72. (in Chinese) [4] Qian Xingfang, Lin Ruixiong, Zhao Yanan. Missile flight dynamics[M]. Beijing: Beijing Institute of Technology Press, 2003: 86-111. (in Chinese) [5] Joseph J Siegel Gyor. System preliminary design[M]. Shi Chaoli, transl. Beijing: National Defence Industrial Press, 1965: 157-165. (in Chinese) [6] Garnell P. Guided weapon control systems[M].London: Royal Military College of Science Press, 2004:161-172. [7] Xie Kexin, Han Lixing. Optimization methods [M]. Tianjin: Tianjin University Press,2002:60-65. (in Chinese) [8] Zhang Ping, Fang Wangyang, et al. A new method of real-time calculation for attack area of air-to-air missile[J]. Journal of Ballistics, 2010, 22(4):11-14. (in Chinese) (Edited by Wang Yuxia) 10.15918/j.jbit1004- 0579.201524.0204 TJ 765.3 Document code: A Article ID: 1004- 0579(2015)02- 0164- 05 Received 2013- 11- 30 E-mail: liqiang2568837@126.com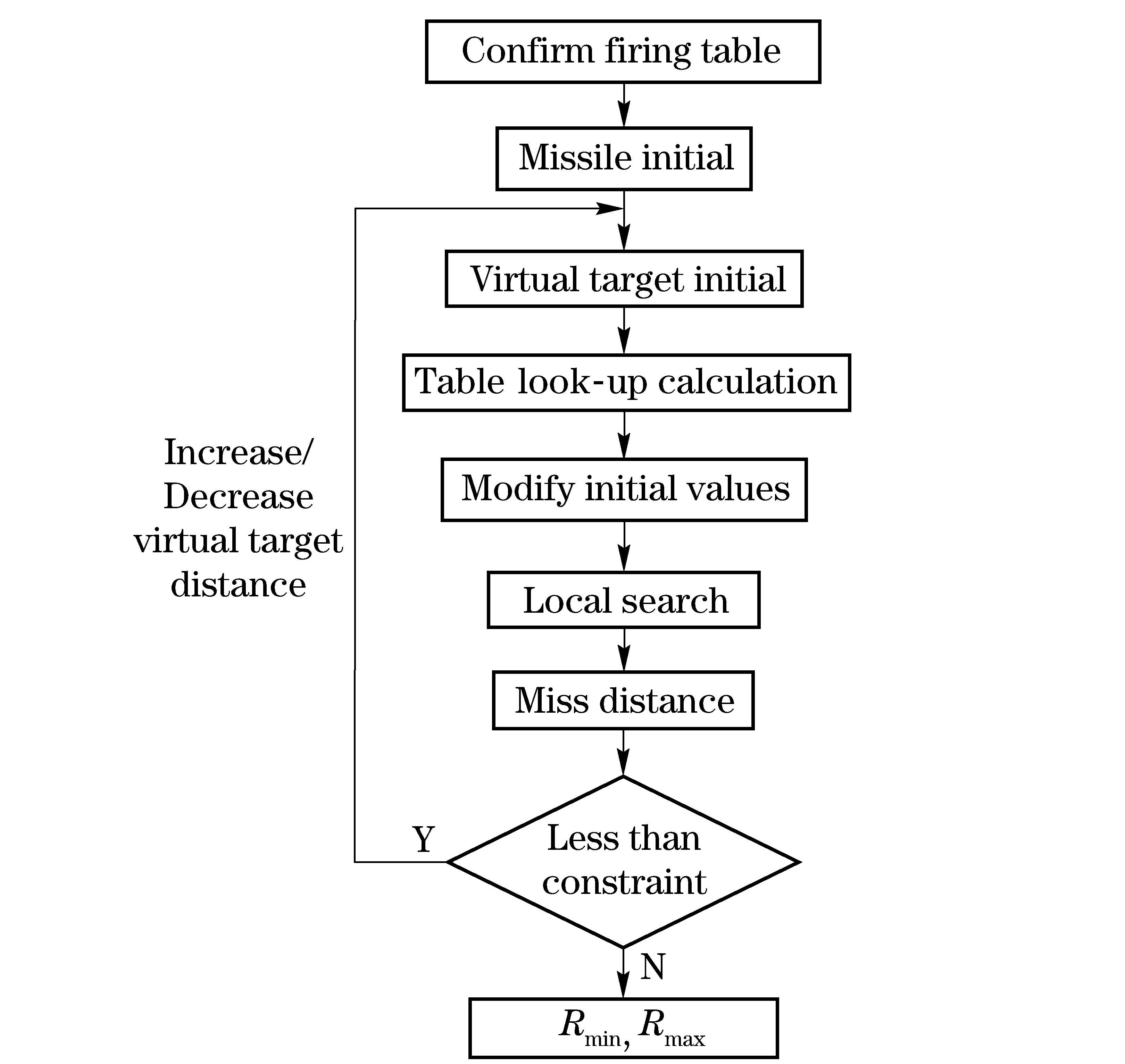
3 Simulation





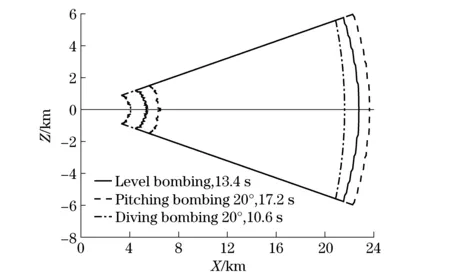
4 Conclusion
 Journal of Beijing Institute of Technology2015年2期
Journal of Beijing Institute of Technology2015年2期
- Journal of Beijing Institute of Technology的其它文章
- Nonlinear symbolic LFT model for UAV
- Novel scheme of high precision inertial measurement for high-speed rotating carriers
- Study on influencing factors of adapters separating with the underwater missile
- Design and analysis of mechanical self-destruction and self-neutralization mechanism for submunition fuze
- Resilience approach for heterogeneous distributed networked unmanned weapon systems
- Modeling and simulation of the static characteristics of diaphragm spring clutches
