Resilience approach for heterogeneous distributed networked unmanned weapon systems

JIN Yi-ning(晋一宁), WU Yan-xuan(吴炎烜), FAN Ning-jun(范宁军)

(School of of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)



Resilience approach for heterogeneous distributed networked unmanned weapon systems

JIN Yi-ning(晋一宁), WU Yan-xuan(吴炎烜), FAN Ning-jun(范宁军)

(School of of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)

Disconnection in the distributed heterogeneous networked unmanned weapon systems is caused by multiple weapon units’ failure. The technical routes were analyzed to achieve resilience in the disconnection situation. A heterogeneous distributed network model of networked unmanned weapon systems was established. And an approach of adding relay weapon units was proposed to achieve fault tolerance after weapon units’ failure due to attack or energy exhaustion. An improved genetic algorithm was proposed to determine and optimize the position of the relay weapon units. Simulation results in the MATLAB show that the improved resilience-based genetic algorithm can restore the network connection maximally when the number of relay units is limited, the network can keep on working after failure, and the implementation cost is controlled in a reasonable range.

distributed heterogeneous network; unmanned weapon system; genetic algorithm； resilience

With the development of communication, computer and network technologies, modern warfare gradually developed from a single-platform combat to a multi-platform network combat[1]. And a network-based combat is becoming an important tendency in the information warfare. Networked unmanned weapon system (NUWS) is a type of intelligent combat system illustrated in Fig.1. It uses the network connection to obtain multi-channel information and processing abilities (even the energy) from different weapon units to complete combat missions, such as battlefield reconnaissance, communication relay, targets attack, and damage assessment. NUWS usually executes missions by its large number of micro and small unmanned weapons units based on the network. After the failures of plenty of weapon units due to attack or energy exhaustion, the network is tore apart. In order to complete the combat tasks, how to restore the connectivity of the network in a certain degree becomes very important. And this is the resilienceproblem we focused on in this paper.

Fig.1 Illustration of NUWS

Currently, there is no public information about the NUWS resilience study, and the related studies are mainly concentrated in the wireless sensor networks (WSN) area. We classify the methods to achieve resilience in WSN into passive methods and active methods. The passive methods are redundancy methods[2-4]. And the active methods are relocating the existing nodes in the network[5-7]or adding extra relay nodes to form multi-hop network connectivity[8-11]. The redundancy methods realize fault-tolerance at the expense of high cost and energy consumption, while the weapon units in NUWS are much more expensive than the sensor nodes in WSN. Thus, it is impossible to deploy weapon units redundantly. Relocating methods are more suitable for small nodes failure scale as only local adjustment is needed. However, when large scale of weapon units are damaged in the battlefield, these methods require a global adjustment of the weapon units, which is inefficient and costly. Above all, the most efficient and low-cost resilience approach for NUWS is to add multiple extra weapon units to restore the network connectivity.

The methods of adding relay nodes are mainly geometric methods, such as the MST-based (minimum spanning tree-based) algorithm[8-10]and CIDT (connectivity improvement using delaunay triangulation) algorithm[11]etc. They mainly focus on finding the least number of relay nodes needed to restore 100% connectivity in homogeneous WSN. However, in the application of NUWS, using a given limited number of relay weapon units to achieve a maximum level of connectivity is much more close to the real situation. Moreover, the geometric methods are not suitable for heterogeneous NUWS. The NUWS is a highly heterogeneous distributed system, which consists of different weapon units that use different communication devices and different communication radius. Therefore, the above methods are not suitable for solving the NUWS resilience problem. In this paper, genetic algorithm is going to be used to calculate and optimize the positions of the relay weapon units, with the purpose of restoring the connectivity of NUWS maximumly by a given limited number of relay weapon units and controlling the cost of implementation.

1 Problem description and system modeling

1.1 Problem description

NUWS is a mobile autonomous combat network without infrastructure support, and the nodes in the network are micro and small unmanned weapon units, which can be employed in the water, on the land or in the sky. Compared with a centralized network, NUWS is a kind of distributed network, in which each weapon unit can only communicate directly with its adjacent units. This provides stronger survivability and invulnerability in harsh battlefield environments. However, due to the volume restriction, weapon units cannot provide enough energy for long-time work, and failures happen after running out of energy. Besides, weapon units may also fail as the results of enemy attack or harsh environments. In this case, the network connectivity has been greatly damaged, which may decrease the capability of NUWS, or even fail to complete the mission.

Therefore the problem needs to be solved is described as follows. For a given area, after the failures of quite a few weapon units, the heterogeneous distributed NUWS becomes disconnected, the target is to calculate and optimize the positions for a given limited number of relay weapon units to restore the connectivity of NUWS maximally and take the implementation cost into consideration. The problem here is a non-deterministic polynomial complete (NPC) problem.

1.2 System modeling

In this paper, it is assumed that each weapon unit in NUWS is distributed randomly within a two-dimensional combat zone, and the damage probability of each unit obeys an exponential distribution and is independent from each other. NUWS is a highly heterogeneous network, and we are mainly focus on the communication heterogeneity in this paper. Each weapon unit has different communication radius. The remaining weapon units in NUWS after failure are called target units and are represented by the set UV={UV1,UV2,…,UVn}; the relay weapon units added into the damaged NUWS are represented by the set UR={UR1,UR2,…,URm}. Assuming that the communication radius of target units areRUVmin≤r(UVi)≤RUVmax, and all relay units have the same communication radiusr(URi)=RUR. Unidirectional communication link is proven to be costly[12], so bidirectional communication path is considered in this paper, along which communications existing in both directions. Thus, when and only when the Euclidean distance between two unitsi,j(i,j∈UV∪UR) is smaller than their communication radius, that isdij≤min (ri,rj), communication is established between them. NUWS is modeled as a undirected graphG=(UV∪UR,E), whereEis the set of all undirected communication links connecting two weapon units inG, the schematic diagram is shown in Fig.2. If and only ifdij≤min (ri,rj), the communication link is established andeij=eji=1.

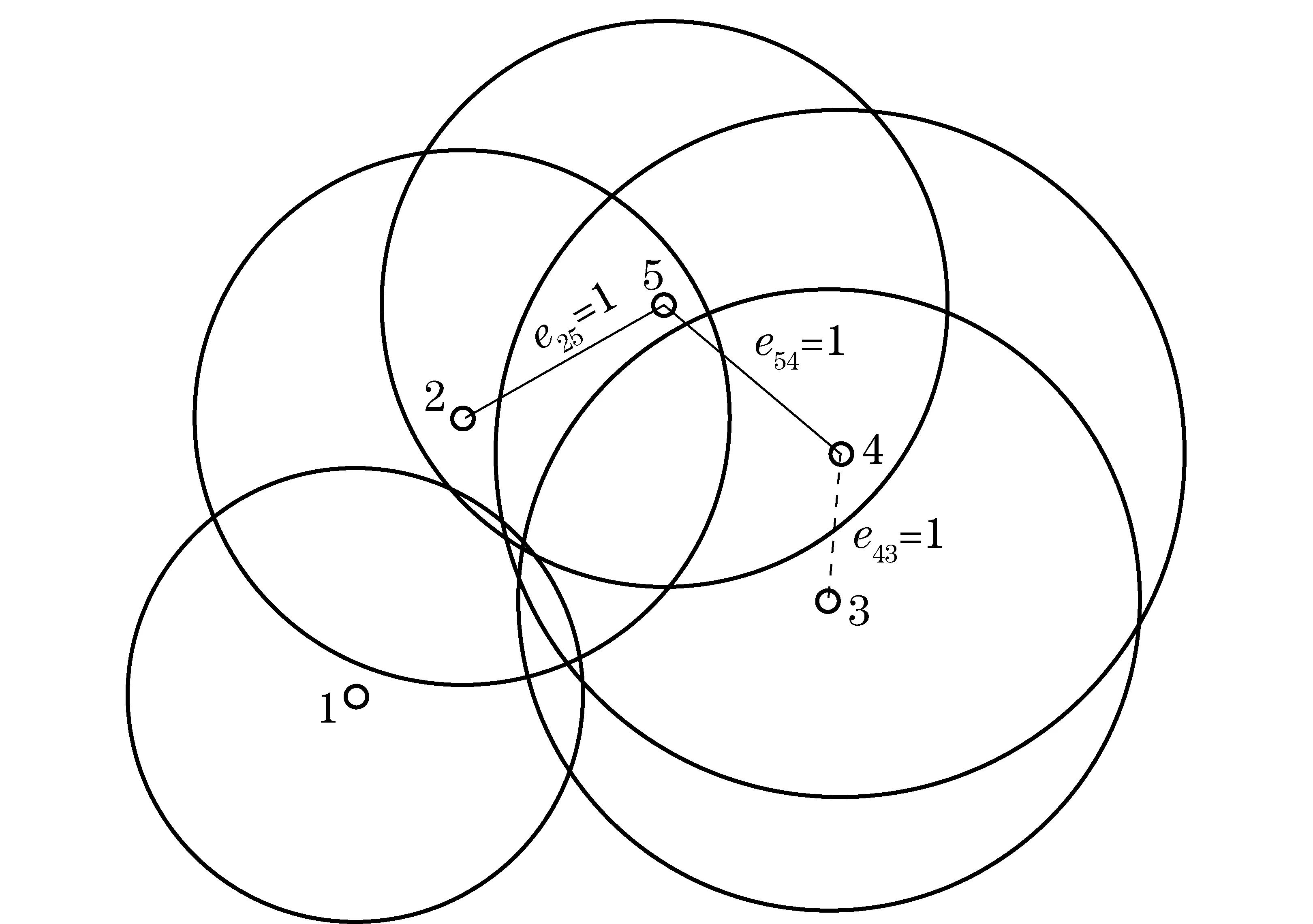
Fig.2 An example of the system model of NUWS

2 Improved genetic algorithm

As the problem here is a NPC problem, the computation increases exponentially with the growing number of weapon units in the NUWS, so it is difficult for numerical algorithms to find an optimal solution for this problem within a limited time. Therefore, the genetic algorithm (GA), a type of intelligent heuristic algorithm, is used here. The GA is based on the biological theory of natural selection and genetic mechanism. It has been proven to be a useful directed random search method for finding the global optima in complex problems with multi-dimensional, non-linear, discontinuous, and non-convex solution spaces. Furthermore, the search strategies and optimization calculations of GA do not depend on the gradient information. Besides, because of its inherent parallelism, GA can effectively handle large scale optimization problems.

In the standard GA, the roulette selection strategy, fixed crossover probability and fixed mutation probability are often used. But the roulette selection strategy will easily cause premature convergences. The small mutation and crossover probabilities will cause a slow and premature convergence, while large probabilities will makethe algorithm fail to converge. Therefore, the GA is improved here to prevent premature convergences[13-14]by combining the elite individual reservation strategy and the roulette selection strategy, and using adaptive crossover and mutation probability. The improved GA is illustrated as follows.

① Encoding and initializing the population. Each chromosome in the population represents a potential location solution of m relay units. Every location is described by the values inxandycoordinates, which are encoded bylbits respectively. It is assumed that the combat zone is ad×dsquare area, the precision of encoding is

(1)

Thesizeofeverychromosomeism×2×lbits. Here,mis the number of relay units added into the NUWS. And the size of population is 60 here, which means it consists of 60 chromosomes. The initial set of population is generated randomly.

② Evaluation. The fitness function evaluates the performance of every chromosome. The aims of this algorithm are to realize resilience by recovering the NUWS’s connections and to control the implementation costs in a reasonable range. This is a multi-objective optimization problem, and the fitness function is designed to have two parts.

The first part describes the performance of restoration, which is to connect the target units as much as possible by using a given limited number of the relay units. This can be described as

(2)

whereN′ is the number of target units in the largest connected component of network,Nis the number of target units in NUWS. The relay units are not included inN′ andN.

The second part is the cost control problem, using the connection degree of relay units to evaluate. For instance, a relay unit is connected withKunits (including relay units and target units), so its connection degree isK. For the convenience of calculation, the connection degree calculation of each relay unit is transformed into the number calculation of edges. Thus, to minimize the cost is considered equal to minimize the increased number of edges. And

ΔE=Eaf-Ebe

(3)

whereΔEisthenumberofincrementalcommunicationlinksafterdeployingtherelayunitsintheNUWS, EafandEberepresentthenumberofcommunicationlinksafterandbeforedeployingtherelayunitsrespectively,andEmaxisthenumberofallthepossiblelinksthatwillmakesthegraphastronglyconnectedgraph.

So,thefitnessfunctionis

(4)

Hereωistheweight,andω=0.6.

Throughthedesignedfitnessfunction,thecommunicationheterogeneousofNUWSissolved.

③Evolutionprocedure.Thepopulationevolvestowardbettersolutionsbyadoptinggeneticoperationsofselection,crossoverandmutationtogeneratethenewpopulation,andthenevaluateituntilmeetingthestoppingcriterion.

Theeliteindividualreservationstrategyarecombinedwiththerouletteselectionstrategyhere.Thespecificprocedureisdescribedasfollows.Theparents,selectedbyarouletteselectionstrategyfromthelastgeneration,areintersectedandmutatedtogenerateoffspring.Andthenfindthebestandworstindividualwiththehighestandlowestscoreoffitnessevaluation.Ifthebestindividualintheoffspringisbetterthanthehistoricalbestindividual,thenewlybestoneisrecordedasthehistoricalbestone;otherwisethehistoricalbestoneiskept.Thereafter,thehistoricalbestindividualisusedtoreplacetheworstindividualintheoffspringtoformanewpopulation.Thus,thebestchromosomeispassedthroughthenewgeneration.

TheadaptivecrossoverprobabilityPcandmutationprobabilityPmareappliedhere,whichare

(5)

(6)

wherefis the larger fitness value of the two individuals going to be crossed,f′ is the fitness value of the individual going to be mutated,favgis the average fitness value of every generation, andfmaxis the fitness value of the largest one in this generation.

In this way, the excellent genes have higher possibilities to be passed to the next generation. And the individuals with below-average fitness have larger crossover and mutation probabilities to increase the possibilities of elimination. Moreover, the outstanding individuals do not take dominate positions in the early stage of evolution, preventing from converging into local optima.

④ Stopping criterion. If the evolutionary generations reach to 500, the algorithm stops and outputs the individual with best fitness and its corresponding positions of the relay units as the optimal solution. Otherwise, the next step is to continue evolution.

3 Simulation and results analysis

Simulations are carried out with the proposed method and improved GA algorithm in MATLAB. The simulation parameters are explained in Tab.1. The restoration performance of the algorithm is evaluated by the connection rate using Eq. (2), and the cost of the implementation is evaluated by the connection degree of relay units.

Tab.1 Parameters in simulation

The NUWS works within a 200 m×200 m square. After failures of plenty weapon units, the NUWS becomes disconnected and divides into several partitions. There arenweapon units left. Considering of their communication heterogeneous, their communication radiuses are random distributed from 10 m to 70 m obeying a uniform distribution. Andmrelay units, whose communication radiuses arer(URi)=30 m, are added into the NUWS to maximally recover the connectivity. Thexandycoordinates of relay units are encoded with an 8 bit binary string respectively. So the accuracy of position encoding is 0.78 m according to Eq.(1), which is much less than the minimum communication radiusRUVmin=10 m in the NUWS, so this encoding length is appropriate. The size of population for the GA is 60, and the generation of evolutionary is 500 here.

By changing the size of the network and the number of relay units, two sets of simulations in MATLAB are carried out to verify the resilience effectiveness of proposed improved GA. And the results are shown in Fig.3 and Fig.4, where the hollow circles represent the target units after damage and the asterisks indicate the added relay weapon units.

The first group of simulation is 30 target units in the NUWS with different ratios of relay units, and the results are shown in Fig.3. There are 30 target units with different communication ranges randomly distributed in the square obeying uniform distribution and the connection rate is βb=0.500 0,whichisdescribedinFig.3a.Whenη=0.1 (m=3)relayunitsareaddedthatisshowninFig.3b,theNUWS’sconnectionratecanberecoveredtoβa=0.600 0.Whenη=0.2 (m=6)relayunitsareaddedthatisshowninFig.3c,theconnectionratecanberecoveredtoβa=0.866 7.AndinFig.3d,whenη=0.3(m=9)relayunitsareadded,theconnectionratecanberestoredtoβa=0.966 7.

Fig.3 Connectivity before and after deployment of relay units with difference pairs of parameters(n=30)

ItisrevealedfromFig.3,improvedGAcansignificantlyrepairthedamagedNUWS’sconnectivitybydeterminingandoptimizingthelocationsoflimitednumberofrelayunits.

Thesecondgroupofsimulationis40targetunitsintheNUWSwithdifferentratiosofrelayunits,andtheresultsareshowninFig.4.

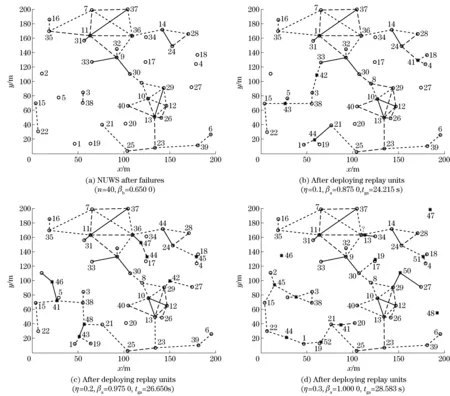
Fig.4 Connectivity before and after deployment of relay units with difference pairs of parameters(n=40)

ItisshownthatthecalculationtimeofGAgrowsfrom17.091sto28.583s.AlthoughthetimeriseswiththeincreasingnumberoftargetunitsandrelayunitsintheNUWS,itisstillacceptablewhenunder60s.

Comparedthetwogroupsofsimulationabove,itisseenthatwhenn=30,themorerelayunitsareadded,themuchmorehighertheconnectionratesare.Butwhenn=40,theconnectionratesarenotsignificantlyraisedwhentheratioofrelayunitsisincreasedfromη=0.2toη=0.3.Toanalyzethisphenomenon,differentparametersofsimulationarecarriedoutfor100times,accordingtothestatisticaldata,theNUWS’saverageconnectionratesbeforeandafterdeploymentofrelayunitsareshowninFig.5.

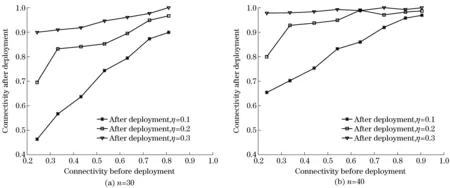
Fig.5 Average connectivity over 100 times with difference pairs of parameters

ThehorizontalaxisinFig.5showstheaverageconnectionratebeforerestoration.Becauseoftherandomlydistributionofthetargetunits’positionsandtheircommunicationradius,theconnectionratesβbaredifferentevenwhenthenumberoftargetunitsintheNUWSisthesame.Whenn=30,theconnectionrateβbisdistributedintherange(0.2, 0.9),andwhenn=40, βbisdistributedintherange(0.2, 1.0).Theverticalaxisshowstheaverageconnectionrateβaafterrepairing,,andlineswithdifferentsymbolsindicatedifferentratiosofrelayunitsaddedintotheNUWS.ItisillustratedintheFig.5thattheapproachcansignificantlyreconnectthedamagedNUWSandincreasetheconnectionrate.Anditshowsthattheperformanceofconnectionrecoveryisrelatedwiththenumberofrelayunitsandthetargetunits,andtheconnectionrateβb.

WhentheNUWS’sconnectionrateafterrestorationisβa≥0.900 0,theresilienceisconsideredtobeachievedandthefunctionoftheNUWSwillnotbeaffected.Thus,whentheratioofrelayunitsaddedintotheNUWSisη=0.3,theresilienceisobtained.

Meanwhile,thestatisticsdatashowthattheconnectivitydegreeofrelayunitsafterdeploymentisnomorethan4,i.e. Kmax≤4.AndmostoftheconnectivitydegreesareK=2andK=3.Therefore,theimprovedGAproposedherenotonlyrepairedtheconnectionofNUWStosomeextent,butalsoithasprovidedacertainredundancyandenhancedresilience.Moreovertheconnectiondegreesarenotmorethan4,sotheimplementationcostislow.

4 Conclusion

TheresilienceproblemofdistributedheterogeneousNUWSisstudiedinthispaper.Apracticalapproach,addingrelayweaponunitsintotheNUWS,isproposedheretorestoretheconnectivitybetweentheremainingtargetunitsofNUWSafterthefailuresofplentyweaponunits.Thecommunicationrangedifferenceisconsideredasthemainheterogeneouscharacteristicsoftheweaponunitsinthispaper.TheGAisimprovedherebycombiningtheeliteindividualreservationstrategyandtherouletteselectionstrategy,andusingtheadaptivecrossoverandmutationprobabilitytopreventprematureconvergences.ThecodingandfitnessfunctionaredesignedforthismodifiedGA,whichisusedtodetermineandoptimizethepositionsofrelayunits.SimulationresultsinMatlabshowthattheproposedmethodhasagoodperformance,whichiscapableofmaximizingtheconnectivityoftheNUWSwithagivenlimitednumberofrelayunits.MeanwhiletheconnectiondegreeofrelayunitisK≤4fromthestatisticsdata,sotheimplementationcostislow.

[1] Fu Xiaowei, Li Jinliang, Gao Xiaoguang. Modeling and analyzing of air-defense threat netting[J].Acta Armamentarii, 2013, 34(7): 904-909. (in Chinese)

[2] Guo Wenzhong, Xiong Naixue, Athanasios V Vasilakos. Distributed k-connected fault-tolerant topology control algorithms with PSO in future autonomic sensor systems[J]. International Journal of Sensor Networks, 2012, 12(1): 53-62.

[3] Taul Bari, Arunita Jaekel, Jin Jiang. Design of fault tolerant wireless sensor networks satisfying survivability and lifetime requirements[J].Computer Communications, 2012, 35(3): 320-333.

[4] Randles Martin, Lamb David, Odat E. Distributed redundancy and robustness in complex systems[J].Journal of Computer and System Sciences, 2011, 77(2): 293-304.

[5] Ameer A Abbasi, Mohamed Younis, Kemal Akkaya. Movement-assisted connectivity restoration in wireless sensor and actor networks[J].IEEE Transactions on Parallel and Distributed Systems, 2009, 20(9): 1366-1379.

[6] Kemal Akkaya, Fatih Senel, Aravind Thimmapuram. Distributed recovery from network partitioning in movable sensor/actor networks via controlled mobility[J].IEEE Transactions on Computers, 2010, 59(2): 258-271.

[7] Cheng Xiuzhen, Du Dingzhu, Wang Lusheng. Relay sensor placement in wireless sensor networks[J].Wireless Networks, 2008, 14(3): 347-355.

[8] Errol L Lloyd,Xue Guoliang. Relay node placement in wireless sensor networks[J].IEEE Transactions on Computers, 2007, 56(1): 134-138.

[9] Lee Sookyoung, Mohamed Younis. Optimized relay node placement for connecting disjoint wireless sensor networks[J].Computer Networks, 2012, 56(12): 2788-2804.

[10] Lee Sookyoung, Lee Meejeong. QRMSC: efficient QoS-aware relay node placement in wireless sensor networks using minimum Steiner tree on the convex hull[C]∥International Conference on Information Networking (ICOIN), 2013: 36-41.

[11] Li Ning, Hou Jennifer C. Improving connectivity of wireless ad hoc networks[C]∥Mobile and Ubiquitous Systems: Networking and Services, 2005: 314-324.

[12] Ravi Prakash. Unidirectional links prove costly in wireless ad hoc networks[C]∥DIALM’99 Proceedings of the 3rd International Workshop on Discrete Algorithms and Methods for Mobile Computing and Communications, 1999: 15-22.

[13] Lei Yingjie, Zhang Shanwen, Li Xuwu. MATLAB genetic algorithm toolbox and its application[M].Xi’an: Xi’an University of Electronic Science and Technology Press, 2005: 11-31. (in Chinese)

[14] Wang Xiaoping, Cao Liming. Genetic algorithms—theory, application and software implementation[M].Xi’an: Xi’an Jiaotong University Press, 2002: 73-74. (in Chinese)

(Edited by Wang Yuxia)

10.15918/j.jbit1004- 0579.201524.0207

E 837; TP 393 Document code: A Article ID: 1004- 0579(2015)02- 0180- 08

Received 2013- 11- 05

Supported by the Aviation Science Foundation of China(2013ZC72006)

E-mail: alexwyx@bit.edu.cn