Design and analysis of mechanical self-destruction and self-neutralization mechanism for submunition fuze

XU Sheng-gang(许胜刚), WU Yan-xuan(吴炎烜), FAN Ning-jun(范宁军)

(School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)



Design and analysis of mechanical self-destruction and self-neutralization mechanism for submunition fuze

XU Sheng-gang(许胜刚), WU Yan-xuan(吴炎烜), FAN Ning-jun(范宁军)

(School of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100081, China)

In order to decrease the unexploded submunition rate and reduce the harmfulness of unexploded submunition, a mechanical self-destruction and self-neutralization mechanism for submunition fuze is proposed in this paper. The definitions of the self-destruction and self-neutralization for submunition fuze are elaborated, and the action principle of the mechanical self-destruction and self-neutralization mechanism is also analyzed. A dynamic model is established with an analysis on centrifugal plate parts, and the feasibility of mechanism motion is also discussed. A virtual prototype of mechanism is formed, and the motion process simulation of the mechanism is performed through a dynamic analysis software ADAMS. The centrifugal experiment results validate that the mechanical self-destruction and self-neutralization mechanism can act reliably.

submunition; unexploded submunition rate; self-destruction; self-neutralization

Cluster munition has many characteristics including intensive instantaneous fire, large covering area and huge damage efficiency, etc. It not only ensures the destruction to effective strength in the target region such as cluster point of armored target and airfield runway, but also makes up the deficiency of the low accuracy of uncontrolled ammunition and the larger absolute dispersion of surface-to-surface missile, and complies with the feature of depth attack in modern warfare[1-2]. At the same time, more and more attention is paid to the unexploded problem of submunition by all parties[3]. The main reason for the international attention caused by the cluster munition problem includes two aspects: ① the cluster munitions cannot identify the military and non-military targets accurately, and cannot have the selective attack to the military target; ② a large number of the cluster munitions were used, whose fuzes have a low sparking rate, so there were a lot of unexploded submunitions (10%-30%), which caused long-term harm to the civilians and environment[4]. In order to decrease the unexploded submunition rate and reduce the harmfulness of unexploded submunition, both at home and abroad the improvement measures aiming at submunition fuze mainly consists of improving the reliability of the main firing action of the fuze and adding self-destruction, self-neutralization and self-deactivation (“three-self” for short) function. Among them, improving the reliability of the main firing action and adding the function of self-destruction can decrease the rate of unexploded submunition; adding the function of self-neutralization and self-deactivation can reduce the harmfulness of unexploded submunition. For the conventional, general, inexpensive and small submunition, the technology of improving the reliability of the main firing action is difficult, and the cost is high. In contrast with the former, adding “three-self” function to submunition has advantages of shorter development period, smaller technical risk and lower cost. This method is adopted generally abroad. All kinds of submunition fuze’s structures meeting the requirements of protocol mentioned above were introduced on American 47th-51st Annual Fuze Conference, which either added powder or electronic self-destruction[5-11]. Microminiature power technology suitable for submunition fuze is immature by far in China, and it is difficult to solve the problem of long-term storage with the gunpowder technology. Therefore improving the traditional mechanical structure of submunition fuze to possess the “three-self” function is one of the development trends. At present in China, the research of the mechanical “three-self” theory for submution fuze has just begun[12-13]. We take a certain submunition fuze in our country as the research object. According to the characteristics of the action process of submuniton and the theory of mechanics, one kind of mechanical self-destruction and self-neutralization mechanism is provided, which equips submunition fuze with the function of self-destruction and self-neutralization.

1 Modeling analysis of the mechanism

1.1 Relevant definitions

Self-destruction device is the automatic deviceinside or attached to the ammunition which makes the ammunition to be destroyed.

Self-neutralization device is the automatic device inside the ammunition which makes the ammunition unable to work[12, 14-15].

Each of the above definitions presents a core concept which has clear connotation and broad denotation. The core concept of the self-destruction device is that the fuze can blow the whole submunition up automatically. The core concept of the self-neutralization is that the fuze loses the ability of detonating the submunition automatically.

1.2 Action principle

After submunition is separated out of mother bombs, it enters into the stable falling stage at a certain speed over a period of time. The rotating speed of submunition decreases rapidly after falling to the ground or hitting the objective. The mechanical self-destruction and self-neutralization mechanism of submunition fuze works by using the characteristics of the environmental forces during the process. The schematic diagram is depicted in Fig.1.

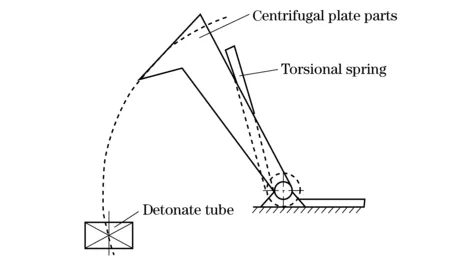
Fig.1 Principle diagram of the mechanical self-destruction and self-neutralization mechanism

① After submunition is separated out of mother bombs, it enters into the falling stage. When the submunition’s rotating speed increases to a certain numerical value, the centrifugal plate parts compress torsional spring to rotate outward under the effect of centrifugal force.

② When the rotating speed of submunition increases to a certain numerical value, the centrifugal plate parts can fly away completely and keep the state all the time before falling to the ground or hitting the object.

③ When submunition falls to the ground or hits the objective, its rotating speed decreases. When the rotating speed decreases to a certain numerical value, the centrifugal plate parts can rotate inward until they stab detonate tube.

1.3 Modeling analysis

Based on the simplification of the centrifugal plate parts, the model is set up shown in Fig.2.

Consider the geometry of Fig.2. Take the symmetry plane of centrifugal plate parts perpendicular to submunition’s rotation axis as the study plane, denoted byOXY.OXYis a rectangular coordinate system, which is a non-inertial reference system attached to submunition and also makes the translation motion and rotation with submunition. The intersection of submunition’s rotation axis andOXYis origin of coordinates, denoted byO,O′ is the intersection of centrifugal action mechanism’s rotation axis andOXY,Xaxis alongs the direction ofOO′.Cdenotes the centroid of centrifugal action component, when the centrifugal plate parts rotate to the limit position, the location of centroid changes toC′,C″ is the location of centroid when the centrifugal plate parts are under assembling condition, B denotes the action point on centrifugal plate parts by torsional spring, initial position of torsional spring under natural state (namely non-pressure) is denoted byO′D. In the whole action process, the centrifugal plate parts are treated as a rigid body, regardless of elastic-plastic deformation.

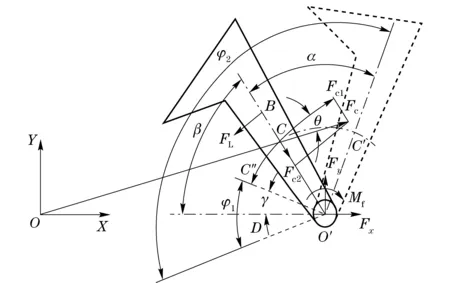
Fig.2 Simplified model of the centrifugal plate parts

The centrifugal force on the centrifugal plate parts is

Fc=mLω2

(1)

wheremis the mass of centrifugal plate parts;Lis the distance between submunition’s rotation centerOand centroidCof centrifugal plate parts.ωis the rotating speed of submunition.

Decomposing centrifugal forceFcinto component forcesFc1andFc2, whereFc1is along the direction ofCO′ andFc2is perpendicular to the direction ofCO′.

Fc1=Fccosθ=mLω2cosθ

(2)

Fc2=Fcsinθ=mLω2sinθ

(3)

whereθis the angle betweenFc1andFc2.

Using the principle of force balance, constraint force oncentrifugal plate parts by their rotation axis can be written as follows

(4)

whereFLis the action force of torsional spring on the centrifugal plate parts.

Three moments are forced on centrifugal plate parts during the motion.

① The centrifugal moment

MC=Fc1r=mLω2rcosθ

(5)

whereris the distance from centrifugal plate parts’ rotation axis to their centroidC.

② The moment generated by torsional spring

(6)

whereM1is the average torque of torsional spring under the assembling condition；M2is the average torque when torsional spring rotates to the limit position；φ1is the average torsional angle of torsional spring under the assembling condition；φ2is the average torsional angle when torsional spring rotates to the limit position;αis the angle betweenO′CandO′C′;r′ is the friction moment on rotation axis of centrifugal plate parts.

③ The friction moment on rotation axis of the centrifugal plate parts

(7)

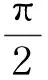
Rotating equation created on rotation axis by centrifugal plate parts is described as

(8)

whereJ0is the moment of inertia of centrifugal plate parts relative to its rotation axis.

Relationship is clearly obtained from Fig.2 as follows

(9)

(10)

Therefore,thedynamicmodelofcentrifugalplatepartscanbesummarizedas

(11)

2 Feasibility analysis of mechanism motion

2.1 Start-up rotating speed

Under assembling condition, the moment on axis of centrifugal plate parts by centrifugal force is

(12)

wheree1is the initial eccentricity from centroid of centrifugal plate parts to rotating axis of submunition;ω1is the angular velocity of submunition.

The pre-twist moment of torsional spring is

ML1=CTα1

(13)

whereCTis the average rigidity value of torsional spring;α1is the pre-twist angle of torsional spring when it is assembled.

The order of magnitude of the friction moment is smaller compared with the centrifugalmoment’s, so it is ignored. When the centrifugal plate parts start, the moment on rotation axis of centrifugal plate parts by centrifugal force is equal to pre-twist moment of torsional spring. That is

MC1=ML1

(14)

Substituting Eqs.(12)(13) into Eq.(14), we have

(15)

Withthedata

179.3 rad/s

The start rotating speed is

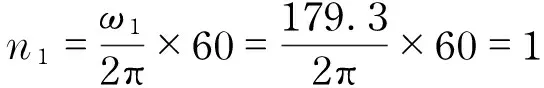
2.2 Rotating speed required for centrifugal plate parts to fly away completely

When the centrifugal plate parts fly away completely, the moment on axis of centrifugal plate parts by centrifugal force is

MC2=me2ω2r

(16)

wheree2is the eccentricity of centrifugal plate parts when they fly away completely;ω2is the angular velocity of submunition.

The moment of torsional spring is

ML2=CT(α1+α2)

(17)

whereα2is the twist angle of centrifugal plate parts.

When the centrifugal plate parts fly away completely, ignoring the friction moment, the moment on rotation axis of centrifugal plate parts by centrifugal force is equal to twist moment of torsional spring. That is

MC2=ML2

(18)

Substituting Eqs.(16)(17) into Eq.(18), we have

(19)

Withthedata

194.9 rad/s

The rotating speed needed for centrifugal plate parts to fly away completely is

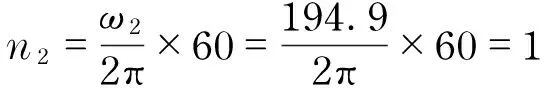
The rotating speed of submunition is 2 700-3 200 r/min when the submunition is in the stable falling stage, which isgreater than 1 862.1 r/min.

Based on the above theoretical analysis, the following conclusions can be made. In the falling process, the centrifugal plate parts are able to start, reach the state of flying away completely and keep the state all the time before falling to the ground or hitting the objective. When submunition falls to the ground or hits the objective, its rotating speed decreases. When the rotating speed decreases to a certain numerical value, the centrifugal plate parts rotate inward under the action of torsional spring, stab the self-destruction or the self-neutralization detonate tube, which implements the self-destruction or self-neutralization of fuze.

3 Simulation analysis

The paper utilizes dynamic simulation software ADAMS to simulate the rotation process of the centrifugal plate parts of the mechanical self-destruction and self-neutralization mechanism. Use the 3D drawing software to establish the virtual prototype, and import the virtual prototype into the ADAMS. Set the properties for each part and the constraints between parts. Set the stable rotating speed of submunition as 2 700 r/min, namely, 16 200°. The simulation curves are shown in Fig.3.

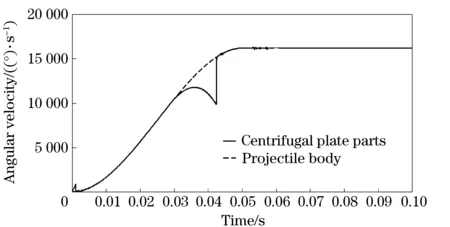
Fig.3 Change curves of angular velocity of the centrifugal plate parts and the projectile body

① The dotted line is the change rule curve of angular velocity of the projectile body. The angular velocity increases at first, then the rotating speed holds steady when the submunition enters the stable falling stage. The simulation accords with the actual process.

② The continuous line is the change rule curve of angular velocity of the centrifugal plate parts. In the initial phase, the centrifugal plate parts rotate together with the projectile body and the angular velocity increases. When the moment on rotation axis of centrifugal plate parts by centrifugal force is greater than the torsional spring torque and friction moment, the centrifugal plate parts start to open. When the centrifugal plate parts reach the limit position (cling to inner wall of fuze cover), the opening process finishes. Then the centrifugal plate parts rotate together with the projectile body again, and rotate at the steady speed eventually. The simulation matches the actual process.

③ When the centrifugal plate parts start up, the rotation speed of the projectile body is 10 636.1(°)/s, namely, 1 772.7 r/min. In the previous analysis, the start-up rotary speed of the centrifugal plate parts is 1 713.1 r/min, and the simulation value is slightly greater than the calculated value because of the friction torque ignored in the process of calculation. The difference value between them is in a reasonable range.

④ Before the projectile body arrives at the steady speed, the centrifugal plate parts can open and fly away completely. For the centrifugal plate parts, the back-stab process is the inverse process of the opening process. So the centrifugal plate parts can be inferred to accomplish back-stab process reliably.

4 Experimental verification

Based on the design and analysis above, the sample machine of the mechanical self-destruction and self-neutralization mechanism is manufactured out. The centrifugal experiment of the sample machine is performed. The sample machines used in the experiment and their internal parts are shown in Fig.4 and Fig.5.

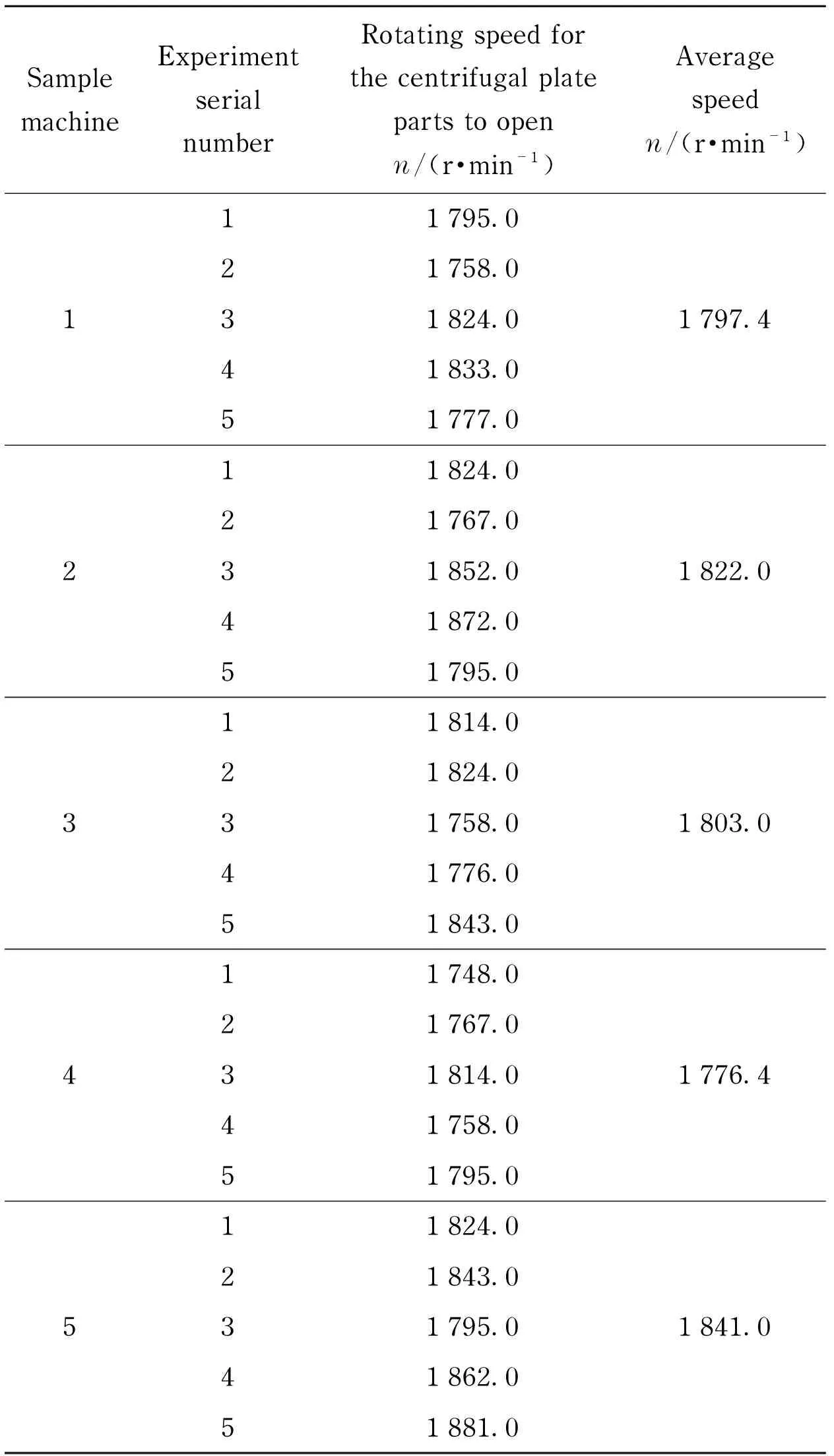
The experimental method can be described as follows: At first the sample machine should be fixed on the centrifugal experiment bench, which is depicted in Fig.6. Then as the rotating speed of the centrifugal machine is slowly increased, record the rotating speed when the centrifugal plate parts fly away. In the experiment five sets of sample machines are used and each one is tested for five times. Tab.1 lists the experiment results.

Fig.4 Sample machines

Fig.5 Internal parts of the sample machine

Fig.6 Centrifugal experiment bench

During the trials, all the centrifugal plate parts of the sample machines can fly away successfully under the action of the centrifugal machine. The fact that the action process of each sample machine meets the design requirements can be found through observing the experimental process. As shown in Tab.1, the five experiment values of each sample machine are close to each other. The average rotating speed of the centrifugal machine for each sample machine when the centrifugal plate parts fly away can be obtained. There are only small differences between the five average speeds.

Tab.1 Centrifugal experiment data

With the simulation analysis, the rotating speed of the projectile body when the centrifugal plate parts fly away is 1 772.7 r/min. From the Tab.1, the average rotating speed of the five sets of sample machines can be calculated to be 1 807.9 r/min. The simulation value is smaller than the experimental value. Limited to some assumptions of simulation analysis, processing precision of sample machine, and test precision of the rotating speed, there inevitably exists certain difference between the simulation result and the experimental result, but it is tolerable.

Combined with theoretical calculation, simulation analysis and experiments of the sample machines, the following facts can be obtained: For mechanical self-destruction and self-neutralization mechanism designed in this paper, the rotating speed required to prompt the centrifugal plate parts to fly away is about 1 800 r/min. It is less than the submunition’s stable rotating speed of 2 700-3 200 r/min. It indicates that the parts can act reliably during the stable falling stage of submunition and the design of the mechanism is reasonable.

5 Conclusions

① In this paper a kind of the mechanical self-destruction and self-neutralization mechanism is proposed, which is applicable to submunition fuze. The relevant definitions are expounded. The dynamic analysis and modeling are also made for the centrifugal plate parts.

② The feasibility of mechanism motion is analyzed. The numerical calculation results show that the centrifugal plate parts can open fully in the falling stage, and when submunition falls to the ground or hits the objective, the centrifugal plate parts can accomplish back-stab process reliably.

③ The dynamics of the mechanism is simulated by ADAMS. The sample machine is manufactured, and the centrifugal experiment is conducted. The simulation and experimental results demonstrate that the mechanical self-destruction and self-neutralization mechanism designed in this paper can act reliably, which meets the design requirements.

[1] Wang Dewu, Cao Yanwei, Dong Jing. Summary of cluster bomb technology development under the background of international armament control [J]. Journal of Detection & Control, 2010(4): 1-6. (in Chinese)

[2] Zhao Yuqing, Wang Xiaobo, Zhang Haijuan. Convention on cluster munition and development trend of submunition fuze [J]. Journal of Detection & Control, 2009, 31: 25-29. (in Chinese)

[3] Zhi Binwei, Ma Baohua. Self-destroying technology of cluster bomb’s submunition fuze [J]. Journal of Detection & Control, 2008, 30(1): 6-10.(in Chinese)

[4] Qin Dongze. “Three-self” design theory and implementation methods of cluster submunition fuze [D]. Beijng: Beijing Institute of Technology, 2013. (in Chinese)

[5] L3 Communications BT Fuze Products. M234/M235/M236 self-destruct fuzes [C]∥47th Annual Fuze Conference, Charleston, USA, 2003.

[6] Srrickland Shala M. Adding an electronic self destruct mode to the destruct mode to the M230 fuze[C]∥47th Annual Fuze Conference, Charleston, USA, 2003.

[7] Harbrecht Rudof. Pyrotechnic bomblet self destruct fuze (SDF) for GMLRS[C]∥48th Annual Fuze Conference, Charlotte, USA, 2004.

[8] Hiebel Mike, Glickman Ilan. Self destruct fuze for M864 projectiles/ MLRS rockets [C] //48th Annual Fuze Conference, Charlotte, USA, 2004.

[9] Yoo Jone. Self-destruct fuze [C]∥51st Annual Fuze Conference, Nashville, USA, 2007.

[10] L3 Communications BT Fuze Products. Low cost p-SDF for ICM rounds [C]∥51st Annual Fuze Conference, Nashville, USA, 2007.

[11] Hiebel Mike. XM242 pyrotechnic self destruct fuze (p-SDF) for 155mm M864 E2 recap [C]∥51st Annual Fuze Conference, Nashville, USA, 2007.

[12] Qin Dongze, Fan Ningjun. Theoretical exposition of fuze harm-reducing system in cluster munitions [J]. Transactions of Beijing Institute of Technology, 2013, 33(3): 225-228. (in Chinese)

[13] Qin Dongze, Fan Ningjun. Weight distribution of sub-munition fuze design[J]. Journal of Beijing Institute of Technology, 2013, 22(2): 153-157.

[14] GGE. Draft protocol on cluster munitions [R]. Genevese: CCW, 2010.

[15] GGE. Draft protocol on cluster munitions [R]. Genevese: CCW, 2010.

(Edited by Wang Yuxia)

10.15918/j.jbit1004- 0579.201524.0206

TJ 430 Document code: A Article ID: 1004- 0579(2015)02- 0173- 07

Received 2013- 12- 20

Supported by the Ministerial Level Advanced Research Foundation(51305040401)

E-mail: alexwyx@bit.edu.cn