Un-powered gliding aircraft’s ballistic missile optimal design

HE Chang-jian(何昌见), MENG Xiu-yun(孟秀云)

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.The First Research Institute of Ministry of Public Security of PRC, Beijing 100048, China)



Un-powered gliding aircraft’s ballistic missile optimal design

HE Chang-jian(何昌见), MENG Xiu-yun(孟秀云)1

(1.School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;2.The First Research Institute of Ministry of Public Security of PRC, Beijing 100048, China)

In this dissertation, un-powered gliding aircraft’s optimal extended rangeproblem is discussed. The aircraft movement model was built. According to the degree of coupling, the model can be classified into a simple model or a complicated model. Using an optimal control method, two different movement models gave out the aircraft’s attitude angle optimal flight path. Complicated model’s optimal solution can be found by the genetic algorithm. This method can transfer the analytic solution of complicated model to a numerical value solution. Comparing the simulation results of different methods, it showed that the genetic algorithm combined with the complicated model’s numerical value solution had the best performance in control strategy. This method solved the problem in which the highly coupling complicated model’s analytic solution was hard to obtain. It verified that the genetic algorithm has validity in the field of extended range solution searching.

optimal enhance distance problem; optimal control; genetic algorithm; highly coupling complicated model

Un-powered gliding aircraft is a kind of aircraft having aerofoil or empennage, which usually has the ability of gliding in the air. In order to extend the battle field range an optimal control modeling method based on the target function were brought forward[1]. If a guiding control system can control the aircraft by a special gliding angle, it can increase un-powered gliding aircraft flight distance and make the un-powered gliding aircraft fly to the target by a special ballistic obliquity and ending velocity. Optimal ballistic trajectory can be investigated by a special data base[2]. An optimal model according to different time,field of fire,hitting precision can be built[3]. Modeling method can be used in the problem of gliding aircraft’s ballistic missile[4]. The target function is based on gliding aircraft’s distance increasing resulting into building two different models[5-6]. The genetic algorithm were used to calculate optimal increase flight range[7-10]. According to the documents mentioned above, aircraft’s vertical movement model can be divided into two different models: a simple model and a complicated model. They were different in coupling degree. The complicated model has more information compared with the simple model. So it performs better in the optimal enhance distance strategy. It was hard to calculate the analytic solution for the complicated model. The genetic algorithm was used in the searching strategy of the numerical value solution. The simulations of different optimal control methods can be compared. The results showed the best optimal control method. This paper having an important meaning in increasing un-powered gliding aircraft’s field of fire and gliding ability.

1 Ballistic trajectory optimize based on simplify model

Because optimal control analytic solution is complicated to calculate, we simplify the lengthways ballistic missile model and aircraft lengthways ballistic missile model to build estate equation groups. This group include distance、altitude and velocity’s estate variables, equations also include a gesture angle equation, so ballistic trajectory reference frame estate equations group are

(1)

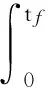
(2)

Outoftheintegralmarkisaterminaltargetfunctionwhichistherequesttotheterminalandinsidetheintegralisthedynamictargetfunction.Thisisfromt0to endpointtfthe whole process require an optimal criterion.

First according to the target function and giving out the Hamilton function:

(3)

Concomitancyfunctionis

(4)

(5)

Terminalconditionis

(6)

(7)

(8)

Concomitancyfunctionλy,λvmustsatisfytheterminalcondition,bycalculatingdifferentialequationsλy,λv’sanalyticsolutioncanbecalculated.Fromtheconcomitancyfunction,theterminalconditioncanget:

λy(t)=0

(9)

λv(t)=sinθ+a1

(10)

Thereina1is an unknown constant.

From sin (θ(tf))+a1=c1(v-v(tf))thata1=c1(v-v(tf))-sin(θ(tf))whichisHamiltonfunctiondifferentialcoefficient， Hminimumvaluefromθcanbeobtained:

(11)

Bybringingλvandλyinto

we get

wherea1is a pending unknown constant. It can be different values ifv(tf) changes in thec1(v-v(tf)). This item can restrict velocity.

2 Ballistic trajectory optimize based on complicated model

Lengthways complicated model include distance, height, velocity and ballistic trajectory estates variable, function also include the gesture angle and others,so complicated model estate functions:

(12)

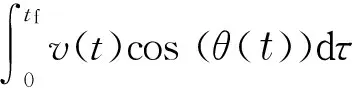
(13)

Thistargetfunctiononlyintheintegralisadynamictargetfunction,thisisfromt0to terminal timetfthe whole process need the optimal criterion and the whole integral represents the maximum horizontal distance.

Hamilton function is

(14)

Concomitancyfunctionis

(15)

(16)

(17)

vsinθ-λyvcosθ

(18)

Terminal condition is

(19)

(20)

(21)

(22)

H’s differential equation about θis

(23)

(24)

Becausetheconcomitancyfunctionishighlycoupling,thesolutionofnumericalcalculationcanbeadopted.Afterusingit,wefoundθvibrate.

Ifwemadeλv=c1v,λy=0,λθ=c2θinheuristics,aneasysolutionisfound.Sothesolutionis

(25)

Therein,c1=-0.02,c2=0.004.

3 Genetic algorithm and simulation contrast

An analytic solution of optimal control in complicated model is hard to get. We consider to combine optimal control with genetic algorithm. Using the genetic algorithm, the result of optimal control can be found. The distance may be increased when using a searched optimal result.

3.1 Searching method in genetic algorithm

3.2Contrastofdifferentsimulationplans

Theconditionsofinitializationareheight10kmandspeed250m/s.Thethreetrajectorysimulationscanbecompared.Theitemswecareaboutaretherestrictionofspeed(Fig.1),theattitudeangle,thedistanceofballistictrajectoryandthedragratio.

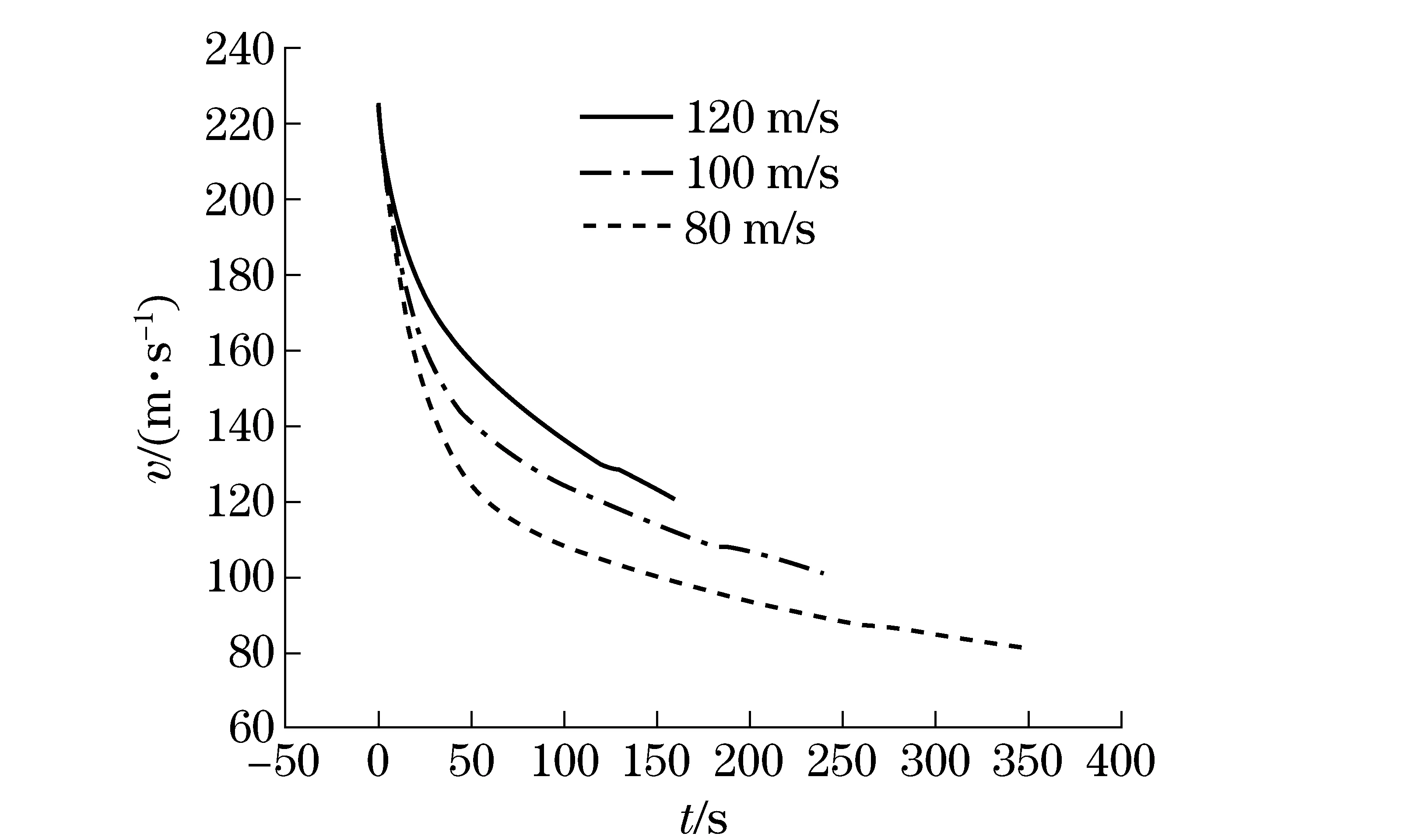
Fig.1 Different speed restrictions of simplify model

Fig.2showsthatgeneticalgorithmmethod’sattitudeangleisthesmallestinthreeplans.Alltheattitudeanglesarestable.Fig.3showsthattheaircraftglidesthelongestdistancewhichis46.7kmbyusingthegeneticalgorithm.Theaircraft’sglidingdistanceis38.5kmbyusingthecomplicatedmodel.Theaircraft’sglidingdistanceis43.5kmbyusingthesimplemodel.Theaircraftglides34-36km,ifitonlyusesguidanceratio.Afterusingplans,thedistancehasincreasedby10km.Fig.4showsthattheplanusinggeneticalgorithmhasthehighestdragratiowhichisupto7.0.Simplemodelplan’seffectwasbetterthancomplicatemodelplan.Geneticalgorithmplanisthebest.

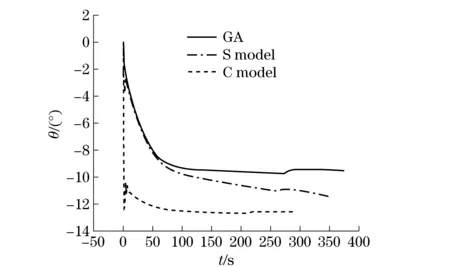
Fig.2 Attitude angle contrast of genetic algorithm, complicated model, simplify model

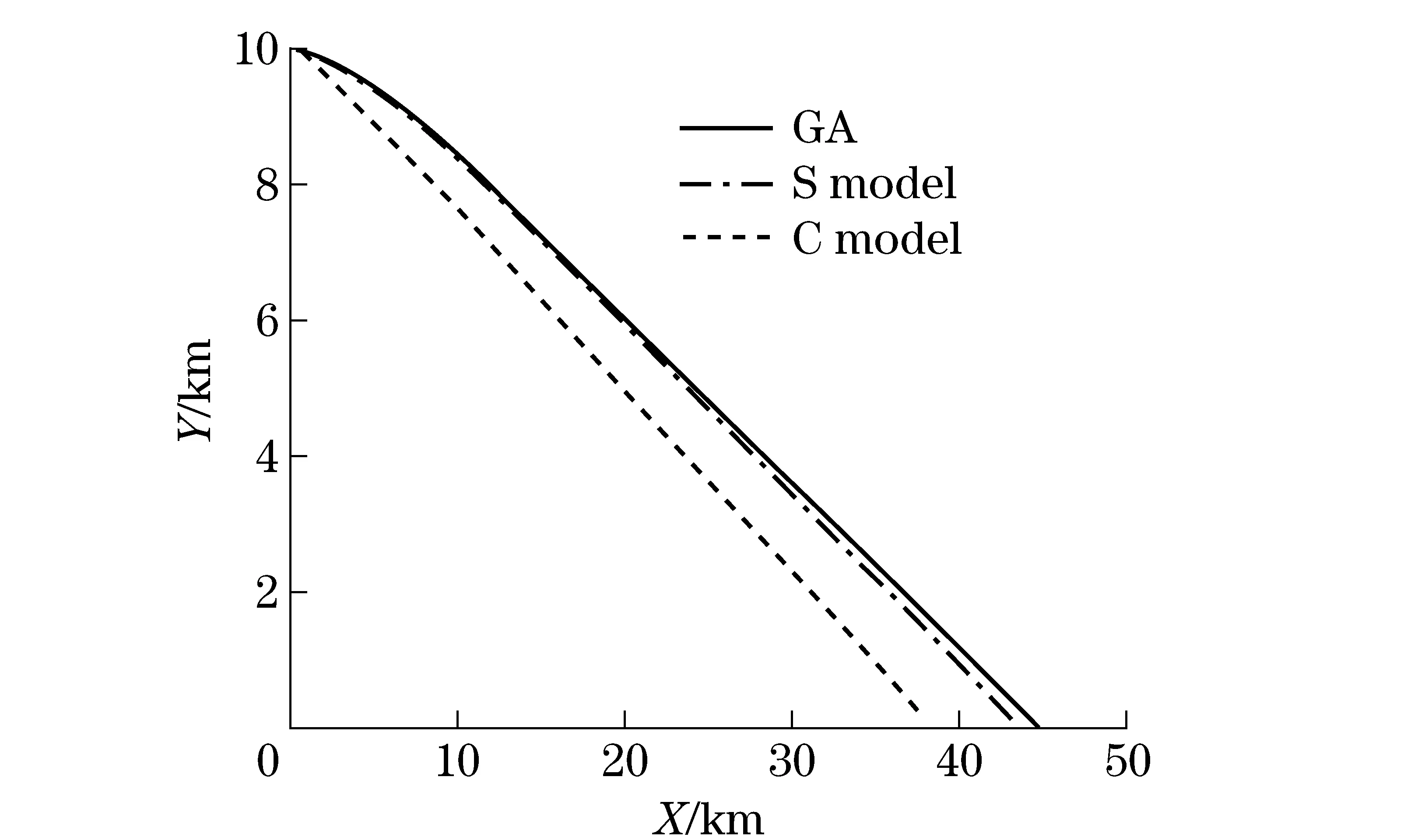
Fig.3 Distance of ballistic trajectory contrast of genetic algorithm, complicated model, simplify model

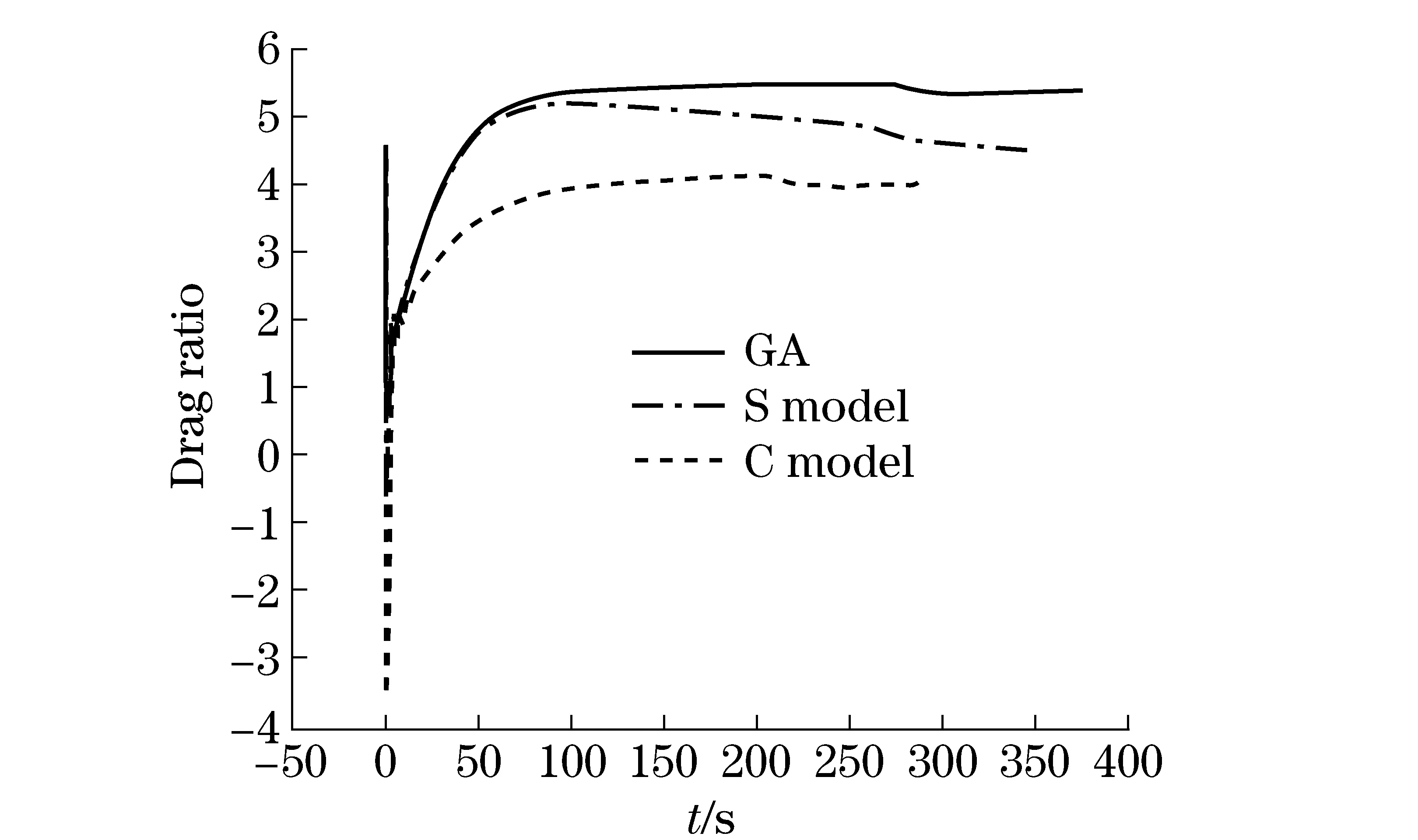
Fig.4 Drag ratio contrast of genetic algorithm, complicated model, simplify model

4 Conclusion

Inthispaper,threedifferentsolutionsofglidingaircraftoptimalcontrolwereinvestigated.Simplemodelplan’sattitudeanglesarestableanditcangetananalyticsolution.Analyticsolutionofoptimalcontrolincomplicatedmodelishardtogetthereforewechangedittoanumericalvaluesolution.Thethirdmethodisthatcomplicatemodelplancombinedwithageneticalgorithm,whichhaveagoodeffectofrealtimesearching.Theincreaseddistanceeffectisthebestamongthethreemethods.Thisalgorithmgivesoutawaytocalculatecomplicatemodel’soptimalanalyticsolution.

[1] Tang Shantong. Summary of the vehicle trajectory optimization and guidance law[J]. Modern Defence Technology,2002,30(1):33-37.

[2] Liu Li, Li Huaijian. The project trajectory optimization of airborne dispenser and the design of trajectory database[J]. Journal of Projectiles, Rockets, Missiles and Guidance, 2004,24(3):61-64.

[3] Xue Xiaozhong, Sun Chuanjie. Optimization design for the ballistics of simply guided bombs[J]. Acta Armamentarii,2004,25(3):377-378.

[4] Li Xiang, Liu Chang’an. Analysis and optimum design of the dive trajectory for a cruise missile[J]. Transactions of Beijing Institute of Technology,2006,26(9):774-776. (in Chinese)

[5] John T Betts. Very low-thrust trajectory optimization using a direct SQP method[J]. Journal of Computational and Applied Mathematics, 2000,120:27-40.

[6] Zhou Hao,Chen Wanchun. Optimization of glide trajectory for a hypersonic vehicle[J]. Journal of Beijing University of Aeronautics and Astronautics,2004,27(5):971-973. (in Chinese)

[7] Li Feng,Wang Haiying. A grouping algorithm based on genetic algorithm[J]. Journal of Changchun University of Technology,2013,34(2):215-217. (in Chinese)

[8] Cao Yongchun,Shao Yabin. A new clustering method based on grouping genetic algorithm[J]. Journal of Xihua University,2013,32(1):40-43. (in Chinese)

[9] Wang Hejun. A novel adaptive mutative scale optimization algorithm based on chaos genetic method and its optimization efficiency evaluation[J]. Journal of Central South University, 2012,19:2554-2560. (in Chinese)

[10] Han Peng, Shan Jiayuan, Meng Xiuyun. Re-entry trajectory optimization using a multiple-interval Radau pseudospectral method[J]. Journal of Beijing Institute of Technology, 2013, 22(1): 20-27.

(Edited by Wang Yuxia)

10.15918/j.jbit1004- 0579.201524.0205

TJ 765 Document code: A Article ID: 1004- 0579(2015)02- 0169- 04

Received 2013- 11- 05

Supported by the National Natural Science Foundation of China(11172071)

E-mail: 353057890@qq.com