桥梁施工监控中实测应力计算方法及MALAB实现

王莹峰

（重庆交通大学 土木建筑学院，重庆400074）

桥梁施工监控是桥梁施工的重要组成部分，在施工监控过程中，应力测试一直是监控的核心工作之一。施工过程中，准确的应力测试是判断桥梁安全与否和施工质量最主要的依据。然而现阶段施工过程中实测应力的计算一直没有行之有效的方法，其主要原因有以下两个方面:1）应力测试需通过应变测试实现，施工实测应变包含两部分，一部分为主要由加载时初始应变产生的应力应变，另一部分为主要由温度和收缩产生的非应力应变。如何从测得的应变中剔除非应力应变得到应力应变，这是应力测试的难点；2）混凝土具有徐变特性，如何在分阶段施工的梁体中计入徐变对实测应力的影响，这是应力测试的另一难点。因此，若不解决实际应力测试中的以上两个难点，应力计算结果与梁体实际受力情况将出现较大偏差。

作者结合在施工现场监控的技术积累，通过对混凝土实测应变构成和影响机理的分析总结出桥梁施工监控中考虑混凝土温度、收缩和徐变影响的实测应力计算方法，进一步完善了混凝土应力的实测技术。并且将算法编成MATLAB程序应用于巴中市东门大桥的实测应力计算，提高了计算结果的准确度，取得了良好的实际效果。

1 考虑混凝土温度和收缩影响的实测应变修正

当前施工监控中常使用的应变传感器其原理都是通过传感器与埋设点梁体具有一致的物理伸长量或缩短量来反映梁体应变，而此应变中包含的非应力应变不会在梁体中产生应力，必须将其剔除。根据1990年CEB－FIP标准规范，在时刻τ承受单轴向、不变应力为σ0（τ）的混凝土构件，在时刻t的总应变ε（t）可分解为

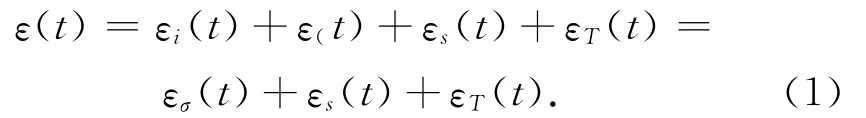
式中:εi（t）为加载时初始应变；εc（t）为在时刻的徐变应变；εs（t）为收缩应变；εT（t）为温度应变；εσ（t）为由应力引起的应变，即应力应变。

在剔除由收缩应变εs（t）和温度应变εT（t）构成的非应力应变后，应力应变可表示为

1.1 混凝土温度应变的计算

工程中常采用的裸埋式钢弦应变计附带温度记录功能。在应变计安装完成，梁体稳定、水化热基本散尽后的t0时刻读取应变计的初始应变ε初，某阶段施工完成后读取t时刻应变ε测，由于应变计埋入梁体内，可以完全传导梁体温度湿度和反映混凝土自由体积应变，Δε测＝ε测－ε初＝ε（t）即为t0→t时间段的总应变。

梁体混凝土的线膨胀系数和应变计钢弦的线膨胀系数是不一致的，t0时刻的梁体温度T0与t时刻的梁体温度Tt存在温度差值，此差值产生的温度应变εT（t）隐含于总应变ε（t）中，需要剔除。εt（t）可按下式计算

式中:εt（t）为t时刻梁体温度应变；Tt为t时刻梁体温度；T0为t0时刻梁体温度；αc为钢筋混凝土的线膨胀系数；αs为钢弦的线膨胀系数。

1.2 混凝土收缩应变的计算

混凝土收缩应变变化规律较为复杂，要得到可靠的收缩应变随时间变化的资料，必须通过试验对混凝土的收缩应变进行实测。通过查实测资料便可得到混凝土t0时刻的收缩应变εs（t0）与t时刻的收缩应变εs（tt），从而计算t0→t时间段的收缩应变εs（t）

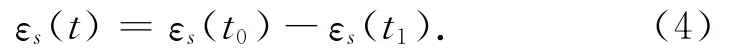
若无实测资料，可假定收缩应变的发展进程与徐变相似，即

则εs（t）可表示为

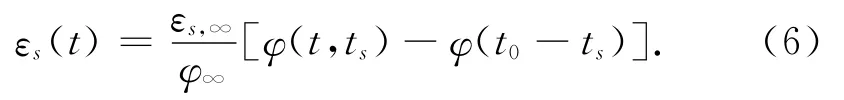
式中:εs（t）为t时刻梁体收缩应变；εs，∞为收缩应变终值，时间取极大值计算；φ∞为徐变系数终值，时间取极大值计算；φ（t，ts）为ts→t时间段徐变系数；φ（t0，ts）为ts→t0时间段徐变系数；ts为收缩开始时的混凝土龄期，可假定3～7d。

收缩应变和徐变系数根据《公路钢筋混凝土及预应力混凝土桥涵设计规范》（下文简称《规范》）相关公式计算。

2 混凝土实测应力的计算

现代的大跨度预应力混凝土桥梁通常采用双向或三向预应力技术，施工中的压应力控制指标一般为0.5倍抗压强度，在此工作应力下，混凝土的徐变应变与应力基本呈线性关系，分阶段施加应力所产生的阶段应变量可采用叠加原理计算。得到阶段应变量后，便可进行实测应力的计算。

2.1 考虑徐变影响的混凝土实测应力应变的计算

根据叠加原理，对于在τ0时刻施加初应力σ（τ0），又在不同的时刻τi（i＝1，2，…，n）分阶段施加应力增量Δσ（τi）的混凝土，其在以后任何时刻t考虑徐变影响的应力应变εσ（t）可表示为

式中:E′（τi）称为混凝土的应力应变模量，亦即等效弹性模量。Ε′（τi）应取当前阶段加载开始至加载结束时间段中点的等效弹性模量，对于紧凑施工的大跨径预应力桥梁而言，每阶段施工时间延续不长，为方便计算，可取加载开始时的等效弹性模量进行计算。对于不同龄期不同加载时段的等效弹性模量需通过徐变试验确定。若无实测徐变数据，t时刻应力应变εσ（t）可表示为

2.2 混凝土实测应力的计算

在完成对实测应变的温度、收缩和徐变影响修正后，便可进行实测应力的计算。为使实测应力变化历程真实反映分阶段加载过程，可将εσ（t）结合施工阶段分为对应的n个时段，各时段应变变量分别为εσ1，εσ2，…，εσn，各时段应力变量分别为Δσ1，Δσ2，…Δσn，则有

对于测试数据包含了两个或三个应力方向的应变，可根据广义虎克定律把实测应变转换成单轴应变，再用上述方法进行实测应力计算。

3 实测应力算法的MATLAB实现

大跨度预应力混凝土桥梁在施工过程中，需要进行应力监控的断面多，断面所布设的测点也多，每个施工阶段也可能进行多次实测应变数据的采集，加之算法包含多次迭代，实际计算具有相当的复杂性，这大大增加了实测应力的计算难度，降低了计算结果的准确性。MATLAB为当今国际公认的优秀数值计算和仿真分析软件，其与Excel具有良好的交互性。实际工程应用中，可以方便地在Excel中完成原始测量数据的记录和预处理，再将相关数据导入编好程序的MATLAB中进行计算。

3.1 实测混凝土应力计算的步骤

根据前文对实测混凝土应力计算方法的分析，实际计算可按下列步骤进行:

1）建立计算施工阶段k的k×k维上三角时间关联矩阵（t＿rel），存储tm→tn时间跨度，m＝1，2，…，k，n＝1，2，…，m；

2）计算施工阶段k的温度应变和收缩应变，对原始实测应变进行去非应力应变处理，将得到的应力应变存储入k×k维对角矩阵（stra＿rev）；

3）计算tm→tn时间跨度内的有效弹性模量，得到有效弹性模量上三角矩阵（MOE＿a），存储在时间关联矩阵的相应位置；

4）计算1阶段荷载应力 Δσ1＝E′（1，1）εσ1，计算1阶段荷载对后继tn→t1时间段应变影响:εσ（1，n）＝

6）循环（5）步骤，直至到第k个施工阶段结束；

8）将有效弹性模量矩阵对角线上的每一个元素与应力应变变量矩阵对角线上的每一个元素相乘并求和，得到施工阶段k的实测应力值，即

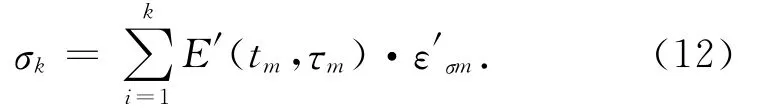
3.2 实测混凝土应力计算的MATLAB实现

下面给出计算方法的程序流程图如图1所示，MATLAB主程序代码如下:

图1 程序流程图

4 应用实例

巴中市东门大桥主桥为（68＋120＋68）m矮塔斜拉桥，宽32.5m。主梁采用单箱三室大悬臂变截面预应力混凝土连续箱梁，混凝土强度等级C55，支点梁高4.625m，跨中梁高2.625m，从支点起25m范围内梁高按二次抛物线变化，设计荷载为公路I级，采用悬臂挂篮施工，在施工过程中对主梁进行应力监控测试。根据本桥受力特点，选取悬臂根部、中部和中跨跨中9个截面布点，采用附带温度记录功能的埋入式钢弦应力计。

以悬臂根部应力监控截面为例，0#节段浇筑前预埋好应力计，待混凝土稳定、水化热基本散尽后即第3天记录初始值，用以消除应力计初始偏差，并以此为起点计算徐变影响。后继节段分混凝土浇筑完成和纵向钢绞线张拉完成两个应力测试阶段，有斜拉索张拉节段新增斜拉索张拉完成测试阶段。因为缺乏徐变试验实测数据和混凝土瞬时弹量实测数据，根据《规范》计算徐变系数，用以计算收缩应变和等效弹量。2#墩小里程断面顶板测点在各监控阶段的实测数据和考虑不同修正因素条件下计算数据的对比见表1。表1中，σ（k）表示按本计算方法计算的应力值，σ（kT）表示不进行温度修正计算的应力值，σ（kS）表示不进行收缩修正计算的应力值。不同影响因素下计算数据的对比见图2。图3为该截面顶板测点和底板测点在各主要施工阶段的计算实测应力与理论应力的比较结果。

表1 监控点的实测数据和计算数据

图2 不同影响因素下计算数据的对比

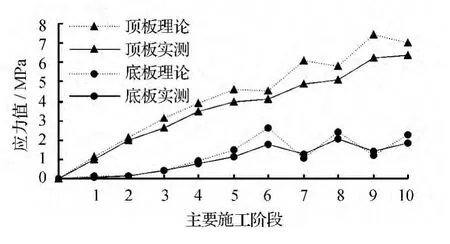
图3 实测应力与理论应力比较

5 结束语

1）通过采用非应力应变处理后的修正实测应变和按龄期调整的等效弹性模量进行实测应力的计算方法是可行，其计算结果精度满足工程需求。

2）温度和收缩对实测应力计算的结果均有较大影响。实测应变若不进行温度修正，则计算结果普遍偏小，若不进行收缩修正，则结果普遍偏大。两个影响因素中，温度的影响幅度更大，尤其是施工初期，原因主要是累计应变量小，温度引起的非应力应变占较大比重。为了减少温度给计算结果带来的影响，应变计的初值记录时间宜选取在水化热基本散尽的清晨，后继节段的测量时间也宜选取在初值记录的同一时段。混凝土在浇筑完成的前30d，收缩对仪器测读值影响很大，必须予以考虑。

3）梁体进入长悬臂施工阶段后，实测应力值和理论值之间的差值一般会逐步加大，其原因一方面为计算选取材料参数和实际施工材料参数的差异，这种差异产生的误差会在迭代过程中叠加，可进行相关材料参数识别后修改计算模型以提高计算准确度，另一方面是应变滞后性的影响。在长悬臂施工阶段，纵向钢绞线较长，管道传力受阻，应变反应较前期施工阶段“迟钝”，产生应变滞后现象。应变滞后也可合理解释实测应力曲线较理论应力曲线变化更为平滑的现象。

4）MATLAB具有较高的编程效率，强大的矩阵计算能力，对此实测应力算法极其适用。

［1］ 曾德荣.桥梁施工监测应力真值分析方法［J］.重庆交通学院学报，2005，24（6）:18－24.

［2］ 江湧，荆秀芬，石雪飞.桥梁施工监控测试中混凝土实测徐变应变的计算方法［J］.桥梁建设，2005（sup）:145－147.

［3］ 赵俊杰.大跨连续刚构施工过程中的收缩徐变分析控制［D］.上海:同济大学，2000.

［4］ 0－7277－1696－4，CEB－FIP MODEL CODE 1990 ［S］.London:Thomas Telford Services Ltd，1993.

［5］ 项海帆.高等桥梁结构理论［M］.北京:人民交通出版社，2001.

［6］ 中华人民共和国交通部.公路钢筋混凝土及预应力混凝土 桥 涵 设 计 规 范 （JTG D62－2004）［S］.978－7－114－05052－7.北京:人民交通出版社，2004.

［7］ 朱伯芳.有限单元法原理与应用［M］.北京:中国水利水电出版社，2009.

［8］ 黄国兴，惠荣炎，王秀军.混凝土收缩与徐变［M］.北京:中国电力出版社，2012.