使用GRACE时变重力场中的维纳滤波

郭飞霄，苗岳旺，肖 云

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054；3.测绘信息技术总站，陕西 西安，710054



使用GRACE时变重力场中的维纳滤波

郭飞霄1,2，苗岳旺3，肖 云1,2

1.西安测绘研究所，陕西 西安，710054；2.地理信息工程国家重点实验室，陕西 西安，710054；3.测绘信息技术总站，陕西 西安，710054

GRACE时变重力场模型误差随着阶数增大而迅速增大，必须采用滤波进行空间平滑。本文利用GRACE时变重力场模型数据计算全球陆地水储量变化，分析了维纳滤波对反演结果的影响，并与不同半径高斯滤波反演结果进行了对比。实验结果表明：维纳滤波是一种低通滤波，滤波系数仅与时变重力场模型噪声特性相关；维纳滤波能够有效消除全球陆地水储量变化反演结果中的南北条带误差，反演结果与半径400km高斯滤波反演结果相当。

GRACE卫星，时变重力场，维纳滤波，水储量变化，卫星重力

1 引 言

地球重力场及其时变效应反映了地球表层及内部的物质分布和变化。当前，全球性环境问题如海平面上升、极地冰川融化等与地球表层的物质迁移紧密相关。因此，研究地球系统的质量迁移和重新分布对监测全球环境和气候变化具有重要意义。2002年3月，GRACE卫星的成功发射开创了高精度全球重力场观测与气候变化试验新纪元，该计划旨在恢复高精度和高分辨率全球静态重力场，并估计地球重力场的时变特征。GRACE卫星Level-2数据能够提供空间分辨率约为400km、时间分辨率约为30天的地球重力场时变模型。Wahr等建立了利用时变重力场模型估计地球表层质量变化的球谐系数算法[1]，目前已广泛应用于[2-5]陆地水储量变化、地震同震、海洋环流和冰川融化等领域的研究。

GRACE时变重力场模型受卫星轨道误差、星间测距误差、加速度计误差影响以及高阶项误差等影响，球谐系数法恢复地球时变重力场结果表现为严重南北方向条带误差，因此必须进行滤波处理。Wahr等提出了各向同性的高斯滤波方法，对时变重力场模型阶项进行降权滤波[1]；张子占等提出了扇形滤波方法，该方法对时变重力场模型的阶项和次项同时应用一次高斯滤波，其本质是一种非各向同性的高斯滤波[6]。但不论是高斯滤波还是扇形滤波，计算时都需要选取合适的滤波半径。如果滤波半径过大，对模型空间分辨率的牺牲程度也越大；滤波半径过小，则无法有效消除条带误差，给地球物理信号识别带来困难。因此，对于GRACE时变重力场空间滤波，要在空间分辨率和噪声减小之间进行优化处理。Sasgen等提出了针对时变重力场的维纳滤波算法，与高斯滤波不同的是，维纳滤波仅与期望信号和噪声的阶方差有关，能够提高信噪比[7]。本文对GRACE时变重力场维纳滤波算法进行了推导分析，将维纳滤波应用球谐系数法，反演了全球陆地水储量变化，并与采用高斯滤波方法反演结果进行了对比分析，总结分析了维纳滤波算法的特点。

2 维纳滤波基本原理

维纳滤波是线性卷积滤波，其输出信号y(Ω)由实际测量信号x(Ω)和滤波函数h(Ω)进行空间卷积得到：

(1)

(2)

(3)

Ylm(Ω)=Plm(cosθ)eimλ

(4)

(5)

维纳滤波满足以下条件：

(1)实际输出信号y(Ω)与期望输出信号y′(Ω)满足最小二乘准则，即：

(6)

由Parseval等式，式(6)可写为：

(7)

(2)测量信号x(Ω)由真实信号s(Ω)和噪声n(Ω)组成：

x(Ω)=s(Ω)+n(Ω)

(8)

(3)信号s(Ω)和n(Ω)不相关，即：

(9)

(4)期望输出信号y′(Ω)与未污染的原始信号s(Ω)等价。

在以上条件下，最小二乘准则E2可写成如下形式：

(10)

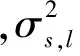
(11)

式中，{Cs,lm,Ss,lm}和{Cn,lm,Sn,lm}分别为信号s(Ω)和噪声n(Ω)的球谐模型展开系数。因此，式(10)就是求解hl使得E2最小。令E2对hl求偏导数，并令偏导数等于0，可得：

(12)

hl即为第l阶维纳滤波系数。从式(12)可以看出，当噪声可以忽略时，hl为单位值1；当噪声占主要成分时，hl为0。因此，式(12)给出了在两个极端情况下的最佳过渡。

3 利用GRACE时变重力场数据确定维纳滤波系数

维纳滤波是各向同性滤波，滤波系数仅与信号和噪声的阶方差相关。利用式(12)求解维纳滤波系数，需要分别估计重力信号和噪声的阶方差。但是，如果没有额外信息或者假设条件，便无法从测量信号中估计这两个值。不过，从GRACE数据可以获取额外信息，来帮助估计重力信号和噪声的阶方差。

图1 GRACE时变重力场模型平均阶方差

图1所示为GRACE时变重力场模型的平均阶方差，以大地水准面高形式表示，所示结果为2004年1月至2010年12月时变重力场模型统计结果。平均阶方差计算如下：

(13)

(14)

Sasgen等认为时变重力场模型的低阶项(l< 20)主要是地幔以下地球重力场时变信号的体现，而高阶项(l> 30)则反映了GRACE数据的噪声信息；位于这两者之间(20≤l≤30 )则是信号和噪声的混合，体现了地球表层的陆地水储量和海洋质量的变化[7-8]。地球重力场时变信号可由式(15)所示的函数近似表达[7]：

(15)

(16)

对式(15)两边同时取以10为底数的对数，如式(16)所示。由于低阶项部分(l<20)主要是地球重力场时变信号的体现，因此，参数a与参数b可利用平均阶方差低阶项的数据进行最小二乘估计求得。对高阶项部分，噪声信息占主要部分。噪声部分在以10为底数的对数形式下，可用线性函数[7]近似表达：

(17)

4 实验分析

实验中，GRACE时变重力场模型数据采用德国地学中心(GFZ)发布的Level-2Realease05数据，时间跨度为2004年1月至2010年12月。计算时对GRACE时变重力场模型截断至60阶，低阶带谐项C20项采用SLR观测得到的C20项进行替代[9]。先将所有GRACE时变重力场模型求平均值作为稳态背景场，再计算每个月时变重力场模型相对于稳态背景场的改变量，分别采用维纳滤波、高斯滤波，按照式(18)计算全球陆地水储量变化。

(18)

其中，Δh为陆地水储量变化的等效水柱高度，{ΔClm,ΔSlm}为球谐系数的改变量，kl为l阶负荷勒夫数，a为地球平均半径，ρa为地球平均密度，ρw为水密度，Wl为滤波系数。

高斯滤波的滤波半径分别取300km、400km和500km，滤波系数Wn按式(19)计算。其中，b=ln2/[1-cos(r/a)]，a为地球平均半径，r为滤波半径。

(19)

由GRACE时变重力场模型数据对时变重力场信号和噪声部分按照第3节所述方法进行拟合，所得结果如图2所示。图2中，红色线为平均阶方差，蓝色线为噪声拟合值，绿色线为时变重力场信号拟合值。所得拟合参数分别为：a=1.291，b=2.382，c=-3.347，d=0.044。

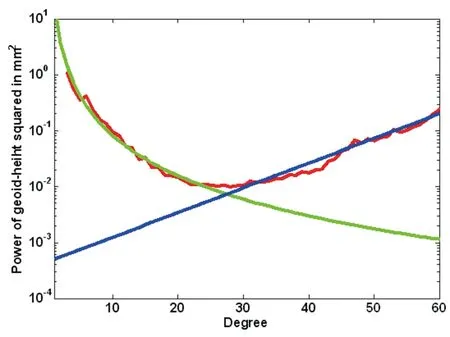
图2 信号和噪声阶方差谱(红色为时变重力场模型平均阶方差，蓝色为噪声部分拟合值，绿色为时变重力场信号拟合值)

下面以2010年4月全球陆地水储量变化反演结果进行分析，如图3所示。其中，图3(1)～(4)为采用维纳滤波、半径分别为300km、400km和500km高斯滤波的全球陆地水储量变化反演结果。从图3可以看出，采用半径300km高斯滤波，虽然大尺度的全球陆地水储量变化信号明显，但反演结果中南北方向条带误差也非常明显；而采用维纳滤波和半径400km高斯滤波，噪声误差都得到了有效控制，反演结果中对南北方向条带误差抑制效果显著，大尺度的水文信号更加清晰；半径500km高斯滤波反演结果中，南北方向条带状误差基本消除，但反演结果分辨率有所下降，局部区域陆地水储量变化信号减弱。进一步对比图3(1)和图3(3)可以看出，维纳滤波和半径400km高斯滤波都基本消除了条带误差，反演结果吻合程度较高，但维纳滤波反演陆地水储量变化信号更强。

图3 2010年4月全球陆地水储量变化(单位：cm)

图4所示为不同滤波半径高斯滤波和维纳滤波系数的比较结果。从图4可以看出：(1)随着滤波半径增加，对于同阶项高斯滤波系数更小，并且高斯滤波系数收敛速度更快；(2)维纳滤波和高斯滤波都是低通滤波，低阶项所占比重大，随着阶数的增加，滤波系数迅速减小；(3)与高斯滤波相比，维纳滤波在低阶项部分(l<20)的滤波系数权值较大，在高阶项(l>30)的滤波系数迅速减小收敛。而GRACE时变重力场模型低阶项主要是重力信号，高阶项部分则主要反映了噪声误差。因此，与高斯滤波相比，维纳滤波能够更好地反映时变重力信号，这与图3所示全球陆地水储量反演结果相符。

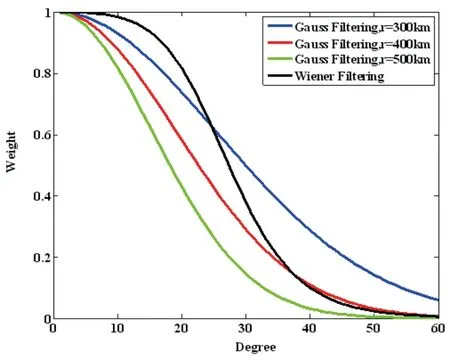
图4 不同半径高斯滤波和维纳滤波系数

5 结 论

由于GRACE时变重力场模型高阶项部分存在较大误差，利用该时变重力场模型反演陆地水储量变化时表现为严重的条带误差，因此必须采用滤波进行空间平滑。维纳滤波是基于信号和噪声的平均阶方差谱建立信号和噪声函数，其提高了低阶项权重，同时降低了高阶项权重。由实验结果可得出以下结论：(1)维纳滤波是一种低通滤波，与高斯滤波不同，维纳滤波不需要确定滤波半径，滤波系数仅与时变重力场模型的噪声特性有关；(2)维纳滤波能够有效抑制条状误差，全球陆地水储量反演结果与半径400km的高斯滤波反演结果相当；(3)与高斯滤波相比，维纳滤波系数在低阶项权重更大、高阶项权重更小，因此能够更好地反映时变重力信号。

[1]Wahr J, Molenaar M, Bryan F.Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE[J]. J.Geophys.Res, 1998, 103(B12):30205-30229.

[2]李琼，罗志才，钟波．利用GRACE时变重力场探测2010年中国西南干旱陆地水储量变化[J],地球物理学报， 2013,56(6):1843-1849.

[3]王武星，石耀霖，顾国华等．GRACE卫星观测到的与汶川Ms8.0地震有关的重力变化[J]．地球物理学报，2010, 53(8):1767-1776.

[4]蒋涛，李建成，王正涛等．联合Jason-1与GRACE卫星数据研究全球海平面变化[J].测绘学报，2010，39(2)：134-149.

[5]朱广彬，李建成，文汉江等．利用GRACE时变位模型研究南极冰盖质量变化[J].武汉大学学报信息科学版，2009，34(10)：1185-1190.

[6]Zi-zhan Zhang, B.F.Chao, Yang Lu, et al.An effective filtering for GRACE time-variable gravity: Fan filter [J]. Geophysical Research Letters, 2009, 36(17):1397-1413.

[7]Sasgen I, Martince Z, Fleming K.Winener optimal filtering of GRACE data [J]. Stud.Geophys.Geod.2006,50:499-508.

[8]Wahr J, Swenson S, Zlotnicki V, et al.Time-variable gravity from GRACE: First results[J].Geophys.Res.Lett,2004,31(11):293-317.

[9]J L Chen，M Rodell，C R Wilson，et al．Low degree spherical harmonic influences on Gravity Recovery and Climate Experiment(GRACE) water storage estimates [J].Geophysical Research Letters, 2005,32(14):57-76.

Wiener Filtering in Use of GRACE Time-variable Gravity Field

Guo Feixiao1, 2,Miao Yuewang3,Xiao Yun1, 2

1. Xi’an Research Institute of Surveying and Mapping, Xi’an 710054, China 2. State Key Laboratory of Geo-information Engineering, Xi’an 710054, China 3.Technical Division of Surveying and Mapping，Xi’an 710054, China

The error of the GRACE time-variable gravity model increases with the increasing of degree. This problem must be solved by spatial smoothing. Global water storage variation is recovered by GRACE time-variable gravity data. The influence of Wiener filtering on the inversion result is analyzed and compared with Gauss filtering of different radius. The results show that Wiener filtering is a low-pass filtering, and weight of Wiener filtering only relys on the noise character of GRACE time-variable gravity models. Stripe error in global water storage variation recovery is removed effectively by Wiener filtering. The inversion result is consistent with radius of 400km Gauss filtering.

GRACE satellites, time-variable gravity field, Wiener Filtering, water storage variation, satellite gravimetry

2015-01-27。

国家自然科学基金资助项目(41374083)，国家973计划资助项目(2013CB733303)，大地测量与地球动力学国家重点实验室开放基金资助项目(SKLGED2013-3-3-E)。

郭飞霄(1988—)，男，硕士研究生，主要从事重力测量数据处理方面的研究。

P228

A