水准测量中海潮负荷改正的计算
徐新强,赵德军
测绘信息技术总站,陕西 西安,710054
水准测量中海潮负荷改正的计算
徐新强,赵德军
测绘信息技术总站,陕西 西安,710054
本文详细推导了由海潮模型和格林函数卷积积分计算倾斜负荷效应的公式,给出了切实可行的计算方法;同时,利用NAO99b全球海潮模型,采用Farrell积分格林函数法,计算了部分地区倾斜负荷潮及部分沿海水准的海潮负荷改正值。本文给出的计算方法适合于高等级水准计算。
水准;海潮负荷(OTL);倾斜负荷;海潮模型;格林函数
1 引 言
固体地球除受引潮力的直接作用而发生垂直和水平位移外,还受海洋潮汐产生的周期性负荷的作用而发生垂直和水平位移。研究表明,海潮负荷效应(Ocean Tidal Loading,OTL)包括[1]:(1)海水的直接引力;(2)在海水引力和压力的作用下产生的地壳变形;(3)上述变形使得质量重新分布而产生的附加位。
文献[2,3]用CSR系列海潮模型计算了高等级水准路线上的海潮负荷改正,并得出在我国近海地区,水准环闭合差能够得到改善的结论。2006年发布的国标中明确要求一、二等水准测量数据处理时要进行OTL改正,并建议使用CSR4.0+CS(China Sea)或精度更高的海潮模型[4],但对南北、东西倾斜分量的计算仅给出2个基本计算公式,对其中涉及到的大量参数的计算没有描述,缺乏可操作性。鉴于此,本文给出了实用、切实可行的计算方法。
2 倾斜负荷潮计算方法
高精度水准计算中,海潮改正公式为[4]:
L=(ξcosA+ηsinA)S
(1)
式中,ξ、η分别为海潮负荷引起的计算点的南北、东西倾斜分量;A为水准路线方向的方位角;S为测段长度。对于水准路线来说,A,S是已知的,关键是如何求倾斜分量ξ和η。
倾斜负荷潮严格计算式如下[1,5,6,7]:
(2)
其中:
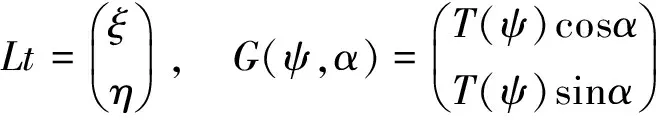
式中,θ、λ分别是负荷点的余纬和经度;t是世界时;R是地球平均半径;ρ是平均海水密度;α是计算点到负荷点(θ,λ)的方位角;ψ是计算点到负荷点的球面角距。G(ψ,α)是质量负荷格林函数,T(ψ)是倾斜负荷格林函数。瞬时海潮高H(θ,λ,t)可以分解成调和分潮之和[1]:
(3)
其中:
Hcp(θ,λ)=ζp(θ,λ)cosδp
Hsp(θ,λ)=ζp(θ,λ)sinδp

(4)
式(4)即文献[4]中的(D.22)式,其中:
(5)
而:
tanβp=LSp/LCp
表1 主要调和分潮的角速度,单位:°/h

分潮角速度M228.984S230.000N228.439K230.082K115.041O113.942P114.958Q113.405Mf1.098Mm0.544Ssa0.082
天文辐角χp是天文引数的线性组合,通过下式来计算[1]:
χM2=2h-2s
χS2=0
χN2=2h-3s+q
χK2=2h
χK1=h+90°
χO1=h-3s+q-90°
χMf=2s
χMm=s-q
χSsa=2h
式中,天文引数s、h、q分别表示月亮的平黄经、太阳的平黄经和月亮升交点经度[1]:
h=279.69668°+36000.76892°T-0.00030°T2
s=270.43659°+481267.89057°T+0.00113°T2
q=334.32956°+4046.03403°T-0.01032°T2式中,T为儒略世纪数,从1973年起算。
3 数值计算
3.1 海潮模型的选择
海潮负荷引起的倾斜精度主要取决于海潮模型、格林函数以及数值积分方法[8,9]。NLOADF提供了多种地球模型的格林函数,并且采用完全高斯数值积分的方法计算式(5),因此,倾斜负荷的精度取决于海潮模型的精度和分辨率[9]。随着卫星测高技术的发展,先后出现了CRS3.0、CRS4.0、AG95、GOT、NAO、FES2004、TPXO7等多种海潮模型。文献[11]利用304个全球验潮站、137个中国东海验潮站和63个南海验潮站多年的观测资料,分析对比了几种目前具有代表性的海潮模型,认为NAO99b在中国海域精度最高。文献[12]用GPS观测资料分析对比了多种海潮模型,认为NAO99b 在我国黄海、东海、南海和印尼海域具有较高精度。NAO99b是日本国家天文台基于二维非线性浅水方程,采用Blending方法同化日本韩国沿岸验潮站和5年T/P沿轨海面高数据建立的全球以及日本周边局部海潮模型[11]。
3.2 倾斜负荷潮计算
表2 M2分潮东西向倾斜分量,单位:振幅 nrad,相位°

台站NAO99bCSR4.0+CS振幅相位振幅相位BJFS2.668-130.33.818-97.3SHAO69.20265.368.65862.1WUHN5.139-9.65.848143.7XIAM75.83084.458.214126.2GUAN9.700-5.69.815145.0KMIN3.809-60.24.211-145.8URUM1.205-46.71.178-131.0QION19.13135.723.963105.7YONG11.433-39.710.354-176.3
为了与文献[6]做对比分析,采用标准的GBA平均地球模型计算部分地壳运动观测网络台站,M2分潮东西方向倾斜负荷效应的影响(即η),采用NAO99b模型计算,其中CSR4.0+CS模型计算结果来自文献[6]。注意:按式(2)计算的倾斜负荷效应(ξ,η)的振幅分别以南、西方向为正,振幅的单位是nrad(即10-9弧度),相位的单位是度。由表2可知OTL对沿海地区倾斜潮的影响特别显著,可达数十nrad;对内陆的影响在几nrad量级,如SHAO的振幅达到69.202nrad,而URUM则只有1.205nrad。不同海潮模型的计算结果有一定的差异,这是由于复杂的近海海岸形状、海底地形和特殊的海湾条件导致海潮模型有一定差异[1]。

图1 永兴岛倾斜分量随时间变化图
由式(4)可知,已知测站的位置和观测时间,将各个分波的倾斜负荷叠加就能算出海潮对测站的倾斜分量。图1给出了永兴岛的倾斜分量时间序列图,时间从2013年7月1日至7月30日共720小时。上图为东西倾斜分量,下图为南北分量。
3.3 水准测量中的海潮负荷改正
本文收集了国家海岛礁一期测绘工程沿海200多条二等水准测段数据,海潮模型采用NAO99b。海潮负荷改正与水准路线位置和观测时间有关,因此给出了水准测段往返测的OTL改正值(表3)。从中可以看出往测92.5%、返测93.7%的测段改正值小于0.05mm。往返测平均改正值的绝对值分别为0.019mm和0.023mm,由于此值已比其它系统误差改正值大(如视准轴误差、地球曲率改正),因此必须进行OTL改正。但是,OTL对水准路线改正值不太明显,因为水准测量中OTL改正一般只占到固体潮改正的10%[1]。
表3 水准测段往返测OTL改正值

改正值范围(mm)往测百分比往测百分比L≤-0.11.00.4-0.1
由式(1)知,改正值除了与ξ和η有关外,还与水准路线的方位角、测段长度和观测时间有关,因此,同一地区的测段及其改正值也有一定的差异。由于缺乏高等级的水准数据,本文没有计算海潮改正对水准环闭合差的影响,文献[3]认为海潮负荷改正对水准环闭合差的影响不大,一般在5mm以内。
4 结 论
通过理论分析和数值计算得出以下结论:
(1)OTL对倾斜影响的振幅可达到几nrad,沿海地区可达10nrad或更多,并且随测区离海洋的距离增加而减少,靠海洋越近则影响越大。同一地区的测段及其改正值也有一定的差异,这是因为改正值还与水准测段的方位角以及观测时间有关。
(2)不同海潮模型计算的倾斜影响间存在一定的差异,这与近海海岸线形状、海底地形和特殊的海湾条件等因素有关。有条件的情况下,尽量使用验潮站实测的海潮资料修正全球模型,或用实测数据评估全球海潮模型。
(3)虽然OTL改正值很小,但部分测段的改正值大于其它系统误差改正值,因此,高精度水准计算时必须加入OTL改正。
[1]中国科学院测量与地球物理研究所.固体潮论文集[M].北京:测绘出版社,1988.
[2]董鸿闻,陈士银,许大欣等.高精度水准测量的海潮负荷改正[J].测绘通报,2000,7(3):14-16.
[3]王文利,董鸿闻.用CSR4.0+CS模型计算海潮负荷改正[J].大地测量与地球动力学,2003,23(4):70-74.
[4]GB/T 12897-2006.国家一、二等水准测量规范[S].北京:中国标准出版社,2006.
[5]周江存,许厚泽,孙和平.中国台湾地区海洋负荷潮汐对重力、位移、倾斜和应变固体潮观测的影响[J].大地测量与地球动力学,2002,22(1):81-86.
[6]孙和平,周江存,许厚泽.中国地壳运动观测网络基准站倾斜固体潮观测中的海潮负荷信号改正问题[J].地球物理学进展,2001,16(3):21-39.
[7]周江存,孙和平.高精度GPS观测中的负荷效应[J].地球科学进展,2007,22(10):1036-1040.
[8]Bos M S,Baker T F.An estimate of the errors in gravity ocean tide loading computations [J].Journal of Geodesy,2005,79:50-63.
[9]Agnew D C.NLOADF: a program for computing ocean-tide loading. J Geophys Res, 1997, 102(B3):5109-5110.
[10]暴景阳,许军.中国沿岸验潮站潮汐调和常数的精度评估[J].海洋测绘,2013,33(1):1-4.
[11]李大炜,李建成,金涛勇.利用验潮站资料评估全球海潮模型的精度[J].大地测量与地球动力学,2012,32(4):106-110.
[12]赵红,张勤,黄观文.基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J].大地测量与地球动力学,2012,32(5):108-112.
Calculation of Ocean Tidal Loading Correction in Leveling
Xu Xinqiang,Zhao Dejun
Technical Division of Surveying and Mapping, Xi’an 710054, China
This paper deduces the tilt loading effects formulae in detail based on the convolution integration approach of ocean tidal model and Green's function, and it presents the practical computing algorithms. Besides, the tilt loading in some area are calculated using the integral method of Farrell's Green's function, which adopts global tidal model NAO99b, and the ocean tidal loading correction in part of coastal areas are calculated. The computing algorithms presented in this paper are suitable for high accuracy leveling data.
leveling; ocean tidal loading (OTL); tilt loading; ocean tidal model; Green’s function
2015-01-16。
国家863计划资助项目(2013AA122501)。
徐新强(1968—),男,高级工程师,主要从事大地测量数据处理及地球重力场的研究。
P312.4
A

