VK-Stokes核函数的性能分析
荣 敏,周 巍,吴富梅,任红飞
1.信息工程大学地理空间信息学院,河南 郑州,450052;2.西安测绘研究所,陕西 西安,710054;3. 测绘信息技术总站,陕西 西安,710054
VK-Stokes核函数的性能分析
荣 敏1,2,3,周 巍3,吴富梅2,任红飞2
1.信息工程大学地理空间信息学院,河南 郑州,450052;2.西安测绘研究所,陕西 西安,710054;3. 测绘信息技术总站,陕西 西安,710054
为了获取高精度大地水准面、克服重力数据不能实现全球覆盖所带来的问题,常应用修正Stokes核函数。它能改善标准Stokes核函数特性,使其在较小积分范围内达到较高计算精度。本文基于地球重力场位系数模型EGM2008,分析了修正核函数(VK-Stokes)特性及其远区截断误差。计算分析表明:在近区0.2°积分半径内,VK-Stokes与标准Stokes和WG-Stokes核函数值接近;但随着积分半径增加,VK-Stokes较标准Stokes核函数收敛更快,且其远区截断误差数值也相对较小。由此可见,应用VK-Stokes核函数,既可实现在较小积分范围内提高计算能力,又能抑制其远区截断误差影响。
大地水准面;Stokes核函数;VK-Stokes核函数;截断误差影响
1 引 言
应用Stokes公式计算大地水准面时,需要在全球范围内进行求解;但由于数据、成本和计算效率等原因,实现全球积分不太现实[1-15]。为了克服困难、提高计算精度和效率,学者们提出了多种改善方法。其中,将积分域划分为球冠(近区)和剩余部分(远区)两部分[5];再将重力异常值按照频谱划分为高频和低频两部分,用高精度地球重力场模型移去低频影响,对剩余重力异常采用Stokes公式进行解算。若直接采用标准Stokes核函数,可能会产生波长扭曲现象,因此需要修正标准Stokes核函数[5]。修正Stokes核函数,一则可以改变标准Stokes函数特性,二则还可使其远区截断误差迅速减小,最为理想的状态是其值为0。
修正Stokes核函数已在多个大地水准面计算实例中得以应用。2005年,A.Ellmann应用WG-Stokes函数和VK-Stokes核函数,在波罗的海沿岸地区进行了分析[13]。2011年,W.E. Featherstone等人在建立最新澳大利亚重力水准面模型AUSGeoid09时,对球面Stokes核函数(S-Stokes)、WG-Stokes和FEO-Stokes进行了应用分析[14]。2012年,Y.M. Wang等在美国重力大地水准面模型(USGG2009)建立中,采用了WG-Stokes核函数[15]。2012年,Huang Jianliang 综合了WG-Stokes和限阶次Stokes函数,提出新的修正核函数(MDBK),并将其应用于加拿大最新重力大地水准面模型建立[16]。2013年,傅露等结合DNSC08- CRA模型中的美国近海测高重力数据,分析比较了5种修正Stokes核函数的计算精度,认为修正Stokes核函数可有效改善计算精度[17]。为了进一步提高局部区域(似)大地水准面计算精度,更恰当地使用VK-Stoke核函数,本文分析了VK-Stokes函数特性及其远区的截断误差,并与标准Stokes和WG-Stokes核函数进行比较。
2 大地水准面差距计算
所谓大地水准面差距是指大地水准面与参考椭球面间的距离。通过大地水准面差距,可实现大地高与正高间的转化。大地水准面差距N的计算表达式为[1-2]:
(1)
式中,R为地球平均半径;γ0为正常重力;Δg为大地水准面上重力异常值;Ψ为计算点与积分点之间的球面角距;积分单元dσ=sinΨdΨdα;S(Ψ)表示Stokes函数。
将积分区划分为近区(σ0)和远区σ-(σ0),则有:
(2)
基于移去-恢复法,则有:
(3)
式中,NM为低阶位系数模型计算大地水准面差距;Δgres为用地球重力场模型移去长波项后,剩余重力异常值。
低阶位系数模型计算重力异常公式如下:
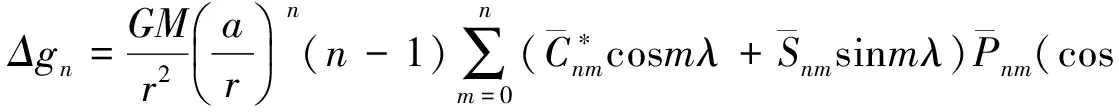
(4)

尽管采用移去-恢复法,基于地球重力场位系数模型移去长波项,但是剩余重力异常中还会时常存在残余长波信号。另外,剩余重力异常在有限积分范围内进行解算,其远区影响通常被直接忽略,引入了一定误差。考虑应用VK-Stokes核函数,对于解决上述问题有一定程度改善。
3 修正的Stokes核函数
3.1WG-Stokes核函数
WG-Stokes核函数是1969年由Wong和Gore给出,它是直接将球面Stokes核函数值剔除其低阶部分。用SWG(Ψ)表示WG-Stokes核函数,则有:
(5)
式中,Ls为截断阶次;Pn(cosΨ)为Legendre多项式。
或写成:
(6)
(7)

(8)
3.2VK-Stokes核函数
1987年,Vanicek和Kleusberg基于Molodensky思想修正了WG-Stokes核函数,使截断误差上限最小,给出了VK-Stokes核函数,其具体形式为:
式中,tn(Ψ0)为修正系数;Lm为修正阶次。
将上式改写为:
(10)
(11)

(12)

(13)
求解待定系数tn(Ψ0)(n=0,1……,Lm)时,若使截断误差上限最小,则必须令下式最小。
(14)

(15)
采用数值方法计算求解tn(Ψ0)。
4 远区截断误差
远区截断误差是指剩余重力异常的远区影响,其计算表达式为:
(16)
WG-Stokes核函数相应截断误差影响计算公式为:
(17)
VK-Stokes核函数相应截断误差影响计算公式为:
(18)
基于移去-恢复法,远区影响一般可由地球重力场位系数模型近似求得,其主要误差源于位系数误差和有限截断阶次引起的误差。位系数误差随模型建立而引入,为已知量。
5 实验分析
5.1 核函数特性分析
为了更好地应用VK-Stokes函数,基于EGM2008位系数模型,比较分析其与标准Stokes核函数以及WG-Stokes核函数,与截断阶次、修正阶次和积分半径间的关系,见图1(a)~(f)所示。图1(a)和(b)分别为近区、标准Stokes函数与截断并修正至20和120阶的WG-Stokes函数及VK-Stokes函数,随着积分半径变化的情况;图1(c)和(d)分别为远区、标准Stokes函数与截断并修正至20和120阶的WG-Stokes函数及VK-Stokes函数,随着积分半径变化的情况;图1(e)为近区,相同修正阶次、不同截断阶次下,VK-Stokes函数随积分半径变化的情况;图1(f)为近区,相同截断阶次、不同修正阶次下,VK-Stokes核函数随积分半径变化的情况。
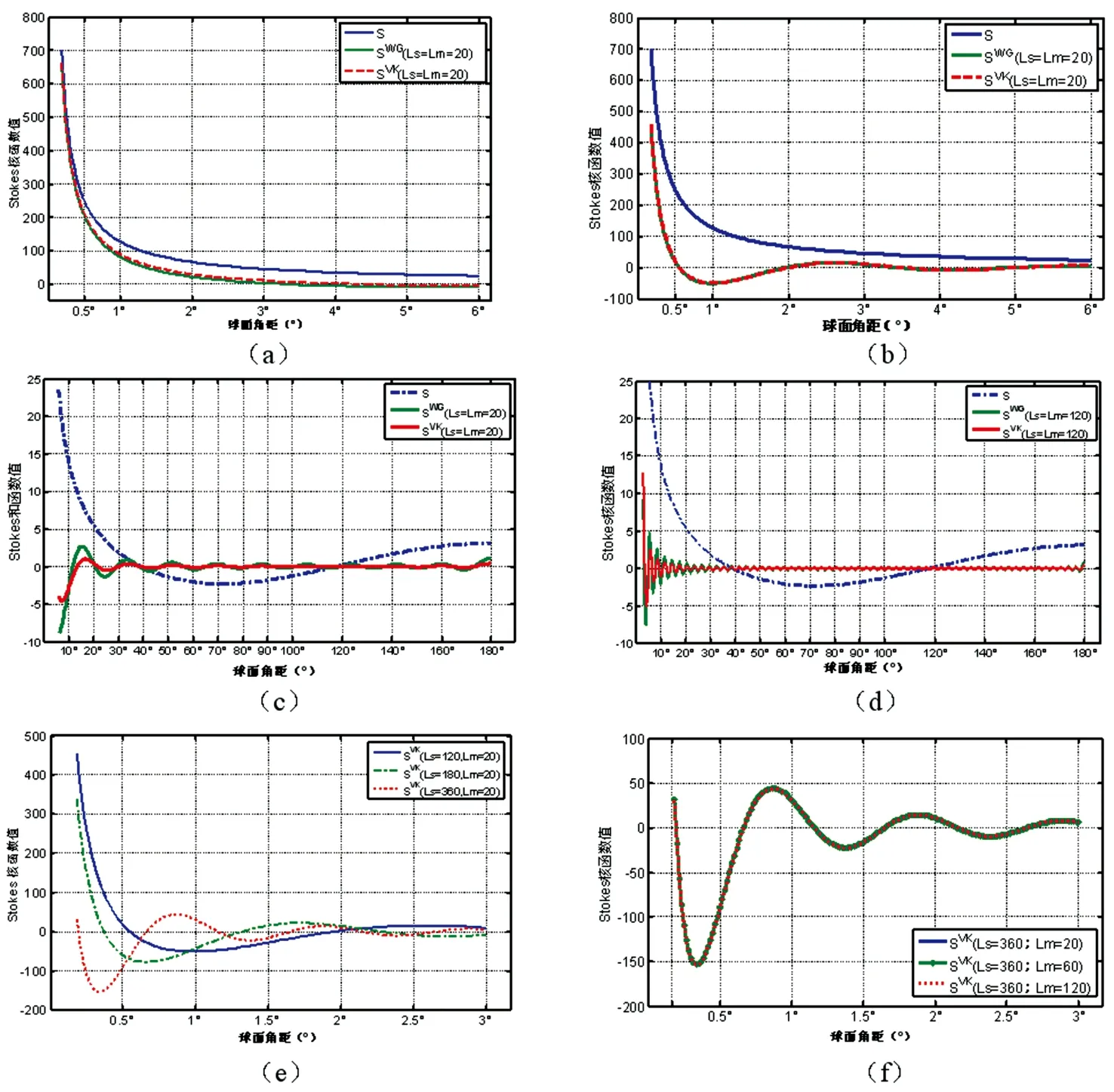
图1 Stokes核函数特性图
由图1(a)和(b)可见,积分半径约在0.2°以内,三函数值最为接近。随着积分半径增加,Stokes核函数与标准Stokes核函数值差异增大。截断阶次越高,VK-Stokes和WG-Stokes收敛速度则越快。VK-Stokes核函数是在WG-Stokes核函数基础上,使得截断上限满足最小,因此与WG-Stokes核函数在近区较为接近。
由图1(c)和(d)可见,远区、VK-Stokes较WG-Stokes收敛快,且比标准Stokes核函数计算值小。由此看来,VK-Stokes核函数能够减弱远区影响。
由图1(e)和(f)可见,截断阶次对VK-Stokes核函数的影响比修正阶次对其影响大。选用较低修正阶次,可提高计算速度。
5.2 截断误差系数分析
基于EGM2008位系数模型,分析截断误差系数与修正阶次、截断阶次以及积分半径的关系。图2(a)和(b)分别为Ls=Lm=20和120阶,不同积分半径(1°、3°和6°)下,VK-Stokes核函数相应的截断误差系数随模型阶次变化图。图2(c)为积分半径6°,Ls=Lm=20,WG-Stokes和VK-Stokes函数相应的截断误差系数随模型阶次变化图。

图2 截断误差系数图
如图2(a)和(b)可见,VK-Stokes核函数截断误差系数受截断阶次影响较大。随着积分半径Ψ0增加,收敛速度加快;但当积分半径超过3°时,其收敛速度减缓。
由图2(c)可知,VK-Stokes核函数截断误差系数比WG-Stokes核函数截断误差系数收敛快。
5.3 截断误差分析
基于EGM2008地球重力场位系数模型,以B=30.72211,L=110.40191,H=1045.3m为例,采用VK-Stokes核函数,选择Ls=Lm=20,积分半径1°和3°,计算远区截断误差,见图3(a)所示;选择Ls=120;Lm=20和Ls=Lm=120,积分半径1°和3°,分别计算远区截断误差,见图3(b)和(c)。

图3 远区截断误差
由图3(a)可见,截断并修正至20阶,其截断误差在几个厘米量级,这对于建立1cm精度大地水准面来说不恰当,还需增大截断阶次或者积分半径来提高计算精度。
由图3(b)和(c)可知,截断至120阶,其截断误差在1cm以内。积分半径对VK-Stokes的截断误差影响较小,因此可选较小积分半径。随着积分半径增加,VK-Stokes核函数作用减弱。在实际截断误差当中,还包括重力测量误差以及地球重力场位系数等误差,这些误差为固定误差。
6 小 结
区域或局部(似)大地水准面精化工作中,常受到数据量稀少的限制,长波以及系统性误差污染,给计算带来不便,影响计算精度。通过修正Stokes核函数,可增强近区计算能力,削弱远区影响,抑制其他污染源影响。
VK-Stokes核函数既可有效利用有限的地面重力测量数据,还能减弱远区影响,但其作用会随着积分范围增大而减缓。从计算效率角度考虑,选用较高截断阶次和较小积分半径更为合适。修正阶次对计算精度影响不大,但其阶次选取影响计算速度,因此可选用较低阶次。
相对而言,VK-Stokes核函数截断误差系数比WG-Stokes和标准Stokes核函数截断误差系数收敛快,且截断误差影响数值也较小,因此选用VK-Stokes核函数相对合理。值得注意的是,本实验只反映了单项截断误差,尚未顾及重力异常观测误差,以及参考模型位系数误差等因素,在实际应用当中还需进一步分析研究。
[1]陆仲连.地球重力场理论与方法[M].北京:解放军出版社,1996.
[2]Hofmann-Wellenhof B. and H. Moritz, Physical geodesy [M].second edition, Springer Wien New York, 2006.
[3]李建成.我国现代高程测定关键技术若干问题的研究及进展[J].武汉大学学报· 信息科学版,2007,32(11):980-987.
[4]李建成.最新中国陆地数字高程基准模型:重力似大地水准面CNGG2011[J].测绘学报,2012,41(5):651-660.
[5]魏子卿,王刚.用地球位模型和GPS /水准数据确定我国大陆似大地水准面[J].测绘学报,2003,32(1):1-5.[6]魏子卿.大地水准面短议[J].地理空间信息,2009,7(1):1-3.
[7]黄谟涛,翟国君,管铮等.海洋重力场测定及其应用[M].北京:测绘出版社,2005.
[8]L.E.Sjöberg,A.Hunegnaw.Some modifications of Stokes formula the account for truncation and potential coefficient errors[J].Journal of Geodesy,2000,74(3):232-238.
[9]L.E.Sjöberg.A computational scheme to model the geoid by the modified Stokes formula without gravity reductions[J].Journal of Geodesy,2003,77(4):423-432.
[10]W.E.Featherstone,J.D.Evans,J.G.Olliver.A Meissl-modified Vanicek and Kleusberg kernel toreduce the truncation error in gravimetric geoidcomputations[J].Journal of Geodesy,1998,72(3):154-160.
[11]P.Vanicek,W.E.Featherstone. Performance of three types of Stokes’s kernel in the combined solution for the geoid[J].Journal of Geodesy,1998,72(9):684-697.
[12]J.D.Evans,W.E. Featherstone.Improved convergence rates for the truncation error in gravimetric geoid determination[J].Journal of Geodesy,2000,74(2):239-248.
[13]A. Ellmann. Two deterministic and three stochastic modifications of Stokes’s formula:a case study for the Baltic countries[J].Journal of Geodesy,2005,79(1):11-23.
[14]W. E. Featherstone, J. F. Kirby, C. Hirt,et al. The AUSGeoid09 model of the Australian Height Datum[J].Journal of Geodesy,2011,85(3):133-150.
[15]Y. M. Wang, J.Saleh, X. Li,et al. The US Gravimetric Geoid of 2009(USGG2009):model development and evaluation[J].Journal of Geodesy,2012,86(3):165-180.
[16]J.Huang,M.Veronneau.Canadian gravimetric geoid model 2010[J].Journal of Geodesy,2013,87(9):771-790.
[17]傅露,褚永海.区域大地水准面确定中Stokes核函数的应用[J].大地测量与地球动力学,2013,33(2):110-113.
Performance Analysis of the VK-Stokes Kernel Function
Rong Min1,2,3,Zhou Wei3,Wu Fumei2,Ren Hongfei2
1. Institute of Geospatial Information,Information Engineering University, Zhengzhou 450052,China 2. Xi’an Research Institute of Survey and Mapping, Xi’an 710054,China 3. Technical Division of Surveying and Mapping,Xi’an 710054,China
In order to get high accuracy of the geoid and to overcome the problem that the gravity data cannot cover the whole world, modified Stokes kernel function is often used to deal with the difficulty. It can improve Stokes kernel function characteristics and make it achieve high accuracy in the small integral range. The characteristics and the far-region truncation error of the VK-Stokes kernel function are analyzed in this paper based on the gravity potential coefficient of the model EGM2008. The results show that in the near-region of the integral radius 0.2°,the VK-Stokes value is close to that of Stokes and WG-Stokes. But with the increasing of integral radius, VK-Stokes converges faster than Stokes and the truncation error of the VK-Stokes kernel function is relatively small in the far-region. Thus it shows the VK-Stokes not only improves the ability of computation in the small integral range, but also controls the truncation error in the far-region.
geoid;Stokes kernel function;VK- Stokes kernel function;truncation error
2015-01-13。
国家自然科学基金资助项目(41174018; 41304022;41474015)。
荣敏(1977—),女,工程师,主要从事重力大地水准面计算方法的研究。
P223
A

