半捷联滚仰导引头视线角速度重构提取技术

孙 高， 赵桂军， 吕鉴倬， 曹培培

（上海无线电设备研究所，上海200090）

0 引言

滚仰式导引头以其独特的极坐标机械结构，实现俯仰框架-90°～+90°与滚转框架0°～360°转动［1］，视场覆盖前半球，满足了未来导弹导引头大离轴角、大探测角的发展需求。

本文从滚仰导引头框架结构与运动形式出发，对比了极坐标和直角坐标之间运动的差异，对由滚转运动引起的视线角速度x 维的旋转进行了视线归零重构，且在半捷联稳定方式下，采用弹体角速度和框架角速度融合的方式，完成了视线角速度y 维和z 维的提取，为滚仰捷联式导引头工程化应用提供了理论分析。

1 滚仰导引头视线角速度x 维旋转问题

滚动俯仰（滚仰式）半捷联导引头框架结构为极坐标形式，与传统框架式导引头的重要区别是其信息的测量和控制量的获得是在不同坐标系下描述的，由于存在描述坐标系不统一的问题，测量给出的视线角速度也不同于传统的框架式导引头。因此，为了分析滚仰式导引头的视线角速度，将滚仰式导引头与传统的偏航俯仰式（偏仰式）导引头进行对比，其坐标关系如图1所示。

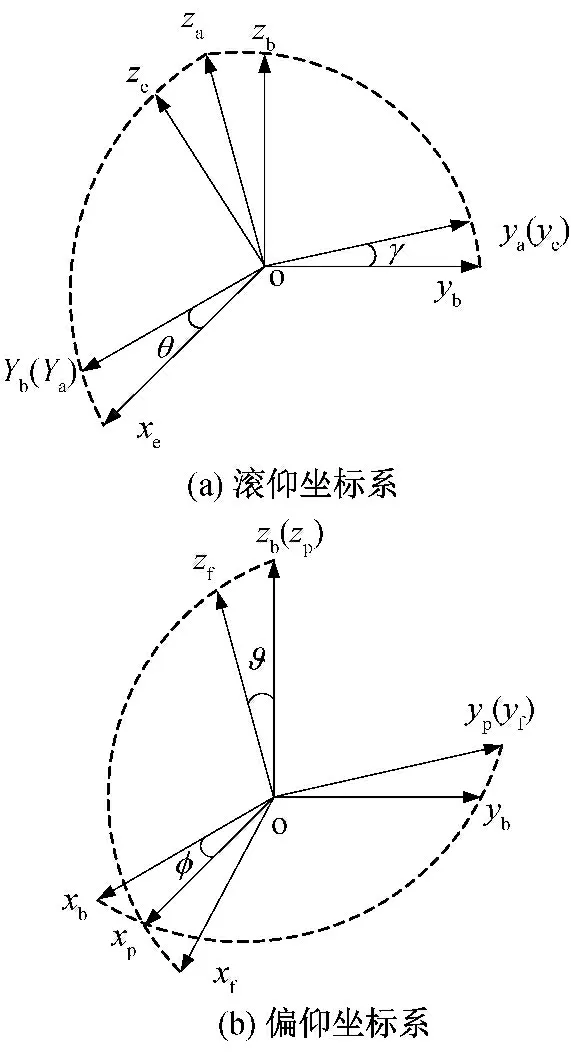
图1 滚仰坐标系与偏仰坐标系

滚仰式导引头坐标系可分为滚转坐标系oxayaza，俯仰坐标系oxeyeze，如图1（a）所示，其中γ为滚转角，θ为俯仰角。偏仰式导引头坐标系可分为偏航坐标系oxpypzp，俯仰坐标系oxfyfzf，如图1（b）所示，其中φ 为偏航角，ϑ为俯仰角。

在导弹跟踪目标的过程中，滚仰式导引头和偏仰式导引头都可以通过执行电机控制平台框架运动，使导引头天线指向目标。根据坐标系之间的相对关系，可以得到滚仰式导引头和偏仰导引头各坐标系之间的姿态变换矩阵，进而可以确定由弹体坐标系到滚仰坐标系的坐标变换矩阵Rb，e和由弹体坐标系到偏仰坐标系的坐标变换矩阵Rb，f分 别 为

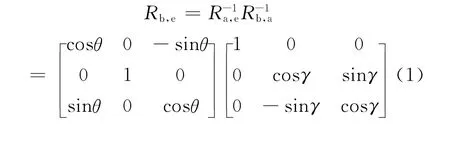
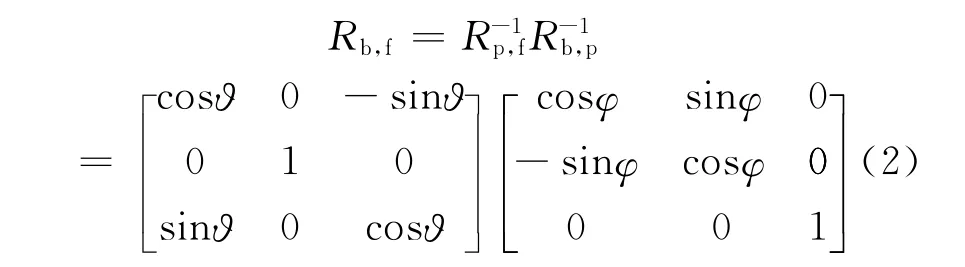
假设弹目视线上的单位向量为R ＝［1 0 0］T，则 可 以 根 据 坐 标 变 换 矩 阵Rb，e和Rb，f得到该向量在弹体坐标系下投影的两种表达方式Rbe和Rbf，如式（3）和式（4）所示。

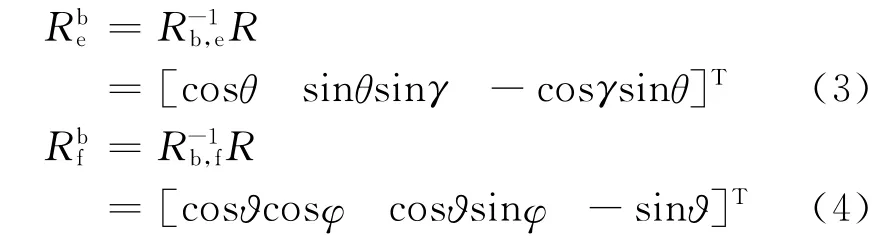
由于导引头指向同一个目标，因此可得

由式（5）可以求得滚仰导引头框架角和偏仰导引头框架角之间的关系为

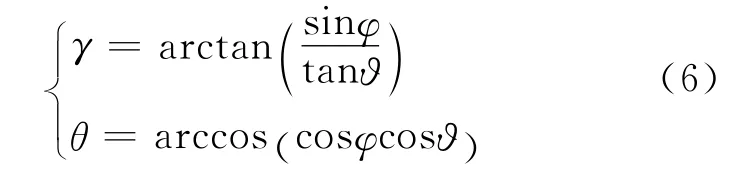
在制导过程中，给出的视线角速度是在惯性坐标系描述的。弹体坐标系到惯性坐标系的转换由弹体姿态的欧拉角决定，为了对比偏仰和滚仰导引头在指向目标过程中的角速度，可将二者投影到弹体坐标系，可得

由式（6）、（7）和（8）可知，当指向同一目标时，偏仰天线角速度和滚仰天线角速度不相等，即≠。

考虑到滚仰导引头和偏仰导引头机械结构的差异性，将偏仰坐标系与滚仰坐标系相对于弹体坐标系的角速度分别投影到各自的天线坐标系，可得

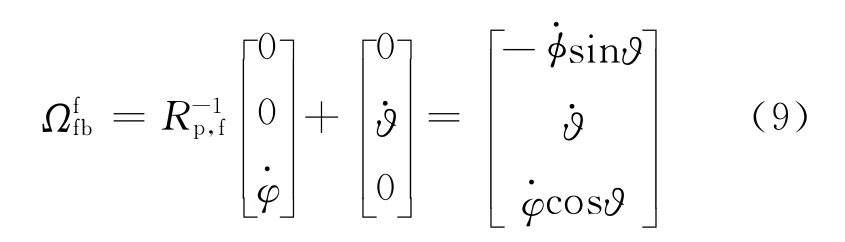
可见，由于偏仰导引头和滚仰导引头的框架结构特性的差异，导致框架运动方式不同，在指向同一目标的过程中，虽然二者在框架角度上有一定的对应关系，但是各自天线坐标系都存在绕x轴的旋转运动，即两天线坐标系的x 轴指向相同，但是y 轴和z 轴却不重合，这导致了视线角速度的不相等。

2 视线角速度x 维归零重构

为了消除滚仰导引头与偏仰导引头角速度的差异，令两个天线坐标系绕自身x 轴旋转的角速度为零，即令

将得到的天线角速度投影到弹体坐标系下，可得

结合式（6）可知

实际中，导弹制导所需的视线角速度为惯性视线系的角速度，为了满足实际制导中视线角速度的需求，必须采用重构的方式提取滚仰导引头x 维的视线角速度。惯性坐标系、视线坐标系和弹体坐标系之间的关系如图2所示，其中oxiyizi为 惯 性 坐 标 系，oxbybzb为 弹 体 坐 标 系，oxlylzl为视线坐标系。

惯性系到视线系的坐标转换矩阵Ri，l可以用惯性系到中间坐标系的转换矩阵Ri，lm和中间坐标系到视线坐标系的转换矩阵Rlm，l表示，采用视线高低角ϑl和视线方位角表示为

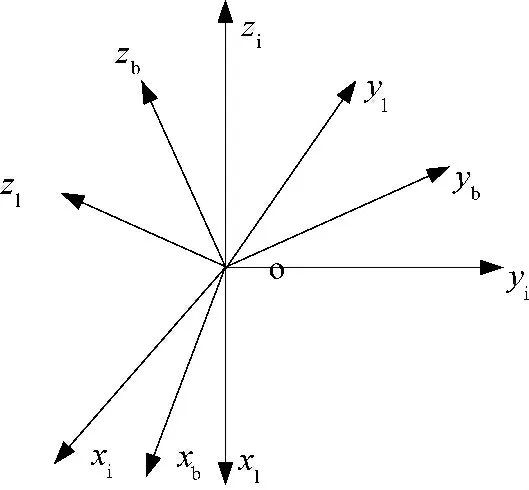
图2 惯性坐标系、视线坐标系和弹体坐标系的关系

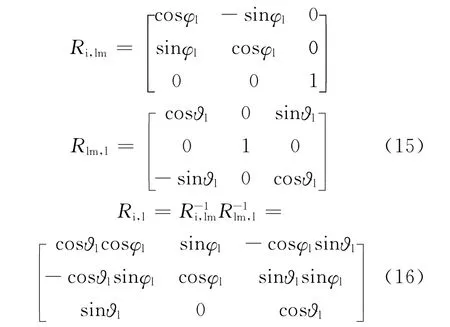
由惯性系到滚仰坐标系的坐标转换矩阵Ri，e可以用弹体姿态角ϑb、ψb、γb和滚仰框架角γ、θ表示，可得

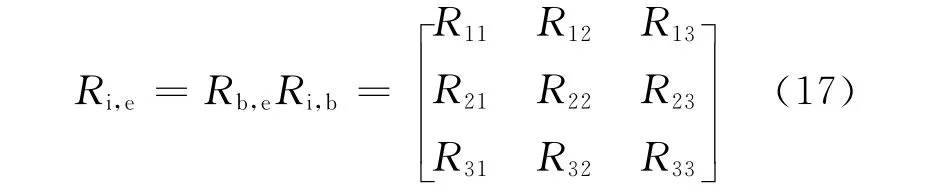
其中：

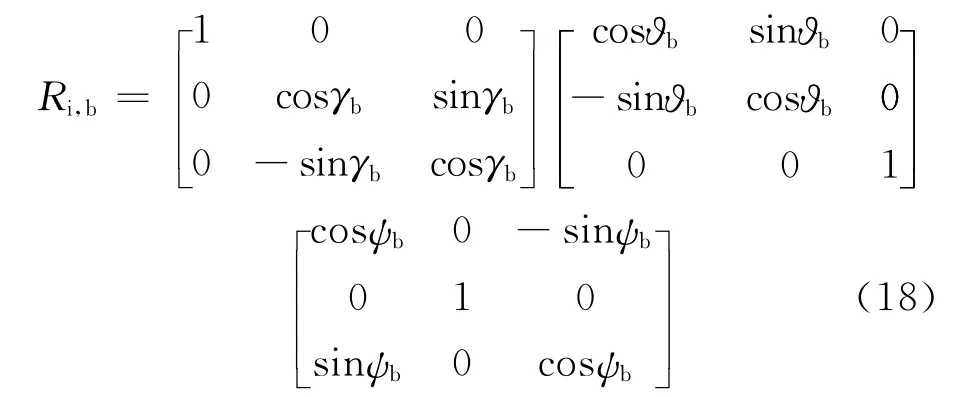
在不考虑跟踪误差时，滚仰坐标系的x 轴与视线系的x 轴重合，都指向同一目标。因此，根据式（5）的推导方式，利用式（16）和式（17）可得

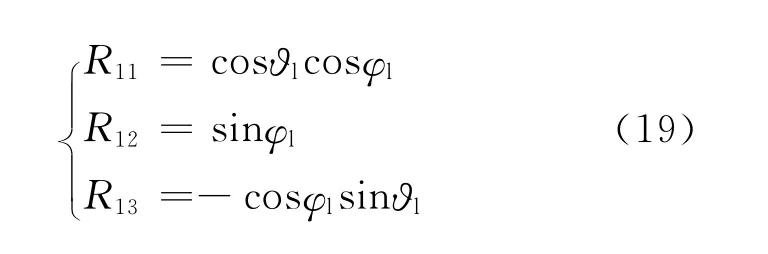
由图2可以看出，视线坐标系是由惯性坐标系先以角速度φ·l 绕ozi轴旋转φl 角度（视线方位角），再以角速度ϑ·l绕中间坐标系oyl轴旋转ϑl角度（视线高低角）得到。因此，视线角速度在中间坐标系oxlm轴上的速度投影为零。

令滚仰坐标系的惯性角速度为Ωe＝［ΩexΩeyΩez］T，则可得

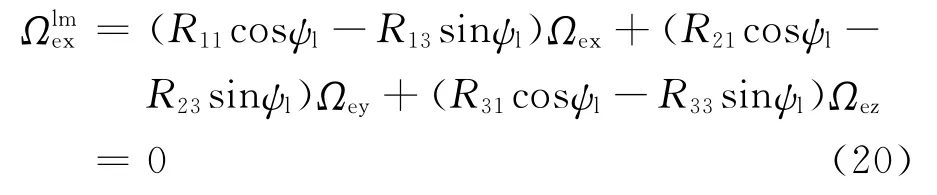
将式（19）代入式（20），求解得

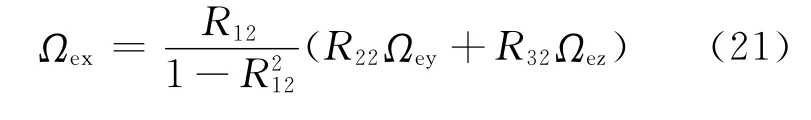
其中：

3 半捷联方式下视线角速度的提取

在完成滚仰导引头惯性视线角速度x 维重构的基础上，必须实现对y 维和z 维的提取。在传统速率陀螺稳定方式下，可在滚仰导引头内框架上安装两轴速率陀螺测量Ωey和Ωez，而在半捷联稳定方式下［3］，框架上没有惯性器件，必须采用信息融合的方法完成视线角速度的提取。

半捷联稳定控制原理如图3所示。因此，半捷联方式下，框架视线惯性角速度是由弹体相对惯性空间角速度和框架相对弹体角速度通过一定的方式融合而成的。

图3 半捷联稳定控制原理

假设弹体相对于惯性空间的角速度为ωb＝［ωbxωbyωbz］T，滚仰坐标系相对于弹体坐标系的框 架 角 速 度 为ωγ＝ ［0 0］T和ωθ＝［00］T。其中，弹体角速度一般可由捷联陀螺或者惯导单元测量得到，而框架角速度可采用微分框架角位置信号的方法获取。根据坐标转换矩阵可知，由弹体运动和框架运动共同引起的滚仰导引头的天线坐标系的角速度为

滚仰导引头y 维和z 维的惯性视线角速度为

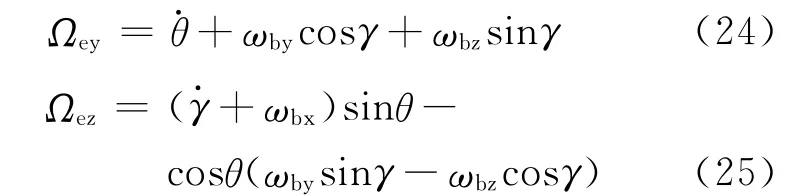
由此，可以得到半捷联稳定方式下，滚仰导引头的惯性视线角速度为

4 结束语

本文从极坐标系和直角坐标系的结构和运动形式出发，分析了滚仰导引头与偏仰导引头视线角速度差异的原因，对x 维视线角速度进行归零重构，消除了滚仰视线角速度x 维的差异。在半捷联稳定方式下，根据半捷联稳定控制原理，结合捷联陀螺测量信息和微分框架角位置信息，采用非线性坐标变换的方法，完成了滚仰导引头y 维和z 维的视线角速度提取。该滚仰导引头视线角速度重构提取技术为工程应用提供了理论依据［4］。

［1］ 王志伟，祁载康，王江.滚仰式导引头跟踪原理［J］.红外与激光工程，2008，37（2）：274-277.

［2］ 陈雨，赵剡，张同贺，等.滚仰式捷联导引头跟踪原理与仿真［J］.航空兵器，2010，（5）：55-58.

［3］ 杨宝庆，徐龙，姚郁.半捷联式导引头视线转率提取算法［J］.北京航空航天大学学报，2011，37（7）：839-843.

［4］ 张靖男，赵兴锋，郑志强，等.战术导弹制导率设计［J］.航空兵器，2006，（3）：3-6.