弹载相控阵自适应低副瓣杂波抑制方法

黄 飞， 周 焯， 郑巧珍

（上海无线电设备研究所，上海200090）

0 引言

雷达导引头在低空巡航或下视尾追目标时，低俯仰角区域杂波（如地／海杂波、多径信号等）进入天线副瓣。此时，若不进行杂波抑制，传统方法将难以从杂波中分离出目标信号，致使目标检测性能大幅下降。抗副瓣杂波干扰最直接的方法是采用低副瓣技术［1-2］。较之常规机扫导引头的固定形状低副瓣，相控阵导引头的副瓣具有灵活可变的优势。早期的相控阵导引头低副瓣技术为全空域低副瓣技术，该技术存在波束展宽明显、天线增益降低等问题。针对上述问题，学者们提出了非对称副瓣技术［3-4］。非对称副瓣技术仅对波束对地副瓣区进行低副瓣处理，通过降低对地副瓣波束电平减小导引头下视尾追时地海杂波的影响。该方法针对整个对地副瓣区域进行低副瓣处理，较之全空域低副瓣技术，区域范围虽有所减少，但该方法依然存在问题：一是，权系数需通过遗传算法及其他优化算法脱机计算后，预存于雷达导引头波控机中，实时性和灵活性较差；二是，针对对地全副瓣区域进行低副瓣处理，低副瓣能力有限。

本文提出一种自适应低副瓣杂波抑制方法，该方法采用增加虚拟杂波干扰源个数及宽杂波零馅的措施，通过构造虚拟接收数据协方差矩阵的方法，自适应在影响目标信号识别的杂波角度特定区域形成宽零馅，使波束形状与战场环境匹配，抑制地面副瓣杂波。该方法中将强地海杂波所处的区域作为虚拟杂波干扰源的来波方向，强杂波干扰所处的大致区域范围可根据预装弹速、目标速度以及弹体下视角获得，或是通过导引头变换低副瓣区域并比较信号处理数据确定。较之非对称副瓣方法，具有更高的灵活性和针对性，强杂波区域副瓣更低，杂波抑制能力更强。且该方法不仅适用于多通道相控阵导引头，亦适用于传统的和差三通道相控阵导引头。

1 信号模型

阵列模型为Nr×Nc的均匀矩形面阵，位于yoz平面，导弹飞行速度v 平行于x 轴，如图1示。以（1，1）阵元为参考坐标点，相邻阵元行列间距分别为d1和d2。φ和θ 分别为来波方向的方位角和俯仰角。平面阵列的第（m，n）个天线阵元在t时刻接收的数据可以表示为

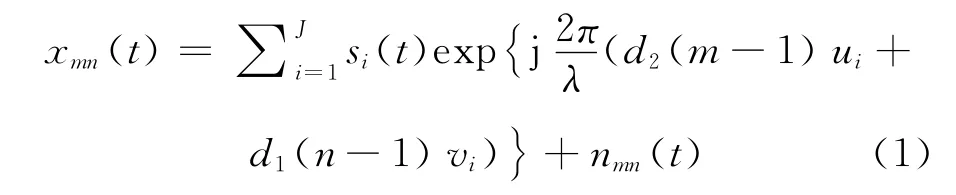
式中：m＝1，2，…，Nr；n＝1，2，…，Nc；si（t）为第i个信号的复包络；ui＝sinθi，vi＝cosθisinφi，θi和φi为第i 个信号来波方向的仰角和方位角；nmn（t）为零均值，方差为β2的高斯噪声。

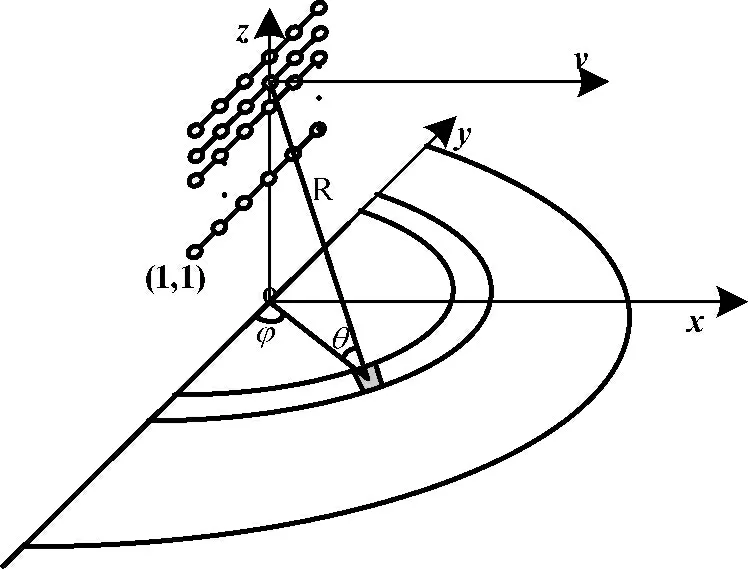
图1 弹载雷达模型图

回波建模仿真首先根据雷达导引头所处战场环境设置状态参数，主要参数：速度、空载平台高度、偏航角、俯仰角、天线方位角、天线俯仰角、天线方向图、脉冲重频、脉冲宽度、发射脉冲峰值功率、环境参数（地面类型、海况）等。按雷达方程及各类回波模型产生对应回波数据。杂波回波数据建模采用相干杂波模型［5］，利用杂波的相位关系，仿真实际雷达导引头的整个信号处理和目标检测过程。地面散射单元的划分方法采用距离环地面散射单元划分方法，每个散射单元对应的天线增益、多普勒频移、距离、入射角、杂波反射率为常数。杂波信号的计算简化为对每个散射单元回波信号的相干叠加。整个雷达照射区域内，把地表分成多个（ΔR／cosθ）×Δφ 的栅格单元。其中：ΔR 为距离环宽度；Δφ 为方位角间隔。一个散射单元作为一个点散射体，根据雷达方程，雷达接收到（θ，φ）处散射单元回波信号幅度可表示为

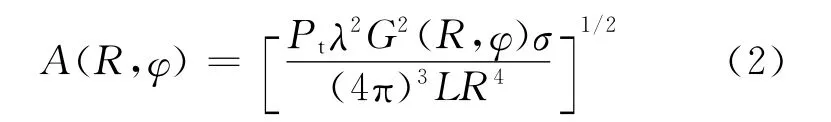
式中：Pt为雷达发射信号峰值功率；λ为雷达工作波长；G（R，φ）为天线在斜距R、方位角φ 处的功率增益；σ为散射单元的回波散射截面积，等于散射面积与后向散射系数的乘积；L 为雷达发射接收综合损耗。

2 自适应低副瓣抗杂波方法

本文提出的弹载相控阵自适应低副瓣抗杂波方法，采用增加虚拟杂波干扰源个数及宽零馅设计，构造虚拟接收数据协方差矩阵，实现自适应宽零馅低副瓣波束形成，在强地海杂波区域形成宽波束零馅抗地海强杂波。该方法不仅适用于多通道相控阵导引头，也适用于传统的和差三通道相控阵道导引头。多通道相控阵雷达导引头可在信号处理机中利用本文方法计算抗杂波低副瓣权重系数，并对各天线子阵接收数据加权低副瓣权重系数实现实时杂波抑制处理。而和差三通道相控阵雷达导引头需将该方法计算得到的低副瓣加权系数从信号处理机传给波控板，由波控板完成各阵元T／R 组件的幅度相位控制即低副瓣加权处理，实现自适应低副瓣波束赋形。

该方法将强地海杂波所处的区域作为虚拟杂波干扰源的来波方向，强杂波干扰所处的大致区域范围可根据预装弹速、目标速度以及弹体下视角获得，或是通过导引头变换低副瓣区域并比较信号处理数据确定。

随着地理信息、数字处理、海量随机访问存储器等技术的迅速发展以及雷达系统本身实时性能的不断提高，使雷达在对本身数据处理前获取更多外界环境的先验知识成为可能。如果雷达系统能够通过与其它传感器系统进行信息共享（如导航系统、电子战系统等机载设备之间的信息共享），了解外界干扰环境的变化情况（如陆海交界处，潜在干扰的位置和参数），或实时地与先验知识数据库进行交互获知地面类型及地面特征，再结合本文的方法可使雷达系统的性能得到提高。利用先验信息提升雷达检测、跟踪和目标识别性能的技术称为知识辅助（Knowledge Aided，KA）技术［6-7］。当与先验知识相结合时，本文的自适应低副瓣杂波抑制方法即属于KA 技术，它是新一代机载／空基预警监视、GMTI雷达、弹载雷达的发展方向。

假设来自强地海杂波区域的P 个杂波干扰源信号入射到阵元数为M，阵元间距为λ／2的均匀线阵上，阵元噪声为空间白噪声，则天线阵列接收信号可表示为

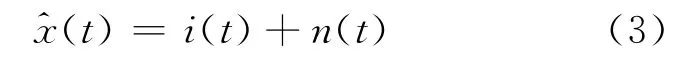
式中：n（t）为噪声；i（t）为杂波干扰信号。在杂波源两两互不相关的情况下，i（t）可表示为P 个杂波源回波的相干叠加，即

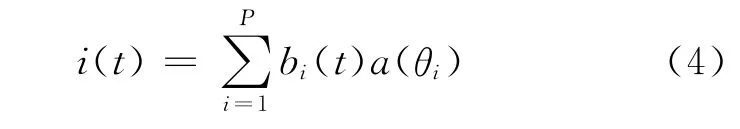
式中：bi（t）为虚拟杂波的复包络；a（θi）为来波方向θi的虚拟杂波的导向矢量。

阵列接收数据协方差矩阵可表示为

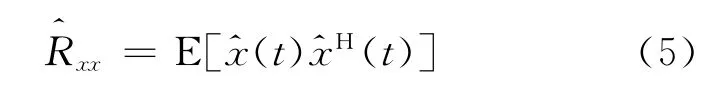
最小方差无失真响应算法（MVDR）是在线性约束最小方差准则下求最优加权值的算法［8-9］。该算法通过最小化阵列输出的功率，来降低干扰和噪声的增益；同时通过对期望信号方向增益附加线形约束的方法，保持波束对期望信号增益不变，从而提高信号干扰噪声比。MVDR 算法的数学模型为

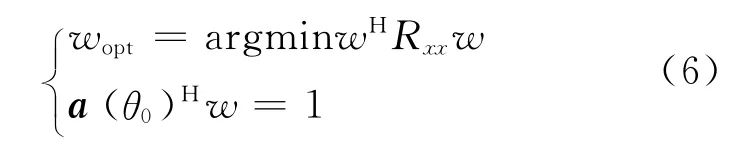
式中：a（θ0）为方向θ0的期望信号导向矢量，即各阵元与参考相位点间相位差矢量；Rxx＝E｛x（t）xH（t）｝为协方差矩阵；x（t）为阵列接收到的信号。最佳权重可表示为

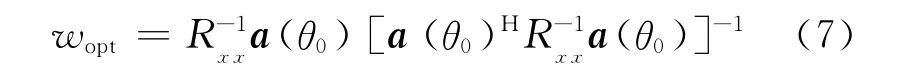
传统MVDR（Minimum Variance Distortionless Response）方法利用平稳过程的各态历经性，通过K 次接收数据快拍数据（采样数据）估计阵列信号相关矩阵Rxx。

在本文的自适应低副瓣方法中，利用式（5）构造的虚拟协方差矩阵代替传统MVDR 方法中利用接收数据估计得到的协方差矩阵。同时采用CMT（Covariance Matrix Tapered）法进行零陷展宽，CMT 基本原理是通过一个锥化矩阵T 对数据协方差矩阵进行扩展［10-11］，即令

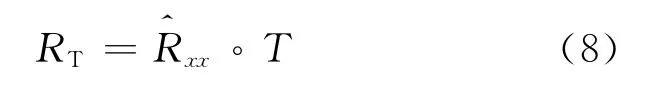
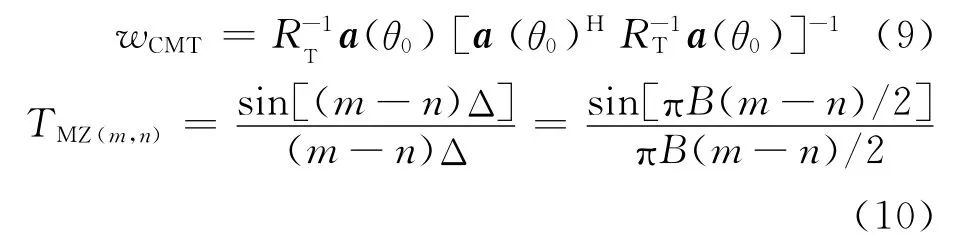
式中：B 为零馅在sinθ的宽度。由式（9）得到的阵列加权系数可在波束方向图的特定旁瓣区域形成宽凹口，有效抑制来自副瓣特定区域的杂波干扰信号。

3 仿真分析

假设某相控阵雷达导引头天线阵采用二维平面阵，阵元数为15×15，行间距和列间距均为λ／2。导引头处于下视尾追状态，主波束波束指向（0，-10°）。导弹飞行方向平行于x 轴，飞行速度为1 500m／s，脉冲重复频率为50kHz。目标出现在（0，-10°），第23 号 距 离 门 处，信 噪 比 为20dB。强杂波回波位于俯仰角-8°～-12°，方位角-11°～-19°，杂噪比为30dB。采用本文的自适应低副瓣杂波抑制方法，设计相控阵雷达导引头天线波束。

图2为自适应低副瓣处理前导引头天线阵列波束在方位俯仰面的投影方向图。图3为自适应低副瓣处理后导引头天线阵列波束在方位俯仰面的投影方向图。

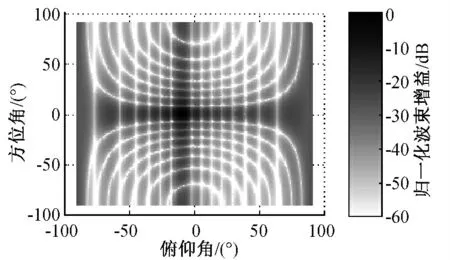
图2 自适应低副瓣前阵列波束方位俯仰面投影方向图

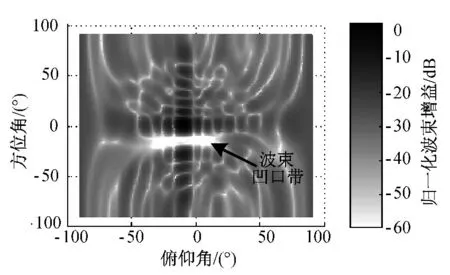
图3 自适应低副瓣后阵列波束方位俯仰面投影方向图

由图3可见，采用本文自适应低副瓣方法后在强杂波区域（俯仰角-8°～-12°，方位角-11°～-19°）形成了较深的零陷，比自适应低副瓣前波束增益下降了30dB以上。图4为自适应低副瓣处理前导引头回波数据，包括目标回波、杂波和噪声信号。

图4 自适应低副瓣处理前导引头回波信号

由图4可见，自适应低副瓣处理前目标回波信号被强杂波信号淹没，无法完成目标检测。图5为自适应低副瓣处理后导引头回波数据。

图5 自适应低副瓣处理后导引头回波信号

由图5可见，采用自适应低副瓣处理后，杂波信号已被有效抑制，可对目标进行检测跟踪处理。

4 结论

针对雷达导引头下视时会受到地海强杂波的干扰，提出一种自适应低副瓣杂波抑制方法，该方法能自适应在影响目标信号识别的副瓣杂波的特定区域形成宽零陷，使波束形状与战场环境匹配，抑制地面副瓣杂波。与非对称副瓣方法相比，该方法具有更高的灵活性、针对性，杂波抑制能力更强。且该方法不仅适用于多通道相控阵导引头，也适用于传统的和差三通道相控阵道导引头。

［1］ 张光义.相控阵雷达原理［M］.长沙：国防工业出版社，2009.

［2］ 潘才军.有源相控阵天线低截获方法研究［D］.成都：电子科技大学，2013：11-20.

［3］ 沈建靓，严继军，玄晓波，等.阵列天线不对称副瓣波束赋形研究［J］.微波学报，2012，（8）：1-3.

［4］ Vince Kluckers.Beam-shaping with Active Phased Array Radars［C］.2008International Conference on Radar，2008：177-187.

［5］ 刘建成，王雪松，施龙飞，等.机载雷达相干杂波模型研究［J］.系统工程与电子技术，2005，27（7）：1222-1225.

［6］ 范曲昆，曲毅.知识辅助机载雷达杂波抑制方法研究进展［J］.电子学报，2012，40（6）：1199-1206.

［7］ Joserph R.Guerci.Congnitive Radar：The Knowledge Aided Fully Adaptive Approach［M］.Artech House，Inc，2010：10-11.

［8］ Capon J.High-resolution Frequency-wavenumber Spectum Analysis［J］.Proceeding of the IEEE，1969，57（8）：1408-1418.

［9］ Peng-cheng Mu，Dan Li，Qin-ye Yin，et al.Robust MVDR Beamforming Based on Covariance Matrix Reconstruction［J］.Science China Information Scinences，2013，56（4）：1-12.

［10］ J R Guerci.Theory and Application of Covariance Matrix Tapers for Robust Adaptive Beamforming［J］.IEEE Trans.on SP，1999，47（4）：977-985.

［11］ 李荣锋，王永良，万山虎.自适应天线方向图干扰零陷加宽方法研究［J］.现代雷达，2003，25（2）：42-45.