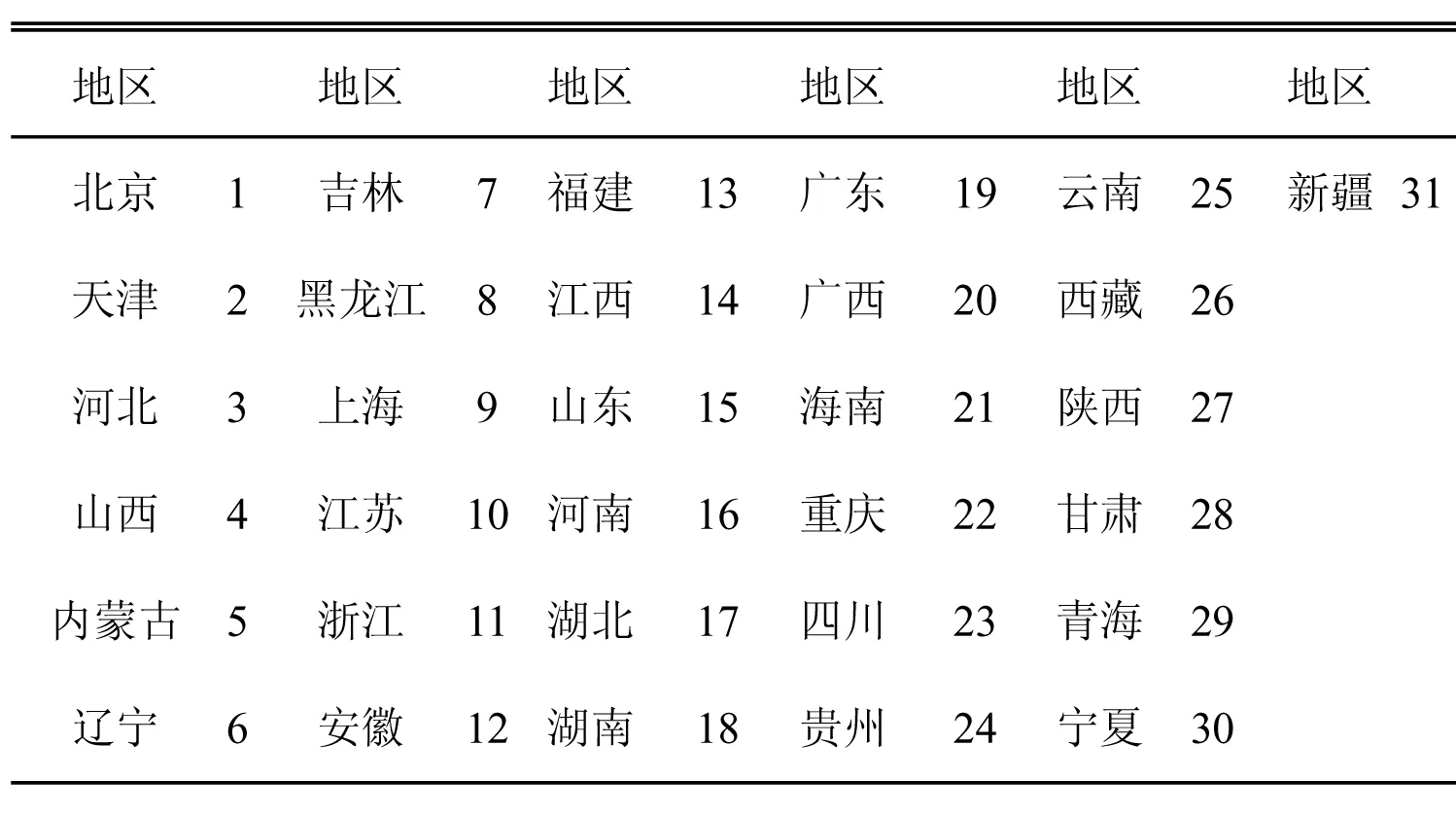
中国省际基本公共服务均等化程度评价研究

朱 洁，李齐云，孔德馨

（山东大学 经济学院，山东 济南 250100）



经济研究

中国省际基本公共服务均等化程度评价研究

朱 洁，李齐云，孔德馨

（山东大学 经济学院，山东 济南 250100）

基本公共服务均等化是当前政府、社会和学界普遍关注的问题。随着中国经济社会的快速发展，公共服务供给不均等的两大表现-总量不足和结构失衡是否得到了改善？本文通过构建评价指标体系，对2001-2011年各省基本公共服务供给水平进行了整体评估。研究发现，供给水平逐年提高，省际间均等化程度有所改善。通过主元分析将观测值分成发展程度较高、中等和较低三类地区。并提出政府要加快职能转变，深化财税体制改革，稳步推进城乡人口基本公共服务全覆盖的政策措施。

基本公共服务；均等化；正义原则；评价指标体系；公共服务指数；财税体制改革

一、引言及文献研究回顾

基本公共服务均等化是当前政府、社会和学界普遍关注的问题。随着中国经济社会的快速发展，公共服务供给不均等的两大表现-总量不足和结构失衡是否得到了改善？很多学者采用不同方法进行分析。

宋文昌（2009）等研究使用公共服务支出所占比重或人均公共服务支出等指标衡量公共服务供给水平，发现分税制改革后，省际间公共服务差距变大。许多研究选取具体服务项目指标，计算公共服务指数和其变异系数①宋文昌：《财政分权、财政支出结构与公共服务不均等的实证分析》，《财政研究》，2009年第3期。。陈昌盛和蔡跃洲（2007）发现公共服务供给总体水平偏低且不平衡，效率低水平趋同②陈昌盛，蔡跃洲：《中国政府公共服务-体制变迁与地区综合评估》，北京：中国社会科学出版社，2007年版。。Zhang和Tang（2013）发现从1996至2006年，省际均等化程度较低，且并未得到改善③Zhang Qi-chun，Tang Xue-bing. Dynamic Evaluation and Determinants of China’s Inter-Regional Equalization of Basic Public Services. Ekonomska istraživanja，2013，26（1）：49-68.。安体富和任强（2012）发现从2000-2010年，省际间基本公共服务水平的差距并没有减小④安体富，任强：《中国省际基本公共服务均等化水平的变化趋势：2000年至2010年》，《财政监督》，2012年第10期。。针对基本公共服务供给现状成因的研究中，吕炜和王伟同（2008）认为地方政府财政能力和城镇化率对公共服务供给有正向效应⑤吕炜，王伟同：《我国基本公共服务提供均等化问题研究——基于公共需求与政府能力视角的分析》，《 财政研究》，2008年第5期。。

综上，现有研究存在三方面的不足：第一，评价方法和高阶指标的合成方式缺少科学规范的分析；第二，指标体系中的满意值、极值等评价参考值的选取主观性较强；第三，构建方法对评价结果和地区排名的潜在影响缺乏分析。本文认为罗尔斯正义原则（Rawls，1999）⑥Rawls J. A Theory of Justice . Harvard university press，1999.与基本公共服务均等化二者存在内在的契合。从这一理论出发，本文拟首先对中国基本公共服务供给水平进行评估。其次，选取基本公共服务指数作为内生变量，通过计量分析探究其成因；最后，通过主元分析，探究数据集结构，对地域进行划分，得出研究结论并提出政策建议。

二、构建基本公共服务评价指标体系

借鉴相关多维度评价指标体系研究（安体富和任强，2012*安体富，任强：《中国省际基本公共服务均等化水平的变化趋势：2000年至2010年》，《财政监督》，2012年第10期。；Human Development Report，2010*Human Development Report. The Real Wealth of Nations: Pathways to Human Development . Palgrave Macmillan，2010.），本文采用综合评价法构建基本公共服务指数。基本思路是选取描述基本公共服务各个维度的单项指标，选定上界和下界将指标原始值标准化，为每个单项指标赋予权重，加总求均值得出维度指数，最后将维度指数加总求和得出整体评估指数。

（一）标准化极值的选择

本研究使用极值法对单项指标原始值进行线性转化，如式（1）所示，目的有二：一是去除单项指标的单位，将其转化为统一量度形式，使其具有可比性；二是通过对原始值的转化，建立[0,1]的变化区间。

（1）

其中，I（x,mx,Mx）和x分别代表指标的标准化值和观测值，Mx和mx是用于缩放的上界和下界。边界值的使用可以量化该地区服务水平与“最低标准”和“最高水平”之间的差距，但也带来了隐患：标准化值的大小和排序对边界值的变化极为敏感（Kovacevic，2010）*Kovacevic M. Review of HDI Critiques and Potential Improvements. Human Development Research Paper，2010，（33）.。为保证合成指数具有可比性，固定值和时间序列数据中的极值都是边界值可行的选择。上界可以理解为基本公共服务供给的理想水平，由于缺少足够的案例研究为服务项目赋予固定阙值，因此选择观测值中的最大值作为上界。所有指标的下界设定为0，表示在极端特殊的情况下，比如战争爆发或极端灾难发生时，地方政府失去提供公共服务的能力（Hobbes，2002）*Hobbes T. Leviathan . Peterborough，2002.。标准化公式调整为：

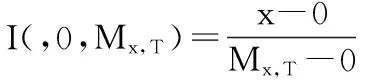
（2）

其中，x是指标的原始值，Mx,T是时间序列中指标x的最大值。边界值下界为0。通过改变边界值，检验了标准化值对边界值变化的敏感性，发现上界的变化只影响指标值的大小，而改变下界则对指标值大小和排序都有影响。公式（2）可以理解为占最大值的比重，即Herrero 等（2010）*Herrero C, Martínez R, Villar A. Multidimensional Social Evaluation: An Application to the Measurement of Human Development. Review of Income and Wealth, 2010, 56（3）: 483-497.推荐的形式，这一方法操作简单，既不影响指数排序和观测值之间的相对估值关系，也不影响相关边际替代比率，可从另一个角度提供有力佐证。

（二）指标权重的赋予

如何为子指标赋予权重是一个棘手的难题，理想的权重代表了各组成部分对于最终结果的影响或贡献。本研究中赋予权重的依据是每项公共服务对于居民生活幸福程度的贡献。理论上说，基本公共服务指数的权重赋予方案可以从个人偏好的视角来决定，通过社会调研和统计分析来获得。HDI研究中有类似的社会调研尝试，Chowdhury等（2006）邀请学者为HDI的组成指标打分（0-10），但最终得出的赋权方案和权重均等模式并无显著不同*Chowdhury S, Squire L. Setting Weights for Aggregate Indices: An Application to the Commitment to Development Index and Human Development Index . Journal of Development Studies, 2006, 42（5）: 761-771.。在实践中，权重均等方案是基于所有公共服务对于个人均等重要的前提，同样也难找到一个先验原理支持赋予某项指标比其他指标更高的权重（Ul Haq，1996）*Ul Haq M. Reflections on Human Development . Oxford University Press, 1996.。总而言之，均等的赋权方案理论上不够完美，但实践上较为可行。

（三）加总公式的选择

算术平均数求和公式（3）广泛用于加总维度指标。

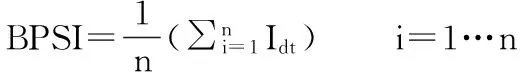
（3）

其中，Idt代表维度i的指数，假定维度总数为n。这一加总公式虽然简单直观，但是存在三个问题：第一，缺少理论上的论证支撑。第二，应用该公式的前提是假定各维度之间具有完全可替代性，存在较大争议。第三，采用加法合成函数得出的指数排序对于单项指标标准化非常敏感。

本文借鉴Chakravarty（2011）*Chakravarty, S.R. A Reconsideration of the Tradeoffs in the New Human Development Index. Journal of Economic Inequality，2011，（9）: 471-474.和Herrero等（2010），采用公理化方法推导加总公式。假设辖区内有n个居民，N={1,2,…,n}。存在基本公共服务项目集合M={1,2,…,m}需要评估。该辖区的公共服务状态定义为一个n排、m列的矩阵X，元素xij表示居民消费的公共服务项目j的评估值。每个服务项目的评估值均已进行了标准化，在区间[0,1]内变动。所有可容许的公共服务状态矩阵的空间可定义为Ω=[0,1]nm。极值矩阵X0和X*分别是由0和1组成的两个特例。xj是矩阵X的第j列，代表第j列对应的公共服务维度对辖区所有人的贡献。定义向量0n（j）和1n（j）分别代表矩阵X0和X*的第j列。去除矩阵X第j列的xj，可以得到一个n×（m-1）阶的矩阵X-j。将这两部分组合得到X=（X-j,Xj）。下面给出公共服务评价指数的定义：

公共服务评价指数是一个连续单值的映射：I:Ω→R，为公共服务项目提供实数形式的评估，其中Ω是[0,1]的k重笛卡尔乘积，R是实数线。

下面给出公共服务评价指数相互独立的5个特性。

1.单调性：对于任意X，X′∈Ω，如果xij>xij′对于所有的i∈N和j∈M都成立，那么I（X）>I（X′）。即当居民消费的基本公共服务的水平提高时，评估值也会随之提高。

2.对称性：对于任意X∈Ω，对矩阵X的列进行任意排列，I（X）保持不变。即所有公共服务维度同等重要。

3.成比例性：令X（α）=α[1n（1）,…,1n（m）]，对于任意α∈[0,1]，I（X（α））=α。当公共服务的供给水平都一致时，指数值相同。

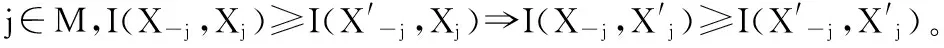
给定基本公共服务评价指数满足上述5条公理和公共服务状态矩阵X，定义一个等值ε（Xj）∈R，与矩阵X的第j列的分布相一致。ε（Xj）独立于X-j，表示如下：

I（X）=I（X-j,1n（j）ε（Xj））

（4）

可得出以下定理：

定理：公共服务评价指数I（*）满足单调性、对称性、成比例性、下界性和可分性，当且仅当指数形式为I（X）=∏j∈M（ε（Xj））1/m,ε（Xj）是Xj的等值*证明过程略。。

令参数a>0，b>0，里昂惕夫加总函数If=min（axE,bxM），由曲线If表示，具有完全互补性。提高合成指数的唯一途径是同时提高所有维度指标。

几何平均数Ig=（xE×xM）1/2对应的等服务曲线处于二者之间，说明Ig具有互补性和替代性。实际上，同时具有一定的替代性和互补性是合理的。一方面，可以通过提高某一个公共服务维度的水平以弥补表现相对较差的服务维度。另一方面，居民需要至少享有最低标准的某些服务，才能有机会享受其他公共服务。如果居民因没有医疗服务而生病致死，那么即使能获得教育也是毫无意义的。

使用几何平均数加总公式的前提下，指标标准化受边界值影响较小。如果对任一子指标，比如，乘以标量参数，如式（5）所示：

Ig=（γxE×xM）1/2=γ1/2（xE×xM）1/2

（5）

这等同于对原式乘以同一个标量，不会影响结果的排序。如果使用算术平均数公式（6），标量的变化会影响子指标的相对权重。

（6）

三、对我国2001-2011年公共服务数据的分析

（一）指标体系的基本架构

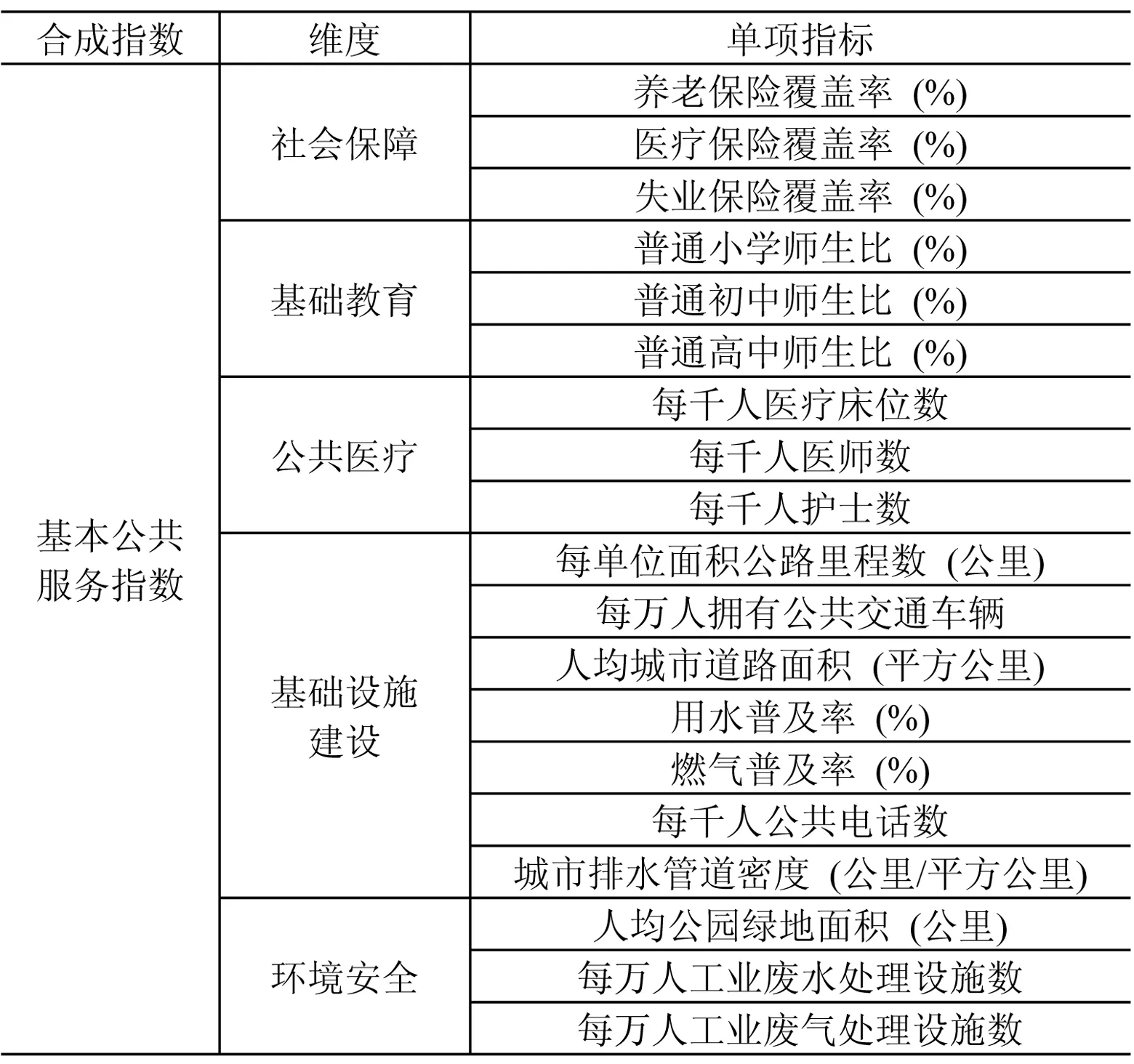
本文从5个方面评估基本公共服务供给的总体水平，包括：社会保障、基础教育、公共医疗、基础设施建设和环境安全。基本公共服务均等化旨在保障所有公民都有平等享有公共服务的途径，也就是追求机会自由（Sen，2002）*Sen, A. Rationality and Freedom . Harvard University Press, Cambridge，2002.。本文从产出的角度选择单项指标以评估服务可获得性和供给水平，构建了包括3个层级、5个维度、19个单项指标的基本公共服务评价指标体系，如表1所示。

表1 基本公共服务评价指标体系

（二）评估结果

计算基本公共服务指数（BPSI）包括两个步骤。第一步，生成维度指数。选定最大值作为对应指标的上界，对单项指标进行标准化，公式如下：

（7）

其中，Is代表单项指标的标准化值，x和max（x）分别是实际值和最大值。

计算维度内单项指标值的几何平均数，即维度指数，公式如下：

（8）

其中，Id代表维度指数，维度中单项指标总数为m。

选取各维度指数最大值作为上界，对维度指数Id进行标准化。

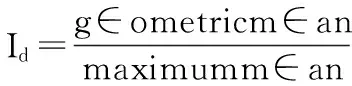
（9）

第二步，将维度指标加总求几何平均数，得出基本公共服务指数（BPSI）。

（10）

其中，Id代表维度指标，共有n个服务维度。

我国2001-2011年31个省份的基本公共服务指数如表2所示。

表2 各地区基本公共服务指数

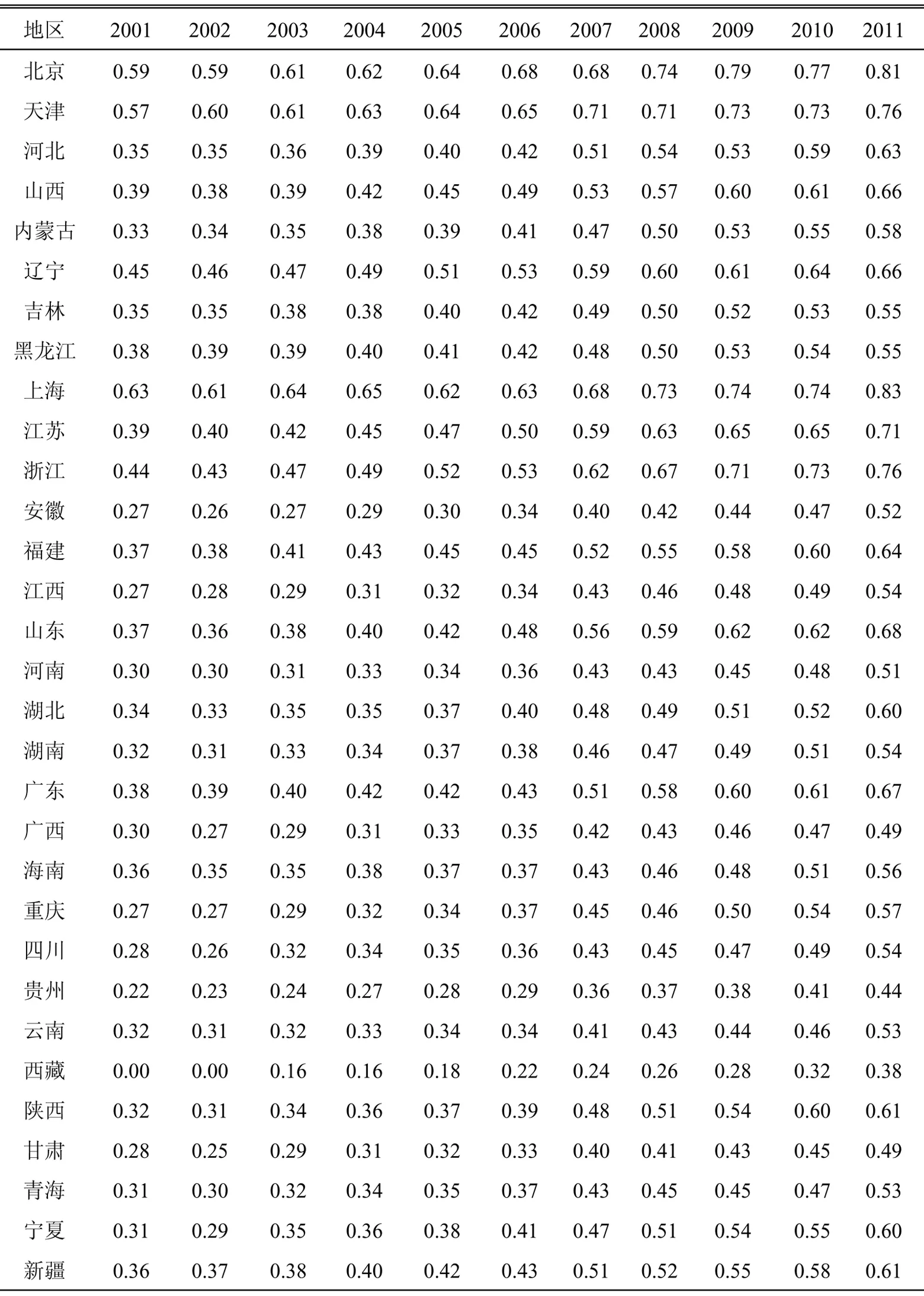
数据来源：根据《中国统计年鉴2002-2012》、《中国劳动统计年鉴2002-2012》、《中国卫生统计年鉴2008-2012》、《中国教育统计年鉴2002-2004》整理计算得出

表3列出了基本公共服务指数的概要统计量。均值逐年增加，说明基本公共服务总体供给水平在逐年提高。变异系数总体上呈下降趋势，说明省际基本公共服务供给水平的均等化程度提高了。

表3 基本公共服务指数的概要统计量

四、基本公共服务指数的决定因素

（一）模型设定与变量描述

为分析基本公共服务指数的决定因素，对2001-2011年31个省份的数据进行分析，构建计量模型如式（11）所示:

bpsii,t=α0+α1deni,t+α2gdpi,t+α3expi,t+α4cdri,t+α6unei,t+α7dpc1t+α8dpc2t+α9dpc3t+α10dpc4t+εi,t

（11）

其中，i和t分别代表地区i和年份t。内生变量bpsii,t表示i地区t年基本公共服务指数。den表示每平方公里人口数，即地区人口密度；gdp表示人均GDP（千元），即地区经济发展水平；exp表示人均财政支出（千元），即地方政府财政能力；upr表示城镇人口比重，即城镇化率；cdr为儿童抚养比；une为失业率。为检验国民经济和社会发展五年规划纲要对公共服务供给的影响，本文设定了4个虚拟变量dpc1，dpc2，dpc3，dpc4，将对应年份的变量设为1，其余年份设为0，分别用于测度规划颁布后第1年至第4年的影响。数据来源为历年《中国统计年鉴》。

（二）实证研究方法

使用White Test检验模型的异方差性。由于使用了地区性特征变量，加之地区间可能存在某些未观测到的和遗漏的异质性，计量模型可能会与个体效应有关。因此使用三种检验：Fisher Test检验混合OLS回归估计量（H0）和个体固定效应估计量（H1），Breush Pagan Test比较混合OLS回归估计量（H0）和随机效应估计量（H1），以及Hausman Test比较个体随机效应（H0）和个体固定效应（H1）。检验结果如表4所示，使用稳健标准差的个体固定效应模型较为合适。

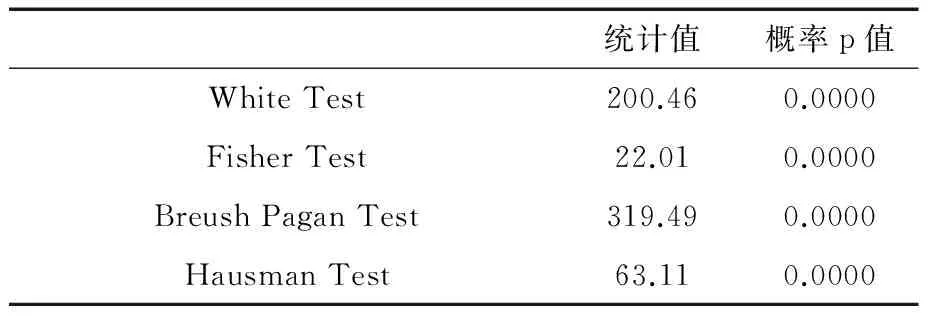
表4 检验结果

（三）计量分析结果

计量回归结果如表5所示，重点关注个体固定效应估计量，模型拟合程度较高，拟合优度为0.89。变量den高度显著并和被解释变量负相关，人口密度每增加一单位会导致公共服务指数下降0.0002个单位。原因是公共医疗服务和教育等俱乐部产品在消费上具有一定程度的竞争性，会随着人口密度的增大导致个人消费比例的减少。变量gdp代表地方经济发展水平，是高度显著且对公共服务指数有正向作用，每增加1单位会导致服务指数上升0.0039个单位。变量exp代表地方政府的财政能力，高度显著且和被解释变量正相关，每增加1单位会导致公共服务指数增加0.008个单位。

表5 计量分析结果

注：括号中是稳健标准差。***、**、*分别表示在1%、5%和10%水平上显著

城镇化率每提高1单位会导致公共服务指数提高0.0051个单位。造成这一现象的原因可能有两点：一方面，现行的公共政策倾向于向城镇人口提供更多的基本公共服务，因此城镇人口比例越高，基本公共服务的总体水平也会越高；另一方面，出于数据可得性的考虑，评价体系中选取的城镇指标相对较多。儿童抚养比对基本公共指数有负向作用，每提高一单位会导致指数下降0.0032个单位。家庭儿童较多会对某些特定的公共服务产生较大的需求，但在我国实行计划生育政策的现状下，高儿童抚养比一般出现在落后地区。除虚拟变量dpc4之外，其他虚拟变量都是显著的，且对基本公共服务指数有正向作用。说明五年规划纲要引领促进了基本公共服务供给水平的提高。其中变量dpc2的系数最大，说明在发展规划颁布后的第二年公共服务水平改善程度最大。

五、评估地区的结构划分

（一）主元分析的数据描述

本文使用主元分析法对评估地区进行结构划分，该方法可以有效地降低数据维度和分析复杂数据集的结构，对观测值进行分类（Le Maux等，2011）*Le Maux B, Minardy F, Magalhaes C. Determinants of Electoral Outcomes: A Simple Test of Meltzer and Richard's Hypothesis. Condorcet Center for political Economy, 2011.，选择我国2001-2011年的面板数据进行主元分析，并额外选取了若干地区特征向量，数据描述和概要统计量见表6。

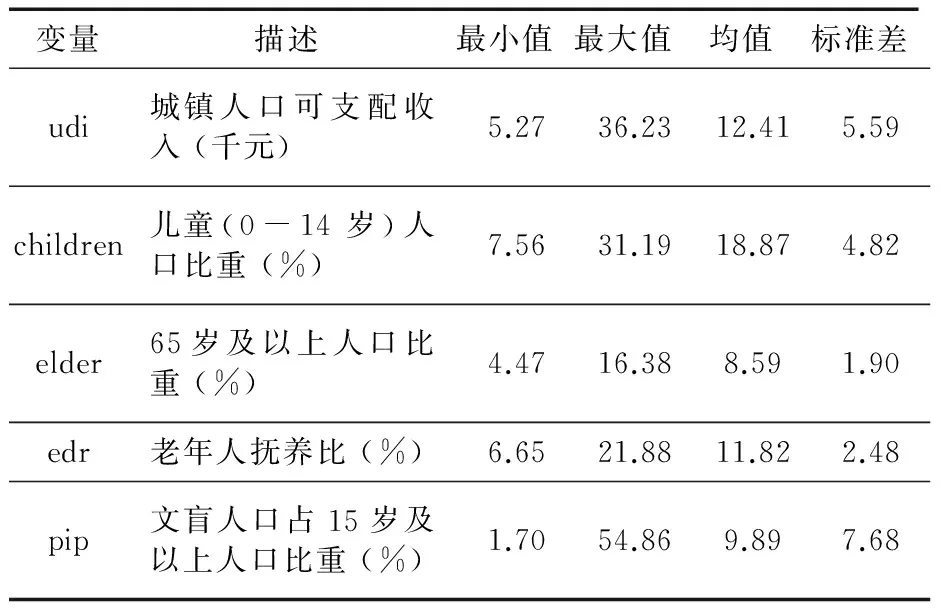
表6 主元分析使用的额外变量概要统计量

数据来源：根据《中国统计年鉴2002-2012》整理计算得出

（二）主元分析结果

主元分析的结果如图1所示，图中描绘了12个变量的相对位置，并与其对应省份保持一致。图中的数字为31个省份的编号，和表7中的设定一致。

表7 主元分析中省份的序号

主元分析结果区分力较强，主要表现在两方面：一是观测值分布的离散性较大，并未集中在坐标系的中央，横轴方向上的排列尤其分散；二是表8中的统计数据说明前两个主分量解释了总方差的72.23%。因此，易于解释主元分析的结果图示，并对数据集进行分类。

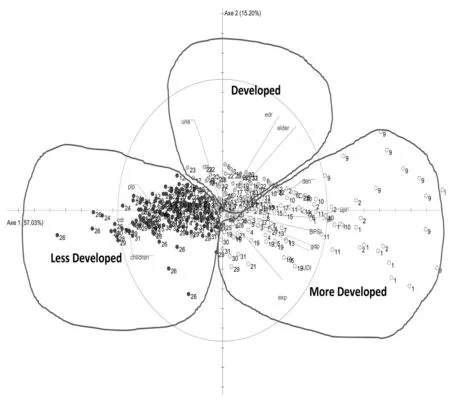
图1 主元分析的结果图示

表8 解释变量的主元分析结果

表8给出了主元分析中变量的正向和负向效应值。对于第一个主分量（横轴），存在一对（1）高人均GDP、高城镇化率与（2）高儿童人口比、高儿童抚养比的对立关系。而第二个主分量（纵轴）由（1）较高的老年人比重和（2）高人均财政支出构成。基于这两种对立关系可以将观测值分为两类：发展程度较高的地区，位于东南象限；发展程度相对不高的地区，位于西北象限。根据人口密度的不同，西北象限的观测值又可以分成两组：一是发展程度中等的地区，人口密度较大、老年人口比重高；二是发展程度较低的地区，儿童抚养比高。具体特征如下：

1.发展程度较高的地区：基本公共服务指数均值最高，达到0.60。人口密度均值和城镇化率都是最高。该区域的经济发展水平较高，人均GDP均值为3.8万元，人均财政支出均值达6380元。该区域还有以下特征：较高的人均城镇人口可支配收入，老年人口比重较高，低失业率，儿童抚养比和老年人抚养比相对较低。主要位于我国东部区域，比如北京（1）和上海（9）。

2.发展程度中等的地区：基本公共服务指数均值为0.44。人均GDP均值为1.69万元。人均财政支出均值最低，只有2580元，这和该区域较高的人口密度有关。老年人口比重和老年人抚养比为三组最高。主要分布在我国东北和中部地域，包括辽宁（6）和重庆（22）等。

3.发展程度较低的地区：基本公共服务指数均值最低，只有0.35。人口密度最低。人均GDP只有1.03万元，城镇人口人均可支配收入最低，只有8750元。儿童人口比重和儿童抚养比较高。主要地处我国西部地域，包括贵州（24）和西藏（26）等。

六、研究结论与政策建议

（一）研究结论

为评估我国基本公共服务供给水平和省际均等化程度，本文构建了多维度指标体系，对5个方面的公共服务进行了总体评价。研究表明，2001-2011年各地区基本公共服务的供给水平不断提高，省际均等化程度总体上得到了改善。

主元分析对各省份的结构划分较为清晰，可分为发展程度较高的地区，主要在东部地域；发展程度中等的地区，主要位于中部和东北地域；发展程度较低的地区，主要位于西部地域。实证分析发现，地方经济发展水平和政府财政能力是公共服务水平提高的基础，城镇化率和国家发展规划对公共服务水平的改善都有较强的正向效应。

（二）政策建议

地方政府的发展规划和支出行为偏好影响着公共服务的供给水平。应当纠正单纯以经济增长速度评定政绩的偏向，加快政府职能转变，加强地方政府公共服务、社会管理、环境保护等职责，加强各类公共服务提供。对于事务性管理服务，可以引入竞争机制，通过合同、委托等方式加大购买公共服务力度。

公共服务地区间不均等程度的改善，内靠本地区经济实力的增强，外靠中央财政再分配政策。要深化财税体制改革，建立事权和支出责任相适应的制度。对于区域性公共服务，中央和地方按照事权划分相应承担和分担支出责任，中央可通过安排转移支付将部分事权支出责任委托地方承担。对于跨区域且对其他地区影响较大的公共服务，中央通过转移支付承担一部分地方事权支出责任。

在城镇化过程中，公共服务供给总体上有所提高，要推进以人为核心的城镇化，同时统筹城乡发展，优先考虑制度覆盖城乡全体居民，再逐步提高统筹层次和保障水平。要加强农民工职业培训和保障随迁子女义务教育，把进城落户农民完全纳入城镇住房和社会保障体系，稳步推进城镇基本公共服务常住人口全覆盖。

[责任编辑：王成利]

国家社会科学基金重大项目“深化收入分配制度改革的财税机制与制度研究”（13&ZD031）；国家社科基金重点项目“深化税收制度改革与完善地方税体系研究”（项目编码：14AZD023）；国家社会科学基金项目“深化税收体制改革研究”（13BJY155）；山东省社会科学基金项目“人口流动背景下的均等化财政转移支付制度研究”（12BJJJ04）。

朱洁（1987—），男，山东大学经济学院博士研究生；李齐云（1955—），男，山东大学经济学院教授，博士生导师；孔德馨（1988—），男，山东大学经济学院硕士研究生。

F202

A

1003-8353（2015）07-0112-06